利用位移图线巧解相遇难题

顾成纲

(上虞市城南中学 浙江 绍兴 312300)

何海明

(绍兴市第一中学 浙江 绍兴 312000)

相遇问题一般涉及两个甚至多个对象，利用图像分析容易找到各运动量间的关系.我们知道速度-时间图线的交点并非是运动质点相遇，但在同一坐标系下质点位移-时间图线交点意义为质点相遇时刻.位移图线的这一直观性给解决相遇问题提供了其独特的优势.下面介绍几种利用位移图线解繁难相遇问题的几种方法.

1 参照系变换法

【例1】某人划船逆流而上.经过桥洞时，船上竹制渔竿不慎掉到河里，小船一直逆行到上游某处才发现，发现后便立即掉头追赶，当他返航t=10 min追上竹竿，此时渔竿距桥洞x=1×103m，若此人划行速率始终不变，不计小船调头时间，试求河水的流速.

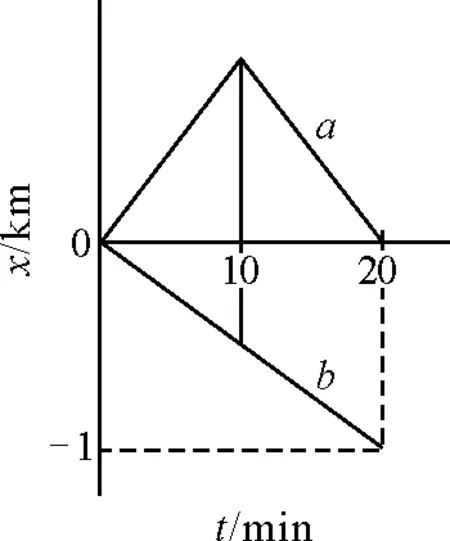
图1

解析：取小船逆流而上划行方向为正方向，以桥为参照并作为位移原点，画出流水的位移图线b.以流水为参照，画出小船的位移图线a.因为小船在流水中往返取物相对流水速率不变，位移图线对称，如图1所示.追及渔杆时，渔杆在流水中已漂流了20 min时间.所以，流水速度为

2 曲直转换法

【例2】甲、乙两球从同一地点做竖直上抛运动，甲的初速度为2v0，乙的初速度为v0，试求乙比甲推迟多久抛出，两球才能在空中相遇.

解析：抛体运动的位移-时间图线是抛物线，如果我们设法消去重力加速度引起的影响，位移图线由曲线变为直线.以自由落体运动物体做参照物就可实现曲直转换.因为抛体运动上升时间和下降时间相等，将返回阶段的位移图线折回到时间轴t，更能反映出抛体运动的对称特点，使问题变得更加直观.画出甲、乙两球相遇的两种临界情况(图2).由图2可直观看出，要使两球空中相遇，乙球比甲球推迟抛出时间范围

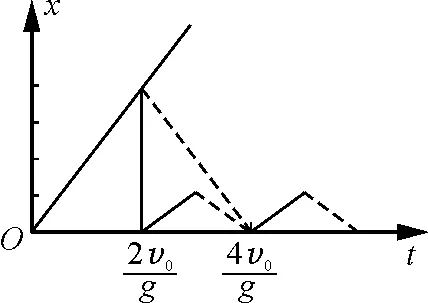
图2

【例3】一个小孩仰躺在地上，手持玩具手枪竖直向上，朝天连续开枪，子弹射出枪口的速度为30 m/s，每隔1 s发射一颗子弹，假设发射的子弹在空中不发生碰撞.试问：对于第一颗子弹，在空中可遇到多少颗子弹从它旁边擦过(不计空气阻力，g取10 m/s2)？

解析：因为重力加速度对每一颗子弹都一样，不考虑自由落体运动的影响，子弹做匀速上升运动.现仍用例题2的策略，将下降过程的图线折回到时间轴一边，每颗子弹的位移图线变成依次错位1 s的等腰三角形(图3)，图线的交点表示两子弹相遇，共有5颗子弹在空中与第一颗子弹相遇.进一步考查图线可以看出，第6颗及其后发射的子弹，在空中10颗子弹都能遇到.

图3

3 虚实转换法

【例4】在一条笔直的公路上，依次设置3盏交通信号灯L1，L2和L3，L2和L1相距80 m，L3和L1相距120 m.每盏信号灯显示绿色的时间都是20 s，显示红色的时间都是40 s.L1与L3同时显示绿色.L2则在L1显示红色经历了10 s时开始显示绿色(信号灯随时间变化的图像如图4所示)，规定车辆到达信号灯时，信号灯显示绿色才能通过，通过3盏信号灯经历的时间不得超过150 s.若一辆匀速向前行驶的自行车通过L1的时刻时L1已显示绿色10 s的时刻，则此自行车能不停顿地通过3盏信号灯的最小速度和最大速度分别是多少？

图4

解析：如果把红绿灯当作路口定时开启、关闭的栅栏，车辆过路口变为了实实在在的相遇问题.画坐标，纵轴为位移，横轴为时间.以信号灯L1绿灯刚亮时刻为零时刻，把三个信号灯的信号图转化为位移图像.在x1=0，x2=80 m，x3=120 m，处分别作三灯L1,L2,L3位移线，实线为绿灯状态，虚线为红灯状态(图5).根据题意，从10 s起作自行车的位移图线，要同时交两信号灯的实线段，经历时间又不得超过150 s，得到符合题意的两条图线，如图5所示.

由图得

【例5】图6(a)是在高速公路上用超声波测速仪测量车速的示意图，测速仪器发出并接收超声波脉冲信号，根据发出和接收到的信号间的时间差，测出被测物体的速度.图6(b)中P1,P2是测速仪器发出的超声波信号，n1,n2分别是P1,P2由汽车反射回来的信号.设测速仪匀速扫描，P1,P2之间的时间间隔Δt=1.0 s，超声波在空气中传播的速度是v声=340 m/s，若汽车是匀速行驶的，则根据图6(b)可知汽车的速度是多大.

图6

解析：把超声波视为弹性波包，碰撞汽车后原速率反弹.可视为是波与汽车的相遇问题.以测速仪为参照，画出汽车和超声波的位移图线，如图6(c)所示.由图(c)可以看出，汽车在收到两个超声波的时间内产生的位移为

代入数据得

Δx=510 m

相应的时间间隔为

代入数据得

车速

v≈17.9 m/s

4 等效替换法

【例6】有两个质量相等的小球，在光滑的水平平直滑槽AB内运动，滑槽的两端有固定的壁.两球之间及球与壁之间的碰撞是完全弹性的，且碰撞时间忽略不计.开始时,两球分别位于将滑槽三等分的两个分点处，两球运动方向相同，速度不等.求：

(1)若两球之间的第二次碰撞是在滑槽中点迎面相碰，求两球的初速度之比.

(2)若两球之间的第6次碰撞是在滑槽中点迎面相碰，求两球初速度之比，满足要求的解有几种.

解析：两球等质量进行弹性碰撞，每次碰撞速度交换.故可等效为速度不等，在AB间来回运动互不干扰的隐形小球.画出两球来回运动的位移锯齿线图像，交点即为碰撞点，如图7所示.

图7

设A，B相距为3l，靠近A壁小球1速度为v1，靠近B壁小球2速度为v2.

(1)从位移图线可以看出，两个小球第二次在中点迎面相碰一定满足

v1t=2l+1.5l

v2t=l+3l+1.5l

所以，速度比

(2)两球最后一次在两壁中间相碰，位移须满足条件

v1t=2l+3nl+1.5l

v2t=l+3ml+1.5l

速度比

式中n,m分别为两小球在A,B壁间来回碰撞次数.

根据小球初速度分两种情况讨论：

1)若v2>v1，球2碰壁频率高，m>n.球2第一次碰壁反弹后才会与球1相遇，以后每从一壁到另一壁与球1碰撞一次，当第6次两球在中点迎面相碰时，对球2来说前面已碰撞了5次，故m=5.要迎面碰撞，位移图线斜率必须相反，也就n,m奇偶相异，故n只能取0,2,4.代入速度比公式得

2)若v1>v2，球1碰壁频率高，n>m.球1第一次碰壁前已经和球2发生过一次碰撞，第6次中点处迎面碰撞时，已在两壁间来回了4次，所以n=4.因为第6 次小球要迎面相碰，图线交点处斜率符号须相反，所以，m只能取奇数，取m=1或3.代入速度比公式得