四元数体上广义投射影矩阵和超广义投影矩阵*

曾月迪,潘素娟

(莆田学院 数学学院,福建 莆田 351100)

1997年Groβ和Trenkler在文献[1]中提出了复数域上广义投射影矩阵的概念，并刻画了广义投射影矩阵和超广义投射影矩阵的性质，矩阵的和、差、积的结果.2004年J K Baksalary等在文献[2]中进一步探讨了广义投射影矩阵和超广义投射影矩阵的性质.J K Baksalary等与武玲玲等分别在文献[3]和[4]中讨论了广义投影矩阵线性组合幂等的若干条件.本文考察四元数体上广义投射影矩阵和超广义投影矩阵的一些性质与应用.

Mn(H)表示四元数体上的n阶矩阵，C表示复数域，A*、trA、rankA、Rr(A)和Rl(A)分别表示A的共轭转置、迹、秩、右列空间和左列空间.

约定:酉矩阵记为H(n,U)={A∈Mn(H):AA*=A*A=In}

正规矩阵记为H(n,N)={A∈Mn(H):AA*=A*A}；

部分等距矩阵记为H(n,PL)={A∈Mn(H):AA*A=A}={A∈Mn(H):A+=A*};

EP矩阵记为H(n,EP)={A∈Mn}={A∈Mn(H):AA+=A+A};

四幂等矩阵记为H(n,QP)={A∈Mn(H):A4=A}.

定义1n阶矩阵A为广义投射影矩阵，若A2=A*，这里A*表示A的共轭转置.n阶矩阵A为超广义投射影矩阵，若A2=A+，这里A+表示的Moore-Penrose逆.我们约定H(n.GP)={A∈Mn(H):A2=A*},H(n,HGP)={A∈Mn(H):A2=A+}.

本文利用奇异值分解刻画了四元数体上超广义投影矩阵，从而讨论了广义投射影矩阵和超广义投影矩阵与几种重要的特殊矩阵之间的联系，并用不同的证明方法推广了文献[2]中的定理1和2，同时考察了他们在偏序中的若干应用.

1 广义投射影矩阵和超广义投影矩阵

引理1 设A∈Mn(H)，且A∈H(n,U)，那么

定理1 设A∈Mn(H)，且rankA=r,其奇异值分解为：

A=Udiag(D,0)V*,

①

其中D为r阶正对角阵，U，V∈H(n,U)，则

(1)A∈H(n,PL)当且仅当D=Ir；

(2)A∈H(n,HGP)当且仅当V*U=diag(U1,U2)，U1∈Mr(H)，且(U1,D)3=Ir.

证明 由①易见A的Moore-Penrose逆为A+=Vidag(D-1,0)U*.若A∈H(n,PL)，则Vdiag(D-1,0)U*=Vdiag(D,0)U*.因此D=D-1.又由于D为对角矩阵，则D=I.反之显然.

由定理1和奇异值的分解方法，我们可得到

定理2 设A∈Mn(H)，且rankA=r，则以下陈述等价：

(1)A∈H(n,GP)

(2)A∈H(n,QP)∩H(n,PL)∩H(n,N)

(3)A∈H(n,QP)∩H(n,N)

(4)A∈H(n,QP)∩H(n,PL)

证明 (1)⟹(2)由于A∈H(n,GP)，则A2=A*.由此可得

AA.*A=A4=(A*)=A,AA*=A3=A*A,A*AA*=A5=(A*)*A=A2=A*，

因此A∈H(n,GP)⊆H(n,QP)∩H(n,PL)∩H(n,N)

(2)⟹(3)、(4)显然.

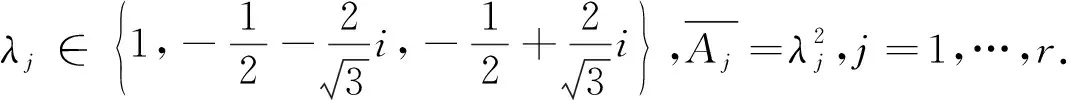
由U1U1*=PTT*P*，得trU1U1*=trTT*=r.注意到式子U1U1*+U2U2*=Ir，知U2=0.又由引理1知U3=0.由此经演算得A2=A*.

推论1 设A∈Mn(H)，且rankA=r，且其奇异值分解如①所示，则A∈H(n,GP)⟺V*U=diag(U1,U2),U1∈Mr(H),U13=Ir，且D=Ir.

证明 充分性显然.由定理1和2知D=Ir，又由定理2(4)⟹(1)可知必要性成立.

以下定理用不同的证明方法推广了[2]中的定理1和2.

定理3 设A∈Mn(H)，且rankA=r，那么

(1)A∈H(n,HGP)⟺A=Hdiag(T,0)H*,其中H∈H(n,U)，且T为上三角矩阵，对角元素

(2)A∈H(n,GP)⟺A=Hdiag(T,0)H*,其中H∈H(n,U)，且T=diag(λ1,λ2,…,λr),

注1 由上述定理易知广义投射影矩阵一定为超广义投射影矩阵.

2 偏序应用

自20世纪七八十以来，矩阵偏序的研究一直备受人们观注，在这一节，我们考察广义投射影矩阵和超广义投射影矩阵在减序、左星序、右星序、星序中的部分应用.

定义2[5]设A，B∈Mn(H)，

2)若A*A=A*B，且Rr(A)⊆Rr(B)，则记A*≤B.

3)若AA*=BA*，且Rl(A)⊆Rl(B)，则记A≤*B.

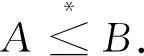
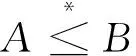
现证A*≤B⟹A≤*B.由[5]定理7.3.1存在U,V∈H(nU)，使得

推论2 设A，B∈Mb(H)，那么

2)若A*≤B，则Β≤H(n,PL)⟹A∈H(n,PL)；

3)若A≤*B，则B∈H(n,PL)⟹A∈H(n,PL).

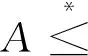
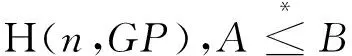
定理5 设A,B∈Mn(H)，那么

(2)若A*≤B,B∈H(n,HGP)，则A∈H(n,EP)⟺A∈H(n,HGP)；

(3)若A≤*B,B∈H(n,HGP)，则A∈H(n,EP)⟺A∈H(n,HGP).

证明 由EP矩阵与超广义投射影矩阵的定义，显然A∈H(n,HGP)⟹A∈H(n,EP).若A*≤B,B∈H(n,HGP)，A∈H(n,EP)，由[5]定理7.3.1知存在U,V∈H(n,U),使得

其中V*U=diag(U1,U2,U3),U1∈Mr(H)，U2∈Mt-r(H).由B∈H(n,HGP)得(U1Dr)3=Ir.由定理1可知A∈H(n,HGP).因此，(2)成立.类似可证(1)，(3)成立.

定理6 设A，B∈Mn(H)，那么

(2)若A*≤B,B∈H(n,GP)，则A∈H(n,EP)⟺A∈H(n,GP)；

(3)若A≤*B,B∈H(n,GP)，则A∈H(n,EP)⟺A∈H(n,GP).

证明 广义投射影矩阵一定为超广义投射影矩阵，由EP矩阵与超广义投射影矩阵的定义立得

A∈H(n,GP)⟹A∈H(n,EP).

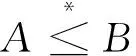
A=Udiag(Dr,0,0)V*,B=Udiag(Dr,D,0)V*

其中V*U=diag(U1,U2,U3),U1∈Mr(H)，U2∈Mt-r(H).由于B∈H(n,PL)，可得diag(Dr*,D*,0)diag((Dr)-1,D-1,0)，得Dr=I.又由B∈H(n,GP)，有下列等式diag(U1,U2,U3)diag(Ir,D,0)diag(U1,U2,U3)diag(Ir,D,0)diag(U1,U2,U3)=diag(Ir,D*,0).从而(U1)3=Ir.由推论1可知A∈H(n,GP).

影矩阵，A也未必为EP矩阵.因此上述两个定理中A∈H(n,EP)这个条件是不可缺的.例如

参考文献：

[1]Gro J,Trenkler G..Generalized and hypergeneralized projectors[J].Linear Algebra and its Applications,1997,264:463-474.

[2]Baksalary K,Baksalary O M,Liu J X.Further properties of generalized projectors[J].Linear Algebra and its Applications,2004,389:295-303.

[3]Baksalary K,Baksalary O M.On linear combinations of generalized projectors[J].Linear Algebra and its Applications,2004,388:17-24.

[4]武玲玲,刘晓冀.广义投影矩阵线性组合的研究[J].四川师范大学学报,2012,35(6).

[5]庄瓦金.体上矩阵理论导引[M].北京:科学出版社,2006.