单环环烷烃催化裂化动力学模型的建立——指前因子的计算
张 旭,郭锦标,周 祥,王鑫磊,于 博,葛彩霞
(中国石化 石油化工科学研究院,北京100083)
在流化催化裂化(FCC)工艺中,模型仿真正发挥着越来越重要的作用。模型仿真主要用来确定最佳工艺条件和评估潜在的原料。反应器的模型仿真主要包括反应器模型和动力学模型两方面[1-2]。
一维反应器数学模型通常是由一组常微分方程描述反应器内的组成、温度和压力变化与轴向位置的关系;对于反应器径向温度梯度显著的,就需要建立偏微分方程来描述反应器中不同位置的温度、压力等与组成的关系。
动力学模型描述的是反应器中化学计量的变化和化学反应速率的关系。烃类催化裂化过程遵循正碳离子机理[3]。基于正碳离子机理建立的动力学模型中包含反应物种和化学反应成百上千,使得建立分子层面的动力学模型变得十分困难[4-5]。早期建立的动力学模型,由于分析检测手段落后,用数量有限的虚拟分子来描述反应过程的化学计量学变化,即集总动力学模型。但是,随着分析表征技术的进步和环保要求不断提高,对各项指标的要求也越来越精细,集总模型已不能满足需求,需要建立预测能力更为精确的、适用范围更宽的分子水平动力学模型。
催化裂化分子水平动力学模型的研究始于20世纪80年代。单事件模型[6](Single-Event Kinetics)采取过渡态理论计算指前因子A,通过计算反应物和过渡态的单事件数比值获得反应熵变。这虽然在理论上可行,但是要计算整个复杂反应系统的反应物和过渡态分子构型十分繁琐,不具有现实的可行性。Willems等[7]系统地研究了热裂解过程中的指前因子的计算,应用过渡态理论和统计热力学相结合的方法,取得了较好的结果。但是对于催化裂化反应,还未见到有关方法的报道,主要是由于催化裂化反应过程涉及到十分复杂的反应物与催化剂之间的相互作用。
通过实验的方法回归出反应中的每一个化学反应指前因子,在实际操作上不具有现实可行性。为此,笔者结合过渡态理论和统计热力学的方法,建立了简单、快速获取甲基环己烷催化裂化主要反应的指前因子的方法,以期为单环环烷烃及多环环烷烃催化裂化动力学模型的建立提供数据支持。
1 建立单环环烷烃催化裂化动力学模型的理论基础和计算细节
通过过渡态理论结合统计热力学计算指前因子[8]。1935年,有研究者[8-9]在统计热力学和量子力学的基础上提出过渡态理论。他们认为,只要知道分子的振动频率、质量、核间距等基本物性,就能计算反应的速率常数,所以又称为绝对反应速率理论。笔者从过渡态理论出发,通过一定的假设和引进校正因子[10],用气相分子的平动熵近似代替难以获得的反应活化态的熵与反应物熵的差值[10-13],大大减少了工作量,简化了复杂程度,数据的准确度较高。
甲基环己烷(MCH)在分子筛上的催化裂化反应主要是由氢转移、异构化、质子化开环裂化、β-断裂、脱烷基和烷基转移6种主要反应类型所组成的复杂的串联、平行反应[14-15]。针对每一类反应,选取了几个典型反应作为代表,分别计算其指前因子,取平均值为每一类反应的指前因子值。
2 单环环烷烃催化裂化动力学模型
2.1 模型的建立
用经典的三配位正碳离子机理解释环烷烃的催化裂化,反应可以分为正碳离子的引发、转化和终止3个步骤。建立反应路径层面的动力学模型,可以采用实验中检测到的中间体和产物对其解释和完善。对于反应物、产物和中间体的计算机表达,反应规则的制定,相关参数的获取以及反应网络的建立,都是分子水平动力学模型中的重要组成部分。
建立动力学模型困难之一,是如何获取复杂反应体系中每一个反应的速率常数。要建立环烷烃催化裂化分子水平动力学模型,首先要解决的是反应活化能和指前因子。由于其反应的复杂性,不能够通过实验来获取所有的动力学参数,这在理论上和现实中都具有不可操作性。为此,需要建立一个相对简单、快捷的获取动力学参数的方法,这种方法应建立在准确的实验数据和相应的理论基础之上。
2.2 过渡态理论
Eyring[16-17]第1次定量描述过渡态理论。通过这一开创性的工作,后来的研究工作主要集中在理论研究,很少将理论成果运用于实际。Cohen[18]运用该理论获得了高温条件下的反应速率常数,Benson[19]将过渡态理论用于不同气相反应条件下的研究。
对于双分子裂化反应,根据过渡态理论可知,2个活化的原子或者分子需要经过碰撞,形成1个能量较高的活化络合物,反应物分子部分化学键断裂,形成新的化学键,最终形成产物。
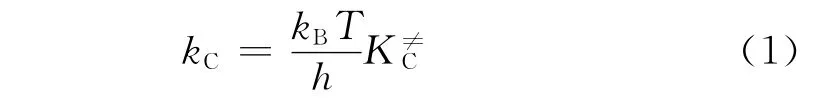
在推导式(1)过程中,每一个自由度的配分函数都分解出1个平衡常数。因此,K≠C也被称为修正平衡常数。为了方便使用,速率常数表达式可以用阿伦尼乌斯方程表达,由热力学关系式可以得到与过渡态理论相关的速率常数,如式(2)所示。将式(2)的前3项归为指前因子,如式(3)、(4)所示。
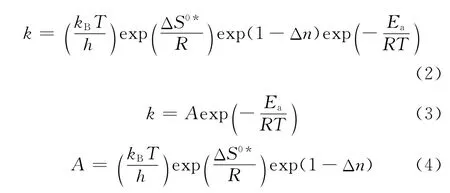
由式(4)可知,指前因子A被分作3部分,第1项表示的是过渡态的低频振动模式,第2项表示的是反应物和过渡态中间体之间的熵差,第3项是反应分子数的变化值。指前因子A与反应温度、反应分子数和活化熵差均有直接关系。反应温度、反应的分子数变化均可以直接获得,而唯一不能直接获得的是活化络合物与反应物之间的活化熵差。
在气相反应中,熵值大小主要与反应物和产物的结构有关。对于催化裂化反应这样复杂的反应系统而言,包含了反应物分子在催化剂上的吸附、扩散、化学反应和脱附过程,不仅实验中很难得到反应过程的活化络合物的熵,从理论上准确获取反应的活化熵也不现实。因此,根据文献调研和对实验数据的梳理,分析了不同类型的熵在整个反应中的变化,运用气相分子的平动熵与吸附态的熵差近似代替各种催化裂化反应整个吸附反应过程的熵变,而吸附态的平动熵为零。平动熵的表达式如式(5)所示:

根据阿伦尼乌斯公式,反应速率常数可以写为式(3)。提高反应速率可以通过提高反应温度,或者改变反应路径降低反应活化能来实现。另外,对于有催化剂参与的反应而言,通过改变催化剂制备的工艺条件,增加催化剂上的活性中心数,在一定程度上增加了活化分子的数量,换而言之,就是增大了指前因子A的数值。
2.3 指前因子的求取
表1为催化裂化反应中近似因子计算示例。由表1可知,计算结果与文献值吻合较好,也证明了前面的假设及引入校正因子的可行性。

表1 催化裂化反应中近似因子计算示例Table 1 Examples for the calculation of approximate factors for catalytic cracking reactions
催化裂化反应中参与反应的物种数和发生的化学反应数目成百上千。对反应过程分析和整理,发现甲基环己烷(MCH)在催化裂化催化剂上发生的主要反应有环烷环的开环反应、异构化、脱烷基、烷基转移、氢转移和β-断裂6大类反应类型,如图1所示。开环反应主要是以六元环的MCH及五元环的二甲基环戊烷为主。MCH异构为五元环分子是MCH转化的一个重要过程,同时开环裂化产生的链烷烃也可以发生异构化反应。MCH可以经过环烷烃和烯烃之间的氢转移反应形成苯、甲苯等芳烃分子和相应的烷烃。MCH经过2分子之间的烷基转移反应,生成C8和C6环烷烃,2分子甲苯会发生烷基转移反应,生成二甲苯和苯。在MCH催化裂化反应中可以检测到少量的甲烷和环己烯,甲烷的存在可以由脱烷基反应来解释。另外,MCH裂化生成的烯烃之间还会发生部分的叠合反应,芳烃的深度脱氢会生成焦炭。
表2为MCH催化裂化反应不同反应类别的指前因子数值。由表2可以看出,不同的反应类别指前因子数值相差很大。在计算过程中,采用了一些归并的措施,得到的指前因子数值与相关文献值[8,20]相吻合。
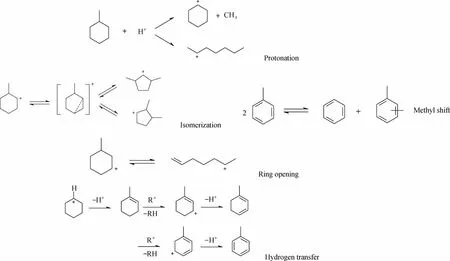
图1 MCH在催化裂化反应中的几种典型反应类型Fig.1 Typical reaction types in MCH catalytic cracking
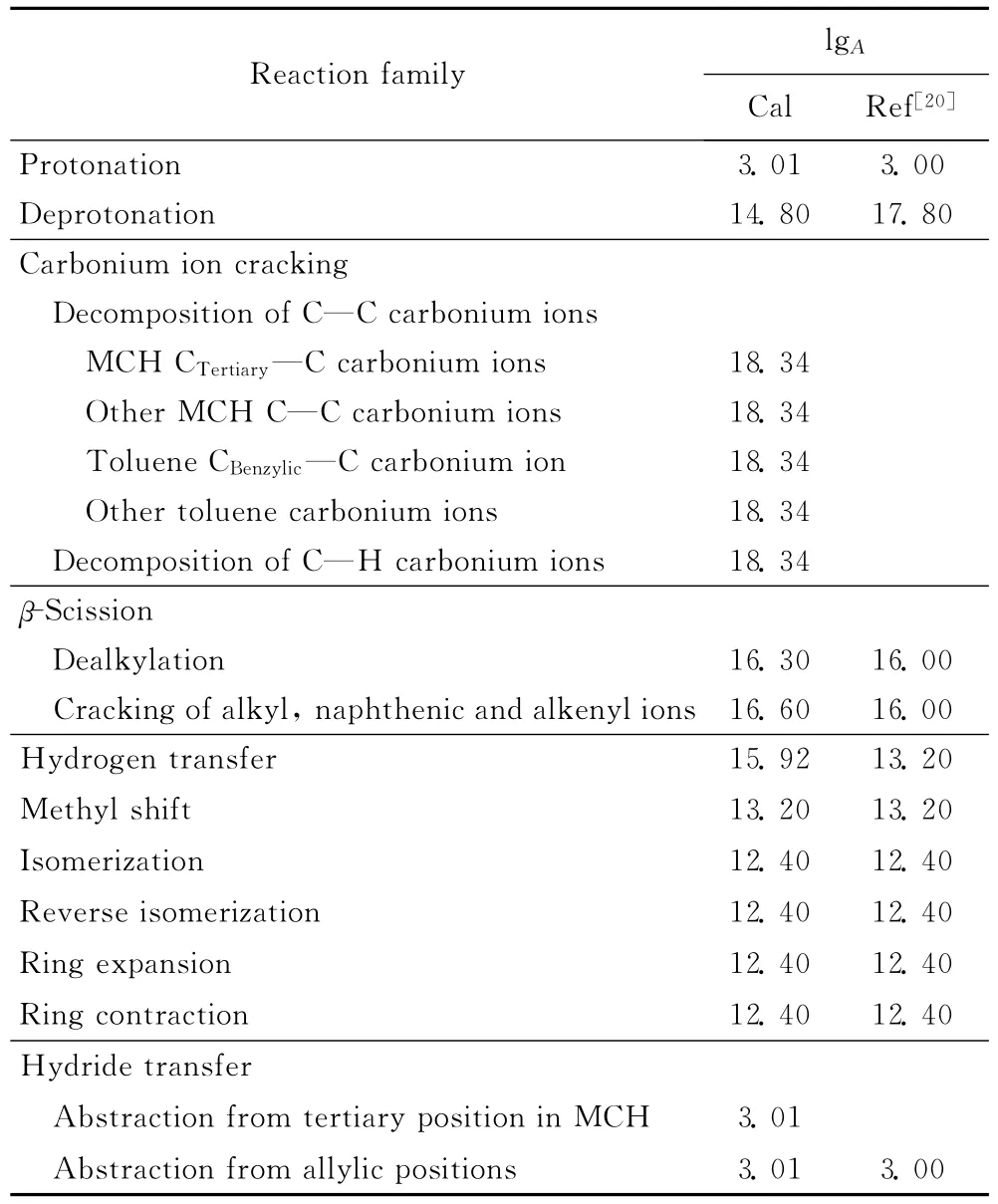
表2 甲基环己烷催化裂化反应中的指前因子Table 2 Arrhenius A factors for MCH cracking reaction families
对于催化裂化反应这样复杂的反应体系,不可能获得每一个基元反应的精确指前因子数值。对具有相似反应行为的化学反应,将其归为一个反应族(Reaction family),认为其指前因子数值是相同的,可以大大地减少所需的指前因子数目,然后通过实验结果对初始的指前因子数值进行进一步的优化。对同一类型的反应,采用反应族的方法是可行的,可以用来计算一类相似反应的指前因子[21]。在对复杂反应系统建模时,既要减少模型中参数数量,又要保证模型的准确性。对于某一特定反应,如果缺乏直接的动力学实验参数信息,在分子水平动力学模型建立的过程中,只要是可以归为同一反应族的反应,可以使用同一反应族的动力学参数值。
3 结 论
通过甲基环己烷催化裂化反应指前因子计算可以看出,过渡态理论和统计热力学可以成功地用于指前因子的求取。采取了气相分子平动熵变值近似代替反应过程中活化熵与反应物熵的差值,引入校正因子θ,简化了求解过程。分析了甲基环己烷催化裂化过程中发生的主要反应类型,计算了不同反应类型的指前因子数值,以其作为分子水平反应动力学模型中速率常数表达式中A的初始值,经过实验结果对模型参数的不断优化,最终得到准确度较好的指前因子A值。
符号说明:
A——指前因子;
Ea——反应活化能,J/mol;
h——Planck常数,6.62×10-34(J·s);
k——反应速率常数,速率系数的单位取决于反应的总级数;
kB——Boltzmann常数,1.38×10-23J/K;
kC——以浓度为标准的反应速率常数,速率系数的单位取决于反应的总级数;
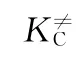
m——分子摩尔质量,g/mol;
M——处理后的分子摩尔质量,kg/mol;
NA——阿伏伽德罗常数,6.02×1023;
p——反应压力,kPa;
pCat——催化裂化反应熵差项近似值;
pCat,u——催化裂化单分子反应熵差项近似值;
pCat,b——催化裂化双分子反应熵差项近似值;
pCat,app——计算得到的催化裂化反应熵差项近似值;
pCat,ref——参考文献中催化裂化反应熵差项近似值;
R——摩尔气体常数,8.314J/(K·mol);
Sm,t——摩尔平动熵,J/(mol·K);
Str——平动熵,J/K;
T——反应温度,K;
V——体积,L;
Δn——过渡态与反应物之间的分子数变化,单分子反应其值为0,双分子反应为-1;
ΔS0*——气相活化熵差,J/(mol·K);
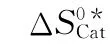
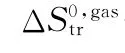
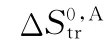
θ——校正因子,取值范围-1/2~1/2
[1]赵才先,于佐军,刘宝,等.流化催化裂化装置动态模型的建立及仿真软件的开发[J].石油学报(石油加工),2010,26(4):605-611.(ZHAO Caixian,YU Zuojun,LIU Bao,et al.Dynamic modeling and simulation software development for fluid catalytic cracking unit[J]. Acta Petrolei Sinica (Petroleum Processing Section),2010,26(4):605-611.)
[2]刘福安,侯栓弟,龙军,等.FCC汽油催化转化动力学模型[J].石油学报(石油加工),2005,21(6):32-39.(LIU Fuan,HOU Shuandi,LONG Jun,et al.Kinetic modeling of FCC gasoline catalytic reaction[J].Acta Petrolei Sinica (Petroleum Processing Section),2005,21(6):32-39.)
[3]许友好,龚剑洪,叶宗君,等.大庆蜡油在酸性催化剂上反应机理的研究[J].石油学报(石油加工),2006,22(2):34-38.(XU Youhao,GONG Jianhong, YE Zongjun,et al.Study on the reaction mechanism for Daqing VGO over acid catalyst[J].Acta Petrolei Sinica(Petroleum Processing Section),2006,22(2):34-38.)
[4]WEI W,BENNETT C A,TANAKA R,et al.Computer aided kinetic modeling with KMT and KME[J].Fuel Process Technol,2008,89:350-363.
[5]KUMAR H,FROMENT G F. Mechanistic kinetic modeling of the hydrocracking of complex feedstocks,such as vacuum gas oils[J].Ind Eng Chem Res,2007,46:5881-5897.
[6]FENG W,VYNCKIER E,FROMENT G F.Singleevent kinetics of catalytic cracking[J].Ind Eng Chem Res,1993,32:2997-3005.
[7]WILLEMS P A,FROMENT G F.Kinetic modeling of the thermal cracking of hydrocarbons 1Calculation of frequency factors[J].Ind Eng Chem Res,1988,27:1959-1966.
[8]杜梅西克,拉德,阿帕里西奥,等.多相催化微观动力学(沈俭一译)[M].北京:国防工业出版社,1998:25-40.
[9]王正烈,周亚平,李松林,等.物理化学(下册)[M].第四版.北京:高等教育出版社,2005:248-253.
[10]LEE J H,KANG S,KIM Y,et al.New approach for kinetic modeling of catalytic cracking of paraffinic naphtha[J].Ind Eng Chem Res,2011,50:4264-4279.
[11]LINDEMANN F A,ARRHENIUS S,LANGMUIR I,et al.Discussion on “the radiation theory of chemical action”[J].Trans Faraday Soc,1922,17:598-606.
[12]MARTENS G G,MARIN G B,MARTENS J A,et al.A fundamental kinetic model for hydrocracking of C8to C12alkanes on Pt/US-Y zeolites[J].J Catal,2000,195(2):253-267.
[13]QUINTANA-SOLóRZANO R.Single-event microkinetics for coking in catalytic cracking: Development and application[D].Gent:Universiteit Gent,2006.
[14]Al-SABAWI M,HUGO L.Kinetic modeling of catalytic conversion of methylcyclohexane over USY zeolites:Adsorption and reaction phenomena[J].AIChE J,2009,55(6):1538-1558.
[15]MATIAS P,LOPES J M,LAFORGE S,et al.Methylcyclohexane transformation over HMCM22 zeolite:Mechanism and location of the reactions[J].J Catal,2008,259(2):190-202.
[16]EYRING H. The activated complex in chemical reactions[J].J Chem Phys,1935,3:107-115.
[17]EYRING H.The activated complex and the absolute rate of chemical reactions[J].Chem Rev,1935,17(1):65-77.
[18]COHEN N.The use of transition state theory to extrapolate rate coefficients for reactions of OH with alkanes[J].Int J Chem Kinet,1982,14:1339-1362.
[19]BENSON S W.Thermochemical Kinetics[M].New York:Wiley,1976:79-90.
[20]WATSON B A,KLEIN M T,HARDING R H.Catalytic cracking of alkylcyclohexanes:Modeling the reaction pathways and mechanisms[J].Int J Chem Kinet,1997,29(7):545-560.
[21]WATSON B A,KLEIN M T,HARDING R H.Catalytic cracking of alkylbenzenes: Modeling the reaction pathways and mechanisms[J].Appl Catal A:Gen,1997,160:13-39.

