有限元计算网格划分对汽轮机转子应力计算结果的影响

邓志成，杨 宇，汪 勇，葛炼伟

（1．上海发电设备成套设计研究院，上海200240； 2．中核核电运行管理有限公司，嘉兴314300）

随着计算机技术的不断发展，有限元分析技术已经成为一种行之有效的工程分析手段，在汽轮机零部件的结构优化改进中得到了广泛的应用。有限元分析是将零部件的连续体离散化为有限个小单元，对每一单元假定一个合适的、较简单的近似解，然后分片逼近全求解域上的位置场函数。这些单元可以具有不同的形状，并以不同的连接方式进行组合，因此很容易分析几何形状复杂的汽轮机零部件的结构强度问题。

一般的汽轮机转子模型可以简化为二维轴对称结构，若有限元计算网格划分得当，可以通过有限元计算得到比较精确的应力场计算结果。而在汽轮机转子应力场的有限元计算过程中，同一个汽轮机转子模型，采用同一种边界条件，不同分析员的计算结果有时会有较大的差异，而出现这种情况的一个重要原因在于网格划分的差异。古松、宋少云、尹芳等作者已针对结构网格划分对有限元计算结果的影响进行过一些探讨［1－2］，但针对带有圆角的汽轮机转子的具体结构，研究网格划分对应力有限元计算结果影响的文章还比较少。开展本项研究工作，对于减少转子应力场计算过程中因网格原因引起的计算误差具有一定的指导意义。

1 计算模型

1．1 有限元计算模型

计算对象为某型号亚临界汽轮机高、中压转子，见图1。建立二维轴对称有限元模型，高、中压转子的热载荷为转子表面与蒸汽、空气和润滑油的对流传热系数［3］，先进行稳态额定负荷工况温度场计算，作为应力场计算的温度边界条件。高、中压转子各级叶轮所承受的叶片离心力和转子自身承受的离心力，作为高、中压转子等效应力场计算的应力边界条件。在计算中使用二维轴对称单元进行网格划分，并采用以下4种网格划分方案：

（1）方案1，采用三角形单元（ANSYS软件的PLANE183单元）进行智能划分网格，总单元数6 903。

（2）方案2，采用四面体单元（ANSYS软件的PLANE77单元）进行智能划分网格，总单元数3 010。

（3）方案3，采用四面体单元（ANSYS软件的PLANE77单元）设定单元边长为20mm进行网格划分，总单元数7 780。

（4）方案4，采用三角单元（ANSYS软件的PLANE183单元）进行智能划分网格后，将强度薄弱部位的网格局部加密一倍，总单元数7 228。

图1 高、中压转子有限元模型图

1．2 有限元网格细分的目标方案

在网格划分方面，经典的有限元理论认为，只要无限细分网格，就可以得到真实位移的下界［4］，也就是说当网格划分足够细的时候，有限元计算值将接近于真实值，即有限元的解出现收敛。为了确定该转子强度薄弱部位的应力，该高、中压转子采用四面体单元（ANSYS软件的PLANE77单元）进行不断细化，直到其应力集中部位的有限元计算解出现收敛，前后两次的等效应力计算结果的相对误差小于0．2%。此时，单元边长设定为5mm进行网格划分，并对强度薄弱部位的网格局部加密三倍，总单元数117 686，其应力场计算结果作为其他方案的比较值，其网格划分作为有限元网格细分的目标方案。有限元网格模型见图2。

图2 高、中压转子目标方案有限元网格模型

1．3 强度薄弱部位

根据稳态温度场和应力场的有限元数值计算，此高、中压转子的强度薄弱部位为高压第1级静叶前弹性槽底（部位A，圆角半径19mm）、调节级叶轮进汽侧根部圆角（部位B，圆角半径25mm）、调节级叶轮出汽侧根部圆角（部位C，圆角半径50mm）和调节级叶轮进汽侧圆角（部位D，圆角半径3mm），见图3。目标方案的强度薄弱部位有限元网格模型见图4，按照4种方案，进行等效应力的有限元计算，得出部位A、部位B、部位C和部位D的等效应力，并对计算结果进行分析。

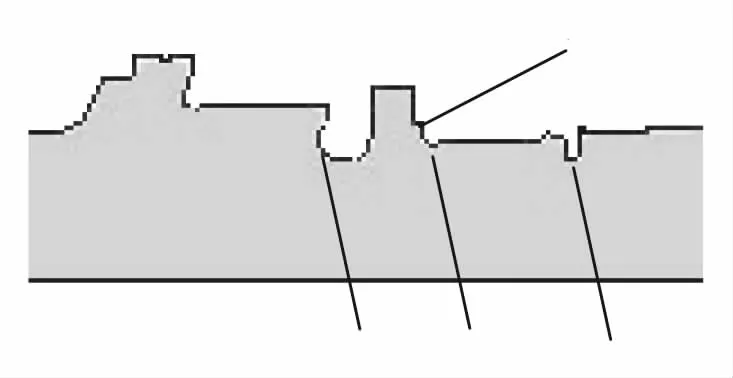
图3 高、中压转子强度薄弱部位

图4 高、中压转子目标方案的强度薄弱部位限元网格模型

2 结果与分析

2．1 等效应力计算结果

不同网格划分方案中汽轮机高、中压转子强度薄弱部位等效应力计算结果与目标方案等效应力计算结果的比较见表1。从表1中可知：在所有方案中，部位D的等效应力最大，部位A的等效应力最小。

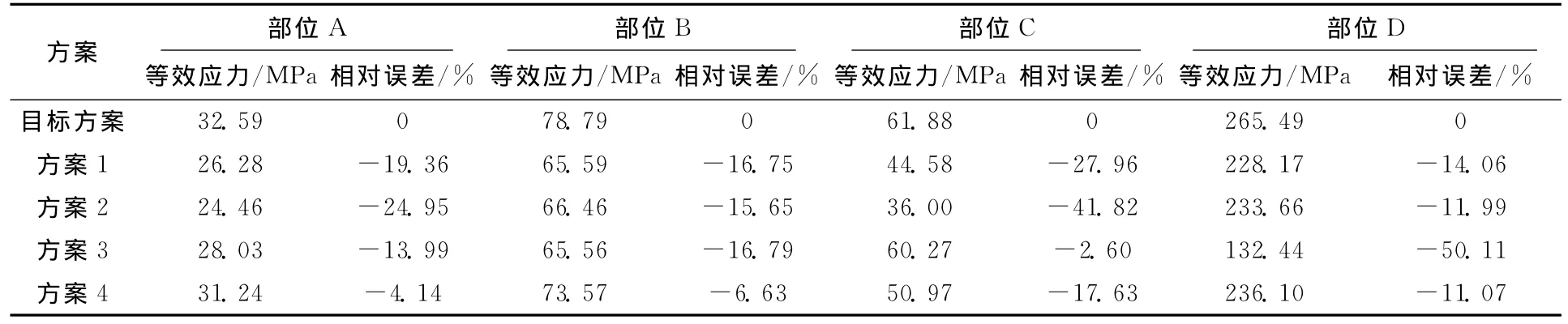
表1 高、中压转子不同方案应力场计算结果

2．2 分析与讨论

由表1给出的汽轮机高、中压转子等效应力的计算结果，绘制出不同方案计算结果与目标值的相对误差绝对值的柱形图，见图5；方案1与方案4计算结果与目标值的相对误差绝对值的柱形图，见图6。由表1和图5、图6可以看出：

（1）各个方案等效应力的计算结果与目标方案大多有较大的差距，最大相对误差达到了50%，原因在于网格划分较粗，单元数较少。

（2）方案1和方案2等效应力的计算结果比较接近，这两种方案采用网格智能划分。

（3）相比于目标方案等效应力的计算结果，方案3的D部位等效应力的结果差异比较大，原因在于方案3没有采用智能划分网格。

（4）对于有大圆角或者小圆角部位，一般需要进行局部网格加密才能得到比较准确的计算结果。

（5）与方案1相比较，采用局部加密网格的方案4，等效应力计算结果的误差明显下降，但仍与目标方案等效应力的计算结果有一定差距。

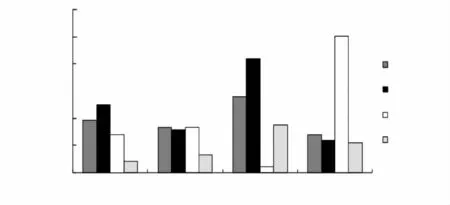
图5 不同方案计算结果与目标值的相对误差值的对比

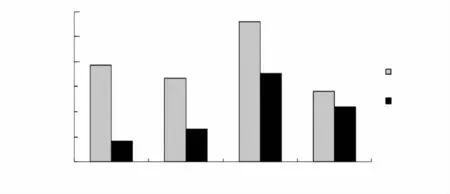
图6 方案1与方案4计算结果与目标值的相对误差值的对比

3 结语

通过对汽轮机高、中压转子强度薄弱部位等效应力的有限元计算分析得出：

（1）对于汽轮机转子二维轴对称有限元模型，若采用三角形单元或者采用四边形单元智能划分网格的方法，对计算结果的影响不大，但由于采用四边形单元进行网格划分，单元总数要远小于采用三角形单元，而单元数量的减少意味着计算速度的提高。对于汽轮机转子的二维轴对称模型，若模型结构比较复杂，无法使用四边形单元的情况下，可以采用三角形单元，并不影响等效应力计算结果的准确性，但需要较长的运算时间。

（2）对于汽轮机转子圆角部位，采用智能划分若不对其进行局部细化，计算结果有较大的误差，无法反映圆角部位真实的应力状况，尤其对于圆角半径很大或很小的部位，局部细化一倍也不一定到达预期效果，必须经过反复试验，多次局部细化。

（3）网格细分直到前后两次等效应力的计算结果的相对误差小于0．2%为止。这样即使由不同人员划分网格，也能得到相近的有限元计算结果。

［1］古松．网格划分方式及密度对有限元模型计算结果的影响［J］．中国水运，2006，6（10）：122－123．

［2］宋少云，尹芳．有限元网格划分中的圣维南原理及其应用［J］．机械设计与制造，2012，33（8）：63－65．

［3］史进渊，杨宇，邓志成，等．大功率电站汽轮机寿命预测与可靠性设计［M］．北京：中国电力出版社，2011．

［4］Logan D L．有限元方法基础教程［M］．伍义生，吴永礼，译．3版．北京：电子工业出版社，2010．