预应力墩基础的抗倾覆承载力研究

郭敏，申超

（1. 中国船舶重工集团有限公司第七一三研究所，郑州 450015；2. 北京中水恒信环境科技发展有限公司，北京 100107）

预应力墩基础的抗倾覆承载力研究

郭敏1,2，申超1

（1. 中国船舶重工集团有限公司第七一三研究所，郑州 450015；2. 北京中水恒信环境科技发展有限公司，北京 100107）

随着风电机组容量的逐渐增大，传统风电机组基础形式已经不能满足使用要求，必须要在传统基础上进行创新。预应力墩基础预应力墩基础作为一种新型基础，在适用范围、安全性能以及建造成本上具有一定优势。该文通过研究预应力墩基础的抗倾覆验算方法，为计算这种新型基础的抗倾覆承载力探索一种快速、合理的方法。

风电机组；预应力墩基础；抗倾覆承载力；地基反力系数法；极限平衡法；有限元法

0 引言

在文献[1]中明确提出，当桩基础桩长小于6m或桩长虽大于6m但基础长度与直径之比小于3时，即为墩基础。墩基础用作风电机组基础，主要承受水平力和力矩，因此其抗倾覆承载力成为设计的控制因素。

1 墩基础抗倾覆计算研究现状

研究人员在基础水平承载力分析中已经得出许多可行的计算方法。关于墩基础抗倾覆计算理论，目前主要借鉴刚性短桩以及大圆筒结构的分析方法：地基反力系数法、极限平衡法和有限元数值模拟。

1.1 地基反力系数法

地基反力系数指的是土压力同其相应的位移的比值，该值随许多相关因素变动。这一方法不考虑基础同土之间的摩擦阻力和粘结力。在水平荷载或偏心竖向荷载或两者共同作用下，基础发生刚体转动，转角为w，转动中心在地面下深度为Z0。基础转动时施加于土的水平压力由地基反力系数同位移的乘积来表达。基础底面的竖向力同样由地基反力系数同地基土的压缩量乘积来算得。然后建立水平向力和对某点力矩的平衡方程，便可以得出基础的旋转角和转动中心。这种方法只能得出在已知外力条件下基础的旋转角度和中心，根据文献[2]提出的转角控制值，可以求解出基础在极限转角下的抗弯承载力。

1.2 极限平衡法

极限平衡法首先假定极限状态的地基土反力分布形式，再按照土的极限静力平衡来求解基础的抗倾覆承载力。作用于基础的极限状态的地基土反力有多种分布形式，如抛物线、三角形、矩形等[3]，如图1所示。目前比较常见的有从弹性半空间应力状态出发推导而得的朗肯土压力理论、适用于软黏土的Murff－Hamilton理论以及Borm提出的反力分布形式等。

1.3 有限元数值模拟

有限元数值模拟作为最普遍的数值分析方法，不仅考虑了极限平衡分析中的平衡条件和破坏条件，同时还满足变形协调条件，考虑土体的应力应变特性、土体和基础的相互作用。但是由于墩基础体型庞大，若用有限元分析，需要划分较多的单元才能反应实际情况，因此需要较高的硬件配置和一定的计算时间。

2 极限平衡理论

2.1 侧向土压力

极限平衡法首先要假定极限状态的地基土反力分布形式。本文根据需要，并未直接采用1.2节所述的任何一种方法，而是采用文献[4]中的取值方法。侧向土压力由两部分组成：正面土体抗力Q和侧面土体抗力F，如图2所示。

因此，极限侧向土压力pu可用下式表示：

建设综合立体交通走廊，把云南建成长江上游地区重要的交通枢纽。习近平总书记视察云南时明确要求，云南要加快建成面向南亚东南亚的辐射中心。紧扣这一目标要求，云南要着力推进长江上游干线和骨架支流航道治理，加快长江上游航运中心建设步伐。统筹推进铁路、公路、航空交通运输发展，大力发展铁水联运、江海联运、铁空联运等多式联运，构建起多种运输方式优化布局、相互衔接的交通网络体系。

式中：B——基础直径或宽度；

η，ξ——分别为正面和侧面土压力不均匀分布系数：

对于圆形基础：η=0.8，ξ=1；

对于方形基础：η=1.0，ξ=2.0；

pmax——正面土压力；

τmax——侧面土压力。

研究人员在正面土压力pmax的求解上做了比较全面和完善的理论和试验研究，如朗肯土压力理论、Borm提出的土压力理论或者Muff-Hamilton理论，实际应用时结合工程实际进行取值。侧面土压力τmax目前没有在文献中找到确切的取值方法，不过可以近似采用桩基础侧摩阻力的取值方法[4]，至于桩基础侧摩阻力的取值方法在API规范[5]中有明确的规定。

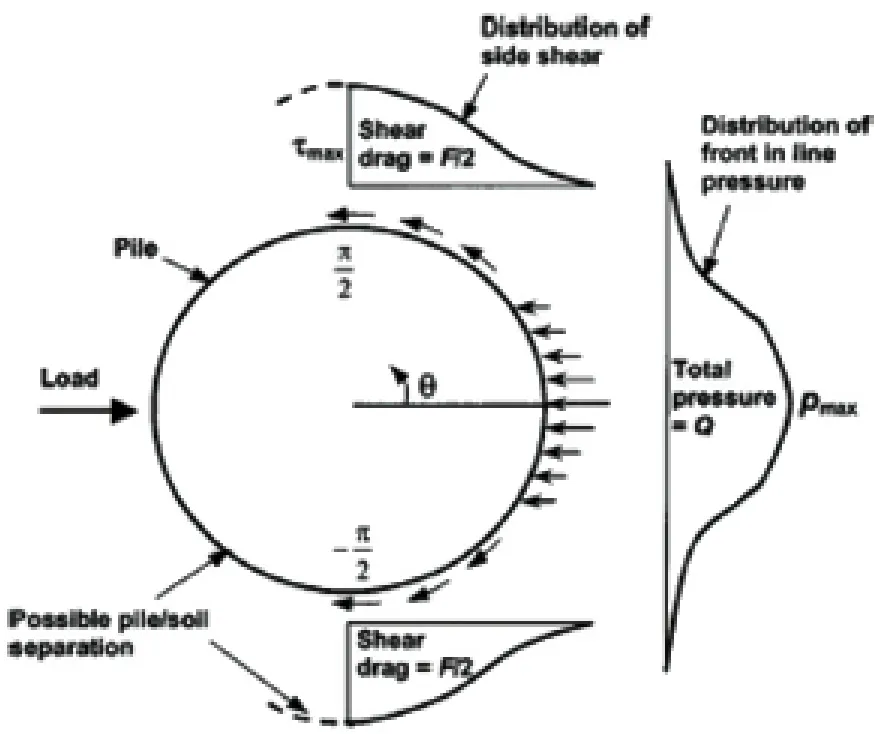
图2 侧向土压力示意图[4]

表1 某风电场地质条件

2.2 计算思路

极限平衡法的分析思路为建立受力模式和各种假设－得出平衡方程－得出旋转中心－得出极限承载力。方法的流程为根据平衡方程得出旋转中心，然后考虑对抗倾覆贡献的几项因素，最后汇总为极限抗倾覆能力。其中对抗倾覆贡献的几项因素包括：侧向土压力贡献部分，基底切向力贡献部分，基底竖向力贡献部分以及侧摩阻力贡献部分，可以根据实际需要考虑其中几项或者全部对基础抗倾覆承载力的贡献。

3 工程实例

3.1 地质条件

本文以某风电场2.5MW风电机组为例，进行预应力墩基础抗倾覆验算。该风电场地质条件如表1所示。

本风电场场址区存在季节性冻土，其标准冻深线深度为地面以下1.2m左右，因此底面向下0－1.2m只考虑重力荷载，不作为持力层。

3.2 基础尺寸和设计荷载

基础示意图如图3所示，基础相关尺寸如下：

基础埋深：9500mm；

基础开挖直径：顶部8500mm，底部7000mm。

荷载坐标系如图4所示，荷载采用极限荷载修正标准值，如下：

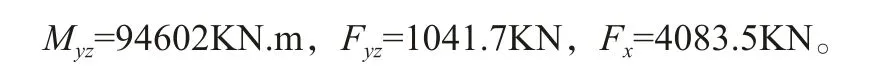
3.3 计算结果分析

根据2.1和2.2节，采用极限平衡法计算出来的结果如表2所示。

为进行对比，同时采用有限元数值模拟进行对比分析。计算模型如图5所示。

基础稳定性计算参照文献[2]中8.5“稳定性计算”规定。

预应力墩基础的受力特性是主要由基坑侧壁为主提供抵抗力，因此抗倾覆力矩为基坑土的抵抗力矩与基础重力力矩之和，而基坑土的抵抗力矩与基坑土受压情况有关，即基础受外力越大，倾斜度越大，基坑土提供的抵抗力矩越大。所以，抗倾覆力矩与基础倾斜度正相关。对于不同的控制倾斜率，将具有不同的抗倾覆系数。

表2 极限平衡法计算结果

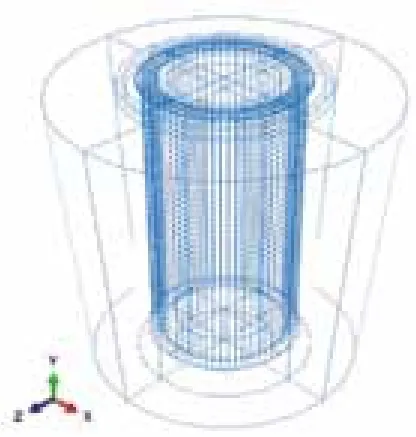
图3 基础结构示意图

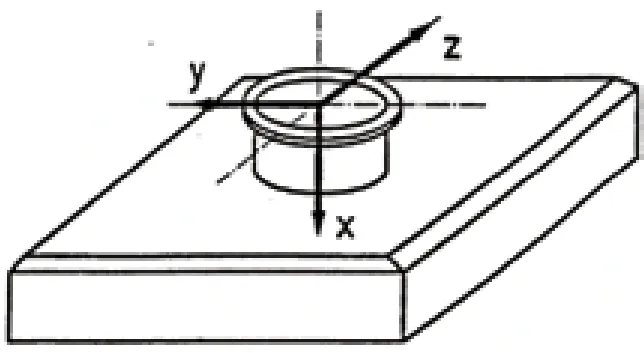
图4 荷载坐标系

图5 有限元计算模型

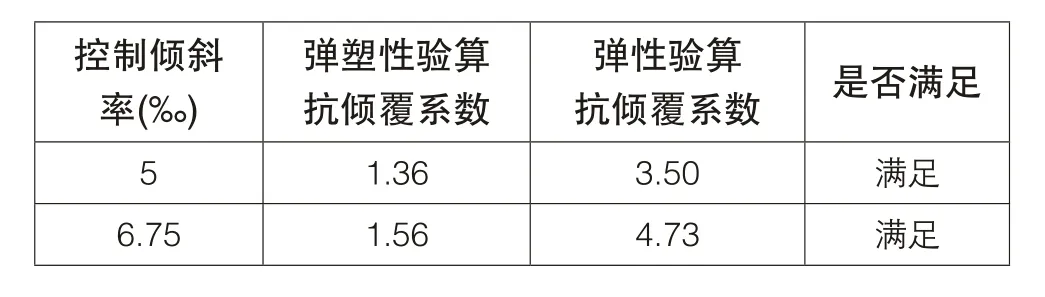
表3 有限元数值模拟结果

在本次计算中，采用弹塑性和弹性2种计算方法进行验算，计算结果如表3所示。

上述抗倾覆系数均对应于控制荷载工况的荷载修正标准值。

在极限荷载(荷载修正标准值)的作用下，基础的倾斜率是2.82‰。

4 结论

由于水平荷载和力矩作用下基础与土的作用机理比较复杂，虽然研究人员已经提出不少相关理论和计算方法，但是都各有不足以及优点。本文通过比较有限元数值模拟结果和极限平衡法计算结果，极限平衡法计算结果偏保守，可以作为有限元分析的一种补充算法。

[1] 结构/建设部工程质量安全监督与行业发展司, 中国建筑标准设计研究所. 全国民用建筑工程设计技术措施-结构[M]. 北京: 中国计划出版社, 2003.

[2] FD003-2007, 风电机组地基基础设计规定 [S]. 北京 : 中国水利水电出版社 , 2008.

[3]张雁 , 刘金波 . 桩基手册 [M]. 北京 : 中国建筑工业出版社 , 2009.

[4]Zhang, L.Y., Silva, F., Grismala, R. Ultimate lateral resistance to piles in cohesionless soils [J]. Journal of geotechnical and geoenvironmental engineering, 2005, 78-83.

[5] American Petroleum Institute. Recommended practice for planning, designing and constructing fixed offshore platforms-working stress design: API recommended practice 2A-WSD (RP 2A-WSD) [M]. American Petroleum Institute, 1993.

Research on the Anti-overturning Bearing Capacity of Wind Turbine Prestressed Pier Foundation

Guo Min1,2, Shen Chao1
(1. 713thResearch Institute of China Shipbuilding Industry Corporation, Zhengzhou 450015, China;2. ZSHX Environ-tech Co., Ltd., Beijing 100107, China)

As the gradually increasing of wind turbine capacity, traditional wind turbine foundation type can no longer meet the operating requirements. It is necessary to make innovation based on the traditional foundations. As a new type of wind turbine foundation,the prestressed pier foundation has advantages on the application range, safety performance and construction costs. This paper researched and explored a fast and reasonable method for computing the anti-overturning bearing capacity of wind turbine prestressed pier foundation through studying several calculation methods.

wind turbine; prestressed pier foundation; anti-overturning bearing capacity; modulus of subgrade reaction method; limit equilibrium method; fi nite element method

TU470+.3

A

1674-9219(2013)11-0114-04

2013-10-11。

郭敏（1987-），女，硕士，助理工程师，主要从事风电机组基础设计工作。