盾构隧道地震响应分析方法及工程应用

赵武胜，何先志，陈卫忠，杨建平，王 辉，袁敬强

（1. 中国科学院武汉岩土力学研究所 岩石力学与工程国家重点实验室，武汉 430071；2. 中交第二公路勘察设计研究院有限公司，武汉 430056）

1 引 言

由于盾构法隧道具有目标工期及工程造价可控性好、风险相对较小等优点，在国内外隧道工程中被广为采用。但盾构隧道存在大量连接缝，整体性差，抗震性能低于一般隧道。1985 年墨西哥M8.1级地震中，地下输水盾构隧道发生管环相对错位连接螺栓被剪断、管片端部混凝土脱落等震害；1995年日本兵库县南部M7.2 级地震中，部分盾构隧道管片接头破坏，接头附近混凝土破损出现裂缝发生漏水[1]。尤其对越江盾构隧道，其一般处于地下水位以下，防水要求很高，一旦经历地震作用发生类似震害，将会严重影响隧道的安全。因此，开展盾构隧道地震响应研究意义重大。

目前地下结构抗震分析手段主要有原位观测、模型试验及理论分析。由于地震的偶然性导致原位观测资料较少，而模型试验受到尺寸和相似比的限制又难以真实反映隧道地震响应。因此建立合理的理论分析模型及高效的计算方法成为地下结构抗震分析的重要内容。

对盾构隧道管片及接头的地震响应研究，目前多采用自由圆环模型、多铰圆环模型、梁-弹簧模 型[2－3]、薄壳-弹簧模型[4－5]等。而这些模型大都将接头模拟成弹簧单元，难以模拟接头与管片的相互作用；将管片模拟成梁或薄壳单元，难以模拟管片之间及管片与围岩土体间真实的相互作用；目前考虑隧道管片与围岩之间相互作用时，一般不考虑管片与围岩之间及管片之间的相对滑移与分离。而实际震害表明，在地震荷载作用下，尤其当管片与围岩力学性质差别较大时，可能出现接触非线性[6]。

本文采用梁单元模拟接头单元，并将梁单元嵌入实体厚壳中，反映了接头与管片间的相互作用；采用厚壳单元模拟管片，考虑管片间及管片与土体间的挤压与摩擦作用，分析了接触非线性对管片接头动力响应的影响；近似考虑了封顶块的楔形角度及错缝连接，采用无限元动力人工边界，建立了厚壳-接触-无限元盾构隧道动力分析模型。

2 计算模型

2.1 接头

管片连接螺栓为盾构隧道最易发生破坏的部位，接头在实际的受力过程中主要受拉与抗剪，抗弯与抗压性能则主要由管片间的相互挤压与摩擦来承担，且连接螺栓与管片可发生相互作用。均质圆环模型未考虑接头单元，梁-弹簧模型及薄壳-弹簧模型又将抗弯、抗剪性能集中在接头上，与实际管片接头受力有较大差异[7]。采用梁单元模拟接头，并将梁单元嵌入到管片单元中，既可模拟接头的抗拉、压、剪力学性质，也可模拟接头与管片之间的相互作用。

2.2 管片

通常采用梁或薄壳单元模拟管片，但梁单元及薄壳单元不能很好地模拟管片之间相互作用。薄壳理论是建立在基尔霍夫－乐甫假设（当结构厚度方向的尺寸远小于其他方向，并忽略厚度方向的应力）的基础之上的，而盾构隧道管片的厚度与幅宽之比一般稍大于1/5，不能满足上述假设，同时管片厚度方向的应力也不宜忽略，因此，管片宜使用厚壳单元进行模拟（见图1）。采用厚壳单元具有以下优点：

（1）采用厚壳单元可以考虑管片厚度及横向剪切应力及剪切应变。

（2）厚壳单元未引入常规壳单元中的转动自由度，因此，可方便地与实体单元连接，更好模拟管片与围岩之间的相互作用。同时对于描述动力作用下包括大转动在内的大位移问题较薄壳单元更适合。

（3）由于以上两点，在模拟管片之间接触关系时，厚壳单元考虑了双面接触中厚度的变化，厚壳单元比薄壳单元更精确。

（4）与采用实体单元相比，采用厚壳单元可以通过节点局部坐标系确定厚壳单元的厚度方向、环向、轴向，能很方便地分析管片轴向、径向、环向轴力及弯矩。厚壳单元相应的单元的轴力及弯距定义为

式中： SF 1、 SF 2、 SF 6为厚壳单元局部坐标系中3 个主方向的轴力； SF 3、 SF 4、 SF 5为厚壳单元局部坐标系中3 个主方向的剪力；h 为单元厚度；σ11、σ22、σ12、σ13、σ23、σ33为单元的应力；z为单元厚度方向坐标。

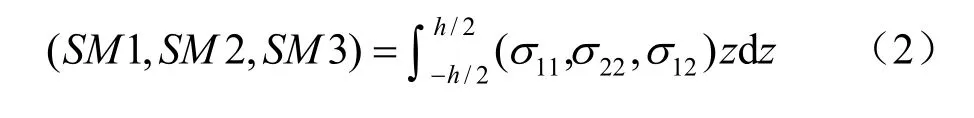
式中： 1SM 、 2SM 、 3SM 为单元关于局部坐标系3 个主方向的弯矩。

图1 盾构隧道管片有限元模型 Fig.1 Finite element model of segments of shield tunnel

2.3 人工边界

地震波传播至地下结构及介质发生变化处均会发生散射，当传播至地表面处又会发生反射。如在模型侧边及底边采用简单固定边界，地震波的散射波及反射波传播至人为划割的边界时会发生反射，这与实际地震波的传播过程不符，为了消除这种非真实反射波，需引入人工吸收边界，本文采用无限元动力人工边界。

（1）无限元作为一种常用的人工边界，它可模拟远场对地震波的吸收。

在边界地基为弹性及地震波为平面波的假定下，由虎克定律[8]可得

式中：σ 为地震波在无限弹性介质中产生的应力；ρ 为介质密度；c 为地震波速，压缩波对应pc ，剪切波对应sc ；ν 为地震波引起质点的振动速度，压缩波对应pν ，剪切波对应sν 。

无限元阻尼力定义为

式中：dampσ 为无限元阻尼力；d 为无限元阻尼常数，压缩波对应pd ，剪切波对应sd 。

对压缩波、剪切波引入无限元阻尼常数：

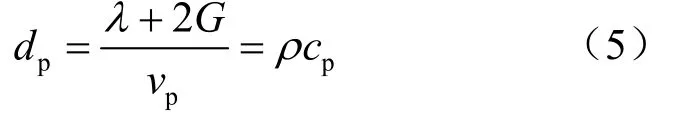
式中：λ，G 为弹性常数。

由式（4）～（6）代入式（3）可得

因此，引入以上无限元阻尼常数，无限元就可以充当吸收边界，吸收传向远场的地震波。

（2）无限元远端节点处位移默认为0，从而可模拟远场地基初始地应力及无穷远处位移为0 的边界条件。有限元-无限元耦合计算模型如图2 所示。

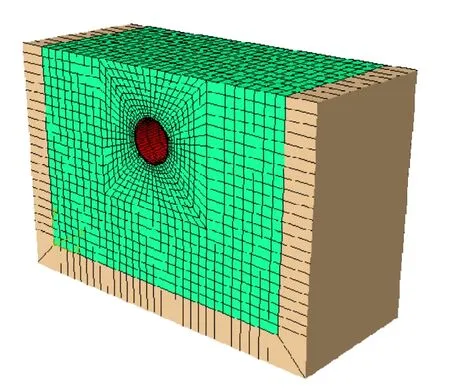
图2 有限元计算模型 Fig.2 Computational model of shield tunnel

3 管片与土体及管片间的相互作用

实际观测资料表明，在地震荷载作用下，特别是在围岩与管片力学性质差别较大时，会出现相对滑移和分离，即接触的非线性。同时，小泉[1]通过隧道横向反应的振动试验得出，由于地基位移和环向剪切力产生的断面内力，比率约为1：1，因此，进行盾构隧道横断面的抗震研究时，环向剪切力不可忽略。而能同时考虑管片围岩的接触非线性及环向剪切应力最有效的方式是建立起管片-管片、管片-土体间的接触非连续模型。

3.1 接触面法向力与位移关系

接触面法向力与位移关系采用惩罚刚度模型：

式中：P 为接触法向力；h 为嵌入量；ink 为接触面嵌入惩罚刚度； f 为惩罚函数。

事实上，管片之间及管片与土体之间相互接触过程中不存在相互穿透的情况，但数值计算中不可避免会出现接触面之间的穿透，如图3 所示，考虑法向接触力与接触面穿透量之间采用指数形式的惩罚函数关系。接触面穿透量可通过接触法向刚度及最大允许过盈量来控制。

图3 接触面法向力-位移关系 Fig.3 Relationship between force and displacement on contact surface

3.2 接触面切向力与位移关系

接触面切向力与位移关系采用Coulomb摩擦模型，接触面等效摩擦应力为

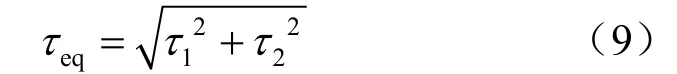
式中：1τ 、2τ 为摩擦面内两垂直方向剪切应力。

临界剪切应力为

式中：μ 为摩擦系数。

对于摩擦系数μ，经验数据表明，静摩擦系数与动摩擦系数不同，两者近似满足以下指数关系：

式中：kμ 为动摩擦系数；sμ 为静摩擦系数；cd 为折减系数；eqγ˙ 滑动应变率。

相对滑移发生条件：

当τeq≥τcrit时则发生相对滑移；

当τeq＜ τcrit时则不发生相对滑移。

各方向的滑移速度由下式确定：

式中：iτ 为i 方向的剪切应力；iγ 为i 方向剪切滑移速度；eqγ 为总的剪切滑移速度。

3.3 计算方法

有限元软件ABAQUS 中的显示动力分析方 法[9]对爆炸、冲击、高速动力等非线性问题十分有效且具有强健的接触功能甚至能够解决最复杂的接触模拟。采用该分析方法可以迅速建立起复杂的接触关系且可解决其他计算方法耗时过长等问题，从而使该模型进行动力分析简单且实用。

4 工程应用

4.1 场地基本资料

某越江隧道为双线双层八车道，工程场地存在6 条大的破碎带及4 条小型破碎带，近场区遭遇6.0级以上地震3 次。地震基本烈度为Ⅶ度，暂按Ⅷ度设防。根据地基土波速试验，场地20m 为浅平均剪切波速约为120 m/s，根据规范[10]，判定场地土类型为软弱土，建筑场地为Ⅲ类，场地特征周期为0.45 s，场地所处的抗震地段为不利地段，地层计算参数见表1。隧道最大设计水深约为62 m，最小埋深约为20 m。管片外径为14.5 m。属于大直径、高水压穿越液化地层和破碎带的盾构隧道，进行抗震研究是必要的。

表1 隧道穿越地层计算参数 Table 1 Computational parameters of soils of tunnel passing though

4.2 管片基本参数

普通衬砌环由钢筋混凝土构成，混凝土强度等级为C60。衬砌环分10 块，具体分为7 块标准块、2 块邻接块和1 块封顶块。管片采用错缝连接，内径为13.3 m，幅宽为2 m，厚度为60 cm。每个纵缝采用3 根M36 螺栓，环缝采用42 根M30 螺栓连接。

4.3 地震动输入

参照地震安评报告，场地设计地震动加速度按100 a 基准期超越概率2%的地震加速度取值，峰值加速度为0.2 g，波形采用1940 年美国帝国谷EI-CENTRO 地震（南北向，震级为M6.7，震中距为9.3 km，最大加速度为2.49 m/s2，持续时间为 25 s）中的加速度时程作为输入地震动。并将EI-CENTRO 波峰值等比例放大，从而得到100 a 2%场地基岩设计加速度时程曲线（见图4）。地震动输入分横向和竖向2 个方向进行，竖向设计地震动峰值加速度取水平向的2/3，采用底部输入方式。

图4 EI-CENTRO 地震加速度-时程曲线 Fig.4 EI-Centro earthquake acceleration history curve

4.4 计算结果

管片轴力、弯矩：地震荷载作用下，由于管片直径较大，埋深较浅，管片顶部与底部竖向压力差较大。环向轴力（见图5）与弯矩（见图6）沿厚度方向变化明显，环向拉伸轴力主要分布在拱顶和拱底的内侧及两侧拱腰的外侧。管片厚度方向轴力（图见7）在管片连接缝处出现非连续性，且在管片接头处出现明显的应力集中现象。

管片变形：从放大20 倍的变形图（见图8）可以看出，在管片连接处，刚度发生突变，在地震荷载作用下导致环内接头两侧管片及环与环之间发生了相对滑移与分离现象。

接头轴力、剪力及弯矩：从图9、10 可以看出，在管片连接处，接头轴力、剪力及弯矩较其他位置明显偏大。这是由于在管片接触处，管片刚度降低，在动力作用下连接缝两侧管片有相对错动的趋势，接头在此处受力较大，易发生剪断破坏。

图5 管片环向轴力（单位：N） Fig.5 Axial force in circumferential direction (units: N)

+5.617×105-2.431×104-6.103×105-1.196×106-1.782×106-2.368×106-2.964×106

图6 管片环向弯矩（单位：N·m） Fig.6 Moment in thickness direction (units: N·m)

图8 放大20 倍管片变形 Fig.8 Segment deformation after 20 times magnification

图9 管片接头轴力与剪力（单位：N） Fig.9 Axial force and shear force of connectors (units: N)

图10 管片接头弯矩（单位：N·m） Fig.10 Moment of segment connectors (units: N·m)

从轴力分析结果可以看出，管片在环内及环间接头处刚度发生突变，在地震荷载作用下发生应力集中现象，当应力达到一定值会发生管片剥皮破坏；同时从管片变形图可以看出，应力集中区刚度较小，地震荷载作用下连接缝两侧管片发生相对位移，如变形过大将引起管片漏水；正是由于管片的相对滑移，导致接头在管片连接缝处受力较大，管片的错动将会引起接头螺栓被剪断、接头处管片开裂等震害。上述计算结果与前言部分所述震害资料[1]相符，表明本文提出的模型能较好地模拟盾构隧道在地震作用下的受力破坏。

5 注浆层对管片动力响应影响

5.1 计算工况

盾构隧道壁后注浆层可尽早填充管片与土体之间的空隙，保证管片早期及后期的稳定性；控制地表变形、提高管片的防渗性[11]。为分析壁后注浆层材料参数及土体与衬砌接触非线性对管片动力响应的影响，设置以下3 种工况。

工况Ⅰ：注浆层材料参数采用注浆层实际参数，考虑管片与土体接触面的相对滑移与分离。

工况Ⅱ：将注浆层材料参数提高至与管片材料参数相同，其余与工况Ⅰ相同。

工况Ⅲ：衬砌节点与注浆层节点位移耦合，不考虑管片与土体间的相对滑移及分离，其余与工况Ⅰ相同。

选取轴力及弯矩的控制单元作为监测单元进行不同工况下管片接头动力性能的对比。

5.2 各计算工况下节点相对位移

选择以下位移监测节点：拱顶外侧节点4989、拱底外侧节点3918、左拱腰外侧节点5802、右侧拱腰外侧节点14788。水平相对位移监测节点取5802、14788，竖向相对位移监测节点取4989、3918。各计算工况下节点相对位移见表2。

表2 不同工况下监测节点相对位移 Table 2 Relative displacements between monitoring nodes under different conditions

上述结果表明，管片与土体的接触非线性对管片节点相对位移影响较大；提高注浆层材料强度，管片监测节点间相对位移减小。

5.3 各计算工况下管片接头轴力与弯矩

选择管片一环内接头单元作为监测单元，分析不同工况下管片接头的动力反应。不同工况下接头轴力及弯矩见表3。

表3 不同工况下接头轴力及弯矩 Table 3 Axial forces and moments of segment connector under different conditions

上述结果表明，注浆材料强度的提高，管片接头轴力、剪力及弯矩减小；不考虑管片衬砌与土体间的接触非线性，接头轴力、剪力、弯矩明显减小。管片与土体的接触非线性对管片接头轴力、剪力及弯矩影响较大，

5.4 管片-土体接触非线性对管片动力响应的影响

考虑管片与土体间接触非线性后，管片受土体的约束作用变小，地震荷载作用下管片与土体发生了切向相对滑移和法向分离现象，管片之间在连接处的相对变形增大。管片轴力（见图11，12）、弯矩（见图13）、位移及接头轴力与弯矩（见表3）均明显变大，因此，在地震荷载，尤其在强震作用下考虑管片与土体的接触非线性是必要的。

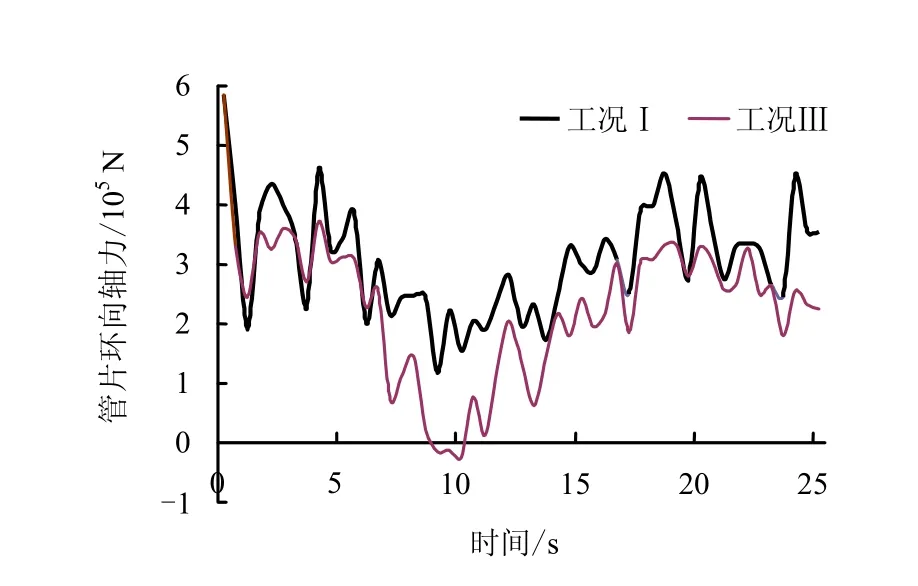
图11 管片监测单元环向轴力时程曲线 Fig.11 Axial force history curves of monitoring element in circumferential direction of case I and III

图12 管片监测单元厚度方向轴力时程曲线 Fig.12 Axial force history curves of monitoring element in thickness direction of case I and III

图13 管片监测单元环向弯矩时程曲线 Fig.13 Moment history curves of monitoring element in circumferential direction of case I and III

5.5 注浆层材料参数对管片动力响应的影响

隧道注浆层材料强度的提高，注浆层对管片变形的约束增强，管片的整体性增强，管片轴力（见图14，图15）、弯矩（见图16）及节点位移（见表2）均有所降低，接头内力（见表3）明显减小。事实上，提高注浆层参数在一定程度上相当于增加了衬砌厚度，从而验证了软土地层中设置抗震层的抗震效果。

因此，在保证注浆层活易性、流动性及填充度的前提下，通过改良注浆材料，适当提高注浆层的强度、黏聚力等措施不仅可以增强其防渗性及管片前期的稳定性，还将有利于提高隧道的抗震性能。

图14 管片监测单元环向轴力时程曲线 Fig.14 Axial force history curves of monitoring element in circumferential direction of case I and II

图15 管片监测单元厚度方向轴力时程曲线 Fig.15 Axial force history curves of monitoring element in thickness direction of case I and II

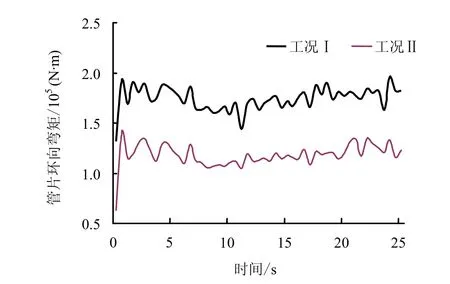
图16 管片监测单元环向弯矩时程曲线 Fig.16 Moment history curves of monitoring element in circumferential direction of case I and II

6 结 论

（1）厚壳-接触-无限元动力分析模型及相应的计算方法可以考虑盾构隧道管片的非连续性、管片接头及错缝连接，可模拟管片间及管片与围岩间复杂的相互作用，工程实例分析结果与地震观测资料对比表明，该计算模型可反映盾构隧道管片、接头在地震荷载作用下受力破坏特征，可用于隧道洞口段、典型横断面及隧道纵向抗震分析，对于研究盾构或TBM 施工隧道的震害分析具有很好的推广价值。

（2）提高壁后注浆层材料强度及土体与衬砌间的切向摩擦力可有效降低管片内力、位移及接头内力；土体与管片的接触非线性对管片、接头动力性能影响较大，在隧道穿越抗震不利地层时，盾构隧道抗震分析需考虑管片与土体间接触面的非线性。

（3）对软土地层中的盾构隧道而言，适当提高注浆层材料参数及注浆层厚度，增加土体与管片间的黏结力，减小管片与土体之间的相对滑动；在管片连接处合理设置弹性垫片、止水橡胶等措施缓解管片及接头应力集中，将有利于提高盾构隧道抗震性能。

[1] 小泉淳. 盾构隧道的抗震研究及算例[M]. 北京: 中国建筑工业出版社, 2009.

[2] 侯公羽, 杨悦, 刘波. 盾构管片接头模型的改进及管片内力的数值计算[J]. 岩石力学与工程学报, 2007, 26 (增刊2): 4284－4286. HOU Gong-yu, YANG Yue, LIU Bo. Improved joint model of shield tunnel segments and numerical calculation of inner forces[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(Supp.2): 4284－4286.

[3] 官林星, 朱合华, 于宁. 考虑荷载工况组合的盾构衬砌横向受力分析[J]. 岩土力学, 2004, 25(8): 1302－1306. GUAN Lin-xing, ZHU He-hua, YU Ning. Analysis of internal force of shield lining in cross-section considering load combination[J]. Rock and Soil Mechanics, 2004, 25(8): 1302－1306.

[4] 张建刚, 何川, 杨征. 大断面宽幅盾构管片三维内力分布分析[J]. 岩土力学, 2009, 30(7): 2058－2062. ZHANG Jian-gang, HE Chuan, YANG Zheng. Analysis of 3D internal forces distribution of wide segment lining for large-section shield tunnel[J]. Rock and Soil Mechanics, 2009, 30(7): 2058－2062.

[5] 张建刚, 何川, 杨征. 武汉长江隧道管片衬砌结构受幅宽影响的力学分布特征研究[J]. 岩石力学与工程学报, 2007, 26(增刊2): 3764－3768. ZHANG Jian-gang, HE Chuan, YANG Zheng. Study of mechanical distribution characteristic of lining structure influenced by segment width for Wuhan Yangtze River tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(Supp.2): 3764－3768.

[6] CHOI JUN SEONG, LEE JONG SEH, MEMBER ASCE, et al. Nonlinear earthquake response analysis of 2-D underground structures with soil-structure interaction including separation and sliding at interface[C]//15th ASCE Engineering Mechanic conference. New York: Columbia, 2002: 1－8.

[7] 苏宗贤, 何川. 盾构隧道管片衬砌内力分析的壳-弹簧-接触模型及其应用[J]. 工程力学, 2007, 24(10): 131－136. SU Zong-xian, HE Chuan. Shell-spring-contact model for shield tunnel segmental lining analysis and its application[J]. Engineering Mechanics, 2007, 24(10): 131－136.

[8] 周维垣. 高等岩石力学[M]. 北京: 水利电力出版社, 1990.

[9] 黄胜, 陈卫忠, 杨建平. 地下工程地震动力响应及抗震研究[J]. 岩石力学与工程学报, 2009, 28(3): 483－490. HUANG Sheng, CHEN Wei-zhong, YANG Jian-ping, et al. Research on earthquake-induced dynamic responses and aseismic measures for underground engineering[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(3): 0483－0490.

[10] 中华人民共和国住房与城乡建设部. GB 50011－2010 建筑抗震设计规范[S]. 北京: 中国建筑工业出版社, 2010.

[11] 罗超红, 付亚伟. 盾构壁后充填注浆材料分析[J]. 公路与汽运, 2007, (5): 176－178.