锦屏深埋大理岩破裂扩展的时间效应 试验及特征研究
刘 宁,张春生,褚卫江
(中国水电顾问集团 华东勘测设计研究院,杭州 310014)
1 引 言
脆性岩石的时间效应具体到锦屏大理岩的时间效应是指锦屏大理岩在深埋洞段,当应力达到一定临界值而表现出的破裂随时间不断扩展,导致强度随时间的延长而弱化的行为。破裂发展往往发生在应力水平低于围岩峰值强度,甚至处于弹性状态的情况下。而这种力学行为最终将导致锚杆可能承受过高的荷载,出现大面积锚杆应力超限、破坏深度的不断扩展影响浅部围压的完整性,进而影响其承载力。由此可见,这种破裂随时间扩展的现象将影响引水隧道的安全运行,并且还将不断恶化,破裂扩展的时间效应作为岩石的重要力学特性之一,与地下工程的长期稳定性与安全性紧密相关。很多岩石工程所显露出来的问题往往都是与破裂扩展的时间效应密切相关[1-3]。
图1 为锦屏二级4#引水隧洞滞后掌子面数公里进行的落底开挖中揭露的围岩在经历1.5 a 以上时间以后的破裂情况,肉眼可见的破裂深度达到 60 cm 乃至更深。而对隧洞掌子面推进过程中发生的围岩破坏现象进行的现场编录和统计,掌子面后方的应力型破坏深度一般不大,多为20 cm 的量级水平。显然破裂在长时间的高地应力的作用发生了扩展,而这种严重破裂现象在现场普遍存在,并不是个别现象,说明了破裂随时间发展的特征。

图1 边墙围岩破裂情况 Fig.1 Failure state of surrounding rock
目前关于脆性岩石的破坏研究的出发点主要是岩石强度问题。加拿大URL 在20 世纪90 年代针对Lac du Bonnet 花岗岩强度进行了系统地试验研究,确定岩石的起裂强度ciσ 和损伤强度cdσ ,通过起裂强度和损伤强度来描述岩石的破裂特性[4-5]。Fairhurst[6]在总结了URL 的相关研究成果以后,指出了荷载-变形-时间三轴关系图,其中纵轴为荷载,2 条横轴中的1 条为变形,荷载-变形关系构成了传统的岩体本构关系。在三轴图中还存在1 条轴线,即时间轴,它显示岩体的荷载-变形关系不是一成不变,而是随时间变化,即岩体特性随时间变化。美国能源局在Yucca Mountain 地下试验室,对强度衰减时间效应进行了全面的分析,而对强度时间效应的数值预测和研究主要建立在“等效”基础上,假设强度参数凝聚力c 和摩擦系数f 随时间衰减[7-8]。Schmidtke 等[9]分析了花岗岩和岩浆岩在核废料储存中长期的力学行为。在长期加载过程中,2 种岩石都受到长期荷载的影响。它们的强度大约能够降低到60%的瞬时强度,持续时间从几秒到数十天。
关于岩石破坏的时效特性研究通常是利用流变试验来实现的,到目前为止,人们进行了大量的试验研究,并取得了丰硕的成果[10-11]。然而这些试验多集中在流变性能显著的软弱岩石上,对于脆性岩石的试验研究成果还不多见。然而随着工程规模的增大以及工程所处环境的变化,有关脆性岩石破裂是时效特性引起的工程问题愈加突出,对脆性岩石破裂的时间效应的研究已是迫在眉睫。
2 工程概况
锦屏二级水电站工程中的4 条引水隧洞是迄今为止中国岩石工程建设中埋深最大的地下工程,一般埋深为1 500~2 000 m,最大埋深达到2 525 m,因此,锦屏工程不同于其他地下工程最显著的特点是深埋、高地应力,工程区实测地应力成果显示,实测最大主应力值达42.11 MPa,工程招标设计阶段地应力反演结果表明,引水隧洞轴线剖面上最大主应力值约为70 MPa,在如此高的地应力条件下,大理岩所表现出来的宏观力学特性与常规应力条件下相比具有显著不同的特点。
锦屏二级引水隧洞从东端到西端隧洞沿线经历的地层岩性分别为三叠系中统盐塘组大理岩、中统白山组大理岩、和下统不同岩性组成的地层(见图2)。根据2 条辅助洞揭露的情况,不同时代的大理岩性状存在一定差别,其中盐塘组大理岩具备出现脆性特征和剧烈型破坏的介质条件,而白山组大理岩具有更好的完整性和脆性特征,两者之间的主要差别之一是岩体内节理的发育程度,包括传统概念的宏观节理和长度在数十厘米以内的隐性小节理,所谓隐性是指这些节理只有在深埋条件受到高应力作用出现破损以后才可能被观察到,这也是盐塘组大理岩强度低于白山组大理岩的主要原因之一。
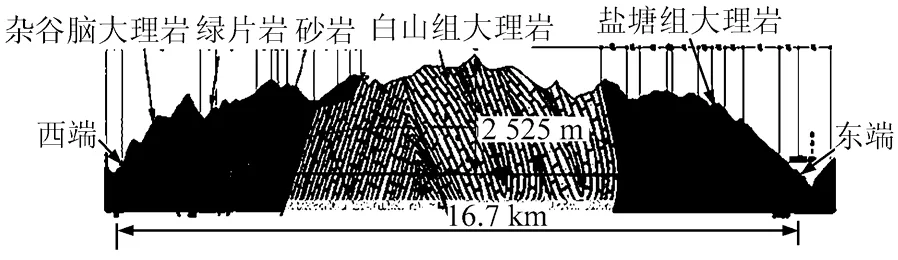
图2 隧洞沿线简化地质剖面图[12] Fig.2 Simplified geological profile along tunnel[12]
3 试验方案
3.1 试验条件
本次试验是在长江水利委员会长江科学院岩土力学与工程水利部重点试验室RW-2000 系列岩石伺服三轴蠕变试验机上完成的,该蠕变试验机可以实现岩石在三轴等环境下的多种试验,控制系统采用全数字伺服控制器。可以同时显示试验力、位移、变形(轴向、径向)、围压、控制方式、加载速率等多种试验和测量参数以及多种试验曲线。根据现场条件,破裂随时间扩展的现象多出现在边墙附近,围压较低,因此,本次试验为单轴长期加载试验。
由于本次试验对岩样的要求较高,对裂纹的存在和扩展比较敏感,加上锦屏的高地应力,在取样过程中很可能对岩样造成初始损伤,进而影响试验结果,因此,本次试验的岩样为采用无损取样技术(见图3)在锦屏二级2-1#试验洞中获得的盐塘组大理岩,无损取样技术可以通过取芯孔周边的应力解除孔来实现对取芯孔的应力解除,避免由于高地应力突然卸载而对岩样产生初始损伤。在进行长期加载试验前期,对取样进行了单轴压缩声发射无损检测,见图4。损伤样在压缩前期声发射信号激增,证明了初始损伤的存在,而利用无损取样技术获得的岩芯前期则比较平静,基本剔除了由于卸荷对岩芯造成的初始损伤,保证了后期试验结果的准确性。
3.2 试验步骤
本次大理岩破裂的时间效应试验是通过一系列的长期加载的静态疲劳试验来完成的,在试验过程中严格按照以下步骤来实施:
(1)首先将无损样套钻成φ 50 mm×100 mm,测量每个岩样的尺寸和声波速度,将声波速度明显偏低的和岩样表面有可见裂隙的排除;
(2)加载过程分为初始加载阶段和稳定加载阶段,初始加载阶段按照位移加载,速率控制在10 mm/min,当到达预先设计的应力值时,停止加载直至破坏;
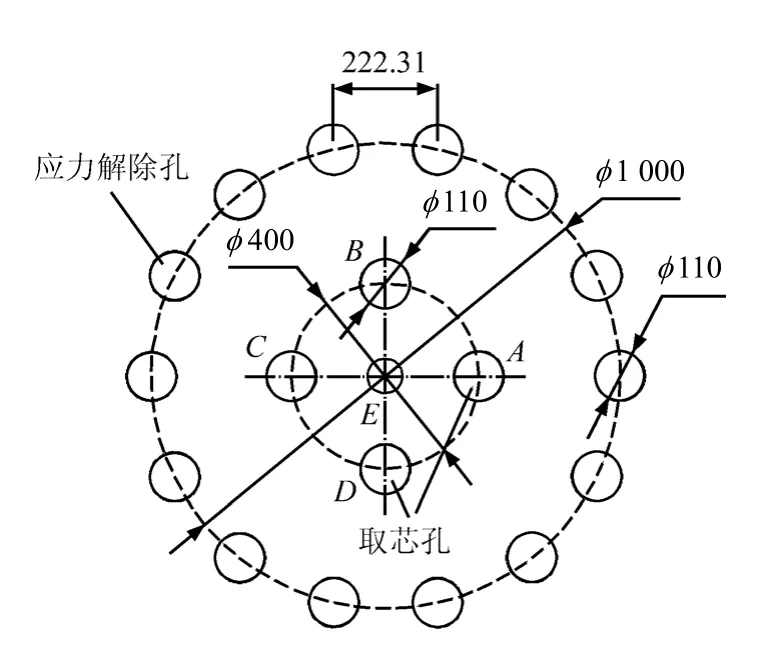
图3 应力解除孔及取芯孔平面布置图(单位:mm) Fig.3 Layout of stress relief and coring holes (unit: mm)
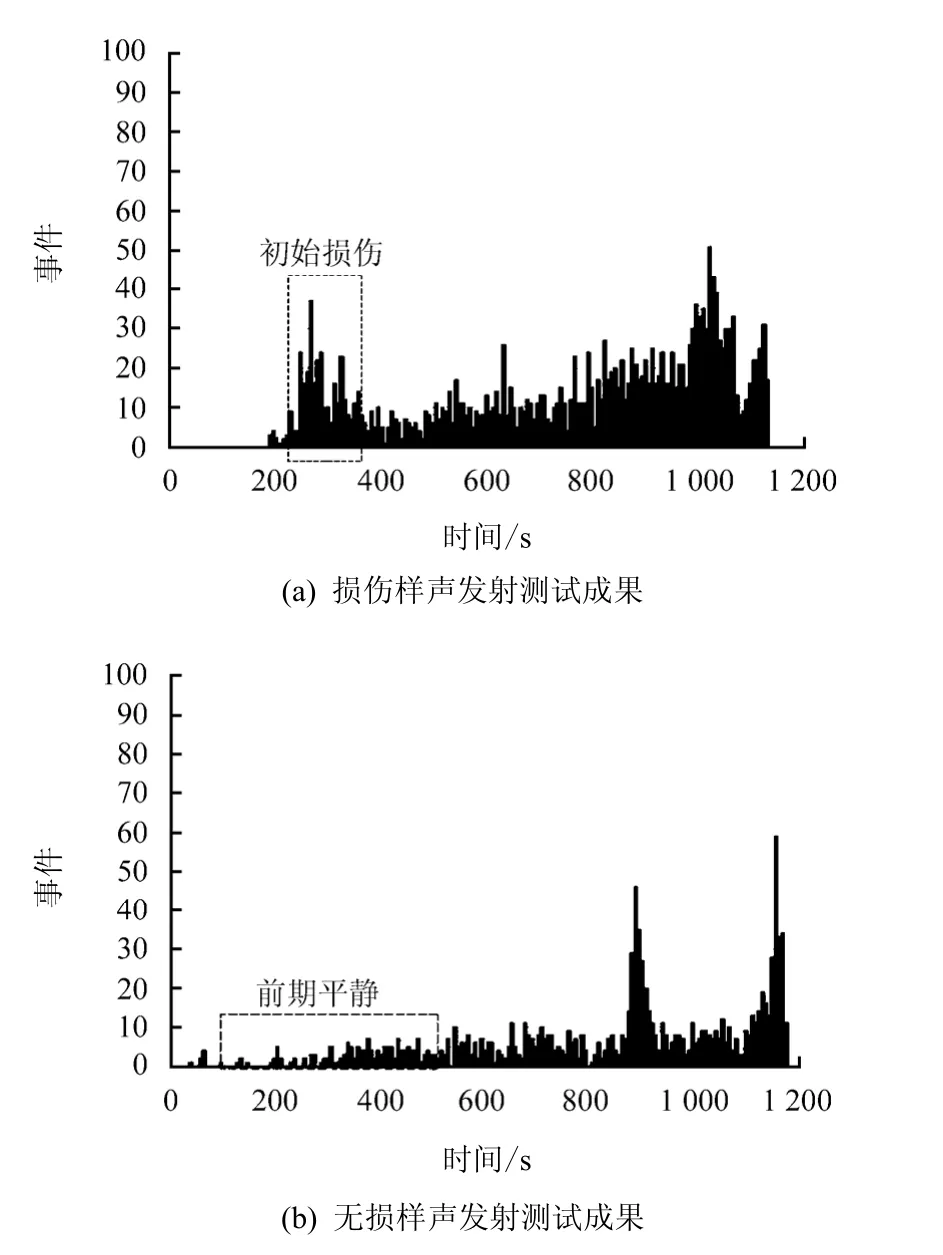
图4 单轴压缩过程中监测到的声发射事件 Fig.4 AE events in uniaxial compression test
(3)施加的长期应力作用从高应力向低应力逐渐过渡,以保证在有限的时间内获得更多地可用数据;
(4)本次试验长期加载的时间最长定为10 d,如果10 d 没有破坏则停止加载;
(5)试验完成后,取出岩样,记录并描述其破坏形式,整理试验数据。
4 试验结果
为了对比数据,时间破坏曲线纵坐标采用破坏时间 tf的对数,而横坐标采用应力驱动比,σ σc= (σ1- Pc) (σf- Pc)。σ1为静态疲劳试验中轴向方向施加的应力; Pc为施加的围压水平,本次试验为单轴压缩试验,因此, Pc= 0;σf为常规压缩试验中测得的峰值强度,通过前期波速相近的岩样进行常规单轴压缩试验来确定,大约为100 MPa,弹性模量为62 GPa,泊松比为0.28;σ 为静态疲劳试验中的偏应力,即 σ = σ1- Pc; σc为常规压缩试验中的偏应力,即 σc= σf- Pc。
将锦屏盐塘组大理岩的静态疲劳数据进行线性拟合,最后得到的结果如图5 所示,相关系数达到0.868 7。如果将破坏需要无限长时间的驱动应力比称为驱动应力比峰值 (σ / σc)th,也可以称作静态疲劳极限,用指数函数来进行拟合,如图6 所示,指数函数无限趋近于0.48,根据已经完成的锦屏盐塘组大理岩的单轴压缩试验成果[13],这个比值介于起裂强度( σci≈ 0.4σc)和损伤强度( σcd≈0.8σc)之间。

图5 盐塘组大理岩(T2y5)静态疲劳试验结果 Fig.5 Static-fatigue test result of Jinping T2y5 marble
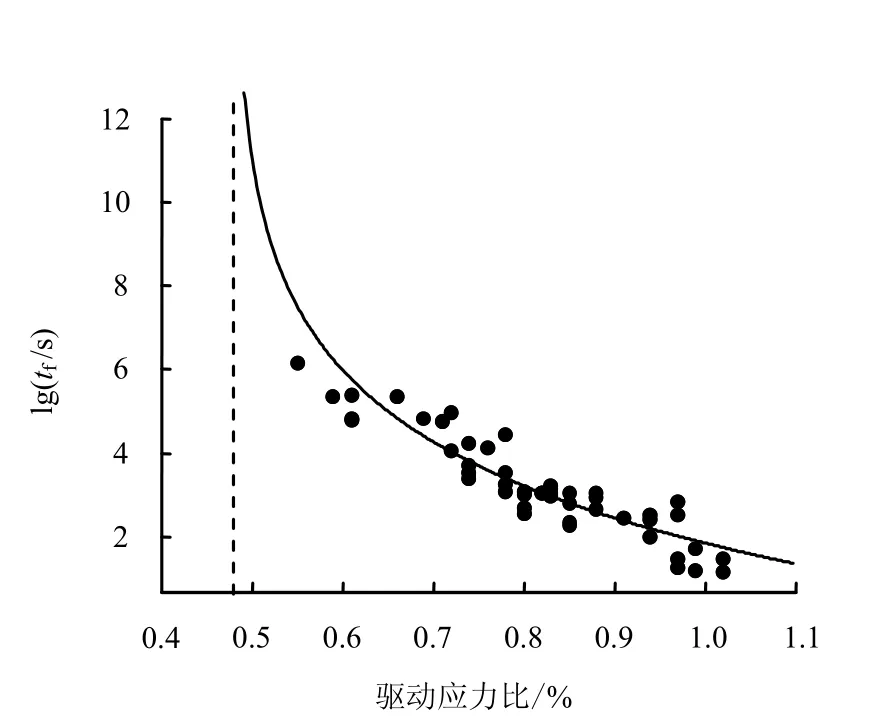
图6 盐塘组大理岩(T2y5)静态疲劳极限 Fig.6 Static-fatigue limit of Jinping T2y5 marble
5 特征分析
5.1 蠕变特征
当岩石在恒定荷载持续作用下,应变可以分为3 个阶段,这3 个阶段分别对应初始蠕变阶段、稳定蠕变阶段和加速蠕变阶段。蠕变过程是应变的增长和恢复相互竞争的结果[14]。在蠕变的第1 阶段,随着应力的增加,应变增长占主导。随着时间的增长,应变速率逐渐降低。如果应力保持不变,应变率会最终维持在一个数值保持不变。应变的增长和恢复保持平衡。这个阶段便是第2 阶段。而第3 阶段即加速蠕变阶段是由于岩石本身持续增加的破坏而引起的应变率增长导致扩容的阶段。在图7 中是本次试验中测得的典型的 蠕变曲线数据。典型的应变率变化过程见图8,可以看出,在第1 阶段应变率单调减少,直到最小值。在稳定蠕变阶段体积基本保持不变。在加速蠕变阶段应变率快速上升直到岩样破坏。
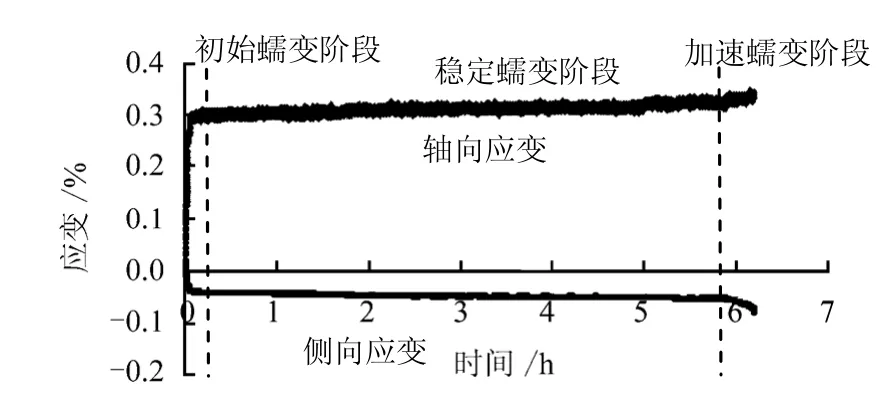
图7 长期荷载作用下的变形的3 阶段 Fig.7 Three stages of deformation under long-term loading

图8 轴向应变率变化 Fig.8 Axial strain ratio change
但对于脆性岩石,特别是有含有结构面的岩样,第3 阶段有时很难被准确地测量出来,当到达第3阶段时很多岩样在极短的时间内便迅速破坏,甚至没有出现明显的第3 阶段便破坏。例如在图9 中的蠕变曲线初始阶段很短,蠕变阶段近似线性增加的不明显,第3 蠕变阶段最终导致试样的破坏。这个行为暗示了变形与时间相关性,并与在恒定压应力作用下的裂纹扩展密切相关。当裂缝密度达到临界值时第3 阶段蠕变开始。同时侧向应变比轴向应变表现出更大的时间相关性,表明在恒定荷载作用下膨胀和裂缝的贯通。
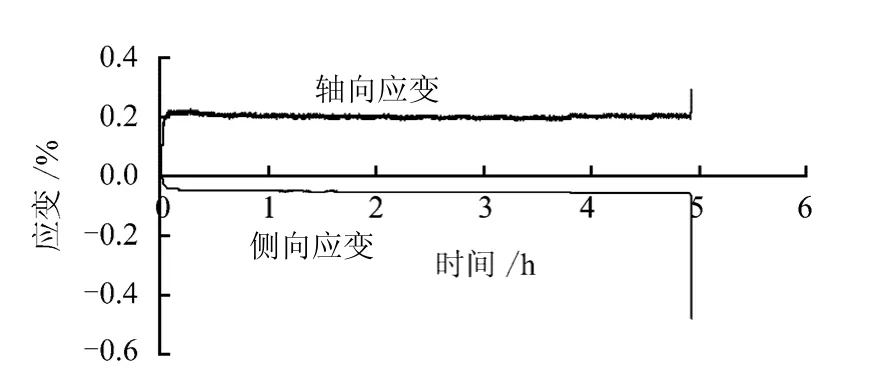
图9 长期加载过程中的蠕变曲线 Fig.9 Creep curves under long-term loading
5.2 扩容特征
岩石在长期荷载下的变形对扩容有重要影响,进而影响岩石的渗透性。大量的试验已经证明,岩石的破坏严重依赖于时间。岩石的破裂归因于大量新生裂纹的逐步形成或者已有裂纹的扩展。扩容便是这样产生的。岩石的破坏便开始于扩容的增加。Schock[15]发现,岩石破裂之前都是以扩容作为标志的,而其增加的应变比 -τ σ 曲线更好地预测岩石的破坏,因为增加的剪切应变直接与破坏有关。Kurita等[16]研究了Westerly 花岗岩的变形,发现破裂面形成于蠕变的第3 阶段。
扩容是脆性岩石的重要的特征。在本文的研究中,扩容定义为施加不同应力产生的微裂纹扩展导致的非弹性体积应变。蠕变变形是由弹性变形和非弹性变形组成的。假设弹性模量在整个试验过程中保持不变,根据虎克定律,非弹性剪切应变可以表示为

非弹性体积应变可以表示为
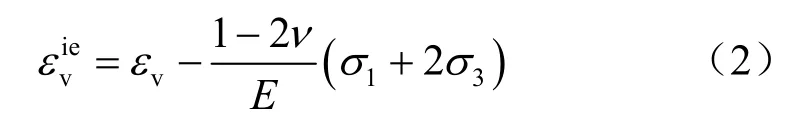
在单轴情况下,30σ =

图11 对比了2 种加载应力条件下的扩容指标,当应力比增加时,扩容指标有微小的下降。原因是越高的应力比会导致更大的非弹性剪切应变的增长,这也导致扩容指标DI 的下降。
5.3 破坏特征
深埋大理岩的破坏模式受内部细观结构的控制。当岩样完整性好,强度较高时,以剪切破坏为主。而在静态疲劳试验中不变荷载部分产生的应变趋向于非弹性和不可恢复,这点已经在前面的分析中说明,其中增加的体积应变意味着轴向裂纹的扩展,剪切应变的增长意味着剪切滑移。两种破坏模式相互交结。在此试验过程中岩石破坏在沿轴向的微裂纹扩展和沿倾斜裂纹的剪切滑移都表现的比较明显(见图12)。由于在试验过程中不能迅速停止,出现了整个的剪切破坏。然而近距离观察可以发现大量的近似平行的轴向裂纹。
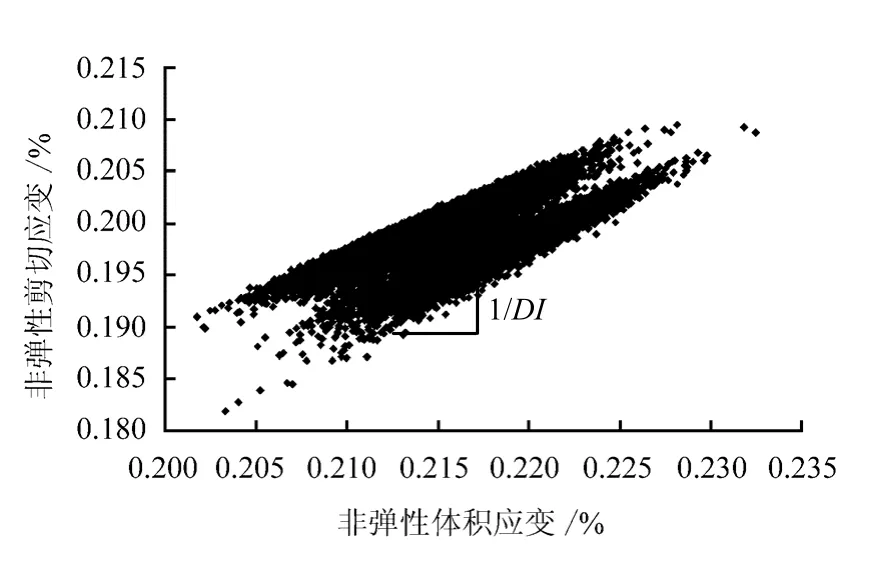
图10 蠕变过程中的扩容指标 Fig.10 Dilatancy index in creep process

图11 不同应力条件下的扩容指标 Fig.11 Dilatancy index under different loadings

图12 破坏岩样(包含宏观剪切面和轴向裂纹) Fig.12 Failure rock samples including macroscopic shear surfaces and axial cracks
6 影响因素分析
6.1 埋深的影响
锦屏工程的显著特点是高埋深、高地应力。这也导致其围岩的力学性质明显区别于浅埋工程。本次试验的取样地点的埋深超过1 900 m,这也导致在取样过程中对岩芯的损伤,虽然前期经过了无损取样和套钻,但在试验过程中强度仍然表现出来比较大的离散性,部分岩样在初始加载过程中便发生破坏,其中埋深是一个不可忽视的因素。为了更进一步分析取样的深度对岩样的损伤,建立了FLAC3D模型对此进行了简单评估。从图13 中可以看出,如果取芯深度超过10 m,避开应力松弛区和应力集中区,那岩芯的完整性会更好。图14 中整理了最后完成静态疲劳试验的岩样埋深的分布情况,可以看出埋深基本都超过了10 m,说明埋深对岩样强度的影响确实存在。
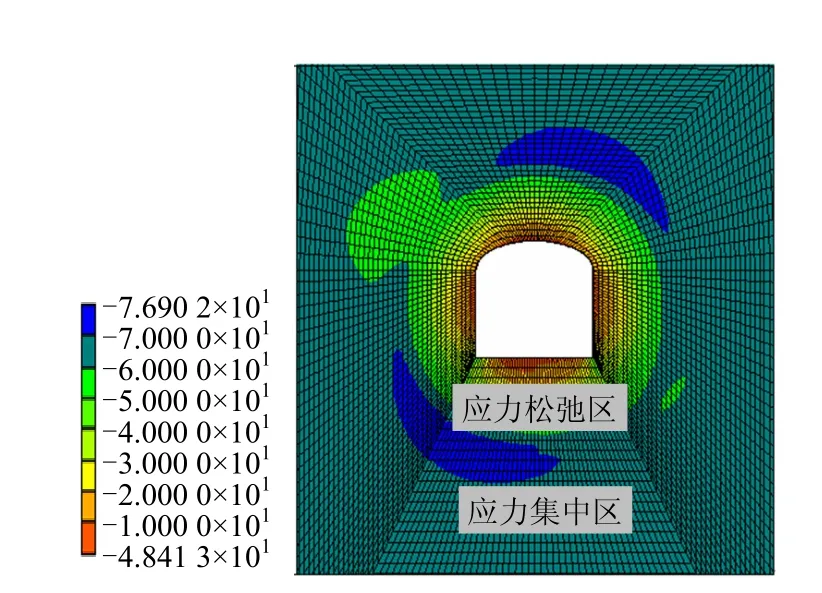
图13 试验洞开挖后的最大主应力云图 Fig.13 Maximum principal stress contour after test tunnel excavated
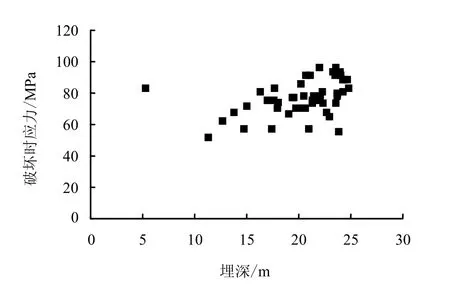
图14 可利用数据与埋深、应力的关系 Fog.14 The relation among available data, depth and stress
6.2 节理的影响
锦屏白山组大理岩和盐塘组大理岩的主要区别之一就是节理的发育程度,尤其是隐形节理,这些节理的存在影响了盐塘组大理岩的强度,在本次试验中,岩样的强度同样也受到其影响,强度明显小于完整的试样,导致在初始加载过程中多次出现破坏现象。
如何模拟节理对岩石强度的影响,一直是岩石力学的难点,而基于颗粒流程序PFC 建立的等效岩体技术能够比较充分地反映结构面的分布特征,并能够考虑细观破裂效应。该项技术主要包括黏结颗粒模型、结构面模型以及相应的加、卸载方式。其中黏结颗粒模型是由Potyondy 等[18]提出并创建的,主要用于模拟完整岩块在外荷载作用下的变形、破坏等力学特性;而结构面模型主要用于模拟岩体结构面的构造。在结构面网络模型中,主要由光滑节理模型来表示[19]。
根据含节理岩样的产状和长度(见图15),建立了如图16 所示的模型,可以看出由于节理的存在,对岩样的整体强度有很大的影响,单轴强度仅有44.7 MPa,远远低于前期完成的单轴试验中测到的强度。在节理和上部端面交结处都出现了应力集中现象,并产生了剪裂纹,最终导致岩样的边缘出现破坏。
同时节理的存在对应力-应变曲线的形状也产生了一定的影响,在加载初期,应力迅速上升1~ 2 MPa,将岩样和节理之间的空隙压缩紧密,而在残余阶段,存在一定的强化效应和延性特征,主要是结构面的摩擦力在起作用。

图15 含节理岩样实测应力-应变曲线 Fig.15 Stress-strain curve of jointed rock

图16 PFC 模拟的应力应变曲线和破裂形态 Fig.16 Stress-strain curve and failure mode simulated by PFC
7 结 论
(1)试验结果表明,在稳定荷载作用下脆性岩石的强度会逐渐降低直至破坏。当应力驱动比较低时,需要的时间也相应增加。应力驱动比可以利用指数函数很好地回归,最终得到的驱动比疲劳极限是0.48。
(2)当脆性岩石在稳定荷载作用下,蠕变曲线可以分为3 个阶段:初始蠕变阶段(第1 阶段)、稳定蠕变阶段(第2 阶段)、加速蠕变阶段(第3 阶段)。在第1 阶段应变率单调减少,直到最小值,在稳定蠕变阶段体积基本保持不变,在加速蠕变阶段应变率快速上升直到岩样破坏,而侧向应变比轴向应变表现出更大的时间相关性。
(3)通过扩容指标分析了在稳定荷载作用下应变的变化过程。其中非弹性剪切应变和非弹性体积应变之比近似线性。这个比值意味着剪应变和体积应变同时发生。而且这些应变的相对称部分在不稳定裂纹扩展过程中保持不变。
(4)静态疲劳试验中不变荷载部分产生的应变趋向于非弹性和不可恢复,其中增加的体积应变意味着轴向裂纹的扩展,剪切应变的增长意味着剪切滑移。两种破坏模式相互交结。在此试验过程中岩石破坏在沿轴向的微裂纹扩展和沿倾斜裂纹的剪切滑移都表现的比较明显。
(5)岩芯的埋深对本身的强度影响也比较明 显,本次试验可利用数据埋深基本上都超过了10 m,避开了由于隧洞开挖引起的应力松弛区和应力集中区的范围。
(6)利用PFC 中的平滑节理模型模拟了节理对岩样强度的影响,与试验中的现象一致,节理的存在极大地影响了岩样的整体强度,在加载初期,存在压缩紧密,而在残余阶段,存在一定的强化效应和延性特征。
[1] 孙钧. 岩土材料流变及其工程应用[M]. 北京: 中国建筑工业出版社, 1999.
[2] 孙钧. 岩石非线性流变特性及在地下结构工程中的应用研究[R]. 上海: 同济大学地下工程系, 1990.
[3] LI YONGSHENG, XIA CAICHU. Time-dependent tests on intact rocks in uniaxial compression[J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 2000, 37(3): 467-475.
[4] READ R S. 20 Years of excavation response studies at AECL's underground research laboratory[J]. International Journal of Rock Mechanics and Mining Sciences, 2004, 41(8): 1251-1275.
[5] CAI M, KAISERP K, TASAKA Y, et al. Generalized crack initiation and crack damage stress thresholds of brittle rock masses near underground excavations[J]. International Journal of Rock Mechanics and Mining Sciences, 2004, 41(5): 833-847.
[6] FAIRHURST C. Nuclear waste disposal and rock mechanics: contributions of the underground research laboratory (URL), Pinawa, Manitoba, Canada[J]. International Journal of Rock Mechanics and Mining Sciences, 2004, 41(8): 1221-1227.
[7] LIN M, KICKER D, DAMJANAC B, et al. Mechanical degradation of emplacement drifts at Yucca Mountain—A modeling case study-Part I: Nonlithophysal rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2007, 44(3): 351-367.
[8] LIN M, KICKER D, DAMJANAC B, et al. Mechanical degradation of emplacement drifts at Yucca Mountain—A modeling case study-Part II: Lithophysal rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2007, 44(3): 368-399.
[9] SCHMIDTKE R H, LAJTAI E Z. The long-term strength of Lac du Bonnet granite[J]. International Journal of Rock Mechanics and Mining Sciences, 1985, 22(6): 461-465.
[10] MARANIMI E, BRIGNOLI M. Creep behavior of a weak rock experimental characterization[J]. International Journal of Rock Mechanics and Mining Sciences, 1999, 36(3): 127-138.
[11] 廖红建, 宁春明, 俞茂宏, 等. 软岩的强度-变形-时间之间关系的试验分析[J]. 岩土力学, 1995, 19(2): 8-13. LIAO Hong-jian, NING Chun-ming, YU Mao-hong, et al. Experimental study of strength-deformation-time relationship of soft rock[J]. Rock and Soil Mechanics, 1998, 19(2): 8-13.
[12] 张春生, 陈祥荣, 侯靖, 等. 锦屏二级水电站深埋大理岩力学特性研究[J]. 岩石力学与工程学报, 2010, 29(10): 1999-2009. ZHANG Chun-sheng, CHEN Xiang-rong, HOU Jing, et al. Study of mechanical behavior of deep-buried marble at Jinping II hydropower station[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(10): 1999-2009.
[13] 褚卫江, 刘宁, 房敦敏. 锦屏二级水电站引水隧洞2-1#试验洞原位岩石力学试验及室内试验分析汇总报告[R]. 杭州: 华东勘测设计研究院, 2010.
[14] CRISTESCU N, HUNSCHE U. Time effects in rock mechanics. Series: Material, modelling and computation[M]. New York: Wiley, 1998.
[15] SCHOCK R N. A constitutive relation describing dilatant behavior of Climax Stock granodiorate[J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 1976, 13(7): 221-223.
[16] KURITA K, SWANSON P L, GETTING I C, et al. Surface deformation of westerly granite during creep[J]. Geophysical Research Letters, 1983, 10(1): 75-78.
[ 17] LIN Q X, LIU Y M, THAM L G, et al. Time-dependent strength degradation of granite[J]. International Journal of Rock Mechanics and Mining Sciences, 2009, 46(7): 1103-1114.
[18] POTYONDY D O, CUNDALL P A. A bonded-particle model for rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2004, 41(8): 1329-1364.
[19] IVARS D M, POTYONDY D O, PIERCE M, et al. The smooth-joint contact model[C]//SCHREFLER B A, PEREGO U. Proceedings of the 8th World Congress on Computational Mechanics. Venice: [s. n.], 2008.

