水工隧洞围岩裂纹扩展的临界水压解析解

卞 康，肖 明，胡田清

（1. 中国科学院武汉岩土力学研究所 岩土力学与工程国家重点实验室，武汉 430071； 2. 武汉大学 水资源与水电工程科学国家重点实验室，武汉 430072）

1 引 言

天然岩体中包含各种孔隙、微裂纹以及节理裂隙等不连续面，不仅改变了岩体的物理力学特征，也为地下水提供了在岩体中的储存场所及运移通道。在高水头、高埋深等条件下，高压水会使得岩体裂缝扩展、贯通，产生水力劈裂现象。

水力劈裂在工程中有着重要应用，如作为油气井增产的主要措施应用于原位地应力测量，但同时也可能造成严重的后果甚至工程事故[1]。在高水头作用下，水工隧洞易由于水力劈裂出现涌水事故，甚至出现大量宽度较大、延伸较长的裂缝威胁工程结构的稳定。研究水工隧洞裂纹扩展的发生机制，对有效预防或及时治理隧洞开裂和涌水，维持水工隧洞结构稳定性有着重要的工程意义。

大量试验证明，裂缝在岩体中始终沿着最小阻抗的路径扩展，即裂纹在延伸过程中裂纹面始终垂直于最小主应力方向[1]。Hubbert等[2]在假定岩石是均值各向同性线弹性介质，同时具有脆性和不透水特性的基础上，对水力劈裂引起的张拉开裂和应力场的关系进行了研究。断裂力学理论的引入为水工隧洞裂纹扩展问题的研究提供了有效手段。黄润秋等[3]针对深埋隧洞的涌水问题进行了断裂力学机制分析，推导了水力劈裂发生时的临界水压和裂隙张开度变化公式，但文中对压剪型裂纹的研究中采用纯Ⅱ型裂纹扩展判据，与实际存在一定的差距。在文献[3]的基础上，盛金昌等[4]针对水工隧洞岩壁裂纹对压剪型裂纹的扩展机制做出了进一步探索。另一方面，岩石拉剪和压剪型裂纹扩展规律研究已成为近年来的研究热点问题。李宗利等[5]提出了岩石水力劈裂发生时的临界内水压力表达式。黄达等[6]采用线弹性断裂力学理论和物理模型试验研究了拉剪应力状态下岩体裂隙扩展的力学机制。邓华锋等[7]对考虑裂隙水压力的岩体压剪裂纹扩展规律进行了探索。刘涛影等[8]研究了高渗压条件下压剪岩石裂纹断裂损伤的演化机制。

当前的岩石裂纹扩展机制研究大多局限于岩石裂纹自身的扩展判据研究，与结构（如水工隧洞）整体受力多无关联；同时由于上述原因，在求解临界压力时，需要提供裂纹所在处地应力值，由于地应力值获取的难度，这在很大程度上限制了裂纹扩展公式的应用范围。针对上述不足，本文将断裂力学扩展判据引入水工隧洞解析解中，使宏观的水工隧洞受力与细观的裂纹扩展相结合，将裂纹发生扩展时的隧洞内水压力定义为临界水压，提出了水工隧洞围岩裂纹扩展的临界水压公式，并对裂纹的走向、长度、埋深等参数对临界水压的影响进行了分析。

2 圆形隧洞围岩裂纹扩展机制研究

2.1 隧洞受力分析

本文基于如下假定：

（1）隧洞围岩为均质、各向同性弹脆性材料；

（2）天然岩体介质中存在着非连续裂纹，且裂纹在岩体中随机分布；

（3）裂纹的开展为二维问题，且在垂直于隧洞轴线的平面上扩展。

地下水是岩体重要的初始赋存条件之一，裂隙中的渗透水压力对岩体水力劈裂会产生重要影响，因此，应首先对隧洞渗流场进行相应分析。在隧洞充水后，处在无限大弹脆性岩体介质中的圆形隧洞受力模型如图1 所示。由于岩石为均质各向同性材料，其在各个方向上的渗透系数均相同，因此，可以简化为轴对称平面稳定渗流问题，描述渗流的微分方程和边界条件可以写为[9]

式中：wp 为孔隙水压力；r 为距隧洞中心距离。

设隧洞内半径0r 处的孔隙水压力为mp ，在隧洞半径cR 处以外的渗流场与初始渗流场孔隙水压力ip 相同。结合此边界条件对式（1）求解，隧洞充水后的围岩孔隙水压力表示为[9]

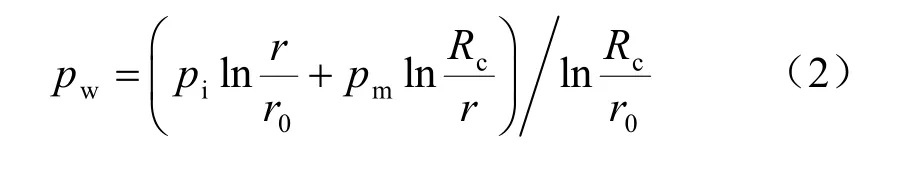
图1 圆形水工隧洞受力示意图 Fig.1 Load-bearing of circular hydraulic tunnel

如图1 所示，由于围岩为弹脆性材料，隧洞充水后围岩可视为受内水压力0p 、无限远处初始地应力q 共同作用下的弹性厚壁圆筒，围岩应力表达式可根据Lame 解答[10]写为

式中：rσ′和θσ′ 分别为隧洞围岩的径向应力和切向应力。

由于围岩中存在孔隙与裂隙，孔隙水必然承担一部分应力，因此，通过岩石颗粒接触面传递的应力，即有效应力，才是控制含水岩体强度和变形的状态参量。Terzaghi 提出的有效应力公式[11]，经过大量试验已证明其完全可以在岩石材料中应用。但相对于土而言，由于岩石中的孔隙相对较小且孔隙之间的连通率也较低，孔隙水无法完全弥散于整个岩体的内部，对有效应力公式应根据孔隙水与岩体的接触面积做出修正。由于本文假定以拉为正，以压为负，而土力学中规定以压为正，有效应力公式中孔隙水压力项前负号应做变号处理，因此，考虑孔隙水压力的Lame 解答可以写为

式中：rσ 和θσ 分别为围岩的有效径向应力和有效切向应力；η 为围岩孔隙水的作用面积系数，其值与围岩孔隙率等因素有关，在0～1 之间，可以通过试验确定。

2.2 拉剪裂纹受力分析

对于隧洞围岩的水力劈裂现象，基于假定（1），可以采用考虑小范围屈服的线弹性断裂力学理论对裂纹扩展机制进行分析。真实隧洞围岩中的裂纹是三维的，但由于三维问题较为复杂，在实际分析时可以将其考虑为二维裂纹。典型的包含一条闭合裂纹的断裂力学模型如图2 所示。

图2 洞周片状裂纹示意图 Fig.2 Platy crack nearby the tunnel

闭合裂纹长度为2a，裂纹长轴与最大主应力1σ 间的夹角为β ，则裂纹面上的正应力和剪应力分别为[5]

由于裂纹所处的应力状态较为复杂，大部分裂纹均为复合型裂纹。但假定（3）使得裂纹只受平面问题中的正应力和剪应力影响，因此，裂纹为Ⅰ-Ⅱ复合型。根据裂隙壁面是拉应力还是压应力，可以分为拉剪型和压剪型裂纹两种类型。对于拉剪复合型裂纹，考虑到常用复合型裂纹的扩展判据，如最大周向应力准则等计算的繁琐性以及理论与工程实际的差距，本文采用工程常用中的Ⅰ-Ⅱ拉剪复合型裂纹扩展判据：

式中：CKI为Ⅰ型断裂韧度，Ⅰ型和Ⅱ型断裂强度因子KI和KII表达式为

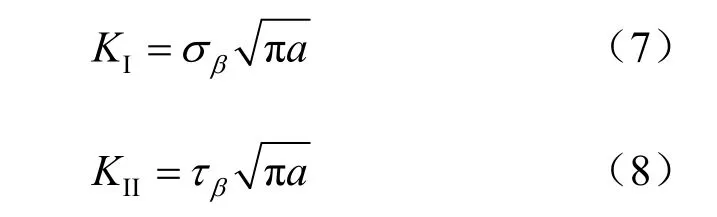
对于拉剪型裂纹，βσ 必须为正值，由式（5）～（8）联立可得

结合式（4）、（9），考虑到 σ1、σ3和 σr、σθ的对应关系，无论 σ1= σr，σ3= σθ还是 σ1=σθ，σ3= σr，均有下式成立：

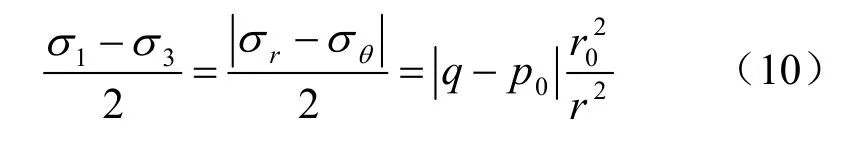
将式（2）、（4）、（10）代入式（9），可得

根据式（11），距离隧洞中心r 处的Ⅰ-Ⅱ拉剪复合型裂纹扩展时的临界内水压力表达式为

2.3 压剪裂纹受力分析

如果裂纹面法向应力为压应力时，裂纹为Ⅰ-Ⅱ压剪复合型。此时的开裂机制与拉剪裂纹扩展完全不同。Erdogan 等[12]认为，在压荷载作用下，岩石中原先存在的粗糙裂纹面将闭合，并形成摩擦阻力，从而阻止裂纹面的相对滑移和初裂扩展。因此，在分析初始断裂条件时，导致裂纹尖端应力奇异性的惟一应力分量是有效剪应力，即对裂纹面施加的名义剪应力减去摩擦阻力后的差值。裂纹面上的摩擦阻力fτ 可以由Mohr-Coulomb 条件得到：

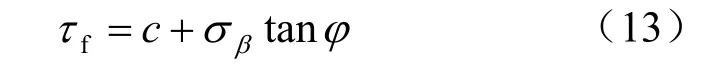
式中：φ 为岩体裂纹面的内摩擦角；c 为裂纹面的凝聚力。

裂纹闭合后，裂纹面上的有效剪应力eτ 对裂纹扩展起控制作用，其表达式为

相应地在压剪断裂过程中的Ⅱ型断裂强度因子KII表达式为

岩石力学试验表明[13]，岩石在压剪试验中，会经历初裂、临界和破坏3 个典型阶段，且在临界点之前裂缝尖端区域会出现扩容现象。由于断裂机制复杂，压剪断裂至今并没有被理论界完全接受的开裂准则。本文采用与试验结果拟合较好的周群力 等[13]提出的压剪断裂判据：

对于压剪型裂纹，βσ 必须为负值，将式（5）、（13）、（14）代入式（15）可得

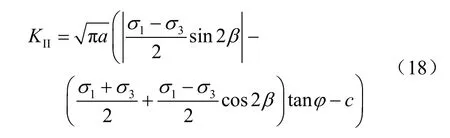
将式（18）、（7）代入式（16），得

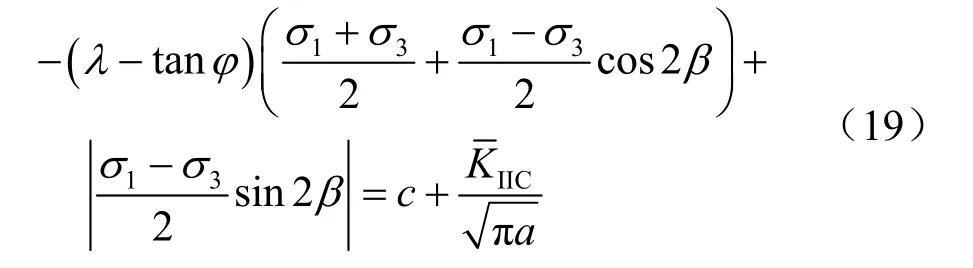
将式（2）、（4）、（10）代入式（19）中，可得

根据式（20），距离隧洞中心r 处的Ⅰ-Ⅱ压剪复合型裂纹扩展时的临界内水压力表达式为

2.4 裂纹扩展分析

不论是拉剪型破坏还是压剪型破坏，每种破坏类型均可求解出两个临界内水压力01p 和02p ，分别对应地应力控制情况和内水压力控制情况。两个临界压力值之间是裂纹稳定区，内水压力在此区间内裂纹不会发生扩展。由于求解的01p 可能大于0 也可能小于0，可以得到裂缝扩展的两种情况，如图3所示。

在第1 种情况中（ p01＞ 0），当 p0＞ p02时，会发生因内水压力过大而导致的裂纹失稳扩展；而当 0 ＜ p0＜ p01时，会发生由于地应力释放而导致的裂纹失稳扩展。对 0 ＜ p0＜ p01的情况而言， p0可以视为支护压力，临界内水压力 p01即可相应视为临界支护压力，即在洞室开挖完成后必须有一定的支护压力来抵消地应力的作用才能使裂纹不致扩展，否则隧洞开挖后，裂纹便处于不稳定状态，只有当裂纹扩展到一定程度后，局部的应力调整使得p01= 0，裂纹才能重新处于稳定状态。

在第2 种情况中（ p01＜ 0），只有当 p0＞ p02时，才会发生因内水压力过大而导致的裂纹失稳扩展，这种情况下实际上只存在一个临界内水压力值。

需要说明的是，临界支护压力01p 只是作为理论研究的对象，用于判别围岩中某条裂纹在隧洞开挖后是否会发生扩展（由01p 的正负决定），且可以确定使其不发生扩展所需的临界支护压力。而在实际工程中，往往更为关心由于内压过大引起的裂纹开展，及其相应的临界内水压力02p ，其值与实际内水压力的相对大小决定了该处围岩是否发生水力劈裂。

图3 不同p01 情况下裂纹开展区示意图 Fig.3 Crack extension zones of different values of p01

由于隧洞围岩中的裂纹随机分布，当研究某一条裂纹扩展的临界压力（临界支护压力或临界内水 压力）时，可以在确定该裂纹的长度、走向及与隧洞中心距离等特征参数后，通过式（12）或（21）求解临界压力，并须同时满足对应裂纹扩展类型对法向应力正负的要求；当裂纹条数很多时，可以在分别求出各条裂纹扩展时的临界压力后，选择其中的最小值作为整个隧洞裂纹扩展的临界压力控制值。

3 算 例

本文采用文献[3]的实例，其中大理岩的Ⅰ型裂纹断裂韧度 KIC=15.2 MN/m1.5，Ⅱ型裂纹断裂韧度=11.2 MN/m1.5，λ=/KIC= 0.736，裂纹面上的内摩擦角φ=45°，凝聚力c=1 MPa，初始地应力q =10 MPa，足够远处的初始渗流水压力 pi= 5 MPa，渗流影响半径 Rc= 30r0，初始裂纹长度a = 2 m。

3.1 裂纹夹角对临界内水压力的影响

为分别研究各参数对临界内水压力的影响，取η =0。首先对裂纹长轴与最大主应力1σ 间的夹角β进行分析，当β 在0°～180°内的典型角度时，临界内水压力值如表1 所示。考虑到在压剪型裂纹临界内水压力公式（21）中， tanλ φ- 的正负号对于最终的结果会产生影响，此时保持λ 值不变，分别令φ=45°、30°，得出相应的 tanλ φ- =-0.264 和0.159，解出对应的临界内水压力值列入表1。

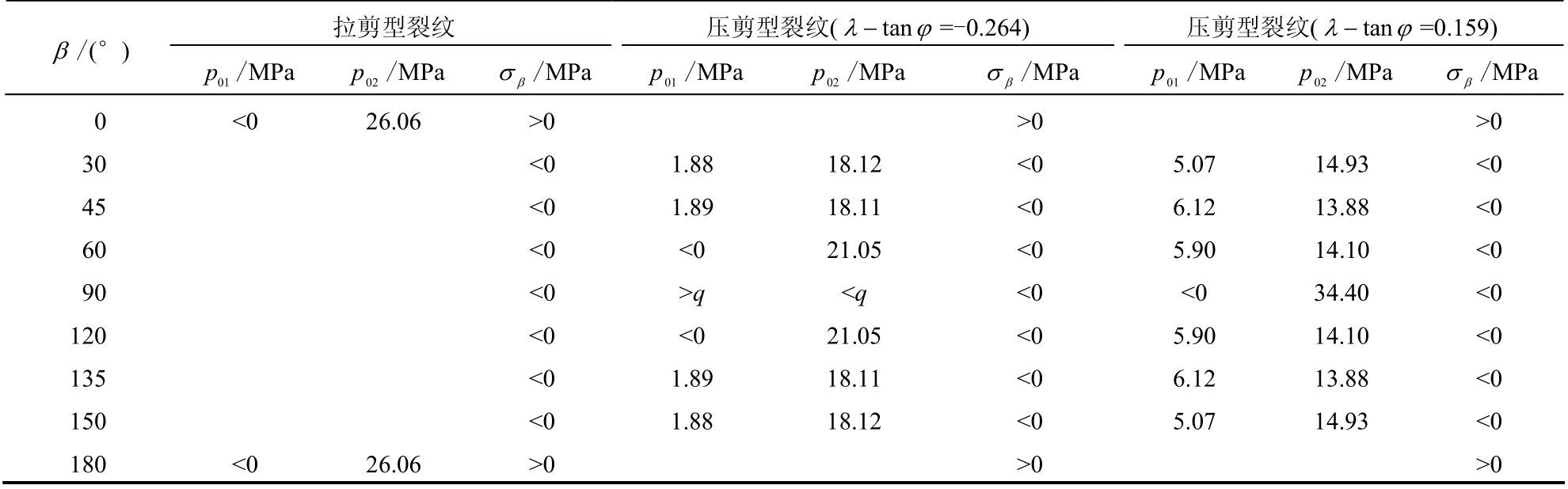
表1 不同β 值对应的临界内水压力 Table 1 Critical inner water pressures with different values of β

由表可见，当λ=-0.264 时，除了当β =0°和180°时，求解出的临界内水压力对应的法向应力为正值外，其余角度法向应力均是负值。可见在该参数条件下，只有在特定角度下(β =0°、180°)，裂纹才会发生拉剪型开展；同理，在β =30°～150°范围内，裂纹均只会产生压剪型开展。在β =60°时，01p ＜0，此时的初始裂纹只有一个临界水压，只有当p0>21.05 MPa 时，裂纹才会因内水压过大发生压剪型开裂。而在β =30°、45°、135°、150°等典型角度时，均对应两个临界内水压力；由于 p01>0，在隧洞开挖完成后这些裂纹是不稳定的，会在扩展后重新达到相应的平衡状态。在β =30°～60°范围内，压剪型裂纹临界水压 p02变幅为18.11～21.05 MPa，变幅相对有限，而拉剪型裂纹对应的 p02则要高于压剪型裂纹。当β 角度互补时，对应的临界内水压力01p 和02p 均相同，可见当裂纹走向与法线交角一定时，均只有确定的临界内水压力值，而与裂纹向哪一侧倾斜无关，这与实际工程规律是符合的。而当β =90°时，01p >q，而02p ＜q，与事前假定不符，可认为在该参数下走向与洞壁法线方向垂直的裂纹不会发生扩展。

比较λ=-0.264 和λ=0.159 对应的临界水压力值，可见压剪型裂纹在不同β 时对应的 βσ 正负号均相同，可见 tanλ φ- 的正负并不会影响裂纹在不同β 值时的开展类型。 tanλ φ- 值对于临界内水压力的影响主要体现在量值上。在λ 从-0.264 变化至0.159 时，01p 均有所增大，而02p 则有所降低。可见在其余参数不变，而围岩内摩擦角减小后，在地应力起控制作用情况下，需要更多的支护压力来抵消地应力的作用才能使裂纹不致扩展；而在内水压力起控制作用情况下，需要更小的临界内水压力就可以使得裂纹因内水压力过大而开展。因此，围岩内摩擦角的减小对于隧洞维持稳定是不利的，这与维持裂纹稳定的内水压力区间变小有直接联系。在β =90°、λ=0.159 时，出现对应的临界内水压力为34.40 MPa，可见当围岩内摩擦角减小后，原先不能发生扩展的裂纹也有可能发生压剪型开裂，但对应的临界内水压要显著高于β 为其他角度的情况。可见β =90°时对应的裂纹最为稳定，扩展的可能性比其他夹角情况下要小得多。

3.2 初始裂纹长度对临界水压力的影响

为研究初始裂纹长度a 对于临界水压力值的影响，分别对a 取0.1～5 m 范围内的值，当β =30°、β =60°时，压剪型裂纹02p 与a 关系曲线分别如图4、5 所示。

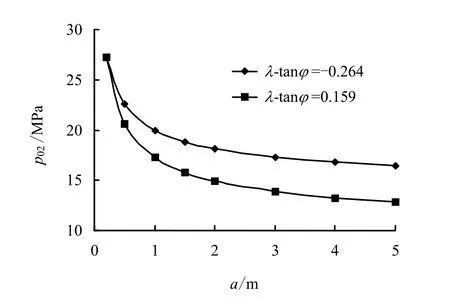
图4 压剪型裂纹p02 与a 关系曲线(β =30°) Fig.4 Relationships between p02 and a of shear-compression crack (β =30°)

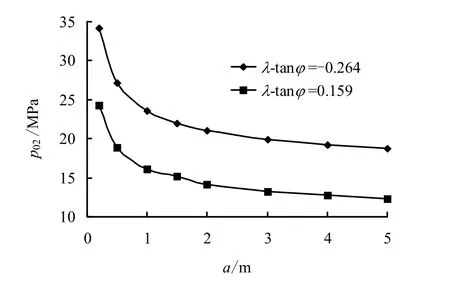
图5 压剪型裂纹p02 与a 关系曲线(β =60°) Fig.5 Relationships between p02 and a of shear-compression crack (β =60°)

当β =30°时，随着裂纹长度的增长，02p 也逐渐减小。可见随着裂纹长度增加，维持压剪型裂纹稳定的内水压力区间也越小，对于维持隧洞稳定也越不利，因此，在工程实际中，为保证隧洞安全稳定运行，洞壁出现的长裂缝应该受到足够的重视。当 tanλ φ- 的值由-0.264 增加到0.159 时，02p 与a关系曲线规律仍保持不变，但临界内水压力值出现较大的减小。可见发生压剪型破坏时，当围岩内摩擦角减小后，裂纹稳定区对应的内水压力区间减小，对隧洞稳定不利。比较图4、5 可知，当β 从30°提升至60°时，02p 与a 关系曲线规律仍保持不变，但当 tanλ φ- 的值由-0.264 增加到0.159 后，β =60°对应的临界内水压力减小幅度要高于β =30°。可见对于压剪型裂纹而言，当裂纹走向与洞壁法线方向夹角越大，由于围岩内摩擦角减小导致裂纹稳定区减小的幅度也越大。

3.3 裂纹埋深对临界水压力的影响

为研究裂纹埋深0r 对于临界水压力值的影响，分别对 0/r r 取1～2 范围内的值，β =0°时拉剪型裂纹02p 与 0/r r 关系曲线如图6 所示。可见随着裂纹埋深的增加，裂纹扩展所需的临界内水压力02p 越高。考虑到此时01p 均为负值，说明裂纹离洞壁越远，裂纹稳定区对应的内水压力区间越大，裂纹发生拉剪型扩展的难度越大。02p 值从 0/r r =1（表面裂纹）时的26.06 MPa 提高至 0/r r =2（深埋裂纹）时的74.24 MPa，增幅达到185%。可见深埋裂纹由于临界内水压力过高，其扩展的可能性要远小于表面裂纹，事实上，工程中对隧洞稳定最具威胁的是拉剪型裂纹，它一旦位于隧洞表面，则往往会对隧洞安全稳定运行构成威胁，因此，该情况在工程中应得到足够的关注。

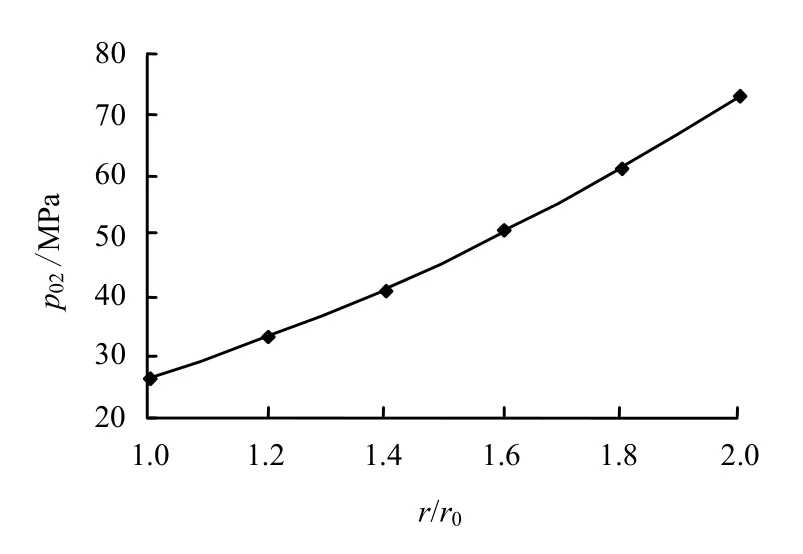
图6 拉剪型裂纹p02 与r/r0 关系曲线(β =0) Fig.6 Relationships between p02 and r/r0 of shear-tensile crack (β =0)

当β =30°、60°时，压剪型裂纹02p 与 0/r r 关系曲线分别如图7、8 所示。当β =30°时，随着裂纹 埋深的增加，02p 也逐渐增加，与拉剪型裂纹规律类似。当 tanλ φ- 的值由-0.264 增加到0.159 时，02p与 0/r r 关系曲线规律仍保持不变，但临界内水压力值出现较大的减小。可见发生压剪型破坏时，当围岩内摩擦角减小后，裂纹埋藏越深，裂纹稳定区对应的内水压力区间减小幅度越大。

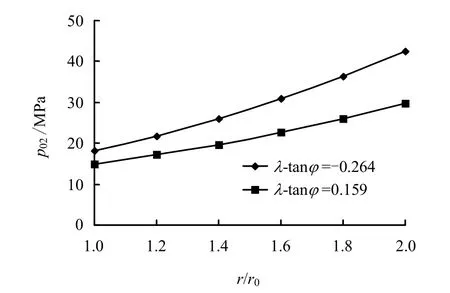
图7 压剪型裂纹p02 与r/r0 关系曲线(β =30°) Fig.7 Relationships between p02 and r/r0 of shear-compression crack(β =30°)

图8 压剪型裂纹p02 与r/r0 关系曲线(β =60°) Fig.8 Relationships between p02 and r/r0 of shear-compression crack (β =60°)

3.4 围岩孔隙水作用面积对临界水压力的影响

为研究围岩孔隙水作用面积对临界水压力值的影响，分别对η 取0～0.3 范围内的值。β =0°，a= 2.0 m 时拉剪型裂纹02p 与η 及 0/r r 关系曲线如图9所示。在该参数情况下随着围岩孔隙水作用面积系数的增长，02p 会有一定程度的降低。裂纹埋深越大，临界水压力值越大，裂纹发生拉剪型扩展的可能性就越小。

β =30°，c =1 MPa，a=2.0 m，λ - tanφ=-0.264时压剪型裂纹 p02与η 及 r /r0关系曲线如图10 所示。在该参数情况下随着围岩孔隙水作用面积系数的增长， p02会有一定程度的降低，与拉剪型裂纹p02与η 及 r /r0关系曲线规律类似。

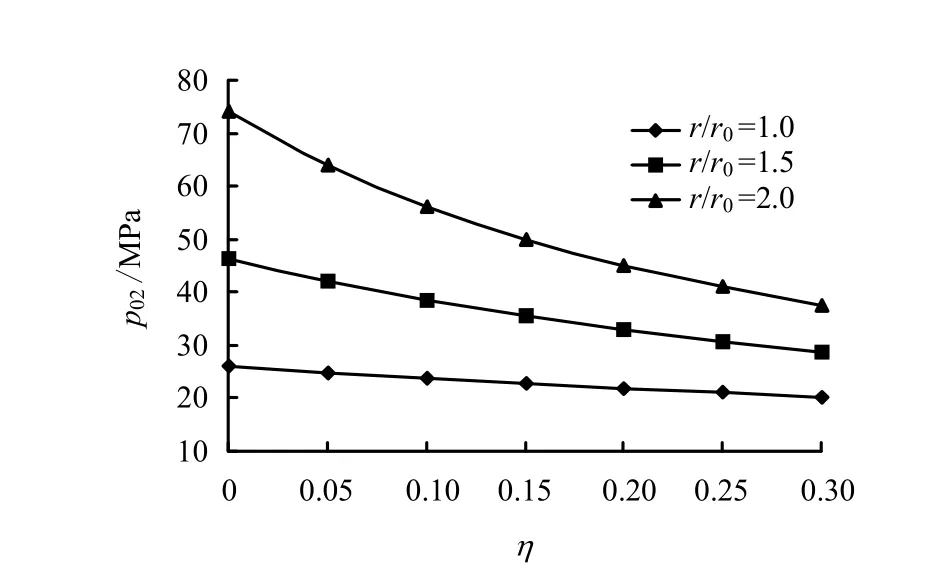
图9 拉剪型裂纹p02 与η及r/r0 关系曲线 Fig.9 Relationships between p02 and η of shear-tensile crack

图10 压剪型裂纹p02 与η及r/r0 关系曲线 Fig.10 Relationships between p02 and η of shear-compression crack

4 结 论

（1）在高内水压力的作用下，或者由于地应力释放的影响，裂纹既可能发生拉剪型扩展，也可能发生压剪型扩展，但后者发生的几率更大。这是由于拉剪型裂纹只有在裂纹长轴与最大主应力夹角为特定角度时才会发生，而且其对应的临界内水压力要高于前者。

（2）当裂纹走向垂直于洞壁法线方向时最为稳定，扩展的可能性比其他夹角情况下要小得多。

（3）随着裂纹长度增加，维持压剪型裂纹稳定的内水压力区间也逐渐减小，因此，在工程实际中，为保证隧洞安全稳定运行，洞壁出现的长裂缝应该受到足够的重视。

（4）深埋裂纹由于临界内水压力较高，其扩展的可能性要远小于表面裂纹，事实上，工程中对隧洞稳定最具威胁的是拉剪型裂纹，拉剪型裂纹一旦位于隧洞表面，则往往会对隧洞安全稳定运行构成威胁。

（5）在内水压力控制下，围岩孔隙水作用面积越大，裂纹越容易发生扩展。

[1] 赵阳升. 矿山岩石流体力学[M]. 北京: 煤炭工业出版社, 1995.

[2] HUBBERT M K, WILLIS D G. Mechanics of hydraulic fracturing transactions[J]. American Institute of Mining Engineers, 1957, 210: 153－168.

[3] 黄润秋, 王贤能, 陈龙生. 深埋隧道涌水过程的水力劈裂作用分析[J]. 岩石力学与工程学报, 2000, 19(5): 573－576. HUANG Run-qiu, WANG Xian-neng, CHEN Long-sheng. Hydraulic fracturing analysis in water-spouting process in deep-lying tunnels[J]. Chinese Journal of Rock Mechanics and Engineering, 2000, 19(5): 573－576.

[4] 盛金昌, 赵坚, 速宝玉. 高水头作用下水工压力隧洞的水力劈裂分析[J]. 岩石力学与工程学报, 2005, 24(7): 1226－1230. SHENG Jin-chang, ZHAO Jian, SU Bao-yu. Analysis of hydraulic fracturing in hydraulic tunnels under high water pressure[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(7): 1226－1230.

[5] 李宗利, 张宏朝, 任青文, 等. 岩石裂纹水力劈裂分析与临界水压计算[J]. 岩土力学, 2005, 26(8): 1216－1220. LI Zong-li, ZHANG Hong-chao, REN Qing-wen, et al. Analysis of hydraulic fracturing and calculation of critical internal water pressure of rock fracture[J]. Rock and Soil Mechanics, 2005, 26(8): 1216－1220.

[6] 黄达, 金华辉, 黄润秋. 拉剪应力状态下岩体裂隙扩展的断裂力学机制及物理模型试验[J]. 岩土力学, 2011, 32(4): 997－1002. HUANG Da，JIN Hua-hui，HUANG Run-qiu. Mechanism of fracture mechanics and physical model test of rocks crack expanding under tension-shear stress[J]. Rock and Soil Mechanics, 2011, 32(4): 997－1002.

[7] 邓华锋, 李建林, 刘杰, 等. 考虑裂隙水压力的岩体压剪裂纹扩展规律研究[J]. 岩土力学, 2011, 32(增刊1): 297－302. DENG Hua-feng, LI Jian-lin, LIU Jie, et al. Research on propagation of compression shear fracture in rocks considering fissure water pressure[J]. Rock and Soil Mechanics, 2011, 32(Supp. 1): 297－302.

[8] 刘涛影, 曹平, 章立峰, 等. 高渗压条件下压剪岩石裂纹断裂损伤演化机制研究[J]. 岩土力学, 2012, 33(6): 1801－1808. LIU Tao-ying, CAO Ping, ZHANG Li-feng, et al. Study of fracture damage evolution mechanism of compression-shear rock cracks under high seepage pressure[J]. Rock and Soil Mechanics, 2012, 33(6): 1801－1808.

[9] 蔡晓鸿, 蔡勇平. 水工压力隧洞结构应力计算[M]. 北京: 中国水利水电出版社, 2004.

[10] 徐芝纶. 弹性力学简明教程[M]. 北京: 高等教育出版社, 2002.

[11] 龚晓南. 土力学[M]. 北京: 中国建筑工业出版社, 2002.

[12] ERDOGAN F, SIH G C. On the crack extension in plates under plane loading and transverse shear[J]. Journal of Basic Engineering, 1963, 85: 519－527.

[13] 周群力, 刘格非. 脆性材料的压剪断裂[J]. 水利学报, 1982, (7): 63－69. ZHOU Qun-li, LIU Ge-fei. Compressive shear fracture of brittle material[J]. Journal of Hydraulic Engineering, 1982, (7): 63－69.