富含黏土矿物的低渗砂岩变形响应特征研究
肖文联,赵金洲,李 闽,王 俊,李丽君
(西南石油大学 油气藏地质及开发工程国家重点实验室,成都 610500)
1 引 言
渗透率k 与围压Pc和孔隙流体压力(孔压)Pp的函数关系可表示为k =f (Peff) =f (Pc-nkPp),其中Peff为有效应力,nk为渗透率有效应力系数ESCK,用来表征孔压相对围压作用对渗透率的影响程 度[1-3]。国内外对于ESCK 的研究主要针对孔隙型岩石和裂缝型岩石两大类开展。
对于孔隙型岩石:Zoback 等[4]试验发现,Barre 孔隙型砂岩的nk为4.0 和2.2,并提出黏土壳状概念模型解释了试验结果。Nur 等[5]试验发现含黏土的孔隙型砂岩nk为大于1.0 的常数,变化范围为1.2~7.1,并随黏土含量的增加而增加;不含黏土的2 块Al2O3人造岩芯的nk分别是0.43 和0.86。Berryman[6]提出了“双组分模型”(将岩石骨架中易于压缩的黏土矿物单独视为一个组分)代替“等效模型”,并结合渗透率与电导率的相似性推导出含黏土孔隙型岩石的ESCK,发现ESCK 与黏土含量、骨架和黏土的弹性模量、孔隙度等参数有关,而这些参数均为常数,则认为nk为常数;当岩石中含有黏土矿物时,nk>1.0,如果黏土矿物与岩石骨架之间的弹性模量差异越大(黏土矿物越容易压缩),那么nk就越大,甚至远大于1.0;同时,把2 个组分视为1 个组分时得到了单组分岩石ESCK 的表达式,结果发现,nk是在变化范围孔隙度φ ~1.0 之间的常数;这与以往试验结果一致。Wl-Wardy 等[3]对1 块富含黏土孔隙型砂岩进行试验发现nk=5.4,提出了黏土粒状模型,结合Zoback 等[4]提出的黏土壳状模型获得ESCK 解析解,并发现ESCK 随黏土矿物含量的增加而增加。Zhao 等[7]对4 块富含黏土孔隙型砂岩的试验研究发现,ESCK 为大于1.0 的常数,甚至高达6.16,与黏土矿物的类型有关。综上所述,孔隙岩石的ESCK为常数;不含黏土矿物岩石,ESCK 值小于1.0;含黏土矿物岩石,ESCK 大于1.0;黏土矿物的含量和类型直接影响ESCK。
对于(微)裂缝型岩石:Walsh[8]根据渗透率与热传导的相似性,推导出单组分岩石二维平面裂缝模型的ESCK,发现nk<1.0,且为应力的函数;此外,还指出ESCK 与岩石的流通通道形状有关,并给出了当流通通道截面积为圆形时,ESCK 的变化范围为0.4~1.0。随后,Bernabe[1]把裂缝截面视为长半轴为a、短半轴为b 的椭圆,建立了单组分裂缝型岩石二维平面椭圆裂缝模型,推导出裂缝型岩石ESCK 的表达式,认为ESCK 与a/b、泊松比ν有关;当为无限长裂缝(a ≫b)时,nk=1.0,随有效应力的增加(围压增加或者孔压降低),裂缝将逐渐闭合,ESCK 也随之减小,最终裂缝将具有圆形孔隙特征(a =b),nk达到下限值(1+ν)/2;同时,他还对裂缝花岗岩进行了试验研究,发现nk随应力变化而变化,其变化范围为0.4~1.0,与单组分椭圆裂缝模型ESCK 的变化规律一致。Warpinski 等[9]观察到微裂缝砂岩(含极少量黏土)的nk为0.55~1.10,低压下nk=1.0。郑玲丽等[10]采用修正的响应面方法分析3 块裂缝花岗岩的数据发现,nk在0.42~0.83 之间,并符合有效应力的概念。李闽 等[11-13]发现,微裂缝砂岩(含极少量黏土)的nk为0~1.24,并随着应力的变化而变化;笔者基于Berryman 和Bernabe 的观点提出了裂缝概念模型,指出对于完全张开的单组分裂缝(a ≫b,nk=1.0),裂缝将逐渐闭合,a 与b 的比值减小,ESCK 减小,岩石体现出裂缝的显著变形特征;随有效应力的进一步增加,岩石中也随之出现a ≈b 相近的圆形管束(圆形管束的变形稳定),ESCK 将进一步减小,此时岩石以裂缝变形为主,同时伴随骨架的变形;有效应力地继续增加将使岩石中的椭圆全都变成或者近似变为圆形管束,岩石性质稳定,ESCK 将达到下限值φ,此时岩石表现为孔隙型介质的变形特征——骨架颗粒的显著变形。Ghabezloo 等[14]针对含黏土微裂缝石灰岩进行了试验和理论研究,发现ESCK 值为0.9~2.4,与黏土矿物壳状模型相符合。因此,(微)裂缝的存在使得ESCK 随应力的变化而变化,并且黏土矿物的存在也影响ESCK。对于单组分裂缝岩石,ESCK 值在φ ~1 之间变化;对于含黏土裂缝,ESCK 是大于1.0 的变化值。
以往研究表明,黏土矿物的类型和含量以及岩石孔隙类型等影响ESCK 的变化规律。为进一步认识黏土矿物等对ESCK 的影响,尤其是对岩石变形特征的影响,本文将从ESCK 的含义入手,分析前人研究的成果,探讨ESCK 与岩石变形特征之间的关系,初步形成一套诊断岩石变形特征的方法;开展ESCK 的试验,提出平移法分析处理试验数据,获取ESCK 值;根据形成的诊断方法判断以往和本文研究的31 块岩石变形特征,并结合微观特征研究对比分析诊断结果。
2 诊断方法
随着岩石应力状态的变化(改变围压或孔压),岩石本身也将发生变形并引起孔隙结构改变,然而改变围压或孔压对岩石变形和孔隙结构改变的影响程度是不同的,表现出对岩石渗透率变化的影响程度也不相同,根据ESCK 的定义即对应的ESCK 值也不相同。因此,ESCK 可响应岩石的孔隙结构变化,反映不同岩石在不同应力状态下的变形响应特征,称为岩石变形响应特征参数。
前人对ESCK 与岩石变形响应特征研究成果可归结为如下特征:(1)单组分岩石ESCK 小于1.0,双组分岩石(含黏土)ESCK 大于1.0;(2)孔隙性岩石ESCK 为常数,裂缝性岩石ESCK 为变量。于是,不含黏土孔隙性岩石,ESCK 为小于1.0 的常数,当应力变化时岩石骨架变形显著(见图1(a));含黏土孔隙性岩石,ESCK 为大于1.0 的常数,当应力变化时骨架和黏土均变形显著(见图1(c));不含黏土裂缝性岩石,ESCK 小于1.0 且随应力的变化而变化,表现为岩石裂缝变形显著(见图1(b));含黏土裂缝性岩石,ESCK 大于1.0 且随应力的变化而变化,表现为黏土和裂缝变形显著(见图1(d))。ESCK的大小和变化特征响应了岩石的变形特征,这为诊断岩石变形特征提供了新的依据。
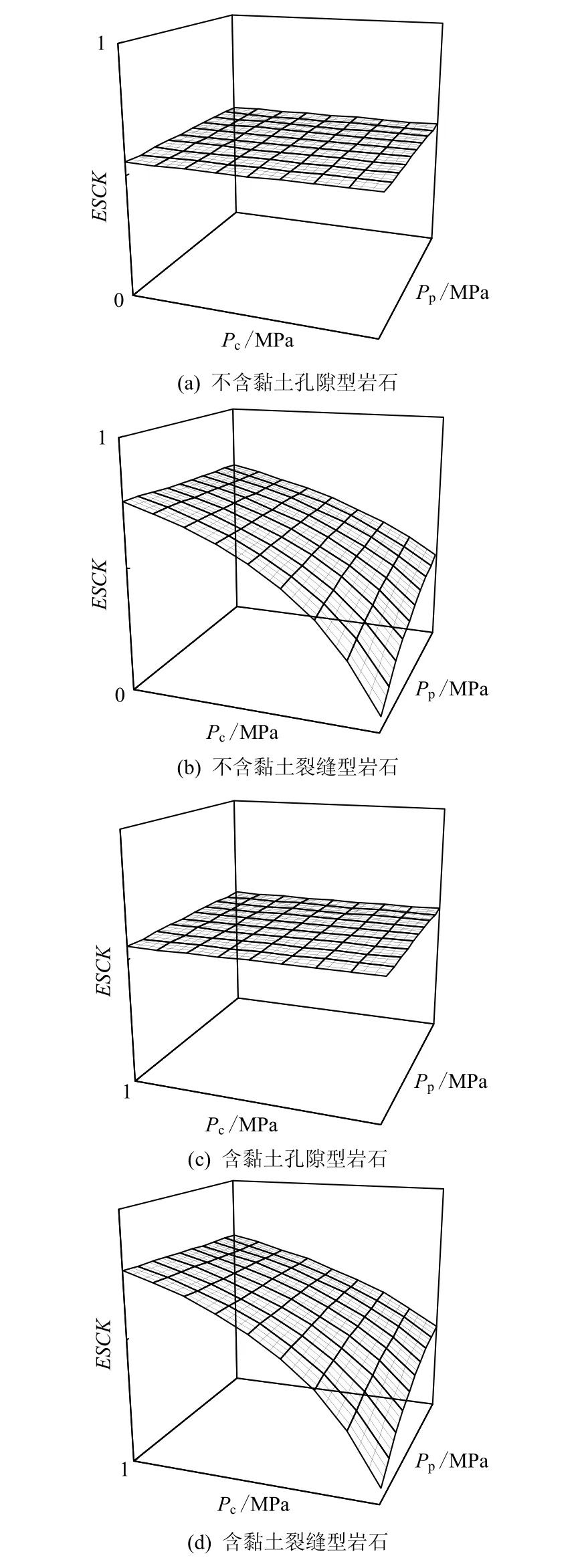
图1 ESCK 与岩石的变形响应特征 Fig.1 Relationships between ESCK and response characteristics of rock deformation
3 ESCK 试验研究
3.1 试验岩样
本试验选取2 块低渗透性砂岩,其渗透率和孔隙度分别为:P1(k=0.383 mD、φ=11.47%)、P2(k=0.299 mD、φ=11.23%)。由X 衍射结果可知,2 块岩芯黏土矿物含量分别为14.9%和18.7%;黏土矿物以伊利石/蒙脱石混层(分别为35%和45%)和绿泥石/蒙脱石混层(分别为31%和40%)为主,还含有一定量的高岭石和蒙脱石(约为20%)。图2(a)中的进汞曲线表明,孔喉分选性好,图2(b)的渗透率贡献值与孔喉分布曲线表明,门槛压力附近对应的孔喉对渗透率贡献最大;电镜扫描图(见图3)可观察到岩石颗粒大小比较均匀,岩石无裂隙。因此,所选岩样为富含黏土的孔隙型砂岩。
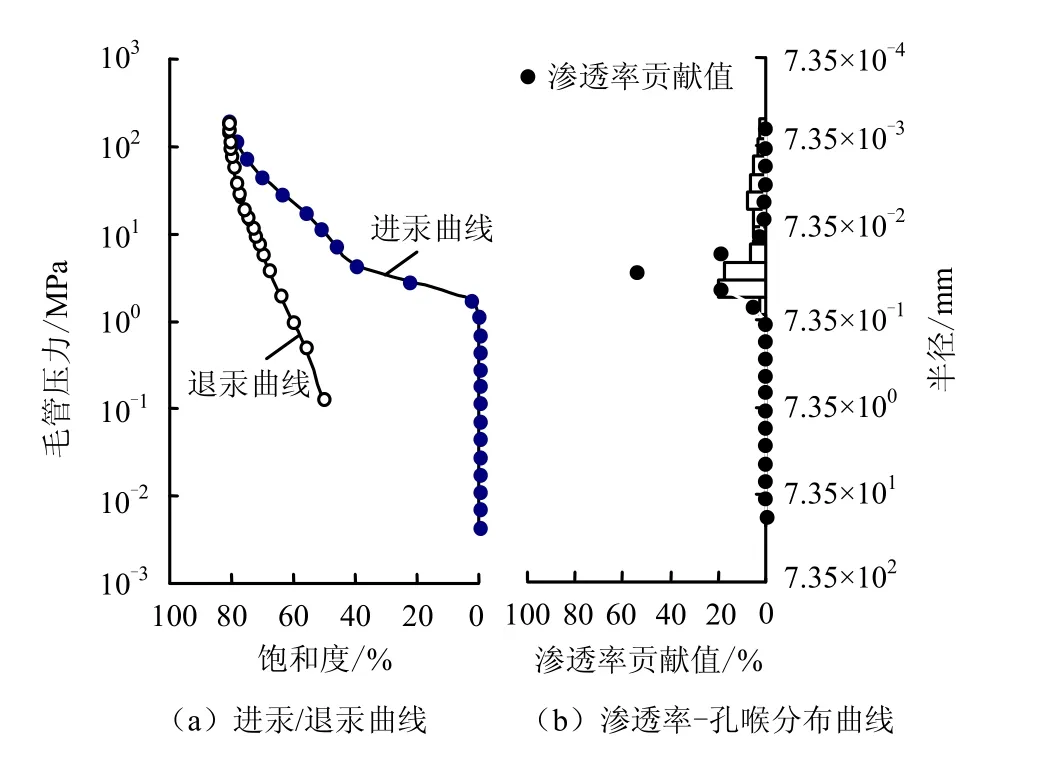
图2 P2 毛细管压力曲线 Fig.2 Capillary pressure curve of sample P2

图3 P2 电镜扫描图 Fig.3 Scanning electron microscopy of sample P2
3.2 试验流程
采用稳态法装置[11-13,15]测试岩石的渗透率,试验流体为氮气。渗透率测试试验在3 个不同围压下分步加/卸载孔隙流体压力,围压和孔隙流体压力依据试验岩芯所处的地层条件而设计(见图4、5)。每个测试点重复测试5 次并取平均值计算渗透率。在试验之前,需要对试验岩芯进行老化处理[11-13,15]以使得岩石性质变得更加稳定。
3.3 试验数据
试验结果(见图4、5)包含不同围压下加/卸载孔隙流体压力循环的试验数据,a 表示加载过程,b 表示卸载。试验结果表明,渗透率随围压的增加而减小,随孔隙流体压力的增加而增加。
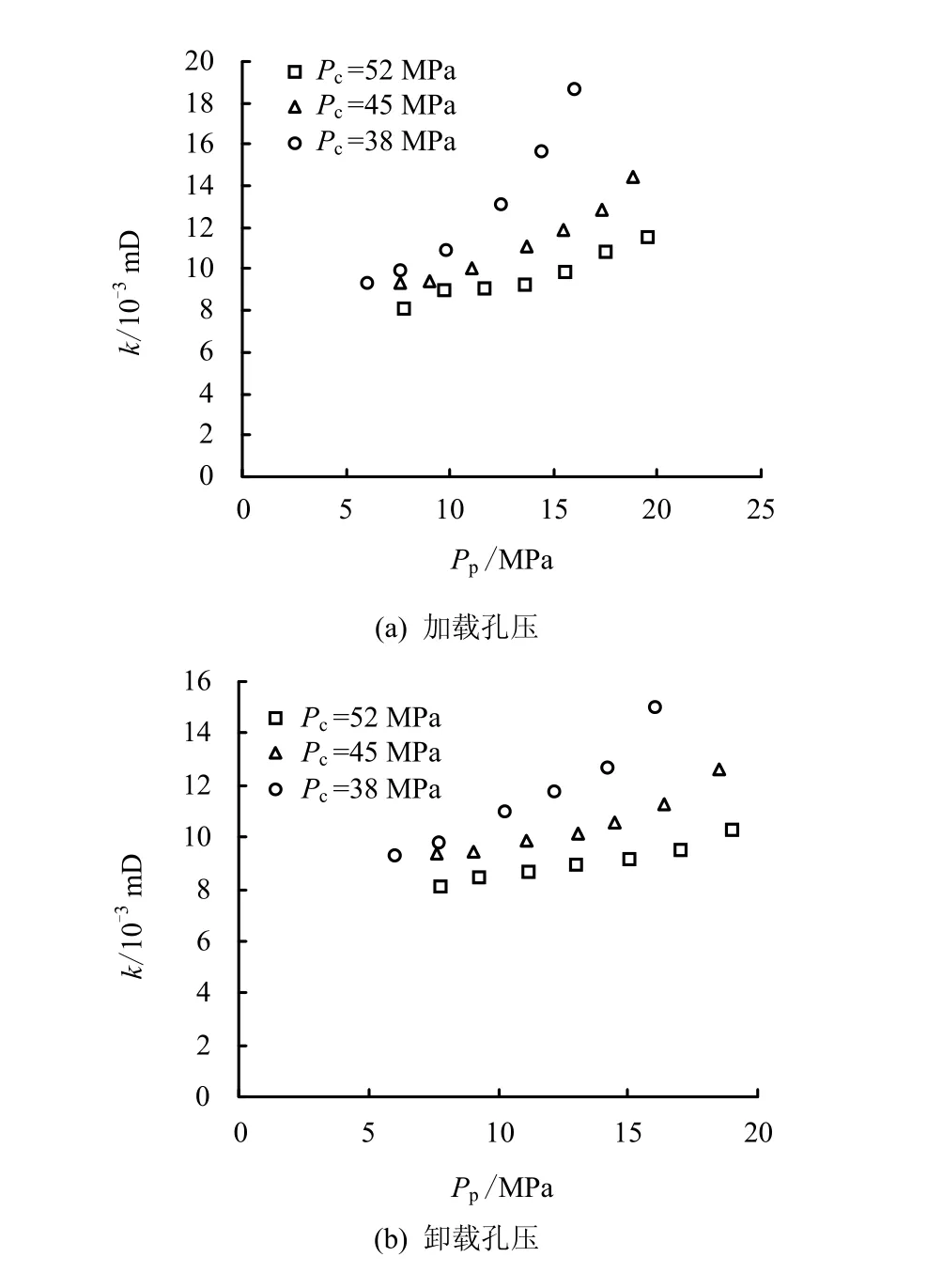
图4 P1 砂岩k-Pc-Pp 之间的关系 Fig.4 Relationships of k-Pc-Pp of Sample P1
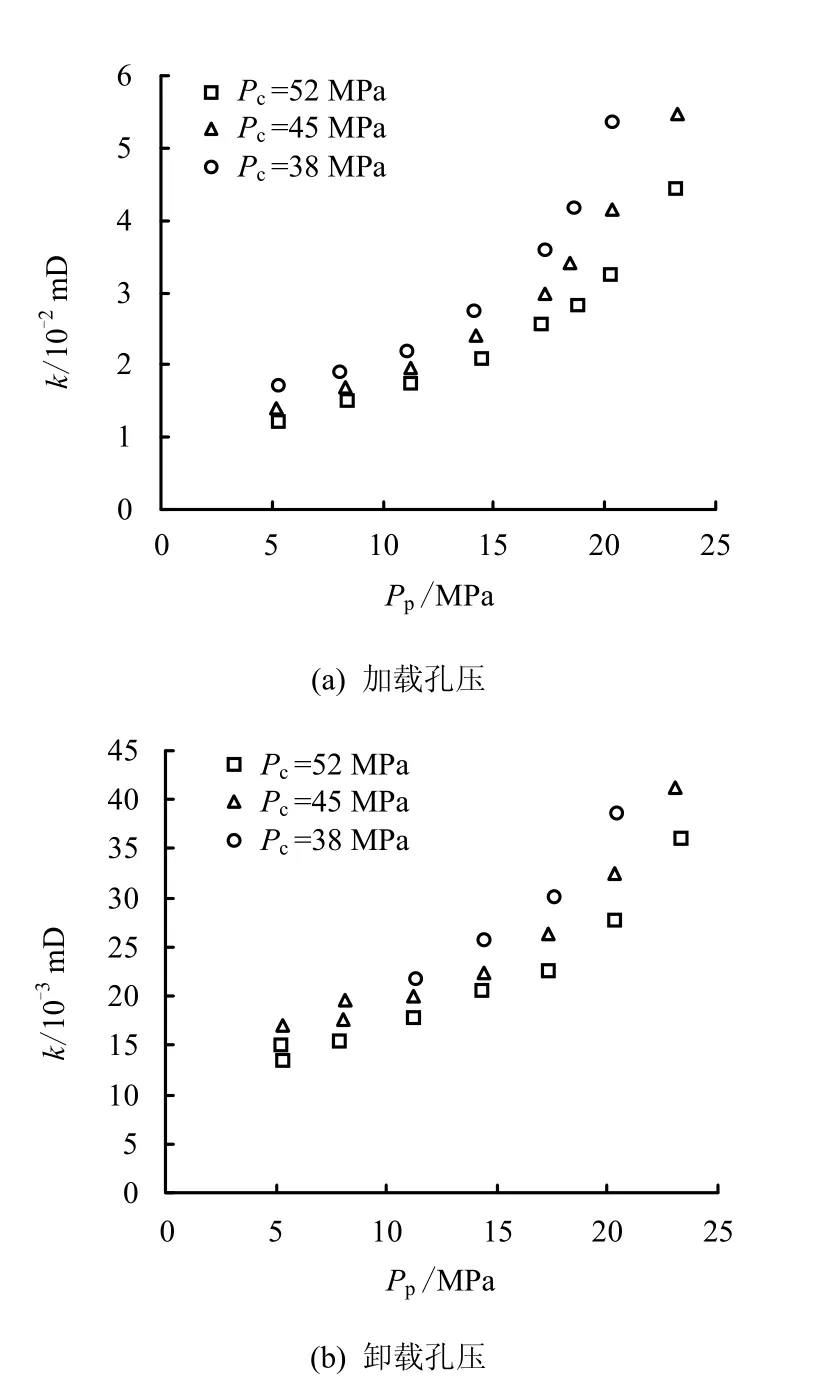
图5 P2 砂岩k-Pc-Pp 之间的关系 Fig.5 Relationships of k-Pc-Pp of Sample P2
3.4 ESCK 计算
ESCK 的计算表达式为[1-2]
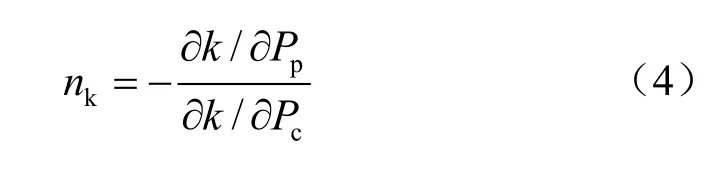
分别单独改变围压 cPδ 和孔隙流体压力 pPδ 可使得渗透率的改变量 kδ 相同,进而使得2 个偏微分化简,于是式(4)可以写为

对于定围压下改变孔隙流体压力的曲线(见图4、5),ESCK 的确定步骤如下:选择不同围压下渗透率与孔隙流体压力的曲线中的任何一条作为参考曲线,其余每条曲线沿Pp轴平移并与参考曲线重合(每条曲线中的每个点改变相同的孔隙流体压力值pPδ ),记录平移过程中曲线之间围压和孔隙流体压力的改变量 cPδ 和 pPδ ,然后代入式(5)计算nk,同时采用三项式(k/kref=a1(Peff/Pref)2+a2Peff/Pref+ a3)、指数(k/kref=b1exp(b2Peff/Pref))和乘幂(k/kref= (Peff/Pref)c1)关系拟合渗透率k 与有效应力(Peff= Pc-nkPp)的关系(其中a1、a2、a3、b1、b2和c1为拟合系数,kref为参考有效应力Pref下的渗透率),依据拟合相关系数R2和残差均方根判断平移效果是否达到最佳以及确定渗透率与有效应力满足的关系——当R2最大和SR最小时平移效果最佳,对应渗透率与有效应力的拟合效果最佳,于是称该方法为平移法。本文是将高围压和低围压下的2 条渗透率与孔隙流体压力曲线同时向中间围压的曲线平移相同的 pPδ ,使3 条曲线重合,同时这也满足高围压和低围压向中间曲线平移时围压的变化量相等(见图6),结果见表1。
选择拟合效果最好关系式对应的ESCK 值为所求的值。根据表1 的计算结果,P1 和P2 岩芯的渗透率与有效应力的关系分别满足乘幂关系和三项式关系,因此,P1 和P2 的ESCK 分别为(加载:1.136 4,卸载:1.020 4)和(加载:2.272 7,卸载:2.381 0),这说明研究岩芯的ESCK 是大于1.0 的常数,不随应力的变化而变化。
获取ESCK 之后,有必要评价计算方法的有效性和计算结果的可靠性。具体步骤:(1)计算有效应力Peff(Peff=Pc-nkPp);(2)建立渗透率与有效应力的关系;(3)与经典的Terzaghi 有效应力与渗透率的关系进行对比,评价本文获取的渗透率与有效应力的关系,评价依据是相同有效应力对应的渗透率值相等。基于平移法(Peff-P=Pc-nkPp)建立的渗透率与有效应力的关系与基于Terzaghi 有效应力(Peff-T=Pc-Pp)建立的渗透率与有效应力的关系(见图7),结合表1 中所示的平移法得到的渗透率与有效应力之间的相关拟合系数都接近1.0,这表明基于平移法得到渗透率与有效应力之间的对应关系更好,具有相等有效应力渗透率相等的一一对应关系,计算结果符合有效应力的概念,因此,证明本文提出的计算方法是可行的,也说明经典的Terzaghi 有效应力不适于本文研究的岩石。

表1 ESCK、拟合相关系数R2 和残差均方根SR Table 1 ESCK、Fitting correlation coefficient R2 and root mean square residual SR
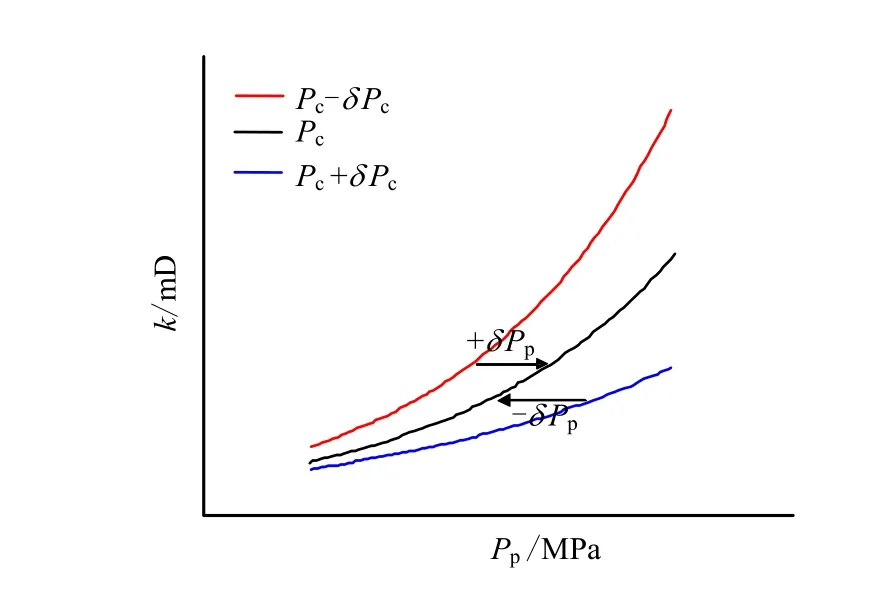
图6 平移法示意图 Fig.6 Schematic diagram of the translation method
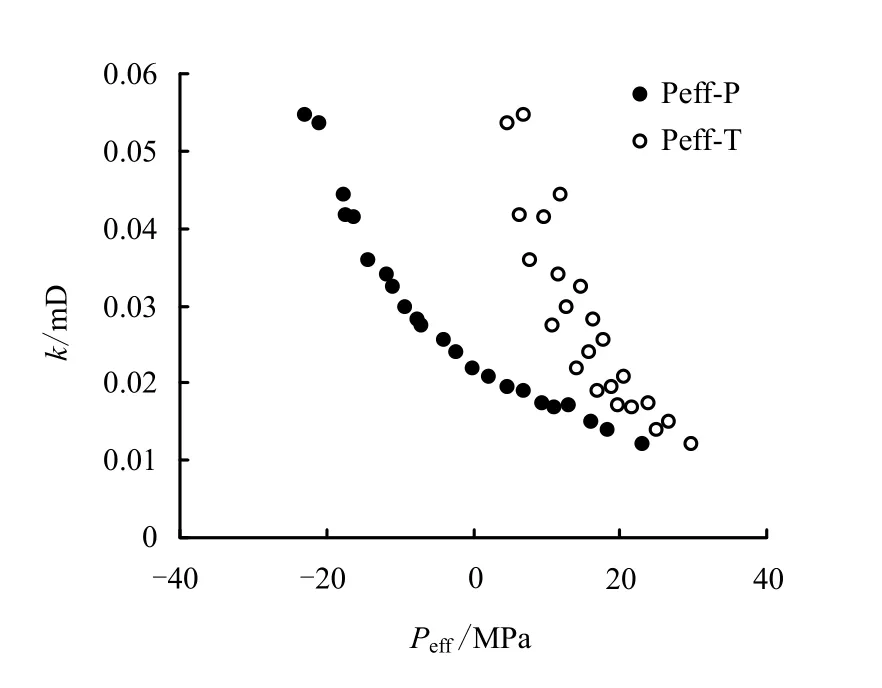
图7 渗透率与有效应力的关系图 (P2(a)) Fig.7 Relationships between permeability and effective pressure of Sample P2 (a)
4 岩石变形特征诊断
岩芯P1 和P2 的ESCK 分别为1.136 4 和2.272 7,其特征与图1(c)一致,这说明两块岩芯的变形表现为黏土的变形显著,并可伴随岩石骨架颗粒的变形,这与岩石微观特征为富含黏土孔隙型砂岩一致。同时,分析发现Nur 等[5]的7 块Berea 砂岩、Wl-Wardy 等[3]的1 块Stainton 砂岩、Zoback 等[4]的2 块Berea 砂岩以及Zhao 等[7]的4 块砂岩——总计14 块富含黏土孔隙型砂岩的ESCK 都是大于1.0 的 常数,与本文研究的岩石具有相同的变形特征。结合ESCK 的大小与黏土矿物的含量发现,黏土含量越多,ESCK 越大,表明岩石变形时黏土的变形越显著。然而,对比岩芯中的黏土矿物进一步分析发现,Zhao 等[7]的研究中有2 块岩石中伊利石和绿泥石含量相对较多,黏土含量高达22.5%,然而ESCK相对最小(为1.1);而Zhao 等[7]剩下的2 块岩芯和本文研究岩芯主要以伊利石/蒙脱石混层和绿泥石/蒙脱石混层为主,并包含高岭石和蒙脱石,剩余其他岩芯中的黏土矿物都是高岭石,ESCK 相对较大,甚至高达7.1。这说明相对前者,后者所对应的岩石变形相应特征更加显著。其原因可能是前者对应岩芯中伊利石和绿泥石的含量相对较多,而后者对应岩石中高岭石、蒙脱石、伊利石/蒙脱石混层和绿泥石/蒙脱石混层相对较多;伊利石和绿泥石晶间距离更小,性质也更加稳定,从而表现出相对较小的压缩性[17-19]。因此,黏土矿物类型影响岩石的变形特征。
Nur 等[5]还研究了2 块Al2O3造的孔隙型岩芯,发现ESCK 分别为0.43 和0.86,这与图1(a)所示特征一致,说明这两块人造岩芯骨架颗粒的变形特征显著,与岩芯是不含黏土矿物的孔隙型结构特征相符。
再者,Bernabe[1]的3 块裂缝Chelmsford 花岗岩(0.4<nk<1.0)、Warpinski 等[9]的2 块微裂缝砂岩(0.55<nk<1.1)、郑玲丽等[10]的 3 块花岗岩(0.42≤nk≤0.83)和李闽等[11-12]的7 块微裂缝砂岩(0≤nk≤1.23)的ESCK 都不是常数,随应力的变化而变化,变化范围主要在0~1.0 之间,例如李闽等[11]研究的S1 岩芯ESCK 变化特征(见图8(a))与岩石的微观特征——存在微裂缝(见图8(b)),ESCK 与图1(b)相对应的特征,说明岩石裂缝变形显著,这与岩石具有裂缝的微观特征一致。
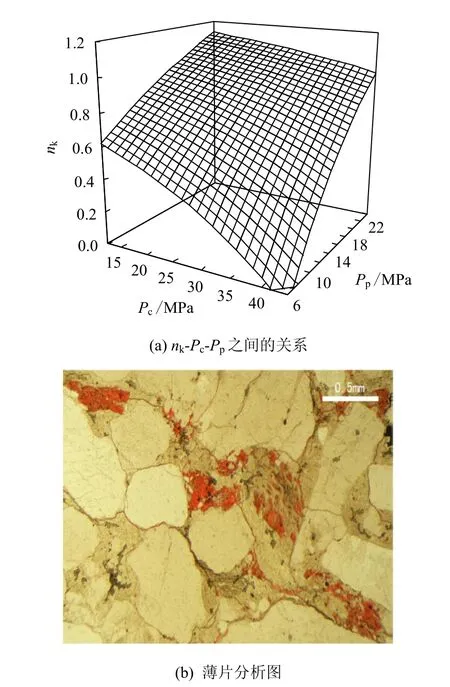
图8 李闽等[12]研究中S1 岩芯的ESCK 与其微观特征 Fig.8 ESCK and microstructure of S1[12]
因此,ESCK 响应了岩石的变形特征,并且与岩石的微观特征一致。黏土矿物的类型和含量以及岩石的孔隙类型是影响岩石变形的主要因素。本文研究岩芯和以往研究岩芯的变形特征诊断结果见表2。
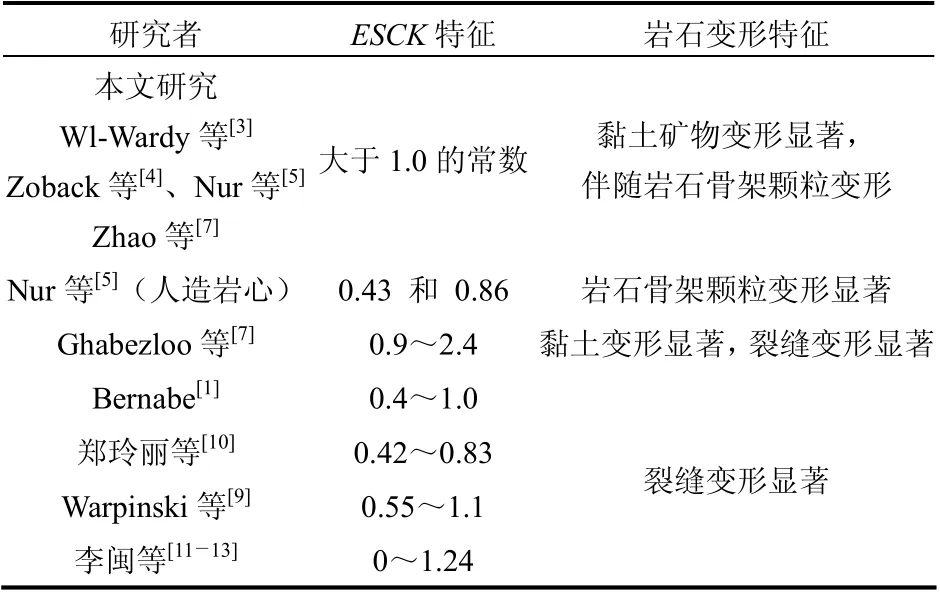
表2 ESCK 与岩石变形响应特征 Table 2 ESCK and deformation response characteristics of rock
5 结 论
(1)开展了2 块岩芯的渗透率随应力变化规律的试验,提出了平移法并分析试验数据;结果表明试验岩芯的ESCK 值为大于1.0 的常数;基于平移法得到的渗透率与有效应力之间的拟合相关系数接近1.0,并且好于渗透率与Terzaghi 有效应力之间的关系;这说明本文提出的平移法是一种可靠的计算方法,Terzaghi 有效应力不适于本文研究的岩石。
(2)研究发现,ESCK 是岩石的变形响应特征参数,据此建立了渗透率有效应力系数与岩石变形响应特征之间的关系,提出了诊断岩石变形特征的新方法。
(3)诊断发现,本文研究的富含黏土孔隙型砂岩以黏土矿物的变形为显著特征,同时还结合微观特征诊断了以往研究的岩芯,发现岩石的变形特征与其微观结构特征一致,黏土矿物的类型影响岩石的变形特征。
[1] BERNABE Y. The effective pressure law for permeability in Chelmsford granite and Barre granite[J]. International Journal of Rock Mechanics and Mining Sciences, 1986, 23(3): 267-275.
[2] BERNABE Y. The effective pressure law for permeability during pore pressure and confining pressure cycling of several crystalline rocks[J]. Journal of Geophysical Research, 1987, 92(B1): 649-657.
[3] AL-WARDY W, ZIMMERMAN R W. Effective stress law for the permeability of clay-rich sandstones[J]. Journal of Geophysical Research, 2004, 109: B04203.doi: 10.1029/2003JB002836.
[4] ZOBACK M D, BYERLEE J D. Permeability and effective stress[J]. AAPG Bulletin, 1975, 59(1): 154-158.
[5] NUR A, WALLS J D, WINKLER, et al. Effects of fluid saturation on waves in porous rock and relations to hydraulic permeability[J]. SPE Journal, 1980, 26(2): 450-458.
[6] BERRYMAN J G. Effective stress for transport properties of inhomogeneous porous rock[J]. Journal of Geophysical Research, 1992, 97(B12): 17409-17424.
[7] ZHAO J Z, XIAO W L, LI M, et al. The effective pressure law for permeability of clay-rich sandstones[J]. Petroleum Science, 2011, 8(2): 194-199.
[8] WALSH J B. Effect of pore pressure and confining pressure on fracture permeability[J]. International Journal of Rock Mechanics and Mining Sciences, 1981, 18(5): 429-435.
[9] WARPINSKI N R, TEUFEL L W. Determination of the effective stress law for permeability and deformation in low-permeability rocks[J]. SPE Journal, 1992, 7(2): 123-131.
[10] 郑玲丽, 李闽, 肖文联, 等. 最大似然函数法确定渗透率有效应力系数[J]. 新疆石油地质, 2008, 29(6): 747-
749. ZHENG Ling-li, LI Min, XIAO Wen-lian, et al. Determination of effective stress coefficient of permeability using maximum- likelihood function approach[J]. Xinjiang Petroleum Geology, 2008, 29(6): 747-749.
[11] 李闽, 肖文联. 低渗砂岩储层渗透率有效应力定律试验研究[J]. 岩石力学与工程学报, 2008, 27(增刊2): 3535-3540. LI Min, XIAO Wen-lian. Experimental study of permeability-effective-stress law in low-permeability sandstone reservoir[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(Supp.2): 3535-3540.
[12] 李闽, 肖文联, 郭肖, 等. 塔巴庙低渗致密砂岩渗透率有效应力定律实验研究[J]. 地球物理学报, 2009, 52(12): 3116-3174. LI Min, XIAO Wen-lian, GUO Xiao, et al. Laboratory study of the effective pressure law for permeability in Ta-Ba-Miao low-permeability sandstones[J]. Chinese Journal of Geophysics, 2009, 51(12): 3166-3174.
[13] LI M, BERNABÉ Y, XIAO W L, et al. Effective pressure law for permeability of E-bei sandstones[J]. Journal of Geophysical Research, 2009, 114: B07205. doi: 10.1029/2009JB006373.
[14] GHABEZLOO S, SULEM J, SYLVINE G, et al. Effective stress law for the permeability of a limestone[J]. International Journal of Rock Mechanics and Mining Sciences, 2009, 46(2): 297-306.
[15] 肖文联, 李闽, 赵金洲, 等. 低渗致密砂岩渗透率应力敏感性试验研究[J]. 岩土力学, 2010, 31(3): 775-779. XIAO Wen-lian, LI Min, ZHAO Jin-zhou, et al. Laboratory study of stress sensitivity to permeability in tight sandstone[J]. Rock and Soil Mechanics, 2010, 31(3): 775-779.
[16] WILLIAMS E J. Regression analysis[M]: New York: John Wiley & Sons Inc., 1959.
[17] 任磊夫. 试论黏土矿物转化过渡结构[J]. 沉积学报, 1988, 6(1): 80-87. REN Lei-fu. Intermediate structures of clay minerals during transformation[J]. Acta Sedimentologica Sinica, 1988, 6(1): 80-87.
[18] 杨献忠, 叶念军. 蒙脱石伊利石转化过程中伊-蒙混层形成的Gibbs 自由能[J]. 地质地球化学, 2003, 31(3): 20-25. YANG Xian-zhong, YE Nian-jun. Gibbs free energies of formation for mixed-layer illite-montmorillonite in the process of montmorillonite illitization[J]. Geology- Geochemistry, 2003, 31(3): 20-25.
[19] 赵杏媛, 张有瑜. 黏土矿物与黏土矿物分析[M]. 北京: 海洋出版社, 1990.

