抗滑桩加固边坡三维数值分析中的几个问题
年廷凯 ,徐海洋,刘红帅
(1. 大连理工大学 土木水利学院 海岸和近海工程国家重点实验室,辽宁 大连 116024;
2. 成都理工大学 地质灾害防治与地质环境保护国家重点实验室,成都 610059;3. 中国地震局工程力学研究所,哈尔滨 150080)
1 引 言
抗滑桩是一种大截面、侧向受荷的排桩或桩群,它穿过滑体锚入滑床一定深度,借助与桩周岩土的共同作用,将滑坡推力传递到稳定地层,其抗滑机制体现于桩、滑体与滑床3 者间的相互协调工作[1]。几十年来,许多学者针对抗滑桩开展了大量的研究,综合现有的文献成果,大体上可分为3 类:(1)理论分析,通过建立相应的数学或物理模型,研究土体侧向移动对抗滑桩的影响[2-9];(2)数值模拟,主要利用有限元或有限差分法,建立二维或三维数值计算模型,研究桩-土相互作用下桩身变形与内力分布,桩周土体应力和变形情况[10-16];(3)试验研究,通过室内小比尺物理模型与离心试验等[17-18],直观研究桩-土相互作用及抗滑桩工作性能。
在这3 类研究工作中,数值分析方法得到了快速发展和广泛关注,特别是基于强度折减技术的有限元或有限差分法[10-17],给抗滑桩加固边坡的数值模拟注入了新的活力。然而,通过综合分析文献资料,笔者注意到抗滑桩数值分析中仍有几个问题有待明晰,如抗滑桩计算模型尺度、桩底接触模式、加固位置、适宜桩长、桩间距与桩径比、桩头约束条件及临界滑动面等。为此,利用考虑桩-土-边坡相互作用的强度折减有限元方法[19],结合典型算例边坡,开展了抗滑桩加固边坡的三维数值分析,着重研究了抗滑桩-边坡体系的计算模型尺度、设桩位置、桩间距与桩径比、桩长与桩底接触模式等因素对边坡安全系数及临界滑动面的影响,以及不同桩头约束下抗滑桩内力分布等,以期为抗滑桩工程设计及规范修订提供参考。
2 强度折减有限元法
利用有限元程序进行强度折减计算,边坡土体采用服从Mohr-Coulomb 破坏准则与非关联流动法则的理想弹塑性本构模型。抗滑桩被视为理想线弹性体,桩-土间采用接触相互作用,摩擦系数取为0.3,约为tan(0.75φ)。以数值迭代不收敛并结合坡面特征点位移陡增作为边坡失稳判据[19],即在此时的强度折减系数为边坡稳定安全系数。强度折减计算中,折减后的强度参数表达式为

式中:c′和φ′为土体的实际抗剪强度参数;mc′ 和mφ′为土体发挥的抗剪强度参数;SRF 为强度折减系数。

图1 抗滑桩-边坡模型的侧面、平面图 Fig.1 Side view and plan view for slope-pile model

表1 抗滑桩-边坡土性质参数 Table 1 Properties of soil and pile
3 抗滑桩-边坡计算模型尺度问题
针对当前抗滑桩加固三维边坡数值计算中桩-边坡体系计算模型尺度选择的问题,这里建立单桩取半、单桩、双桩取半、双桩、单桩加双桩取半5种尺度有限元计算模型,其整体网格划分及桩与周围土体的局部网格型式如图2 所示。其中数字①~⑤表示抗滑桩-边坡计算模型尺度(宽度)不同,依次代表单桩取半(计算模型宽度为0.5S,桩取半桩)、单桩(计算模型宽度为1S,取全桩)、双桩取半(计算模型宽度为1S,取两个半桩)、双桩(计算模型宽度为2S,取两个全桩)、单桩加双桩取半(计算模型宽度为2S,取两个半桩加一个全桩)。为了减小接触面单元的病态条件,抗滑桩周围土体采用较细的网格形式,土与桩的单元形式皆采用六面体减缩积分。所有模型采用统一的边界条件,即边坡两侧面Z 方向水平位移约束,前后两面X 方向水平位移约束,底面X、Y、Z 方向全约束。
利用强度折减有限元法计算加固前边坡(模型宽度Z =3.0~16.0 m)的安全系数为1.158~1.162,与Cai 等[10]、Won 等[12]和Wei 等[13]所得的安全系数1.13~1.20 基本一致,微小的差别可能源于有限元网格、数值算法、失稳判据等因素。考虑采用抗滑桩加固方案,有关参数同前,分别计算了5 种尺度有限元模型下的边坡安全系数,所得结果列于表2。

图2 5 种尺度有限元计算模型及网格形式 Fig.2 Five computational models and the FE meshes
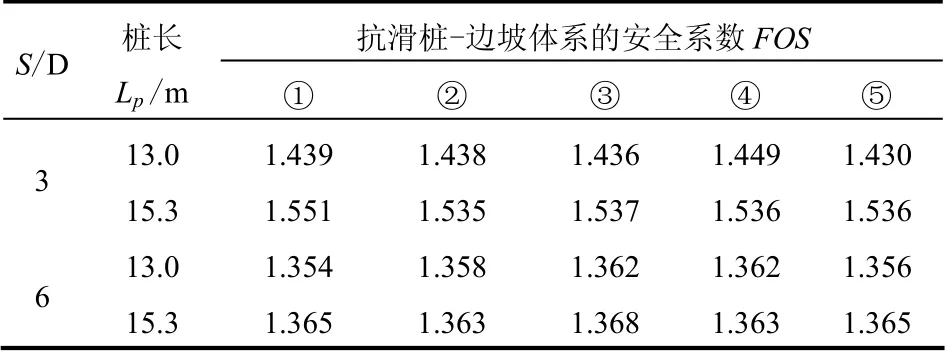
表2 5 种尺度有限元计算模型下的边坡安全系数 Table 2 FOS of slope with a row of piles under five models
分析表2 可知,当桩间距与桩径之比S/D 和桩长(Lp)一定时,5 种尺度计算模型所得边坡的安全系数基本相同,相对误差不超过3%,说明在计算桩-边坡体系安全系数时,有限元计算模型尺度取0.5S、1S(两个半桩或全桩)和2S(两个全桩或两个半桩加一个全桩),所得安全系数并无差异;所不同的是,在网格大小划分一致的情况下,桩-边坡体系计算模型尺度取0.5S 时计算工作量将大大减少,这在很大程度上提高了三维数值计算的效率。
为进一步验证上述结论的正确性,将抗滑桩的弹性模量调整为60 000 MPa,土的变形模量调整为200 MPa,计算了桩间距S 为3.0 m,桩径D 为0.8 m和1.0 m 时的桩-边坡体系安全系数,结果列于表3。

表3 修改材料参数后桩-边坡体系的安全系数 Table 3 FOS of slope with piles after modified parameters
分析表3 同样可以得出前述结论,即5 种尺度计算模型在相同参数条件下所得边坡安全系数相同。特别地,当桩径为D =0.8 m 时,加固边坡的安全系数为1.730,与Wei 等[13]利用有限差分法所得结果1.72 相一致,从而验证了上述方法的可行性。
此外,分析表3 还可发现,不同的桩底接触模式(接触与固定模式)对抗滑桩加固边坡的安全系数有一定的影响,固定模式下的安全系数明显大于接触模式;对比表2、3 可见,提高桩与土的弹性模量,边坡的安全系数也在一定程度上得到改善,桩的抗弯刚度增加,一定程度上提高了抗滑效果。
4 最佳设桩位置问题
利用前述边坡算例,取桩间距为S =3.0、4.0、5.0 m,改变抗滑桩在坡体中的位置,使Lx从0 变化到15.0 m,所得安全系数随Lx与坡面水平长度L比值的变化曲线如图3 所示。分析这3 条曲线,当设桩于Lx=7.5 m 处,即坡中位置,桩-边坡体系获得最大的安全系数;当设桩于坡顶或坡脚处,安全系数略高于无桩状态,但提高幅度不显著。进一步采用二次抛物线对3 条曲线进行拟合,得到相应的抛物线方程,如图3 中所示,其对称轴位于Lx/L=0.5处,说明在该处边坡加固效果最好;当桩间距比S/D较小时(图中S/D =3)抛物线开口较小,不同设桩位置处的安全系数明显高于桩间距比S/D =4 和5 时的情况(抛物线趋于平缓),说明桩间距比影响着加固边坡的安全系数。
图4 显示抗滑桩不同加固位置时的边坡临界滑动面。对比分析可见,当抗滑桩位于边坡中部时,其滑裂面以桩为界被分为前、后两个部分,起到了最有效的阻滑作用,这与无桩状态下临界滑裂面反映出的边坡中部出现高应变区是一致的;而设桩于坡顶与坡脚附近时,滑裂面基本为一条圆弧形的曲面,抗滑桩的阻滑作用并不明显。

图3 安全系数随桩加固位置的变化曲线 Fig.3 Effects of pile location on FOS

图4 不同设桩位置时边坡的临界滑裂面 Fig.4 Critical slip surface at the different pile location
5 合理桩间距与桩径比问题
仍采用前述算例参数,改变桩间距S 值,得到不同桩间距与桩径比S/D(以下简称间距比)条件下边坡的安全系数变化曲线,如图5 所示。随着间距比S/D 增大,安全系数逐渐减小并趋于无桩状态;当S/D≤6 时,边坡安全系数随间距比S/D 的增大而大幅减小,这说明抗滑桩的群桩效应在快速减弱;当S/D>6 时,随着S/D 增加,边坡安全系数小幅下降并趋于无桩状态,这反应群桩效应已不明显,只有单桩在起阻滑作用[16]。

图5 安全系数随桩间距比变化曲线 Fig.5 Effect of ratio of pile spacing to pile diameter on FOS
图6 显示不同桩间距比S/D 条件下的边坡临界滑裂面。其中图6(a)、(c)、(e)和(g)显示过桩中心线的截面,图6(b)、(d)、(f)和(h)显示两桩之间的中心截面,其中z=0 为过桩形心的剖面,z=1、2、3、4 m分别为不同S/D 时过两桩中心的剖面。分析图6(b)可见,当S/D =2 时,滑裂面以桩为界被分为前、后2 个部分,此时抗滑桩发挥挡墙的功效;当S/D =4时,群桩效应已发挥,桩间有土拱产生,如图6(d);而图6(f)、(h)表明,当S/D≥6 边坡破坏时,其临界滑裂面为一条连续贯通的圆弧形曲面,且滑裂面的深度基本相同,说明桩与桩间的相互作用减弱,土拱效应已接近消失,这与图5 结果是一致的。
变化桩径D 从0.6 m 到2.0 m,考察安全系数随桩径的变化关系,所得曲线如图7 所示。当桩间距为S =3.0 m 时,随着桩径的增大,安全系数呈线性增长。间距比S/D 不变时,桩径在0.6~2.0 m 之间变化(不考虑弹性模量的变化)所得安全系数基本相同,说明抗滑桩加固边坡工程,根据预期的安全系数,桩间距与桩径有多种可供选择方案。
6 合理桩长问题
采用算例参数,考察桩长Lp从4.3 m 到15.3 m变化时边坡的安全系数,所得结果绘于图8。

图6 不同间距比条件下的边坡临界滑裂面 Fig.6 Effect of ratio of pile spacing to pile diameter on CSS

图7 安全系数随桩径变化曲线 Fig.7 Effect of pile diameter on FOS

图8 安全系数随桩长的变化曲线 Fig.8 Effect of pile length on FOS
分析图8 可见,随着桩长增加,边坡安全系数不断增大;当桩长4.3≤Lp≤7.3 m 时,安全系数呈线性变化关系;而当Lp>7.3 m 时,曲线斜率突然变大,边坡安全系数显著提高;但当桩长小于4.3 m时无法改善边坡的稳定性,因为此时桩长小于临界滑动面深度,这从图9 中临界滑动面深度hc=4.3 m 可反映出。进一步分析图9,当桩长Lp≤7.3 m 时,塑性应变剪切带最深处基本都通过桩底,说明加固效果不理想;当Lp>7.3 m 后,塑性应变剪切带沿桩周发展,而没有扩展至桩底,由此表明,抗滑桩已起到明显的抗滑效果;这与图8 显示的当桩长Lp≥7.3 m 时安全系数显著增加(曲线斜率明显增大)的变化趋势是一致的,由此可将此时的桩长 7.3 m作为设计桩长,相当于锚固深度为2/5桩长(临界滑动面深度为hc=4.3 m),这与抗滑桩设计手册[20]中建议的土质边坡抗滑桩锚固深度约为1/3~1/2 桩长是一致的。
7 桩头约束效应问题
考虑4 种桩头约束条件[5,10],即自由桩头(可任意转动和位移)、无转动桩头(可无转动地发生位移)、铰接桩头(无位移地转动)和固定桩头(无转动也无位移),利用算例边坡中的桩土参数,分别计算桩底接触模式(Lp=13.0 m)与固定模式(Lp= 15.3 m)情况下的桩身弯矩、剪力及桩侧位移、土压力分布,所得固定模式结果如图10 所示。
从图可见,铰结和固定桩头条件下桩身的弯矩较小,在8.0 m 以下(嵌岩段)桩身弯矩分布更小,表明约束桩头位移,能有效减小桩身弯矩,并使之分布趋于合理,充分发挥抗滑潜力;而不转动和自由桩头条件下桩身弯矩相对较大。对比2 种不同桩底接触模式下的弯矩或剪力图可见,桩底接触模式的选取对桩身最大弯矩和剪力的影响较小,而对其沿桩身的分布模式有一定影响;桩底固定模式下的桩身位移和桩侧土压力,总体上小于桩底接触模式。

图9 不同桩长时边坡的临界滑裂面 Fig.9 Critical slip surface at different pile lengths
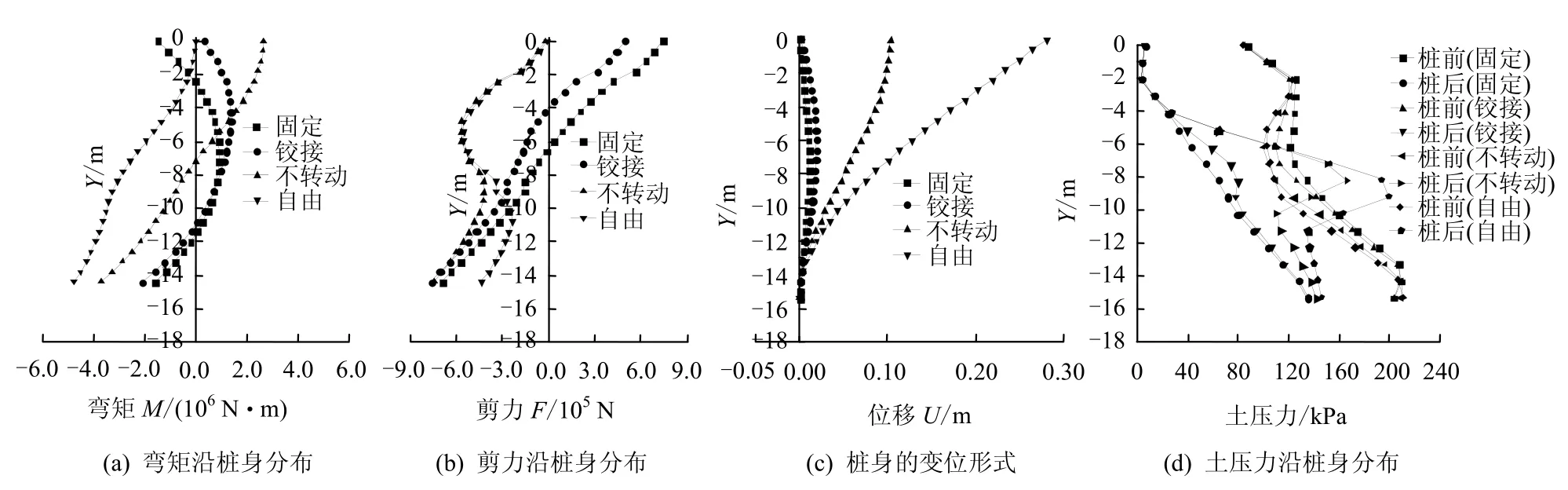
图10 桩底固定模式下的桩身内力及变位 Fig.10 Behavior of pile with fixed mode under four boundary conditions
8 结 论
(1)三维有限元数值计算中,单桩取半、单桩、双桩取半、双桩、单桩加双桩取半5 种尺度计算模型所得边坡的安全系数并无差异;所不同的是,在网格大小划分一致的情况下,桩-边坡体系计算模型尺度取0.5S 时的计算工作量大大减少,效率倍增;
(2)抗滑桩加固于边坡中部可获得最大的安全系数,而位于坡顶或坡脚处所得安全系数略高于无桩状态,总体上其安全系数与设桩位置的变化曲线近似为一抛物曲线;
(3)抗滑桩加固边坡的安全系数随桩间距与桩径之比S/D 的增加而减小,最优间距比宜为S/D =2~6,此时桩间存在土拱效应;间距比S/D 不变情况下,增加桩径安全系数基本不变;而桩间距S不变,增加桩径D,则安全系数呈线性增加;均质土坡中抗滑桩设计桩长宜为2.5倍临界滑动面深度。
(4)本文所得结论适用于直线型均质土坡,对于其他几何形状和荷载条件的复杂边坡,仍需开展进一步的研究工作。
[1] 陈立新, 王士川. 抗滑桩的弹塑性理论分析[J]. 工业建筑, 1997, 27(7): 28-33. CHEN Li-xin, WANG Shi-chuan. The analysis of elastic-plastic design theory of anti-slide piles[J]. Industrial Construction, 1997, 27(7): 28-33.
[2] ITO T, MATSUI T. Methods to estimate lateral force acting on stabilizing piles[J]. Soils and Foundations, 1975, 15(4): 43-59.
[3] ITO T, MATSUI T, HONG W P. Design method for stabilizing piles against landslide—one row of piles[J]. Soils and Foundations, 1981, 21(1): 21-37.
[4] ITO T, MATSUI T, HONG W P. Extended design method for multi-row stabilizing piles against landslide[J]. Soils and Foundations, 1982, 22(1): 1-13.
[5] HASSIOTIS S, CHAMEAU J L, GUNARATNE M. Design method for stabilization of slopes with piles[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1997, 123(4): 314-323.
[6] 周德培, 肖世国, 夏雄. 边坡工程中抗滑桩合理桩间距的探讨[J]. 岩土工程学报, 2004, 26(1): 132-135. ZHOU De-pei, XIAO Shi-guo, XIA Xiong. Discussion on rational spacing between adjacent anti-slide piles in some cutting slope projects[J]. Chinese Journal of Geotechnical Engineering, 2004, 26(1): 132-135.
[7] 张建勋, 陈福全, 简洪钰. 被动桩中土拱效应问题的数值分析[J]. 岩土力学, 2004, 25(2): 174-178. ZHANG Jian-xun, CHEN Fu-quan, JIAN Hong-yu. Numerical analysis of soil arching effects in passive piles[J]. Rock and Soil Mechanics, 2004, 25(2): 174-178.
[8] 吕庆, 孙红月, 尚岳全. 抗滑桩桩后土拱形状及影响因素[J]. 哈尔滨工业大学学报, 2010, 42(4): 629-633. LÜ Qing, SUN Hong-yue, SHANG Yue-quan. Shape of soil arch behind anti-slide piles and its major influence factors[J]. Journal of Harbin Institute of Technology, 2010, 42(4): 629-633.
[9] 赵明华, 廖彬彬, 刘思思. 基于拱效应的边坡抗滑桩桩间距计算[J]. 岩土力学, 2010, 31(4): 1211-1216. ZHAO Ming-hua, LIAO Bin-bin, LIU Si-si. Calculation of anti-slide piles spacing based on soil arching effect[J]. Rock and Soil Mechanics, 2010, 31(4): 1211-1216.
[10] CAI F, UGAI K. Numerical analysis of the stability of a slope reinforced with piles[J]. Soils and Foundations, 2000, 40(1): 73-84.
[11] LIANG R, ZENG S. Numerical study of soil arching mechanism in drilled shafts for slope stabilization[J]. Soils and Foundations, 2002, 42(2): 83-92.
[12] WON JINOH, YOU KWANGHO, JEONG SANGSEOM, et al. Coupled effects in stability analysis of pile-slope systems[J]. Computers and Geotechnics, 2005, 32(4): 304-315.
[13] WEI W B, CHENG Y M. Strength reduction analysis for slope reinforced with one row of piles[J]. Computers and Geotechnics, 2009, 36(7): 1176-1185.
[14] 高长胜, 陈生水, 杨守华, 等. 基于强度折减有限单元法的抗滑桩加固边坡特性分析[J]. 水利与建筑工程学报, 2010, 8(4): 119-122. GAO Chang-sheng, CHEN Sheng-shui, YANG Shou-hua, et al. Analysis for slope stability reinforced with anti-slide piles based on strength reduction method with3D FEM[J]. Journal of Water Resources and Architectural Engineering, 2010, 8(4): 119-122.
[15] DANIEL PRADEL, JASON GARNER, ANNIE ON LEI KWOK. Design of drilled shafts to enhance slope stability[C]//Proceedings of 2010 Earth Retention Conference. Los Angeles: [s. n.], 2010: 920-927.
[16] KOURKOULIS R, GELAGOTI F, ANASTASOPOULOS I, et al. Slope stabilizing piles and pile-groups: parametric study and design insights[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2011, 137(7).doi: 10.1061/(ASCE)GT.1943-5606. 0000479.
[17] 杨明, 姚令侃, 王广军. 桩间土拱效应离心模型试验及数值模拟研究[J]. 岩土力学, 2008, 29(3): 817-822. YANG Ming, YAO Ling-kan, WANG Guang-jun. Study of centrifuge model tests and numerical simulation on soil arching in space of piles[J]. Rock and Soil Mechanics, 2008, 29(3): 817-822.
[18] 高长胜, 魏汝龙, 陈生水. 抗滑桩加固边坡变形破坏特性离心模型试验研究[J]. 岩土工程学报, 2009, 31(1): 145-148. GAO Chang-sheng, WEI Ru-long, CHEN Sheng-shui. Centrifugal model tests on deformation of slopes reinforced with piles[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(1): 145-148.
[19] 年廷凯. 桩-土-边坡相互作用数值分析及阻滑桩简化设计方法研究[D]. 大连: 大连理工大学, 2005.
[20] 铁道部第二勘测设计院. 抗滑桩设计与计算[M]. 北京: 中国铁道出版社, 1983.

