反演法设计磁共振射频阵列线圈的研究

张战胜 辛学刚

（南方医科大学生物医学工程学院，广州 5 10515）

引言

磁共振成像（magnetic resonance imaging，MRI）是当今医学领域发展最快、最具潜力的一种成像技术。MRI具有较高的信噪比与空间分辨率，且对受检病人无电离辐射危害，已经成为临床医学影像检查最重要的手段之一。MRI系统主要由磁体系统、梯度系统、射频线圈、谱仪和计算机系统组成，其中射频线圈的主要功能是发射射频脉冲，使磁化的质子吸收能量产生共振，并接收质子在弛豫过程中释放的能量，从而产生MR信号。射频线圈是MRI系统拾取信号的核心部件，其优劣将决定MRI的成像质量，所以射频线圈的设计是MRI领域研究的重点［1］。

在MRI系统中，射频线圈按照用途可以分为射频发射线圈和射频接收线圈两种。射频发射线圈要求在ROI（region of interest）内产生均匀的电磁场，确保ROI内产生相同强度的MR信号，同时要求ROI内磁场强度满足目标磁场强度的要求，射频发射效率高；射频接收线圈要求线圈以相同的增益接收ROI内不同位置产生的MR信号，同时线圈接收信号的信噪比（signal-to-noise，SNR）高低也是衡量射频接收线圈性能优劣的重要标准。在临床应用中，一般采用两种射频线圈：容积线圈作为发射线圈在ROI内产生均匀的电磁场，同时用表面线圈接收ROI内的MR信号，而阵列线圈能同时满足发射线圈的磁场均匀性和接收线圈的高信噪比要求。因此，随着阵列线圈技术的出现，射频线圈的研究设计得到了很大的发展。

Roemer结合容积线圈和表面线圈的优点设计出阵列线圈，它由两个或两个以上小线圈或线圈单元组成线圈阵列［2］。每个小线圈可以同时接收各个区域的信号并有机地结合起来，每个小线圈中的噪声仅来源于对应的小区域，所以阵列线圈获得的磁共振信号是各个小线圈获得信号的加权和，但噪声仅来源于各个小线圈所对应的小区域，所成图像的信噪比较高。因此，射频阵列线圈的研究成为MRI技术领域的一个重要方向［3－5］。

目前的射频阵列线圈都是面向躯干的通用线圈，临床应用中阵列线圈产生的射频场B1均匀、获得图像的信噪比高，同时也能够获得较大的视野（field of view，FOV），但是无法强化局部ROI内射频场B1的均匀性及强度，弱化其他区域。近年来，术中MRI是新的发展方向，需要面向器官的射频线圈，强化特定ROI内的磁场分布，弱化其他区域的磁场强度。显然，常规的射频线圈设计方法只能满足术中磁共振的部分需求，需要面向ROI设计的射频线圈才能满足临床诊断的特殊要求［6－7］。反演法从需求的目标电磁场出发，结合目标器官的位置和目标磁场分布，倒推出射频线圈的结构，因此对于设计有特定应用目的的射频线圈非常有实用价值［8］。

反演法设计射频阵列线圈首先给定ROI内的磁场分布，然后求解能够产生该分布的射频电流分布。Turner提出目标场法（target field method）［9］，根据ROI内的磁场分布，利用傅里叶变换和贝塞尔函数建立方程组，得到相应的电流密度表达式。然而，该方法有一定的局限性，需要先假设电流分布在无限长的导线上，才能进行相应的傅里叶逆变换。Forbes et al利用积分函数求解得到电流密度表达式，解决了射频电流源无限长约束的问题［10］。Lawrence et al提出用全波时域法（full-wave timeharmonic approach）设计射频线圈轮廓的方法［11］，用傅里叶级数和时域格林函数求解，得到能够在ROI内产生目标磁场的电流分布，然而在求解过程中会出现积分高病态问题，需要应用正则化技术优化才能得到满足理论要求的射频线圈轮廓［12－13］。

以往用反演法设计射频线圈，ROI都设定在中心位置，无法满足临床诊断的不同需求。本研究以反演法为基础，结合傅里叶逆变换、时域格林函数，设计ROI在任意位置的磁共振射频阵列发射线圈；针对求解电流密度过程中出现的积分函数高病态问题，采用最小功率正则化技术进行优化，应用流函数技术成功获得了射频阵列发射线圈的轮廓图；通过对阵列线圈在ROI内的磁场分布与目标磁场比较，验证了反演法设计任意位置ROI磁共振射频阵列发射线圈的适用性和实用性。

1 理论与方法

1.1 理论模型

首先，假设阵列线圈电流分布在半径为b、长2L的圆柱形结构表面如图1所示，圆柱以z轴为方向轴，以z=0为中心，圆柱表面的电流密度为J。ROI为圆心（ra，θa，za），半径r的球形区域，ROI内的目标磁场为HT（target H-field）。圆柱表面的电流分布决定ROI内的磁场分布，本研究的主要目的是应用反演法去设计能够在ROI内产生目标磁场强度的阵列线圈。

变化的电场和磁场相互联系、相互激发，形成统一的电磁场，由麦克斯韦方程组和格林函数得到ROI内时变电磁场表达式［14］为

由式 (1)～式(3)，可以得到在 ROI表面任意点 (r，θ，z)沿 x轴、y轴方向的磁场强度，即

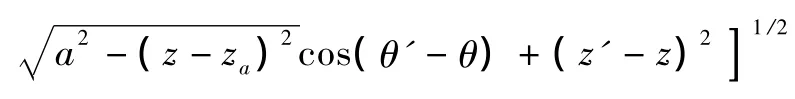
1.2 求解与正则化

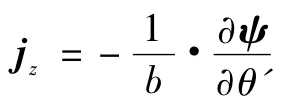
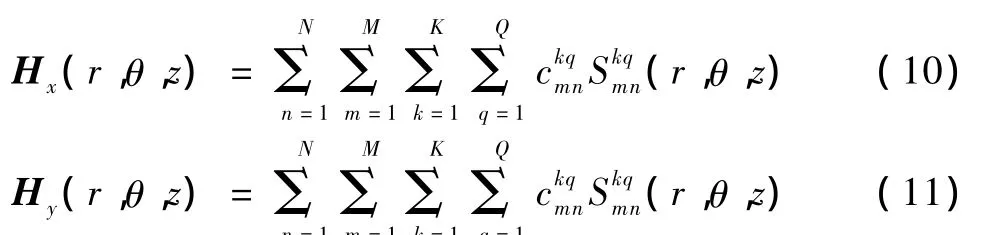
式中

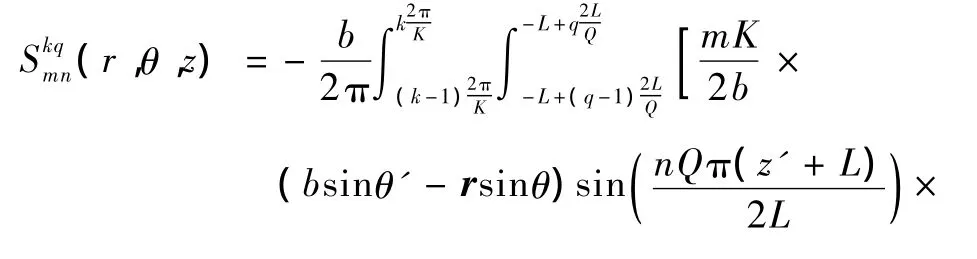
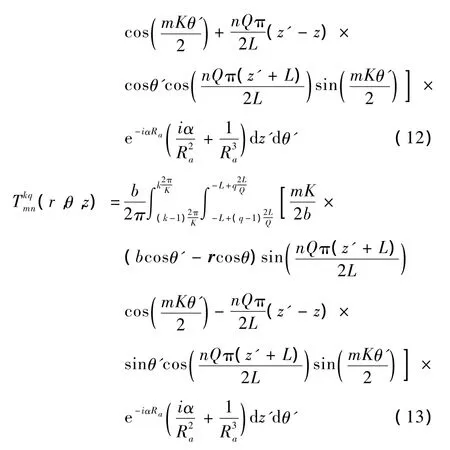
为了求解能够在ROI内产生目标磁场的电流分布，ROI内的磁场与目标磁场必须满足

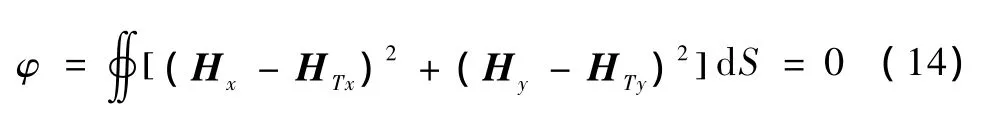
式中，HTy和HTx分别表示ROI内zox平面和zoy平面上的目标磁场强度，该积分公式的作用区间为ROI表面。

结合式（10）～（11）及（14）的求解，就可以得1到任意子区域（k，q）的电流密度未知系数（m=：M，n=1：N，k=1：K，q=1：Q），如要求解系数（u=1：M，v=1：N，f=1：K，g=1：Q），式（14）必须满足

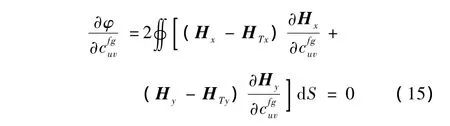
在反演法设计磁共振梯度线圈或射频线圈的过程中，为了优化求解中出现的高病态问题，主要采用的补偿函数有最小电感、最小储能和最小功率［18－20］。在设计阵列线圈过程中，采用最小功率正则化技术，优化求解中的高病态问题，最小功率补偿函数为

式中，ψ*（θ'，z'）是ψ（θ'，z'）的复共轭函数，ψS（θ'，z'）的等势线就是阵列线圈的轮廓图。

通过式（10）～式（11），检验该阵列线圈在ROI内的磁场是否满足目标磁场的要求。

图2 球形ROI表面均匀分布的采样点Fig.2 The sample points distributed on the surface of the ROI

2 结果与讨论

根据上面的论述，设定阵列线圈模型的中心点位于柱坐标系的原点，x、y和z轴方向如图1所示，阵列线圈的圆柱模型长度2L=25 cm，半径b=10 cm。在临床应用中，ROI内的磁场强度量级为50 μΤ［21］，设计的阵列线圈在ROI内的磁场强度与目标磁场强度的误差在5％以内（数量级小于10－6T）就满足目标磁场的要求［22］。设定ROI内的目标磁场为均匀的线性极化场（HTx（r，θ，z）=1 A/m，HTy（r，θ，z）=1 A/m），磁共振频率为128 MHz（3 T）。为了设计满足理论要求的阵列线圈，需通过反复的迭代计算确定正则化参数λ，式（8）～式（9）中的傅里叶级数M=N=9。在求解过程中，利用Matlab工具编程实现积分计算，建立矩阵和求解，标绘阵列线圈的轮廓图，以及计算射频线圈在ROI内的磁场分布。

首先设计线圈阵列（K×Q）=（2×1）、ROI中心（ra，θa，za）=（0，0，0）、半径a=5 cm的阵列线圈，在ROI表面取360个均匀分布的采样点，如图2所示。通过仿真计算，可知矩阵A的条件数为1021，是高病态的，需要用正则化技术进行优化。综合考虑ROI内的磁场强度和目标磁场强度的误差及最小功率需求，可知正则化参数λ必须通过反复迭代计算得到最优解。在引入正则化参数λ=10－11优化后，矩阵A的条件数为1011，高病态问题得到了很好的解决。为更好地比较实验结果，设计了（K×Q）=（4×3）的阵列线圈，优化前矩阵的条件数为1023，通过迭代计算正则化参数λ=10－13，优化后矩阵的条件数为1013。求解得到射频线圈轮廓图，并观察比较两种阵列的射频线圈在ROI内的磁场分布是否满足目标磁场的要求。

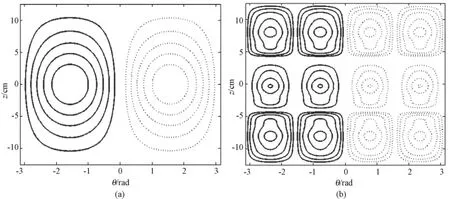
图3 ROI中心对称的阵列线圈轮廓，虚线表示反向电流。（a）（2×1）阵列；（b）（4×3）阵列Fig.3 Contour plots of the phased array coil with a symmetrically located ROI，the dashed lines mean inverse current.（a）（2×1）array；（b）（4×3）array

利用Matlab工具得到射频线圈绕组轮廓，如图3所示。图3（a）和（b）分别表示（2×1）阵列和（4×3）阵列线圈绕组的轮廓，红色虚线表示反向电流。在临床应用中，为了获得较好的MR信号，要求射频线圈在ROI内的磁场分布均匀，磁场强度满足目标磁场的要求，因此射频线圈在ROI内的磁场均匀性以及磁场强度大小是判断射频线圈优劣的主要依据。为了验证设计结果的准确性，计算射频线圈在ROI内的磁场分布，如图4所示。观察比较图4可知，（2×1）阵列和（4×3）阵列的射频线圈在ROI内的磁场分布都比较均匀，ROI磁场强度在0.98 A/m以上，满足目标磁场强度的要求。在ROI边界（4×3）阵列射频线圈的均匀性优于（2×1）阵列射频线圈，说明随着线圈阵列的增多，阵列线圈在ROI内的磁场分布均匀性较好，磁场强度满足目标磁场强度的要求。

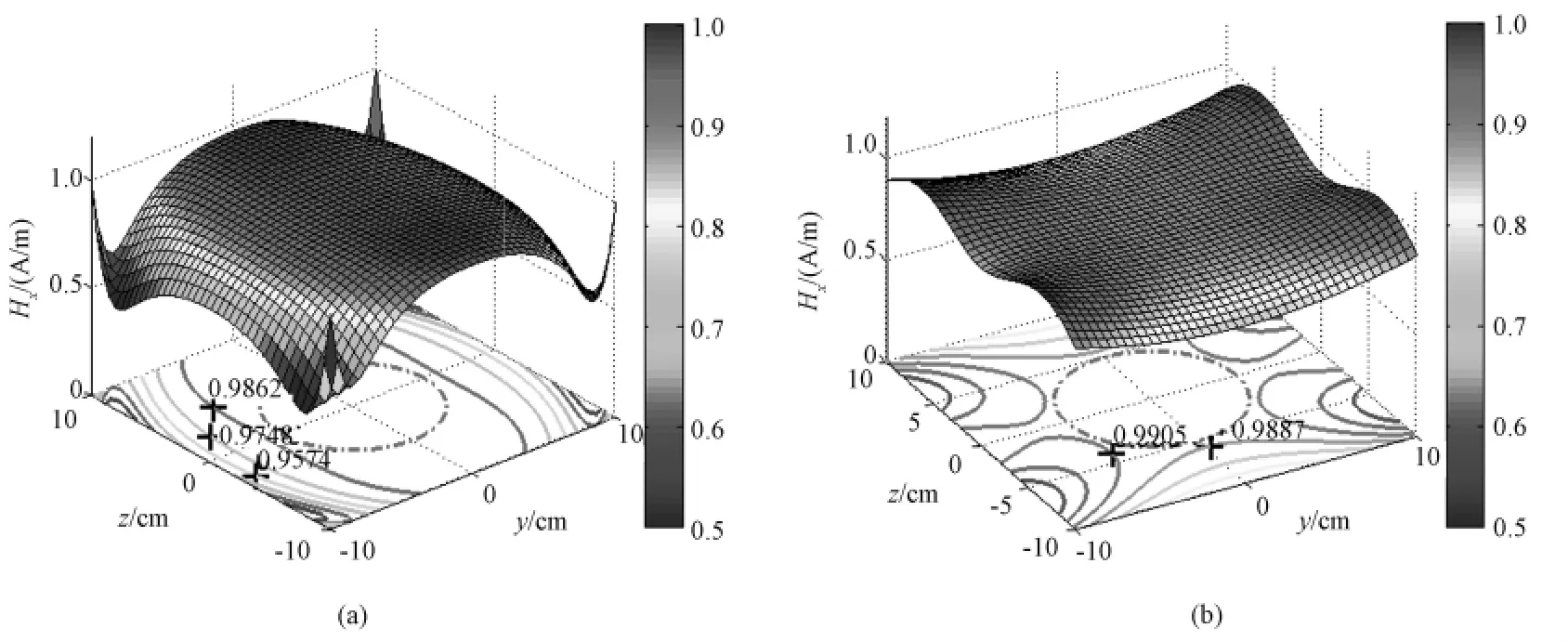
图4 射频线圈（见图3）在ROI内zoy平面上的Hx（r，θ，z）分布。（a）（2×1）阵列；（b）（4×3）阵列Fig.4 The induced magnetic field Hx（r，θ，z）along zoy plane within the ROI of Fig.3，the dashed line means ROI.（a）（2×1）array，（b）（4×3）array

通过以上分析，运用反演法设计ROI对称的阵列线圈，能很好地满足目标磁场的要求，但是针对不同的临床需要，ROI的位置是不同的，所以进一步考虑了ROI不是轴对称的情况，设计了ROI中心（ra，θa，za）=（0，0，5）、半径a=5 cm、子区域分别为（2×1）阵列和（4×3）阵列的两种射频线圈。针对高病态问题，正则化参数分别为λ=10－12和λ=10－14，阵列线圈绕组轮廓分布如图5所示。与图4比较发现，随着ROI中心向z轴移动，线圈轮廓的分布也随之移动，整体分布情况大体相似。

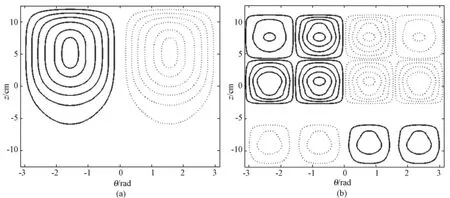
图5 ROI轴不对称的阵列线圈轮廓，虚线表示反向电流。（a）（2×1）阵列；（b）（4×3）阵列Fig.5 Contour plots of the phased array coil with an axially asymmetrically located ROI，the dashed lines mean inverse current.（a）（2×1）array；（b）（4×3）array

计算该射频线圈在ROI内的磁场分布情况，如图6所示。比较发现，（2×1）阵列和（4×3）阵列的射频线圈在ROI内的磁场分布基本均匀，但是在ROI边缘的磁场均匀性下降，强度也不再满足目标磁场的要求。显然，如果减小ROI的半径，可以很好地解决这方面的问题。计算ROI位置相同半径a=2.5 cm、阵列为（4×3）的射频线圈在ROI内的磁场分布，如图7所示。与图6（c）和（d）相比，随着半径的减小，ROI内的磁场均匀性及强度都有很大的提高，能很好地满足目标磁场的要求。

在临床检查中，ROI的位置除了中心对称和轴不对称外，还存在其他很多复杂的情况，譬如在心脏、脊柱以及肝脏的MRI检查中，ROI远离中心轴位置。为更好地验证反演法在阵列线圈设计中的适用性，考虑了ROI中心远离z轴的情况，（ra，θa，za）=（5，π/2，0），半径a=2.5 cm。为了便于结果比较，同时设计子区域分别为（2×1）和（4×3）的两种射频阵列发射线圈，优化参数分别为λ=10－14和λ=10－16，两种子区域阵列线圈的轮廓如图8所示，计算射频线圈在ROI内的磁场分布情况如图9所示。比较发现，ROI中心为（ra，θa，za）=（5，3/2，0）时，（2×1）和（4×3）阵列线圈在ROI内的磁场分布均匀性都比较好，磁场强度也满足目标磁场的强度要求。

本研究分别设计了ROI位置不同和线圈阵列不同的射频发射线圈，通过比较分析各个线圈在ROI内的磁场分布情况，发现对于相同的ROI，不同阵列的射频线圈在ROI内的磁场分布随着线圈阵列的增多性能越好，当ROI中心偏向z轴或偏离对称轴时，ROI的半径越小，阵列线圈在ROI内的磁场分布越好，磁场强度也越符合目标磁场的要求。因此，在应用反演法设计射频阵列发射线圈的过程中，要综合考虑ROI的位置、半径大小以及线圈阵列数的要求，有针对性地设计满足不同临床需求的MR射频阵列发射线圈。

3 结论

本研究探讨了反演法在磁共振射频阵列发射线圈设计中的应用，将柱形线圈模型划分成多个子区域，用傅里叶级数表达出每个子区域内的电流密度，针对求解过程中出现的高病态问题，采用最小功率正则化技术进行优化，然后应用流函数技术求解出符合要求的阵列线圈轮廓。为了满足不同的临床诊断需求，比较了ROI位置不同的几种阵列发射线圈。实验结果表明，以反演法为基础设计的射频阵列发射线圈，在ROI内的磁场分布均匀，磁场强度符合理论设计要求；证明了反演法在射频阵列发射线圈设计中的适用性和实用性，为MR射频线圈的设计提供了一种新方法和理论依据。

图6 射频线圈（见图5）在ROI内的磁场分布。（a）（2×1）阵列线圈在zoy平面上的Hx（r，θ，z）分布；（b）（2×1）阵列线圈在zox平面上的Hy（r，θ，z）分布；（c）（4×3）阵列线圈在zoy平面上的Hx（r，θ，z）分布；（d）（4×3）阵列线圈在zox平面上的Hy（r，θ，z）分布Fig.6 The induced magnetic field within the ROI of Fig.5，the dashed line means ROI.（a）the induced Hx（r，θ，z）along zoy plane of（2×1）array；（b）the induced Hy（r，θ，z）along zox plane of（2×1）array；（c）the induced Hx（r，θ，z）along zoy plane of（4×3）array；（d）the induced Hy（r，θ，z）along zox plane of（4×3）array

图7 ROI中心（ra，θa，za）=（5，π/2，0）、半径a=2.5 cm、子区域为（4×3）阵列的射频线圈在ROI内的磁场分布。（a）zoy平面上的Hx（r，θ，z）分布；（b）zox平面上的Hy（r，θ，z）分布Fig.7 The induced field of the（4×3）array RF coil within the ROI of radius a=2.5 cm.（a）the induced Hx（r，θ，z）along zoy plane；（b）the induced Hy（r，θ，z）along zox plane

图8 ROI半径不对称的阵列线圈轮廓，虚线表示反向电流。（a）（2×1）阵列；（b）（2×1）阵列Fig.8 Contour plots of the phased array coil with a radially asymmetrically located ROI，the dashed lines mean inverse current.（a）（2×1）array；（b）（2×1）array

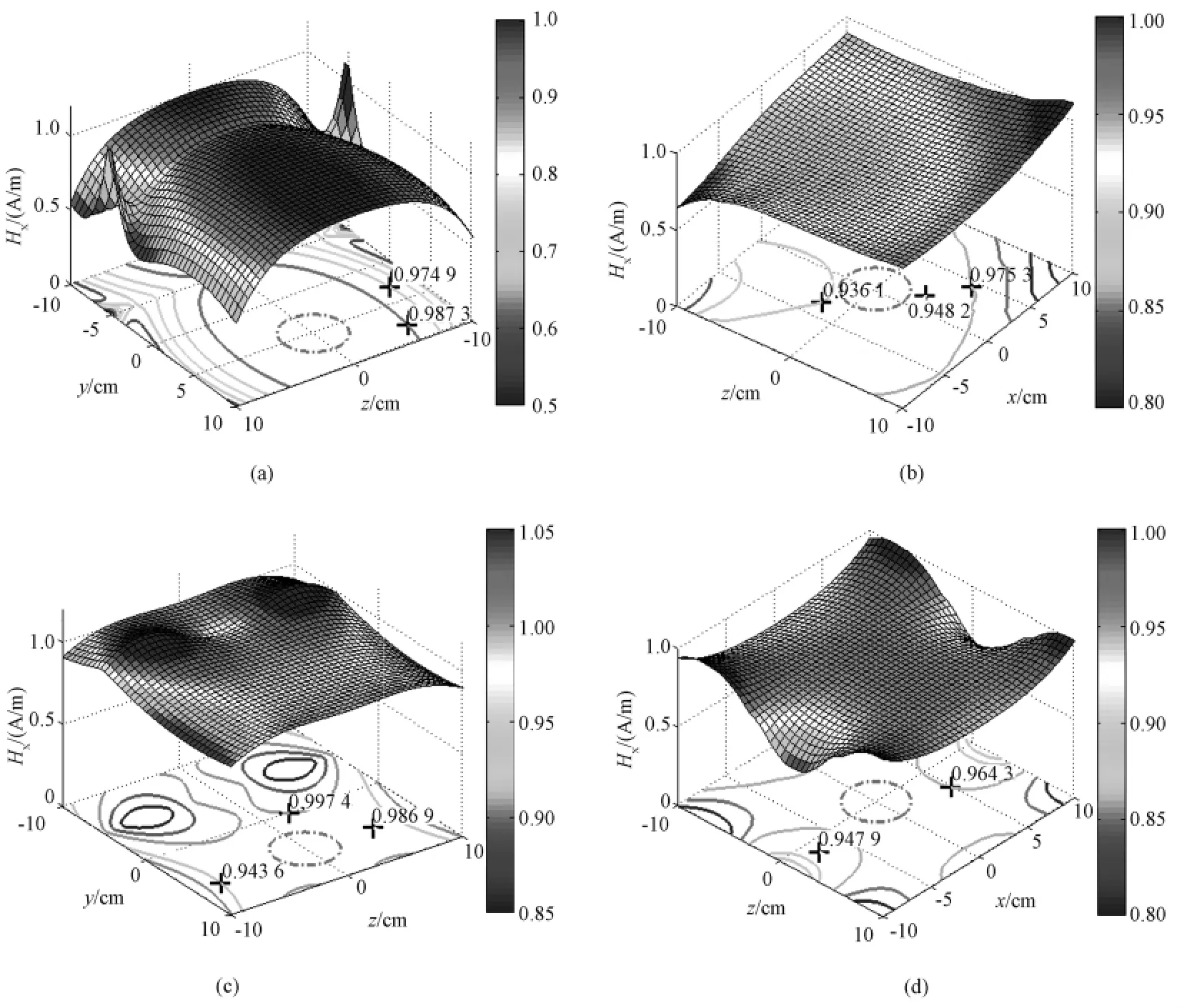
图9 射频线圈（见图8）在ROI内的磁场分布。（a）（2×1）阵列线圈在zoy平面上的Hx（r，θ，z）分布；（b）（2×1）阵列线圈在zox平面上的Hy（r，θ，z）分布；（c）（4×3）阵列线圈在zoy平面上的Hx（r，θ，z）分布；（d）（4×3）阵列线圈在zox平面上的 Hy（r，θ，z）分布Fig.9 The induced magnetic field within the ROI of Fig.8，the dashed line means ROI.（a）the induced Hx（r，θ，z）along zoy plane of（2×1）array；（b）the induced Hy（r，θ，z）along zox plane of（2×1）array；（c）the induced Hx（r，θ，z）along zoy plane of（4×3）array；（d）the induced Hy（r，θ，z）along zox plane of（4×3）array

在研究过程中，忽略了阵列线圈之间的相互耦合作用以及线圈和负载之间的相互影响，因此本课题组正在开展这方面的相关研究工作。

［1］赵喜平.磁共振成像系统的原理及其应用［M］.北京：科学出版社，2000：216－225.

［2］Roemer PB，Edelstein WA，Hayes CE，et al.The NMR Phased Array［J］.Measurement Science and Technology.1990，16（2）：192－225.

［3］Ying，Leslie，Liang Zhipei.Parallel MRI using phased array coils［J］.IEEE Signal Processing Magazine，2010，2（4）：90－98.

［4］Sani F，Foresti M，Parmiggiani A，et al.3-T MRI with phasedarray surface coil in the local staging of rectal cancer［J］.Radiol Med，2011，116：375－388.

［5］Janssens T，Keil B，Farivar R，et al.An implanted 8-channel array coilforhigh-resolution macaqueMRIat 3T［J］.NeuroImage，2012，62（3）：1529－1536.

［6］韩继钧，辛学刚，冯衍秋，等.磁共振引导下术中开放式多通道射频接收线圈设计［J］.中国生物医学工程学报.2011，30（1）：75－81.

［7］Xin Xuegang，Feng Yanqiu，Han Jijun，et al.Three-channel receive-only RF coil for vertical-field MR-guided focused ultrasound surgery［J］.Concepts in Magnetic Resonance Part B：Magnetic Resonance Engineering，2010，37B（4）：237－244.

［8］Xin Xuegang，Han Jijun，Feng Yanqiu，et al.Inverse design of an organ-oriented RF coil for open，vertical-field，MR-guided，focused ultrasound surgery［EB/OL］.http：//dx.doi.org/10.1016/j.mri.2012.05.009，2012-06-15/2012-07-01.

［9］Turner R.A target field approach to optimal coil design［J］.Journal of Physics D：Applied Physics，1986，19（8）：L147-L151.

［10］Forbes LK，Brideson MA，Crozier S.A target-field method to design circular biplanar coils for asymmetric shim and gradient fields［J］.IEEE Transactions on Magnetics，2005，41（6）：2134－2144.

［11］Lawrence BG，Crozier S，Yau DD，et al.A time-harmonic inverse methodology for the design of RF coils in MRI［J］.IEEE Transactions on Biomedical Engineering，2002，49（1）：64－71.

［12］While PT，Forbes LK，Crozier S.A time-harmonic target-field method fordesigning unshielded RF coilsin MRI［J］.Measurement Science and Technology，2005，16（4）：997－1006.

［13］While PT，Forbes LK，Crozier S.A time-harmonic target-field method for designing shielded RF coils in MRI ［J］.Measurement Science and Technology，2005，16（6）：1381－1393.

［14］Mahony C，Forbes LK，Crozier S，et al.A novel approach to the calculation of RF magnetic and electric fields for NMR coils of arbitrary geometry［J］.Journal of Magnetic Resonance Series B，1995，107（2）：145－151.

［15］Brideson MA，Forbes LK，Crozier S.Determining complicated winding patterns for shim coils using stream functions and the target-field method［J］.Concepts in Magnetic Resonance Part A.2002，14（1）：9－18.

［16］Rostislav AL，Reinhold L.A stream function method for gradient coil design［J］.Concepts in Magnetic Resonance Part B：Magnetic Resonance Engineering，2005，268（1）：67－80.

［17］Delves LM，Mohamed JL.Computational Methods for Integral Equations［M］.Cambridge University Press，1985.

［18］Hoult DI，Deslauriers R.Accurate shim-coil design and magnetfield profiling by a power minimization matrix method［J］.Journal of Magnetic Resonance Series A，1994，108（1）：9－20.

［19］Chronik BA，Rutt BK.Constrained length minimum inductance gradient coil design［J］.Magnetic Resonance in Medicine，1998，39（2）：270－278.

［20］Martens MA.Insertable biplanar gradient coils for magnetic resonance imaging［J］.Review of Scientific Instruments，1991，62（11）：2639－2645.

［21］Jin Jianming.Electromagnetic Analysis and Design in Magnetic Resonance Imaging［M］.New York：CRC，1999：236.

［22］Parisa H，Stephen DH，William BH，et al.Finite-length shim coil design using a Fourier series minimum inductance and minimum power algorithm［J］.Concepts in Magnetic Resonance Part B：Magnetic Resonance Engineering，2010，37B（4）：245－253.