缝合式和机械吻合式搭桥模型的血流动力学数值模拟

高进涛 王国栋 肖聚亮

（天津大学机械工程学院，天津 300072）

引言

冠状动脉搭桥术中，传统手工缝合技术依然是实现移植血管与动脉端-侧吻合的首选方法，该方法不仅对医生的手术技巧要求较高，且在钳夹动脉操作中容易造成动脉内膜斑块脱落，引起血栓和脑卒中等并发症。近年来，机械吻合器作为一种心脏不停跳情况下血管快速端-侧吻合装置，随着微创冠状动脉搭桥手术的发展，逐渐得到大量临床应用。该技术摒弃了传统手工缝合技术中采用的缝合线，能够减少对动脉的钳夹，不仅有效避免了血栓和脑卒中等并发症的发生，而且实现了血管开孔和吻合连接等环节的连续、快速、精准操作［1－3］。由于机械吻合技术仍处于研究与发展阶段，存在吻合区内膜增生的问题，且内膜增生是影响搭桥长期通畅率、导致手术失败的主要原因［4］。血流动力学因素是引起冠脉搭桥手术中内膜增生及其他血管疾病的主要原因，包括回流、二次流、局部高压、较低的壁面切应力、较高的壁面切应力梯度等［5－6］。机械吻合器的引入会引起吻合区几何形状发生变化，而吻合区几何形状的微小差别，可能会极大地影响血管壁面切应力的分布［7］，对血流动力学产生一定的影响，然而对于该模型中血流动力学的分析无人涉及。

以往的研究往往针对于远端吻合（移植血管与冠状动脉间的吻合），因为此处内膜增生往往是导致冠状动脉搭桥术失败的主要原因［8］，对于近端吻合（主动脉与移植血管间的吻合）的研究则相对更少。然而，近端吻合对促进细胞分裂及血小板的活化会产生一定的影响，当处于活跃状态的血小板沿着移植血管流向远端时，在远端吻合区低切应力处聚集，进而会引起远端吻合区内膜增生［9－10］。

本研究运用有限单元数值模拟方法和血流动力学的基本原理，比较了传统缝合模型和机械吻合模型分别在近端吻合区血流动力学因素的分布情况，对机械吻合技术的临床应用具有重要的指导意义。

1 数学物理模型

1.1 几何模型

机械吻合器是一种自身可扩张的装置，其结构如图1（a）所示，中央是一个由相互连接的椭圆拱组成的圆柱空腔，两端各有一套可变形的针脚，完成吻合后如图1（b）所示。根据现行的机械吻合器的特点［1，3，11］，采用机械吻合技术完成冠状动脉搭桥手术后，移植血管与主动脉间的夹角只能为90°。移植血管位于吻合器圆柱空腔内，吻合器内侧针脚穿透外翻的移植血管并紧固于主动脉内壁上，外侧针脚则紧固于主动脉外壁上，通过吻合器自身的张紧力实现移植血管与主动脉的周向密封，吻合区有一小部分凸起。

冠状动脉搭桥术近端吻合一般在人体胸主动脉中进行，吻合位置取在主动脉弓近升主动脉处，模型中主动脉取1°锥角。鉴于主动脉弓的3个分支距离搭桥位置较远，对吻合区的血流动力学影响可以忽略［12］，不考虑主动脉弓分支的影响。所采用的几何模型如图2所示，图2（a）为总体视图，图2（b）为缝合模型A处局部视图（为与仿真结果统一起见，将局部视图旋转一定角度），移植血管在吻合区与主动脉内壁平齐；图2（c）为机械吻合模型A处局部视图，移植血管沿吻合区轴向有0.8 mm的凸起，这是两个模型的唯一区别。在两个几何模型中，升主动脉长度为50 mm，降主动脉长度为150 mm。主动脉弓进口内径为30 mm，主动脉弓顶部内径为27.4 mm，主动脉弓出口内径为25 mm。移植血管与主动脉在主动脉弓处吻合，吻合区轴线与水平方向成10°夹角。移植血管内径为5 mm，移植血管垂直于主动脉直段长度为12 mm（直段长度根据搭桥位置而有所不同）。为获得稳定的边界条件，一段长为30 mm的直管加在移植血管的末端。

1.2 数学模型及流动方程的确立

由于血管壁的实际变形量不大，将血管定义为刚性管。由于血液流动的切变率变化不大，血液黏度可视为不变，进而将血液假设为不可压缩的牛顿黏性流体［13］。血液黏性系数 μ=0.003 5 kg/m/s，密度 ρ=1 050 kg/m3。为判断血流是层流还是湍流，需用到雷诺数，其定义为：Re=ρVD/μ，其中，ρ为流体的密度，V是流体的速度，D为圆管内径，μ为流体的黏度。根据人体安静状态下平均脉搏输出量为70 ml及心率为75次/min，得到Re=1 137＜2 300，因此可判定血流为层流。频率参数α（也称为Womersley数）是作为判断血液流动是否为定常的依据，其定义为：α=，式中，ω =2π/T，T为心动周期，υ=μ/ρ为血液的运动黏性系数，ρ为血液密度。对于胸主动脉内血液流动，α=19.2，因此属于非定常流动。

血液的流动规律需满足以下两组控制方程［14］：

（1）质量守恒方程，其微分形式的连续方程为

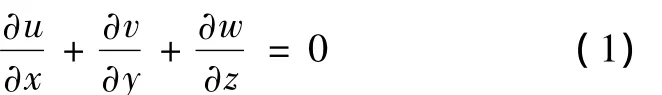
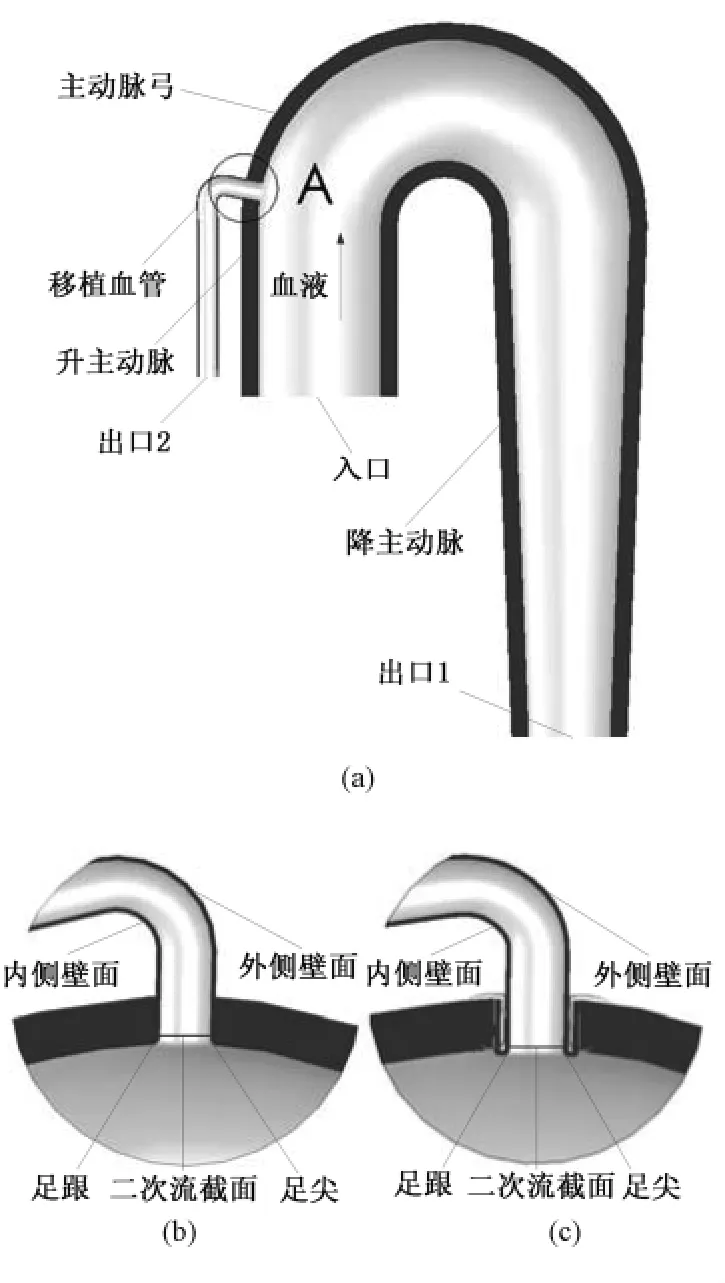
图2 几何模型。（a）总体视图；（b）缝合模型A处局部视图；（c）机械吻合模型A处局部视图Fig.2 The diagram of the geometric models.（a）The general views；（b）A partial views in suturing model；（c）A partial views in sutureless model

（2）动量守恒方程，其微分形式的运动方程为

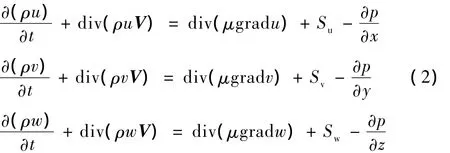
式中，u、v、w 分别是速度矢量 V 在 x、y、z方向的分量，m/s；μ为流体黏度系数，kg/m/s；p为压力，Pa；Su、Sv、Sw分别为动量守恒方程的广义源项，且对于黏性为常数的不可压缩流体，Su=Sv=Sw。

1.3 边界条件的确立

血流动力学问题的求解包括流场速度、压力及壁面切应力等，为得到这些量的流动特性，需要设定合理的边界条件和初始条件。

（1）壁面边界条件：所有壁面认为是刚性的、无滑移的。采取此种假设，是因为相对于因几何形状及边界条件引起的流动特性的变化而言，血管壁的柔顺性引起的变化可以忽略。

（2）出口边界条件：移植血管与主动脉的流量比为0.009 55［15］（移植血管与主动脉处血液的流量分别约为55 mL/min和5 550 mL/min），出口处取自由出流并给定流量比，主动脉出口流量比例取0.99，移植血管出口流量比例取0.01。

（3）进口边界条件：在计算确定进口速度V（t）时，取典型的人体心脏搏动频率为75次/min，因此心脏博动周期为0.8 s。采用如图3所示的主动脉进口速度（V（t），m/s）函数［16］，其表达式为

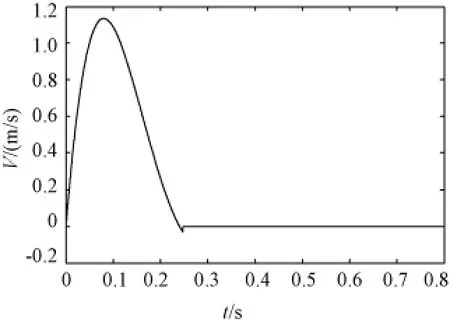
图3 入口速度（一个周期）Fig.3 Velocity at entrance in a cardiac cycle

（4）计算初值条件：所有动力学参量的初值均取零。时间步长为0.01 s。

1.4 求解方法

本研究统一采用Solidworks建模，将建好的模型导入ANSYS-ICEM中进行网格划分，最后利用Fluent6.3软件进行流体分析计算和结果后处理。

（1）计算区域划分为血液流动区、血管壁面、血液进口断面、血液出口断面等区域，分别给定边界条件和计算初始条件，Fluent软件包中附有用户自定义C程序可以用来求解入口处速度模型。

（2）微分方程组离散化格式采用二阶精度的迎风格式；计算中采用变量限制技术，保证计算的收敛性和稳定性。

（3）由于计算区域的不规则性，所以采用非结构化网格进行网格划分，其中采用边界层网格进行加密处理，以获得较为准确的壁面切应力分布。并对划分6好的网格进行质量检查，保证网格的节点压扁程度、单元的偏斜率以及纵横比满足使用要求。网格划分过程中，通过细化网格来检验网格密度对结果（以血流速度分布为例）的影响。结果发现，当缝合模型和机械吻合模型的流动区域分别被划分成559 367和573 238个有限单元时，已能满足计算要求。因为随着网格的加密，如网格数从5.5×105直到1.5×106时，并不会引起血流速度分布发生明显的变化，结果差别不超过0.2％。为提高计算效率，目前的网格密度能给出可信的结果。

经过几个周期的运算，获得了稳定的收敛解。

2 结果和讨论

针对速度场、二次流、压力、壁面切应力等各个流场物理量进行分析，一般而言，吻合区上游和下游的流场分布明显不同，主要关注吻合区附近的流场情况，因为此处更容易引起近端吻合区内膜增生和血小板的活化，进而会引起远端吻合区内膜增生，影响搭桥的长期通畅率。

2.1 吻合区血液流场的速度矢量分布

一个心动周期内不同时刻（t=0.01、0.04、0.08、0.15、0.20、0.24、0.27、0.7 s），缝合模型和机械吻合模型在吻合区的速度矢量分布如图4所示。

经比较发现，两模型在同一时刻的仿真结果具有以下相同之处：由图4（a）可知，当0 s＜t＜0.04 s时，主动脉中血流速度较小，当血流到达吻合区“足跟”处时，血流方向发生偏离，部分血液流入移植血管中。当血流到达吻合区“足尖”处时，血流发生分叉，并于此处形成一个流动驻点，速度较低。由图4（b）、（c）可知，当0.04 s≤t＜0.08 s时，随着血流速度的增大，沿着移植血管的内侧壁面出现回流并形成一个低速区。在t=0.08 s时刻，移植血管中的血流速度达到最大，此时的回流现象比较明显。由图4（d）～（f）可知，当0.08 s＜t≤0.24 s时，移植血管中的血流速度逐渐减小，沿移植血管的轴线方向出现漩涡，随着时间的推移，漩涡中心逐渐逼近主动脉，使得更多的血液从移植血管回流至主动脉。由图4（g）可知，当0.24 s＜t≤0.27 s时，反向流动的血液在移植血管中占主导地位，吻合区入口处血流方向反向，吻合区“足尖”处流动驻点消失。由图4（h）可知，当0.27 s＜t≤0.8 s时，移植血管中的回流和漩涡现象消失，血液以较低的速度从移植血管流回主动脉。由以上的仿真结果可以看出，两个模型均在吻合区“足尖”处形成一个流动驻点，沿移植血管内侧壁面处形成一个低速区，且在心动周期中均出现回流现象，这些位置易引起血小板的活化及内膜增生。

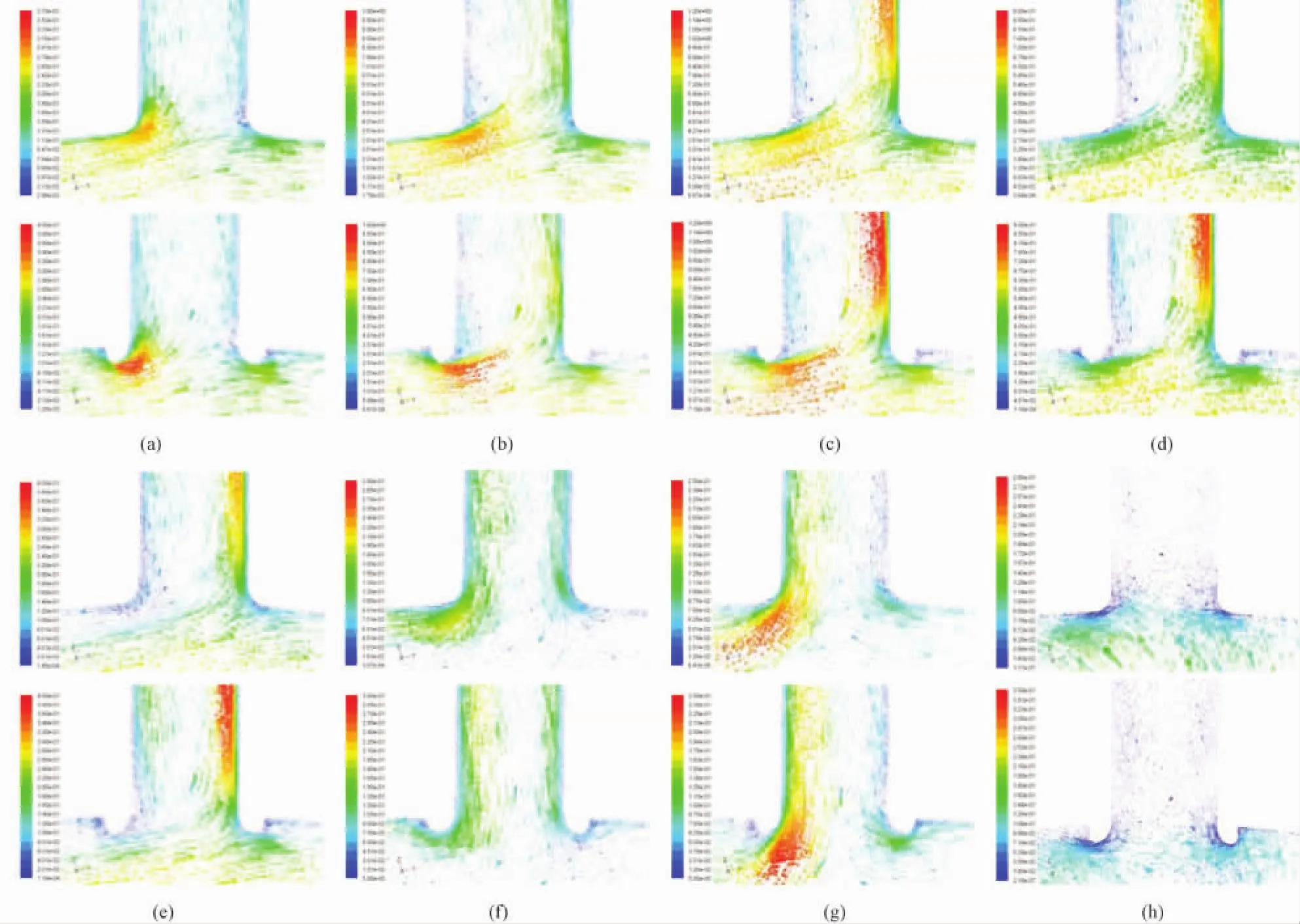
图4 一个心动周期对称面内速度矢量分布（上行为缝合模型，下行为机械吻合模型）。（a）t=0.01 s；（b）t=0.04 s；（c）t=0.08 s；（d）t=0.15 s；（e）t=0.20 s；（f）t=0.24 s；（g）t=0.27 s；（h）t=0.70 sFig.4 Velocity vector in symmetry plane within a cardiac cycle（upper：hand-sewn model；lower：sutureless anastomosis model）.（a）t=0.01 s；（b）t=0.04 s；（c）t=0.08 s；（d）t=0.15 s；（e）t=0.20 s；（f）t=0.24 s；（g）t=0.27 s；（h）t=0.70 s

然而，两模型的仿真结果也略有差异：在缝合模型与机械吻合模型中，移植血管入口处的血流均来自近主动脉外侧壁处，但机械吻合模型由于存在凸起，相对于缝合模型而言，移植血管入口处的血流主要来自于更接近主动脉轴心处的血流，速度相对较大，沿移植血管内侧壁面的低速区范围也相对较大，回流现象明显。回流区是内皮细胞增生的危险区［17］，易引起血小板的活化，当处于活跃状态的血小板流向远端吻合区时，则会引起远端吻合区的内膜增生，从而影响搭桥手术的长期通畅率。此外，流场的分布情况将会影响到壁面切应力的量值和分布，这在后面的壁面切应力分析中将得到证实。

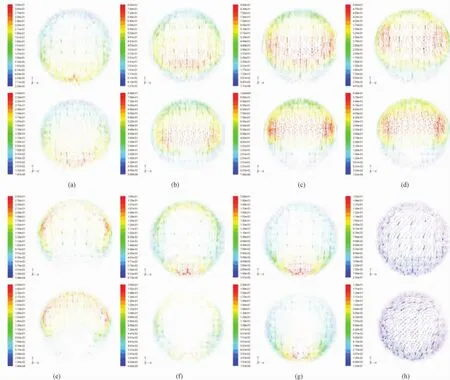
图5 吻合区横截面内二次流分布（上行为缝合模型，下行为机械吻合模型）（a）t=0.01 s；（b）t=0.04 s；（c）t=0.08 s；（d）t=0.15 s；（e）t=0.20 s；（f）t=0.24 s；（g）t=0.27 s；（h）t=0.70 sFig.5 Second flow at anastomosis cross section within a cardiac cycle（upper-hand-sewn model；lower-sutureless anastomosis model）.（a）t=0.01 s；（b）t=0.04 s；（c）t=0.08 s；（d）t=0.15 s；（e）t=0.20 s；（f）t=0.24 s；（g）t=0.27 s；（h）t=0.70 s

2.2 吻合区横截面内二次流分布

一个心动周期内不同时刻（t=0.01、0.04、0.08、0.15、0.20、0.24、0.27、0.70 s），缝合模型和机械吻合模型在吻合区横截面内的二次流分布如图5所示，所取横截面如图2中（b）和（c）所示，与移植血管血流入口截面的轴向距离为1 mm。

由图5可知，在心动周期内，血液在移植血管吻合区中呈现明显的二次流动，且在收缩减速期二次流发展较快，随着速度的减小，二次流不断加剧，并于收缩末期达到最大；在舒张期，随着轴向血流速度的减小，二次流逐渐减弱。二次流的涡心自近壁面处沿水平方向略有波动，垂直方向变化不太明显。二次流的存在导致流体介质的流线呈螺旋形并延长了介质驻留时间，增加了血液同移植血管表面的接触机会，易造成血小板的活化，引起远端吻合区内膜增生，影响冠状动脉搭桥术的长期通畅率。比较两个模型的仿真结果发现，相对于缝合模型而言，机械吻合模型二次流的径向速度较大，意味着二次流强度较大，且涡流的涡心距离壁面较近，会增加血液同易形成血栓的移植血管壁的接触机会，进而会促进血小板的活化，引起远端吻合区的内膜增生［9］。

2.3 吻合区压力分布

一个心动周期内不同时刻（t=0.01、0.04、0.08、0.15、0.20、0.24、0.27、0.7 s），缝合模型和机械吻合模型在吻合区的压力分布如图6所示。

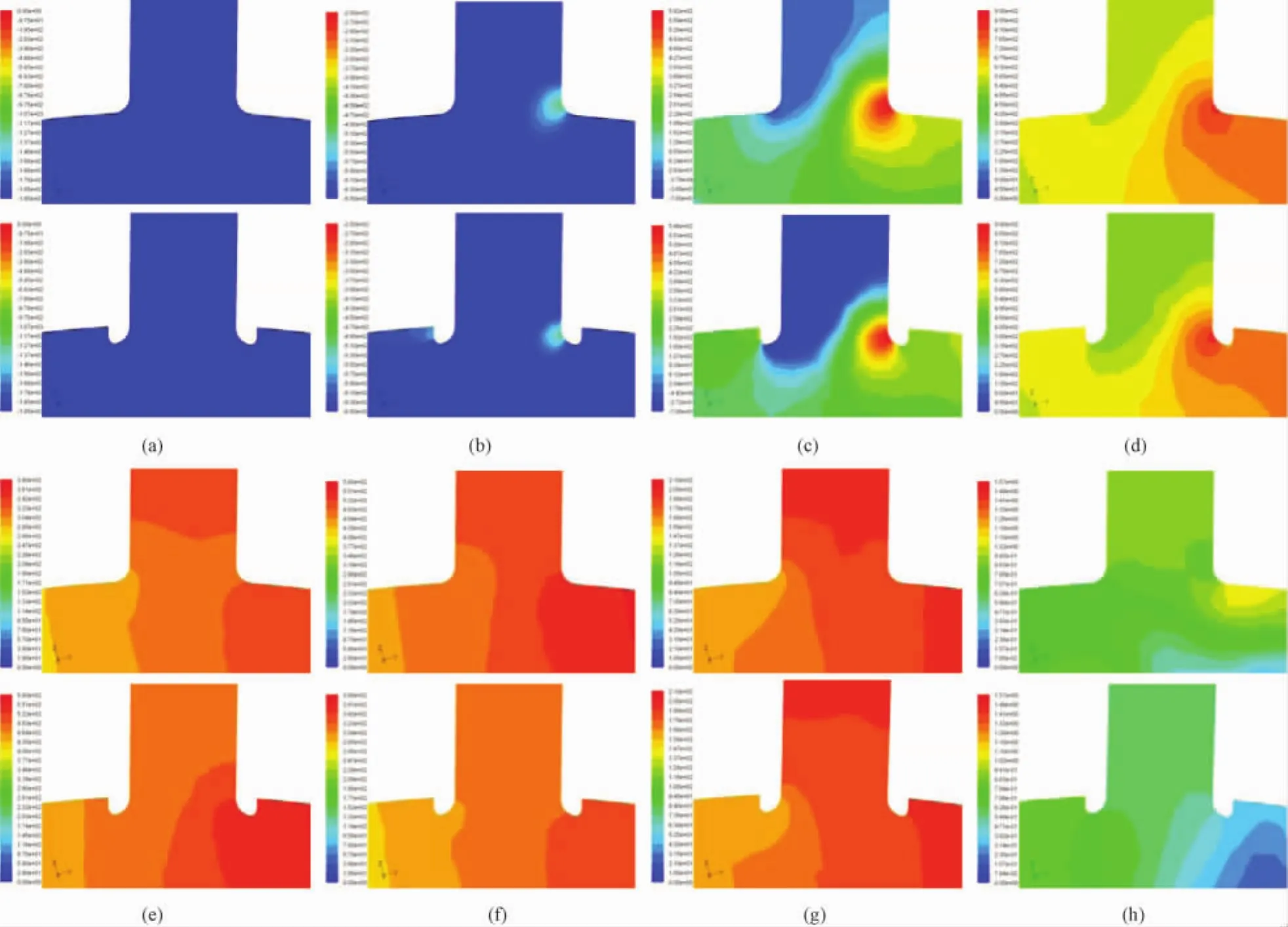
图6 一个心动周期对称面内压力分布（上行为缝合模型，下行为凸起模型）（a）t=0.01 s；（b）t=0.04 s；（c）t=0.08 s；（d）t=0.15 s；（e）t=0.20 s；（f）t=0.24 s；（g）t=0.27 s；（h）t=0.70 sFig.6 Pressure distribution in symmetry plane within a cardiac cycle（upper：hand-sewn model；lower；sutureless anastomosis model）.（a）t=0.01 s；（b）t=0.04 s；（c）t=0.08 s；（d）t=0.15 s；（e）t=0.20 s；（f）t=0.24 s；（g）t=0.27 s；（h）t=0.70 s

经比较发现，两模型在相同时刻的仿真结果具有以下相同之处：由图6中（a）～（c）可知，当0 s＜t＜0.08 s时，吻合区“足尖”处的压力随着血流速度的增大而升高，在t=0.08 s时刻，血流速度达到最大，吻合区“足尖”处的压力也达到最高，吻合区“足跟”处的压力则相对较低。由图6中（d）～（g）可知，当0.08 s＜t≤0.27 s时，吻合区“足尖”处的压力逐渐降低，吻合区“足跟”处的压力则逐渐升高，最终二者的压力基本相同。由图6（h）可知，当0.27 s＜t≤0.8 s时，吻合区的压力分布比较均匀，“足尖”与“足跟”处的压力相差不大。仿真结果显示，缝合模型吻合区的压力相对较高，其吻合区“足尖”处的高压范围相对较大，但分布比较均匀，变化梯度较小；与之相反，机械吻合模型吻合区“足尖”处高压范围则相对较小，却具有较大的变化梯度。一般认为吻合区“足尖”处呈现较低压力对改善吻合区的血流动力学因素是有益的，但仿真结果显示，两个模型均在吻合区“足尖”处出现局部高压，高的血压会显著增强血小板活化能力，进而导致血栓的形成，并引发其他严重的血栓性疾病［18］。

2.4 吻合区壁面切应力分布

一个心动周期内不同时刻（t=0.01、0.04、0.08、0.15、0.20、0.24、0.27、0.7 s），吻合区血管壁面切应力分布如图7所示。仿真结果显示，壁面切应力随吻合区入口速度梯度的增减而增减。

经比较发现，两模型在同一时刻的仿真结果具有以下相同之处：由图7中（a）～（c）可知，当0 s＜t＜0.08 s时，由于吻合区入口处几何形状引起速度发生突变，越接近吻合区“足跟”处，壁面切应力越大，而沿移植血管内侧壁面低速区的壁面切应力则相对较小；吻合区“足尖”流动驻点处的血流速度梯度较小，对应的壁面切应力也较小，越过流动驻点处，沿移植血管外侧壁面的壁面切应力逐渐增大，直至达到充分发展状态而保持不变。在t=0.08 s时刻，随着移植血管中血流量达到最大，壁面切应力也达到最大。由图7中（d）～（g）可知，当0.08 s＜t≤0.27 s时，受到回流的影响，移植血管中的血液沿内侧壁面反向流回主动脉，内侧壁面低速区的血流速度和速度梯度逐渐增大，壁面切应力也随之增大，并于吻合区“足跟”处达到最大；与此同时，吻合区“足尖”处血流方向也发生变化，流动驻点消失，移植血管外侧壁面血流速度和速度梯度逐渐减小，壁面切应力也随之减小。由图7（h）可知，当0.27 s＜t≤0.8 s时，随着血流速度和速度梯度的减小，内侧壁面与外侧壁面的切应力均随之减小，总体变化幅度较小。由图7可知，两个模型的低壁面切应力主要出现于吻合区“足尖”的流动驻点处以及移植血管的内侧壁面处，正好与该处的低速区相对应。

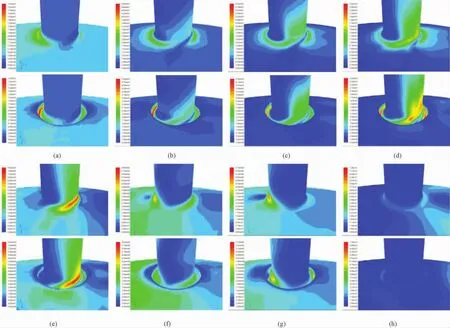
图7 一个心动周期壁面切应力分布（上行为缝合模型，下行为凸起模型）。（a）t=0.01 s；（b）t=0.04 s；（c）t=0.08 s；（d）t=0.15 s；（e）t=0.20 s；（f）t=0.24 s；（g）t=0.27 s；（h）t=0.70 sFig.7 Wall shear stress distribution within a cardiac cycle（upper：hand-sewn model；lower：sutureless anastomosis model）.（a）t=0.01 s；（b）t=0.04 s；（c）t=0.08 s；（d）t=0.15 s；（e）t=0.20 s；（f）t=0.24 s；（g）t=0.27 s；（h）t=0.70 s

然而，两模型的仿真结果也存在一些差异：首先，相对于缝合模型而言，机械吻合模型吻合区存在凸起，入口处血流速度和速度梯度较大，吻合区“足跟”处壁面切应力相对较大，由图7可知，缝合模型沿吻合区的壁面切应力值在0～30 Pa之间变化，机械吻合模型沿吻合区的壁面切应力值在0～50 Pa之间变化。机械吻合模型吻合区附近的壁面切应力相对较大，较大的壁面切应力对减缓内膜增生是有益的。然而，相对于缝合模型而言，机械吻合模型在吻合区“足跟”处出现较高的应力集中现象，主要是由于血管沿吻合区几何形状发生剧烈变化引起的，异常高的应力集中则对血管壁重构极其有害，并可能导致内皮细胞的损伤和再狭窄的形成及发展［19］。并且沿机械吻合模型吻合区的轴向和周向，壁面切应力均具有更大的空间变化梯度，高壁面切应力梯度更容易引起血小板的活化和内膜增生，尤其是在吻合区“足跟”处，这些区域是引起血管病变、影响搭桥长期通畅率的危险区。然而，在真实的“在体”手术中，血管壁会发生顺应性变形，吻合区的边界几何形状不会如此“尖锐”，吻合区的壁面切应力也不会像仿真结果那样变化剧烈，壁面切应力梯度也要小得多。相对于缝合模型而言，机械吻合模型由于存在凸起，沿移植血管内侧壁面的低速区范围较大，其对应的低壁面切应力范围也相对较大，而较低的壁面切应力对血小板的活化和聚集具有重要的影响，低壁面切应力会减少一种血小板聚集抑制剂的分泌，而这种抑制剂在调节局部血流和防止内膜增生形成机制中起重要作用［20］。

3 结论

为了说明机械吻合器的引入，对冠状动脉搭桥术近端吻合区血流动力学因素的影响，利用计算研究方法对传统缝合搭桥和机械吻合搭桥模型中的血流动力学进行了研究和比较分析。结果发现，相对于传统缝合模型而言，机械吻合模型在吻合区入口处具有较大的血流速度、明显的应力集中现象、较强的二次流、较大的壁面切应力梯度，沿移植血管内侧壁面的低速区和低壁面切应力区范围相对较大。这些因素在一定程度上容易引起近端吻合区内膜增生和血小板的活化，当处于活跃状态的血小板在远端吻合区聚集时，容易引起远端吻合区的内膜增生。因此，有必要对机械吻合器进行优化设计，改善吻合区的几何形状，尽量避免产生凸起，保证主动脉流来的血液能顺畅地流入移植血管中，减缓近端吻合区的内膜增生和血小板的活化，进而减缓远端吻合区内膜增生，提高冠状动脉搭桥术的长期通畅率。

［1］Riess FC，Helmold H，Hilfer I，et al.Clinical experience with the CorLink device for proximal anastomosis of the saphenous vein to the aorta：A clinical，prospective，and randomized study［J］.The Heart Surgery Forum，2002，5（4）：345 －353.

［2］Sun Anqiang，Fan Yubo，Deng Xiaoyan，et al.Hemodynamic performance ofa sutureless anastomosis device（the Graft Connector）：a numerical study［J］.Int J Artif Organs，2010，33（6）：392－398.

［3］Dohmen G，Hatama N，Goetzenich A，et al.PAS-Port clampless proximalanastomotic device forcoronary bypass surgery in porcelain aorta［J］.European Journal of Cardio-thoracic Surgery，2011，39（1）：49 －52.

［4］Gummert JF，Opfermann U，Jacobs S，et al.Anastomotic devices for coronary artery bypass grafting：Technological options and potential pitfalls［J］.Computers in Biology and edicine，2007，37（10）：1384－1393.

［5］Zhang JM，Chua LP，Ghista DN，et al.Numerical investigation and identification of susceptible sites of atherosclerotic lesion formation in a complete coronary artery bypass model［J］.Med Biol Eng Comput，2008，46（7）：689 －699.

［6］乔爱科，刘友军.股动脉双路搭桥的血流动力学仿真［J］.中国生物医学工程学报，2006，25（2）：211 －218.

［7］Milner JS，Moore JA，Rutt BK，et al.Hemodynamic of human carotid artery bifurcations：computational study with models reconstructured from magnetic resonance imagining of normal subjects［J］.Journal of Vascular Surgery，1998，28（1）：143 －156.

［8］Shaik E，Hoffmann KA，Dietiker JF.Numerical simulations of pulsatile Non-Newtonian flow in an end-to-side anastomosis model［J］.Simulation Modeling Practice and Theory，2008，16（9）：1123 －1135.

［9］Chua LP，Zhang JM，Yu SC，et al.Numerical study on the pulsatile flow characteristics of proximal anastomotic model［J］.Proc Inst Mech Eng，2005，219（5）：361 －379.

［10］Chua LP，Ji Wenfa，Zhou Tongming.In vitro study on the steady flow characteristics of proximal anastomotic models［J］.International Communications in Heat and Mass Transfer，2005，32（3－4）：464－472.

［11］Redaelli A，Maisano F，Ligorio G，et al.Flow dynamics of the St Jude Medical Symmetry aortic connector vein graft anastomosis do not contribute to the risk of acute thrombosis［J］.Journal of Thoracic and Cardiovascular Surgery，2004，128（1）：117－123.

［12］杨俊勇.心血管系统（主动脉弓）血液流场计算［D］.杭州：浙江理工大学，2008.

［13］林亚华，景在平，赵志清，等.人胸主动脉血液脉动流的三维数值分析［J］.第二军医大学学报，2006，27（8）：867 －875.

［14］李言芝.B型主动脉夹层血液流动数值模拟分析［D］.兰州：兰州理工大学，2011.

［15］Chua LP，Zhang JM，Zhou TM.Numerical study of a complete anastomosis model for the coronary artery bypass［J］.Heat and Mass Tranf，2005，32（3）：473 －482.

［16］邱霖，岑人经.有锥度角的主动脉弓血液脉动流数值分析［J］.医用生物力学，2004，19（2）：74 －78.

［17］刘有军，乔爱科，黄伟.冠状动脉移植管的血流动力学数值模拟［J］.中国生物医学工程学报，2004，23（4）：370 －377.

［18］叶显华，徐鹏，王宁夫，等.高血压对冠心病血小板活化作用的影响［J］.心脑血管病防治，2011，11（1）：27 －28.

［19］乔爱科，刘有军，李晓阳.股动脉对称搭桥术的数值分析［J］.北京工业大学学报，2006，32（4）：363 －36.

［20］姜宗来.生物力学：我国生物力学研究现状与展望［J］.中国生物医学工程学报，2011，30（2）：161－168.