基于小波包变换的特征提取方法分析fMRI数据

支联合 谭素敏 杨建国

1（周口师范学院物理与电子工程系，周口 466001）

2（周口师范学院附属医院，周口 466001）

3（哈尔滨工业大学威海校区汽车工程学院，威海 264209）

引言

由于具有无创、可重复和时空分辨率高等特点，功能磁共振成像技术（functional magnetic resonance imaging，fMRI）在人脑解剖定位、功能成像和网络连接研究中起着日益关键的作用［1－2］。但是，fMRI数据里除包含激活信号外，还混杂有高频噪声、低频漂移等干扰。因此，设计灵敏度高、特异度好的fMRI数据处理方法成为重要的研究课题。其中，灵敏度是识别激活体素的能力，取决于去除干扰能力的强弱；特异度是区分激活体素和非激活体素的能力，决定于去除干扰时对激活信号的保护程度。

统计参数图（statistical parametric mapping，SPM）是目前国际权威的fMRI分析方法［3］，用试验刺激函数与血流动力学函数卷积模拟试验刺激诱导的激活信号，用高通滤波去除低频漂移，再基于广义线性模型对体素数据进行分析，最新版本为SPM8。具有多尺度分析功能的小波变换也广泛应用于fMRI数据在内的医学信号处理［4－6］。比如，基于小波去噪理论［7］去除fMRI数据的高频噪声［8］，基于多尺度分析特性去除fMRI数据的低频漂移［9］，在小波域对fMRI数据进行广义线性模型建模［10］等。

与上述方法仅去除单一高频或低频干扰不同，多尺度特征提取（multiscale feature extraction，MFE）基于离散小波变换（discrete wavelet transform，DWT）分割fMRI数据的频谱，进而通过重构激活信号存在的子带同时去除高频和低频干扰［11］，显著提高了后续统计检测性能。理论上，小波包变换（wavelet packet transform，WPT）比小波变换对频带的分割更精细，因此更适合MFE提取激活信号和去除干扰。为此，基于WPT构建新MFE，并设计矩阵算法代替逐体素迭代算法快速提取激活信号，同时与原有MFE和SPM8进行比较。

1 材料和方法

1.1 听觉fMRI试验

一个被试的听觉fMRI试验数据下载于SPM网站（www.fil.ion.ucl.ac.uk/spm），并被许可使用。试验为组块型设计，任务组块刺激是给被试听双音节单词，语速为60个/min。试验以静息组块开始，任务与静息两种组块交替进行，每个组块持续42 s。用2 Tesla Siemens扫描机以f0=1/7Hz的抽样频率获取一个被试共96帧全脑BOLD/EPI图像。每帧图像大小为64体素×64体素×64体素，体素大小为3 mm×3 mm×3 mm。前12帧图像因磁场稳定性原因舍弃不用，剩余84帧图像则进行SPM8方法常规预处理，包括被试运动矫正、标准化到 M NI解剖空间、空间高斯平滑及去除脑外体素。

试验刺激的周期为 T =84 s，时宽为42 s，因此激活信号的频率组分除直流外，还应包括基频1/T=0.011 9Hz和三倍频 3 /T=0.035 7Hz、五倍频5/T=0.059 5Hz等。图1（a）显示了SPM8模拟的激活信号X的频谱。

1.2 方法

1.2.1 小波包变换

WPT基于DWT发展而来，包括分解和重构两个互逆的运算，为易于理解先叙述DWT的原理。对于确定的小波低通滤波器L、高通滤波器H和下采样算子D0，一个体素时间序列数据y经J级DWT分解后变换为分布在J+1个时频尺度里的小波系数集合cy=［aJ，dJ，dJ－1，…，d1］

式中，分解深度j=1，2，…，J；aj和dj分别为第j级低频尺度和高频尺度。与DWT分解只分割低频尺度不同，WPT对高频尺度和低频尺度同时进行分割

式中，分解深度j=1，2，…，J；在任一深度j，i=1，2，…，I－1，I， 其中 I =2j－1；sij－1表示第j－1层的第i个小波包尺度。上述分解都称为多尺度分析，把体素频带分割成了一系列时频特性各异的尺度（子带）。对于理想小波滤波器，aJ的频带为［0，f0/2J+1），dj的为（f0/2j+1，f0/2j］，WPT的 2J个尺度则平均分割体素频带［0，f0/2］。可见，分解同样的深度时WPT对频带的分割更为精细，这是选用WPT代替DWT构建新MFE的原因。但因为分割精细，WPT耗时因此更多。

重构是分解的逆过程，DWT的重构为

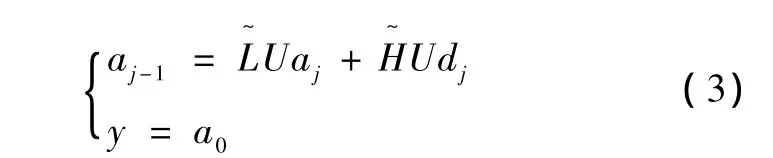
式中，U为隔点插零算子，和分别为小波低通和高通重构滤波器，这时的j=J，J－1，…，1。而WPT则为

上述是对全部尺度的重构，如果重构时保留特定尺度里的系数不变，而将剩余尺度里的系数全部置零则称为特征尺度重构。这种重构虽则多了系数置零的步骤，但能够有选择地从y中提取感兴趣的子带成分。

1.2.2 多尺度特征提取fMRI数据

WPT更精细的频带分割能力为利用特征尺度重构提取fMRI数据里的激活信号提供了更好的技术支持，新MFE包括3个步骤。

步骤1：识别特征尺度。激活信号存在的尺度为特征尺度，其它尺度为干扰尺度。取J=4用WPT把模拟的激活信号X分解在16个尺度里，并逐尺度地进行重构。对比每个重构尺度的频谱与X的频谱，发现X的成分主要分布在除、和外的尺度里。这样，就把上述3个尺度及确定为干扰尺度，剩余的12个为特征尺度。尽管尺度包含X的直流成分，但体素数据的这一尺度里也包含低频漂移，故也视为干扰尺度。对X进行特征尺度重构，得到的信号为E1X，其频谱显示在图1（b）里。

步骤2：提取 y 里包含的激活信号。也即对 y进行特征尺度重构，得到的信号为E1y。

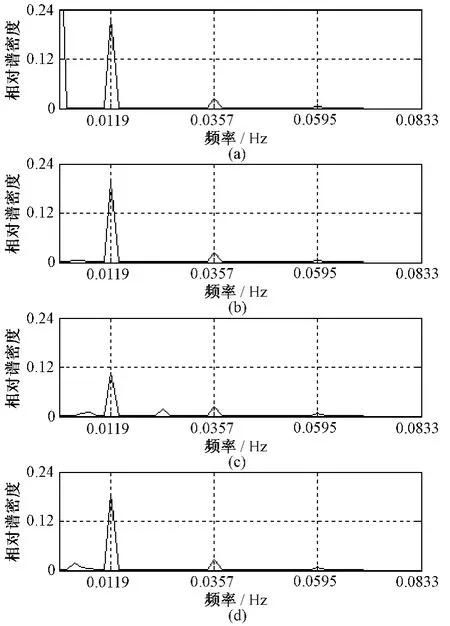
图1 3种方法分析听觉数据涉及到的频谱。（a）SPM8；（b）E1X；（c）尺度d31；（d）E2XFig.1 The frequency spectrums used by three methods for the auditory data.（a）SPM8；（b）E1X；（c）the scale d31；（d）E2X

fMRI数据里体素具有海量性质，WPT速度又慢，因此常规基于迭代算法的一个体素接着一个体素地进行特征尺度重构非常耗时。为此，设计基于WPT的矩阵算法一次性地对诸多体素进行特征尺度重构式中，Y是由体素数据作为每一列组成的数据矩阵，特征提取矩阵M则通过对N阶单位方阵的每一列都进行特征尺度重构得到，N为体素数据长度，在本研究为84；eY为提取的激活信号矩阵，每一列对应一个体素。

步骤3：检测激活体素。对E1X和eY里的每一列数据进行相关分析，并将相关系数r用Fisher'sZ变换转化为Z值

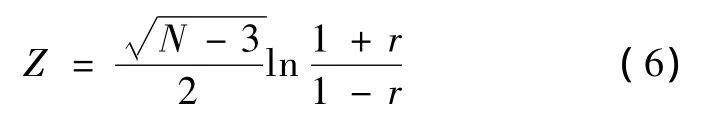
对于基于DWT的MFE方法，第一步也是识别特征尺度。同样取J=4，分析频谱发现X的成分主要分布在尺度d31（即d3和d1的组合）里，但重构这两个尺度得到的频谱显示了严重的混频，即出现了X没有的频率成分，见图1（c）。这是把尺度 a4和d42里的系数设置为零的缘故。为避免混频，取J=5且只把a5视为干扰尺度，而把d54321视为特征尺度，得到的重构信号记为E2X，其频谱显示在图1（d）里。确定特征尺度之后，剩余的两个步骤与WPT的相同。两种方法的程序编写都基于Matlab7.2小波工具箱，小波都用sym2。

对于SPM8，采用其网站提供的方法进行分析，用到的高通滤波的截止频率为其缺省的1/128Hz，基于广义线性模型用t-检验逐体素地检验任务与静息两状态的差异，最后的t-值通过该软件自带的程序转化为Z值。

选取一定的显著性水平作为阈值，对3种方法得到的Z值进行阈值化。因多重统计检验的原因，作为阈值的显著性水平都基于高斯随机场理论进行修正，修正由SPM8完成。与听觉有关的轴向坐标z=6 mm、10 mm和14 mm脑层上的激活体素按放射学约定的方式显示在MNI解剖图上。

2 结果

图2显示了基于WPT的新MFE、原有的基于DWT的MFE和SPM8分析听觉fMRI试验数据3层脑区的激活Z-图，图中最上面3行选取的阈值为显著性水平P=0.001，最下面一行P=0.05，它们都经过修正。可以看出，尽管3种方法的分析机理不同，但检测到的激活区的位置都相同，并且都在公认的听觉区，因此3种方法的特异度相同，分析结果是可靠的。但同时新MFE检测到的激活区最大，原有MFE的次之，SPM8的最小。因此，新MFE的分析结果在3种方法中是最好的。

表1更详细地提供了这3种方法检测图2中3层脑数据区得到的激活体素个数。与图2一样，表1基于WPT和DWT的MFE的阈值都选为修正的P=0.001，SPM8的为修正的P=0.05。显然，对于每层数据而言，基于WPT的新MFE检测出的激活体素个数都是最多的。进一步计算可知，基于WPT的新MFE检测的激活体素个数比原有MFE多13.2％，比SPM8多30.8％。

因此，综合上述分析结果可知，基于WPT的MFE的分析性能在3种方法中是最优的。

表1 3种方法分析听觉数据检测的激活体素个数Tab.1 Numbers of active pixels detected by three methods for auditory data

图2 3种方法分析听觉fMRI试验一个被试3层数据的激活Z-图（图中显著性水平分别为P=0.001（上三行）和P=0.05（最下一行），这些值都经过高斯随机场理论修正）Fig.2 Theactive Z-mapsgenerated bythethree methods for the auditory fMRI data of a subject（The significant level are P=0.001（the first three rows）and P=0.05（the bottom row）respectively，which are corrected based on Gaussian random field）

3 讨论

WPT显著提高MFE分析性能的根本原因，在于WPT的时频尺度在多尺度分析方法中是最窄的。MFE分析体素信号的根本是借助时频特性各异的尺度把信号频带分割成一系列的子带，在重构时舍弃干扰尺度对应的子带和保留特征尺度对应的子带。显然，如要获得较高的灵敏度，特征尺度里必须包含较少的干扰成分，否则重构时这些干扰无法去除；同样，为了获得较高的特异度，干扰尺度也应该包含较少的激活信号成分，因为这些成分将在重构时舍弃。但在fMRI数据的频谱里，激活信号的频率组分不是全部都集中在一个区段里，而是离散地分布于各干扰成分之间。这样，为了达到上述目的，MFE采用的时频尺度的频宽必须尽可能地窄，以便在精确捕捉激活信号频率组分的同时包含较少的干扰成分。目前常用的多尺度分析方法，除了本文涉及到的WPT和 D WT，还包括提升小波变换和平稳小波变换，但尺度最窄的是 W PT。因此，WPT赋予MFE更好的分析性能。

例如，原有MFE方法基于DWT取J=5把体素频带分割为6个尺度，其中d1的频带范围为［f0/4，f0/2］，涵盖体素频谱的一半，里面虽有激活信号的五倍频成分，但同时包含大量的高频噪声。这样，如把d1选为干扰尺度，则会丢失激活信号，从而损害特异度；如选为特征尺度，则无法去除高频噪声，因此损害灵敏度。所以，对于原有 M FE来说，无论是把d1确定为特征尺度还是干扰尺度都不是最优选择。相反，新MFE基于WPT取J=4时，就已把上述频带范围又细分割成了从一直到共8个尺度，而且尺度、和里没有激活信号成分。于是，通过把这3个尺度选为干扰尺度新MFE就获得了比原有MFE和SPM8更高的灵敏度。而且，由于这样做没有损害激活信号的五倍频成分，所以新MFE又同时维持了与另外两种方法一样的特异度。

除了分析性能方面的考虑外，消耗时间少的方法显然更容易为使用者接受。由于WPT比DWT分割出的尺度多，因此运算时间相对要多，这对于分析海量性质的fMRI数据来说是个缺点。对于本文的听觉数据，在同样配置的计算机条件下，基于WPT和DWT矩阵算法的MFE所用时间都为31 s。SPM8分析fMRI数据的机理与MFE不同，但消耗在超参数估计、参数估计和平滑估计上的时间也为77 s。相反，采用逐体素的方法反复迭代WPT分解、干扰尺度系数置零以及WPT重构这3个步骤，总共消耗了2 918 s，约合48.5 min，在实际中这显然是不能接受的。因此，本文给出的矩阵算法保证了新MFE方法在实际应用中分析海量数据的可行性。

和DWT一样，WPT对小波的选取比较敏感，不同的小波可能给出不同的结果。比如，混频是基于DWT和WPT的特征提取方法的一个共性问题，源于小波滤波器的非理想特性、下抽样不满足抽样定理等，就与小波的选取有关［12］。文献［12］研究发现，小波滤波器的系数越多，混频现象就越不明显。所以，对于一个具体的实际数据而言，合适小波的选取涉及到分析性能、时间消耗和使用者对小波知识的了解等诸多因素，需要综合考量，因此是一个复杂的问题。在多尺度分析中，只有平稳小波变换对小波的选取不太敏感，采用这一变换可以免去小波选取的环节，但这一变换方法与DWT一样对频谱的分割没有WPT精细。所以，未来的研究方向是设计一种既是平稳的又是小波包的多尺度分析方法，即平稳小波包变换，据此获得一种既能精细分割频谱又对小波的选取不太灵敏的fMRI数据分析方法。

4 结论

总之，在目前的多尺度分析技术范围内，WPT赋予MFE更好的灵敏度和特异度来分析fMRI数据，本研究引入的WPT矩阵算法较逐体素的反复迭代算法显著提高了MFE的运算速度，所提出的是一种更为实用的fMRI数据分析方法。

［1］尧德中，罗程，雷旭，等.脑成像与脑连接［J］.中国生物医学工程学报，2011，30（1）：6－10.

［2］包尚联.脑功能成像物理学［M］.郑州：郑州大学出版社，2006：200－207.

［3］Friston KJ，HolmesAP，Worsley KJ，etal. Statistical parametric maps in functional imaging：a general linear approach［J］.Hum Brain Mapping，1995，2（4）：189 －210.

［4］Bullmore E，Fadili J，Maxim V，et al.Wavelets and functional magnetic resonance imaging ofthe human brain ［J］.NeuroImage，2004，23（1）：S234－S249.

［5］ 代 煜，张建勋，雪原.基于小波变换的脊柱振动特征分析［J］.中国生物医学工程学报，2012，31（3）：461－465.

［6］ 王 永轩，邱天爽，刘蓉.基于小波分析方法的脑电诱发电位单导少次提取［J］.中国生物医学工程学报，2011，30（1）：34－39.

［7］ D onoho DL，Johnstone IM.Adapting to unknown smoothness via wavelet shrinkage ［J］.J Am Stat Assoc，1995，90（432）：1200－1224.

［8］ W ink AM，Roerdink JBTM.Denoising functional MR images：a comparison of wavelet denoising and Gaussian smoothing ［J］.IEEE Trans Med Imaging，2004，23（3）：374－387.

［9］ M eyerFG. W avelet-based estimation ofa semiparametric generalized linear model of fMRI time-series［J］.IEEE Trans Med Imaging，2003，22（3）：315－322.

［10］ V an De Ville D，Seghier ML，Lazeyras F，et al.WSPM：wavelet-based statistical parametric mapping ［ J］.NeuroImage，2007，37（4）：1205－1217.

［11］ 支 联合，李玉晓，赵书俊，等.基于离散小波变换的 f MRI数据特征提取［J］.中国医学影像技术，2010，26（6）：1151－1154.

［12］ 杨 建国.小波分析及其工程应用［M］.北京：机械工业出版社，2005：107－128.