基于ARMA模型的心电聚类算法
毛 雪 岷 张 婷 婷 蔡 传 晰 李 琼
(合肥工业大学管理学院,合肥 2 30009)
引言
心电信号(ECG)是从人体表面记录心肌细胞电活动的情况,它携带了很多反映心脏工作状况的信息。在实践过程中,医生从正常的ECG信号中找出心律失常信号是诊断心脏病变的常规检测手段之一[1]。随着数据库知识发现和模式识别等计算机技术的发展[2],心电图的诊断逐渐从人工识别转变为计算机自动识别,至今已有多种算法用于心电图自动分类[3]。通过聚类法从ECG信号中找出心律失常的方法运用广泛,但是直接在原始的ECG序列上进行聚类不仅难度大,而且还会影响算法的准确性和可靠性[4]。利用相应的方法对ECG信号序列进行特征提取,把ECG信号变换到低维空间,这样更有利于提高聚类结果的准确性。
最常用的是根据ECG的波形进行特征提取,心电信号的QRS宽度和RR周期是描述心拍的两个最基本的特征量,彭良瑞等[5]在单片机实时系统上利用QRS波宽度,结合RR间期的参数变化检测室性心律失常;Trahanias等[6]选取了代表ECG波形的四类基元(正向负向波峰、直线段和曲线段),并定义了相关属性字符串,采用串文法来描述心电波形。但是这种方法大都仅针对一个心电周期内重要特征波段而言的,不能反映病症的综合特征和全貌,提取的特征因此受到限制[7]。许多学者也尝试着把一些方法运用到心电信号的特征提取中,如:隐马尔科夫模型[8]、傅里叶变换法[9]、神经网络[10]、小波变换[11],这些算法都有着计算复杂度高、实现困难的问题。同时,隐马尔可夫模型以及神经网络模型的泛化能力还需要大量临床数据的进一步验证,目前,仍处于理论研究阶段[4]。
本研究利用一种较简单的特征提取方法,即若时间序列符合一定的分布特征,则可以用ARMA模型拟合,利用拟合的参数估计为特征,以它们的欧氏距离为结构不相似测度进行聚类。但是直接利用这些系数聚类不符合实际的要求,需要对每维特征加以一定的权重。本文提出以每维特征在首次聚类中的贡献率作为权重,与原来相应的系数相乘得到一个新的系数向量,然后以新系数向量的欧氏距离作为结构不相似测度再聚类。利用此方法对心电信号(ECG)聚类诊断心律失常,得到良好的聚类结果,对实践有一定的指导意义。
1 方法介绍
1.1 基于ARMA模型的聚类方法
1.1.1 ARMA模型介绍
对于平稳时间序列的建模,研究人员提出了“参数化”模型,该模型是根据时间序列的观测值{Xt,t=0,±1,… } 构造一个带有参数的数学模型,使这种“参数化”模型能反映产生时间序列Xt的动态系统的规律性,为预报、控制特征提取提供依据。一般来说,一个变量的现在取值,不仅受其本身过去值的影响,而且也受现在和过去各种随机因素冲击的影响。因此,可建立其数据生成模型为:
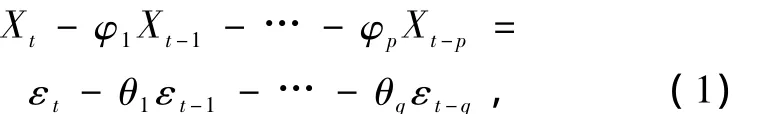
式中,φj(1≤j≤p)和?θj(1≤j≤q)为实数,εt为白噪声过程,即 εt~WN(0,σ2)。式(1)称为p阶自回归q阶移动平均模型,记为 A RMA(p,q)模型。当q=0时,式(1)称为p阶自回归模型,记为AR(p)模型,当p=0,q阶移动平均模型记为MA(q)模型。
1.1.2 相似度定义
每个时间序列经过ARMA模型的拟合之后,会得到一组系数向量数据,利用系数向量之间的欧氏距离来表示时间序列之间的相似度。作如下定义:
定义1 令Xt和Yt均服从零均值ARMA(?p,q)模型,它们的系数向量分别为πX和πY,则其系数向量构成的欧式距离为d可作为两个ARMA模型Xt和Yt之间的结构不相似测度。距离d是一种很好的定义测度,满足距离空间的性质。如果系数向量的维数不同,可采用动态时间弯曲距离定义两个ARMA模型的距离测度。
对时间序列Xt和Yt通过模型识别后,可用ARMA模型进行拟合。假设拟合模型的参数向量分别为πX和πY,由上述方法可定义两个时间序列的距离测度,进而可采用 K 均值和模糊C均值、密度聚类法、最长距离聚类法、最短距离聚类法、最大似然聚类法等方法对时间序列数据进行聚类分析。
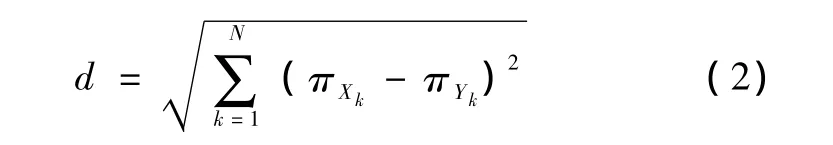
1.2 改进的基于ARMA模型的聚类方法
在运用以上方法进行聚类的过程中,直接利用拟合ARMA模型系数的欧氏距离作为相似度测度,就会存在一个问题:每个系数在距离测度中的贡献率是相同的,但是在实际聚类的过程中每维特征的贡献率是不同的。所以,本研究提出一种新的相似度测度方式,在每个向量的系数上加一个权重,关键就是权重的确定。此方法包括5个步骤。
步骤1:利用ARMA模型进行模型拟合,时间序列就会用一组系数向量表示。即:时间序列Xt和Yt拟合模型的参数向量分别为πX和πY。
步骤2:对系数向量进行标准化处理,然后以它们的欧氏距离作为相似度测量,用相应的方法聚类得到一个结果。同时,也会从结果中得到每位数据在聚类的过程中的贡献率为:(α1、α2、…、αn),n为拟合模型后系数的个数。
步骤3:找到累积贡献率达到一定比例的前m个系数的贡献率(α1、α2、…、αm),以此计算这 m个系数的权重(β1、β2、…、βm),i表示第i个系数

步骤4:把拟合模型参数向量的每维系数与相应的权重βi相乘,重新得到一个系数向量,则表示时间序列Xt的参数向量变为为μx。
步骤5:把新得到的系数向量进行标准化处理,以它们的欧氏距离为相似度测量,利用相应的聚类方法重新进行聚类,最终得到聚类结果。
2 ECG时间信号聚类
2.1 ECG信号
对ECG进行聚类是找出心律失常的重要手段。传统人工分析方法的诊断结果容易带有主观性成分,更重要的是面对成千上万个心拍和节律信息,完全依赖于人工诊断分析几乎不可能,也很容易造成错检或漏检。利用计算机对ECG信号进行自动分析,可以减轻工作负担,大大提高心律失常诊断的功能和精度。但是由于ECG信号本身具有的特点,没有一种算法可以完全适用于ECG的聚类,不断提高ECG的聚类效果成为研究热点。
数据来源于 MIT-BIH数据库的ECG信号。NSR(normal sinus rhythm,http://www.physionet.org/physiobank/database/nsrdb/)、PVC(premature ventricular contraction,http://www.physionet.org/physiobank/database/mitdb/),其信号的采样频率均为360Hz。其中,NSR信号数据包括18个样本,5名男性,年龄26至45岁,13名女性,年龄20至50岁。PVC信号数据包括25名男性,年龄32至89岁,22名女性,年龄32至89岁,其中有两个数据来自同一名男性患者,由于PVC信号数据库中两个ECG信号指标不统一。为此,我们仅选择了XLII信号和V1信号的病患者的数据,共40个样本。在MIT-BIH数据库信号数据中,最高信号量是MLII,其由电极放入胸部获得的;最低信号量通常是V1(偶尔是V2或V5),其也是由电极放入胸部获得的。不同种类的ECG信号有着不同的心跳率和RR周期。通常情况下NSR信号,其心跳率为60~100次/min。而PVC的RR间期比NSR的RR间期短,采用3 000个采样点的数据,已经包括了几个周期的ECG信号信息。
2.2 ECG信号的特征分析
从ECG的信号序列图看出正常窦性心律(NSR)和心室早期收缩(PVC)二者具有显著性差异,利用时间序列样本的自相关函数和偏自相关(即两个要素同时消除了其余要素影响后的相关)函数法对两种不同的ECG信号序列进行特征分析。
图1为正常窦性心律(NRS)的ECG信号的样本自相关函数(SACF)和样本偏自相关函数(SPACF)图。图(a)、(b)分别为MLII信号的SACF和SPACF图,图(c)、(d)分别为 V1信号的 SACF和SPACF图,从图可见MLII信号序列和V1信号序列均具有高度的自相关性。
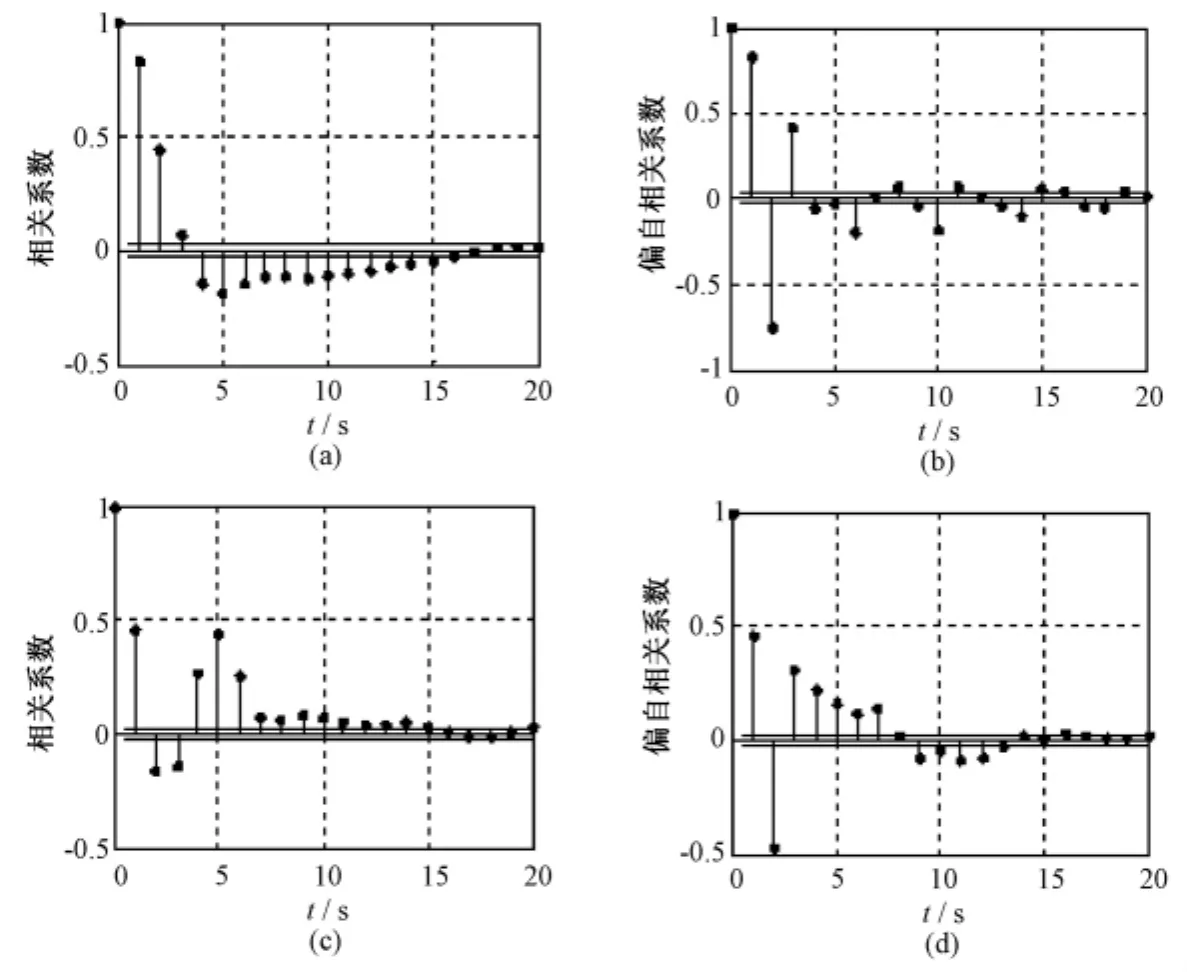
图1 正常窦性心律ECG信号的SACF和SPACF图。(a)MLII的自相关图;(b)MLII的偏自相关图;(c)V1的自相关图;(d)V1的偏自相关图Fig.1 The SACF and SPACF diagram of NSR ECG.(a)MLII SACF;(b)MLII SPACF;(c)V1 SACF;(d)SPACF

图2 心室早期收缩ECG信号的SACF和SPACF图。(a)MLII的自相关图;(b)MLII的偏自相关图;(c)V1的自相关图;(d)V1的偏自相关图Fig.2 The SACF and SPACF diagram of PVC ECG.(a)MLII SACF;(b)MLII SPACF;(c)V1 SACF;(d)SPACF
图2为心室早期收缩(PVC)患者的ECG信号的样本自相关函数和样本偏自相关函数图,得到其MLII信号序列和V1信号序列也具有高度的自相关性。统计结果表明ECG信号序列均适合采用ARMA模型进行拟合。
2.3 利用ARMA模型进行特征提取后聚类
2.3.1 将时间序列拟合ARMA模型
将NSR和PVC信号用于ARMA建模,引用了现有文献的方法和准则对包括PVC和NSR在内的每段心电信号进行ARMA建模。实验结果表明,AR过程和MA过程分别在P≥4和Q≥2时,信噪比随阶次的增加基本保持不变。在允许的范围内尽量减少计算的复杂度,选择P和Q分别为4和2。在P=4和Q=2时,各段ECG自相关系数≥0.99,这表明实际信号和仿真信号有着极强的相关性[12]。在本文中,我们选取58个测试样本的MLII信号和V1信号序列进行ARMA(4,2)拟合,利用ARMA的系数作为ECG信号的特征,则每一个样本可得12个特征值,前6个特征值是ECG的XLII信号拟合ARMA模型的参数估计结果,后6个特征值是V1信号序列拟合ARMA模型的参数估计结果。测试集一共有58个样本,前18个样品来自正常组(正常窦性心律,NSR),后40个样品来自非正常组(心室早期收缩,PVC)。
2.3.2 ECG信号的聚类分析
对每个样品来说,MLII和V1的ARMA(4,2)模型的参数的个数为12个,也就是对应的每个样本含有12个指标,下面利用离差平方和聚类法对这些样品进行聚类分析。
从表1的输出结果来看,各个指标变量之间的相关性较高。前3个主分量的累计贡献率已达81.61%,先利用主成分分析对ARMA(4,2)模型的系数降维,再利用离差平方和法进行聚类分析。聚类的结果显示可聚为两类,有23个不正常的样本(第1个字母为A)与18个正常的样本(第1个字母为N)归为一类,而另外17个不正常的样本自成一类,显然这种聚类错误率太高,说明直接利用ECG信号拟合ARMA(4,2)模型估计的参数作为特征进行聚类效果不是很好,需要对此方法进行相应的改进。
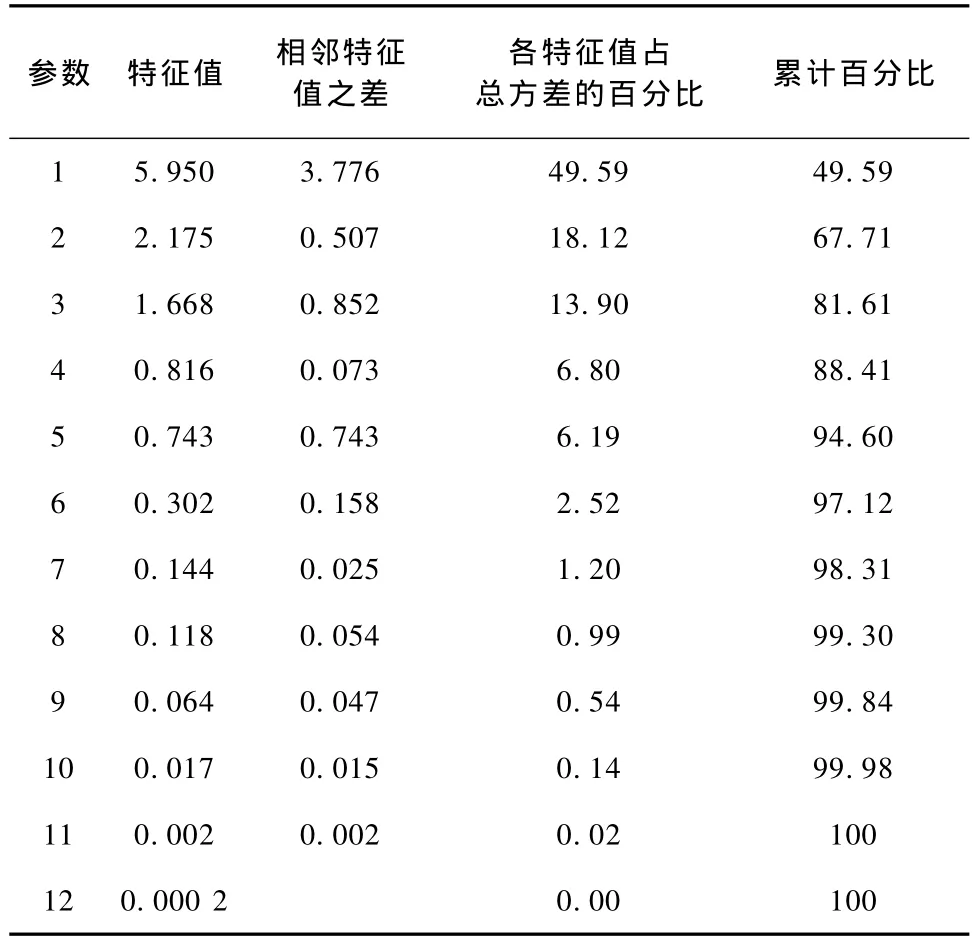
表1 ECG信号的聚类分析结果Tab.1 The result of clustering ECG
2.4 利用改进后的方法重新聚类
由表1的输出结果可以看出,前6个主分量的类计贡献率已经达到97.12%,所以选取前6个系数作为重新聚类的特征,计算出每个系数的权重分别为
β1=0.495 9/0.971 2=0.510 6
β2=0.181 2/0.971 2=0.186 6
β3=0.139 0/0.971 2=0.143 1
β4=0.068 0/0.971 2=0.070 0
β5=0.061 9/0.971 2=0.063 7
β6=0.025 2/0.971 2=0.025 9
对测试集每维特征的前6个系数进行加权,重新得到一组系数向量,利用最短距离聚类法进行聚类,结果如图3所示。

图3 利用改进的方法得到的ECG信号聚类树形图Fig.3 ECG clustering tree diagram with the improved method
由上图可以看出非正常组的样本22、30、20被分到了正常组,正常组的12被分到了非正常组,只有4个聚类错误,其他的划分都是正确的。表2是利用改进后的方法与未改进方法对ECG进行聚类的结果对比。由表中所示,对ECG信号而言,利用加过权重的ARMA模型系数作为特征进行聚类的精度明显提高。进而,表明所提出的权重确定方法法对聚类是有效的。
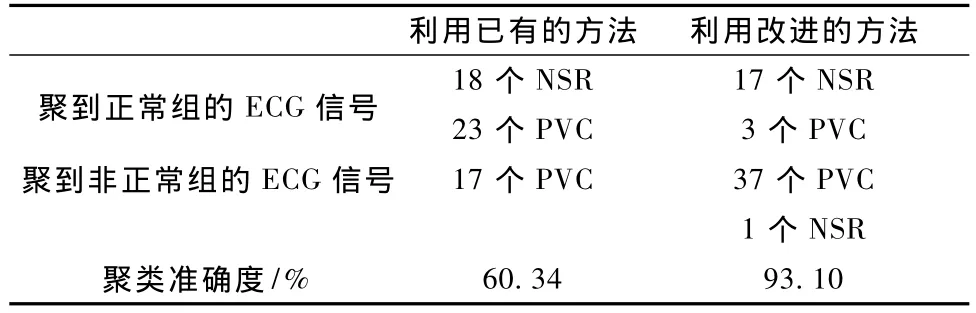
表2 两种方法聚类结果的对比Tab.2 The comparison of clustering results in two method
3 讨论和结论
对心电信号(ECG)进行聚类找出心律失常信号是医生诊断病症的方法之一,在各种心律失常中,心室早期收缩(PVC)最为常见。正确检测出PVC,是提高心律失常事件检测准确性的关键,也是本研究重点。采用了一种新的特征提取方法,对ECG信号模式识别之后,以它们拟合ARMA模型的系数作为聚类的前提,对每维系数进行加权,以它们的欧氏距离为结构不相似测度聚类。利用上述方法处理了MIT-BIH数据库的58个ECG信号,成功聚类54个,聚类的准确率达到93.10%,证明了所提权重确定方法的有效性。在已有研究的基础上作出了改进,实验的结果表现良好,证明此方法在ECG信号的聚类过程中是有效的,为聚类过程的实现找到了一种新的途径。但是仍然有4个聚类错误,最主要原因是拟合ARMA模型的阶数确定可能不够合理,从而导致提取的特征不能完全反映ECG信号的特点。不断改进ARMA模型的定阶方法,增加提取特征的代表性是今后研究的一个重要方向。
本研究对正常窦性心律(NRS)和心室早期收缩(PVC)两种ECG信号进行聚类分析,非正常的心电信号有多种,进一步的深化研究可把此方法运用在多种ECG信号的区分上。同样,也可把此方法运用到其他类型的时间序列分析当中,增加此方法的实践意义。
[1]Yeh Yun-Chi,Chiou Che-Wun,Lin Hong-Jhih.Analyzing ECG for cardiac arrhythmia using clusteranalysis[J].Expert Systems with Applications,2012,39(1):1000-1010.
[2]刘慧婷,倪志伟.基于EMD与 K-means算法的时间序列聚类[J].模式识别与人工智能,2009,22(5):803-808.
[3]曹玉珍,李广,范增飞.基于小波变换特征提取的支持向量机心搏分类研究[J].天津大学学报,2007,40(7):811-815.
[4]张灏.心律不齐ECG模式分类研究[D].上海:上海交通大学,2005.
[5]彭良瑞,杨振野,李玲华,等.基于单片机的实时室性QRS波分类方法的研究[J].中国医疗器械杂志,1997,21(3):133-135.
[6]Skordalakis E,Trahanias P.Syntactic pattern recognition of the ECG[J].IEEE Trans on Pattern Analysis and Machine Intelligence,1990,12(7):648-657.
[7]葛丁飞,李小梅.心电信号多周期融合特征提取和分类研究[J].中国生物医学工程学报,2006,25(6):645-649.
[8]Andreo RV,Muller SMT,Boudy J,et al.Incremental HMM training applied to ECG signal analysis[J].Computers Biology and Medicine,2008,38(6):659-667.
[9]尚宇,徐婷,何永辉.分数阶傅里叶变换在心电信号处理中的应用[J].电子科技,2012,24(8):116-118.
[10]杨荣峰,魏义祥.多级自组织映射用于心电信号QRS波群聚类[J].清华大学学报(自然科学版),2007,47(3):385-388.
[11]Gulera I,Ubeyh ED.ECG beat classifier designed by combined neural network model[J].Pattern Recognition,2005,38(2):199-208.
[12]翟晓,陈伟.一种计算简单的心电诊断算法的研究[J].传感技术学报,2007,20(4):731-734.
[13]孙吉贵,刘杰,赵连宇.聚类算法研究[J].软件学报,2008,19(1):48-60.

