弹目交会中破片命中点参数计算模型研究

王马法，李翔宇，卢芳云，龚柏林

（国防科学技术大学 理学院，长沙410073）

从上世纪70年代起，以美国为代表的一些国家对导弹遭遇段仿真技术进行了大量研究，并开发出了几种数字仿真系统[1，2]，如 FASTGEN、SCAN、SHASAM、IVAVIEW、OPEC、AMES 和 AMVS等.国内这方面的研究起步较晚，南京理工大学和中国工程物理研究院在这方面做了大量研究，并建立了各自的仿真计算平台[3～7].

弹目交会中命中点参数（包括命中点坐标、命中部位、命中数、破片落速、落角和命中时刻等）的计算是导弹遭遇段仿真技术中的关键技术之一.在传统的弹目交会仿真中，一般通过概率密度积分的方法求命中点参数，此方法计算精度较差，而且无法计算命中破片的落速、落角、命中点坐标等具体参数.王宏波[8]等提出了一种计算命中点参数的算法，该算法能够克服传统命中点参数计算方法的不足，但该方法没有考虑破片速度衰减对命中点参数的影响，且该方法在每个时间步长要对所有命中点参数进行遍历判断.庄志洪[9]等在相对速度坐标系中讨论了破片速度衰减对命中位置的影响.结果表明，在目标速度较低或者脱靶量较小时可以不考虑破片速度衰减的影响；反之，则需要考虑破片速度衰减的影响.鉴于空中目标具有高速运动的特性，在计算弹目交会命中点参数时，要计算得更加准确就必须考虑速度衰减的影响.

在弹目交会计算中忽略重力的影响，破片只受到空气阻力的影响.在相对速度坐标系中，即使只考虑空气阻力的影响，破片运动轨迹亦为曲线，这不利于讨论破片命中点.而在地面坐标系（原点在地面上的某一观察点）下观察，破片运动轨迹是一条射线（称为破片射线）.因此，在地面坐标系下讨论破片命中点参数有一定的优势.本文在地面坐标系下利用射线来描述破片轨迹，建立破片命中点参数计算的理论模型，并对解的存在范围进行讨论.该计算方法通过一次遍历即可求解整个战斗部破片对目标的命中点参数，而不需要在每个时间步长对目标面元和破片进行遍历.利用该模型讨论弹目交会参数和破片速度衰减系数对命中点参数的影响，为研究导弹遭遇段战斗部威力和目标易损性提供理论和技术支撑.

“一次遍历”是指，在战斗部起爆破片获得初速时，利用本文提出的计算模型，只需对所有破片进行一次循环即可确定每枚破片是否与目标有交点，如果有，则可以计算出该破片的命中点参数.

1 破片命中点精确计算模型

根据目标的几何参数，利用三角形面元对目标形体进行建模，如图1所示.

图1 目标三角面元模型

图1中每个三角形面元有3个顶点，面元的位置和法向可由3个顶点的坐标确定.如图2所示，△ABC为一面元，面元的法向由A、B、C三点确定为n′＝lAB×lAC，将n′单位化即可得到单位法向向量n.

破片与目标面元的交会过程如图2所示.在t0＝0时刻，破片所在位置为P点，破片射线与目标面元ABC所在平面交于点H；经过t1－t0时间后，破片从P点运动至P′点，面元ABC运动至A′B′C′，此时面元所在平面与破片射线交于H′.若存在某个时刻t＊使得P′与H′点重合，则说明破片会与面元所在平面有交点，通过破片运动轨迹即可求出该交点的坐标.再通过三角形面积法判断该点是否在三角形面元内，如果在面元内，则该点即为破片命中点.此时通过破片速度方向和面元法向量即可求出落角.下面对计算过程进行推导.

图2 单枚破片与目标面元的交会过程

1.1 破片飞行轨迹

以战斗部爆炸时刻为0时刻，破片的轨迹方程为

式中，s（t）为破片在t时刻所飞行的距离；vfn为破片速度方向的单位矢量；X为t时刻破片空间坐标，X0为0时刻破片的空间坐标.

根据文献[10]，破片在空气中飞行速度的衰减方程为vf＝v0exp（－αs），由此可以得到破片飞行距离与时间的关系为

式中，α为衰减系数；v0为破片初始速率；vf为破片在t时刻的速率.

1.2 目标面元所在平面的运动方程

在0时刻，目标某面元所在的平面方程为

式中，n为目标面元法向单位向量；D0为一标量常数，表示坐标原点到目标面元的距离；Y0为三角形面元中任意一顶点的初始坐标.由该面元在0时刻的3个顶点坐标即可求得n和D0的值.

假设在弹目遭遇段目标作匀速直线运动，且目标为刚体.因此，目标面元的运动也是匀速直线运动，且不会发生翻转，即面元只有平动，面元的法向不变，所以面元所在平面的运动方程可以表示为

式中，vt为目标在遭遇段的运动速度.

1.3 目标面元所在平面与破片射线交点的计算

目标面元平面与破片射线的交点H可由式（1）和式（4）联立解得：

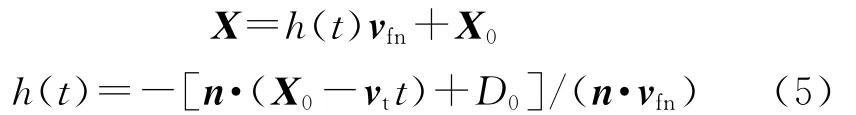
式中，h（t）为t时刻面元平面与破片射线交点到破片初始位置X0的距离.注意到式中n·vfn≠0.如果n·vfn＝0，则破片飞行方向与目标面元法向垂直，即与目标面元平行，因此不可能有交点，不再需要计算.

式（5）中的h（t）与式（2）中的s（t）不同，s（t）对应于图2中P点的运动轨迹，而h（t）则对应于H点的运动轨迹.将h（t）化为

式中，k＝（n·vt）/（n·vfn），h0＝－（n·X0＋D0）/（n·vfn），皆可以由弹目交会参数求出.

1.4 破片命中点参数的计算

若存在某时刻t＊使得s（t）＝h（t），即P′点与H′重合，则说明破片可以命中目标面元所在的平面.因此，求破片对目标面元的命中点，即要求解方程：

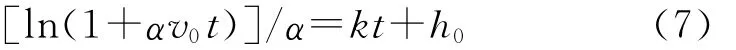
将该方程的解代入式（5）或式（1）求得命中点X＊的坐标：

通过破片速度方向向量、目标速度和面元方向向量求得落角：

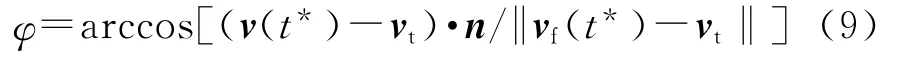
1.5 命中点是否在三角形面元内的判定

利用三角形面积法判断该命中点是否属于该目标面元.三角形面积法即判断某点与三角形任意两顶点面积之和是否等于该三角形的面积，如果等于则该点在三角形内，否则在三角形外.以图2中的△A′B′C′为例，判定下式：

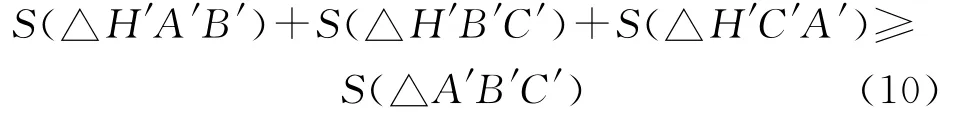
若取等号则H′位于三角形面元内，即破片命中该面元，并且以上获得的命中点参数即为该破片的命中点参数；否则，点H′位于面元外（即破片未命中该目标面元）.

由以上推导过程即可判断一枚破片与一个面元是否相交，并且求解该破片与该面元的交会参数.由此，通过对战斗部破片和目标面元的一次遍历即可求出战斗部与目标的所有命中点参数.

2 模型解分析

由计算模型可以看出，计算弹目交会命中点参数的关键是求解方程s（t）＝h（t），即式（7）是个超越方程，在数学上没有解析解表达式，但通过数值计算方法很容易求解.在方程中，对于每枚破片而言，α和v0为已知量，而k和h0则只能在交会过程中由破片和目标面元的信息共同决定，因此有必要对其作讨论.

2.1 k和h0的物理意义

从k的表达式k＝（n·vt）/（n·vfn）可以看出，它与面元法向、目标运动速度和破片速度方向有关，它代表目标面元平面与破片射线的交点H在破片轨迹直线上的运动方向和运动快慢.k＞0表示交点H与破片的运动速度方向相同，k＜0表示交点H与破片的运动速度方向相反.h0表示面元与破片初始时刻的位置关系，在图2中即为P点与H点的距离，h0＞0表示目标面元初始时刻在破片运动前方，h0＜0则表示目标面元初始时刻在破片运动后方.

2.2 k和h0取值关系

求解方程（7）等价于求解曲线s（t）和h（t）的交点，由方程可以看出两曲线的关系由直线的斜率k和截距h0决定.下面讨论k、h0的取值对解的影响.

1）当k＝0时.

此时n·vt＝0，即目标运动速度为0或者平行于面元，h（t）＝h0为一条平行于时间轴的直线，两条曲线关系示意图如图3所示.图中，y为破片运动轨迹上的点与破片初始点的距离.显然只有当h0＞0才有解且是唯一解，此时对应于目标在破片飞行的前方（当h0＜0时有一负解，由于0时刻为战斗部起爆时刻，所以该解为虚解）.其解为

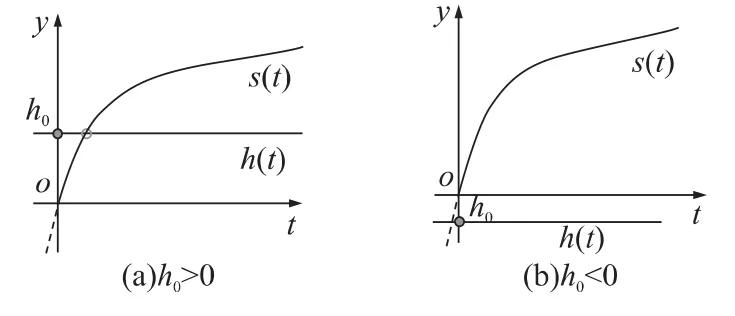
图3 k＝0时方程解示意图

2）当k＜0时.

此时面元平面与射线交点沿射线反方向运动，所以当其与破片作相对运动（即h0＞0）时两点一定会相遇，且存在唯一解.当h0＜0时，两点作相向运动，方程没有解.如图4所示.

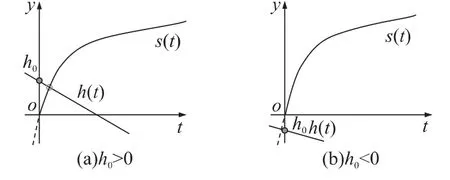
图4 k＜0时方程解示意图

3）当k＞0时.

此时两点的运动方向相同，是一个追赶问题.存在以下3种不同情况：①h0≤0，此时面元在破片后方追赶破片，随着破片速度衰减，总有一个时刻可以追赶上，如图5（a）所示.但这一过程时间比较长，此时破片速度已经衰减到不能忽略重力的影响，所以这种情况下虽然方程有解，但此解没有实际意义.②0＜h0≤[ln（v0/k）＋（k/v0）－1]/α，此时破片在后方追赶面元，两条曲线有2个交点，方程有2个解，两条曲线的相对位置如图5（b）所示.从实际碰撞情况出发，应该选择撞击时刻较小的解为方程的解.③h0＞[ln（v0/k）＋（k/v0）－1]/α，此时破片在后方追赶面元，但由于破片速度的衰减，破片将追不上面元，因此破片与面元没有交点，如图5（c）所示.

综上所述，方程的解只有以下3种情况：①k＝0，h0＞0；②k＜0，h0＞0；③k＞0，0＜h0≤[ln（v0/k）＋（k/v0）－1]/α.这3种情况分别对应准静止问题（包括目标静止或目标平行于面元运动）、迎头碰撞问题和追赶问题.

图5 k＞0时方程解示意图

3 速度衰减对命中点位置的影响

当衰减系数α＝0时，破片在空气中飞行速度为常数vf＝v0，由此得到s（t）＝v0t，将其替换式（7）等号左边，化为v0t＝kt＋h0，由此可解得破片与面元的交会时间t，进而可以求得命中点坐标.此即为不考虑速度衰减下破片命中点参数的计算方法.

从以上的分析可以看出，影响破片命中点参数的主要因素有目标运动速度、战斗部起爆瞬间导弹的运动速度、破片的静态飞散速度、破片的衰减系数和脱靶量等.图6～图9分别为不同衰减系数α、不同目标速度vt、不同静态破片初速v0和不同导弹速度vm下偏移距离与脱靶量ρ之间的关系.所谓偏移距离是指考虑与不考虑速度衰减的2种计算方法得到的2个命中点在目标上的距离，用lof表示.计算中将目标假设为一个40m×40m的巨大方形面元，面元中心即为目标中心.计算中采用的一组共同参数是：静态破片初速为2 000m/s，方向与战斗部轴线垂直；战斗部爆炸时刻导弹速度为900m/s；破片初速是静态破片初速与导弹速度的矢量叠加；破片速度衰减系数为0.000 15cm－1；目标速度为300m/s，目标速度与导弹速度平行，目标面元法线与目标运动方向垂直.即此时n·vt＝0，k＝0，对应了准静止问题.

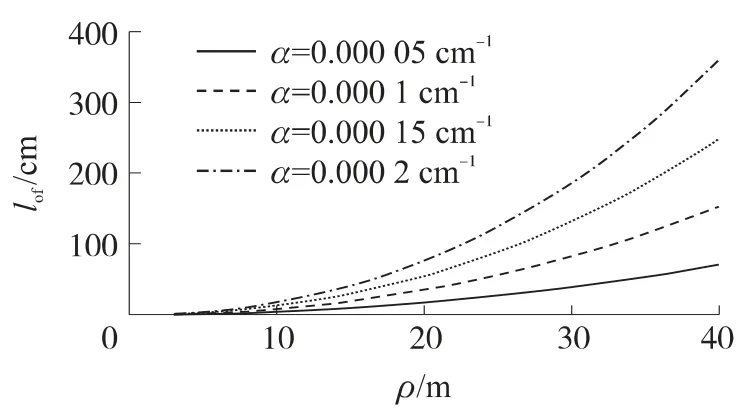
图6 不同衰减系数下脱靶量ρ对偏移距离的影响

图7 不同目标速度下脱靶量ρ对偏移距离的影响

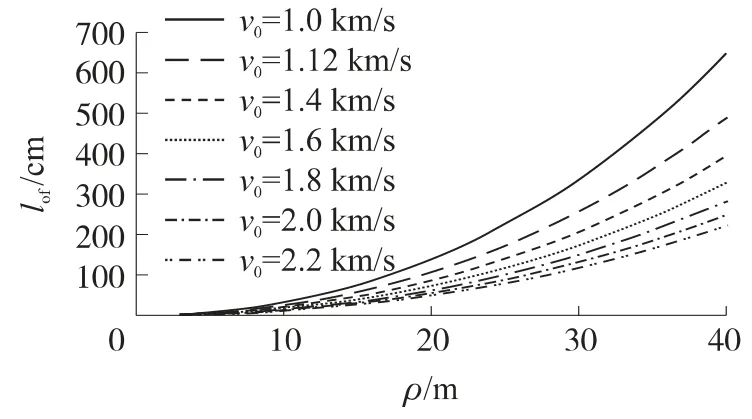
图8 不同静态破片初速下脱靶量ρ对偏移距离的影响

图9 不同导弹速度下脱靶量ρ对偏移距离的影响

从图6～图9可以看出，所有情况下偏移距离均随脱靶量的增加而增加.还可看出，在相同的脱靶量下偏移距离随破片速度衰减系数、目标速度和导弹速度的增加而增加，同时随静态破片初速的增加而减小.目标的运动速度和静态破片初速对命中点参数的影响比较大；导弹运动速度对破片偏移距离的影响很小，几乎可以忽略.

图7 中，目 标 速 度 为900m/s与 －900m/s、600m/s与－600m/s、300m/s与－300m/s的3组曲线重合，由此可以看出，对于准静止问题，不论导弹与目标是相向运动还是追赶运动，其偏移距离与脱靶量的关系不变.这是因为，对于准静止问题，不论是否考虑破片速度的衰减，在地面坐标系上破片的射线轨迹与目标面元始终交于同一个点.不同的是，考虑速度衰减下的破片速度变小，其到达交会点的时间与不考虑速度衰减的时间存在一个时间差，在这个时间差内，目标面元已经移动一定的距离，这个距离主要由目标速度大小决定，而与目标运动方向无关.

当采用的破片为Φ8mm的球形钢珠时，其在空气中的衰减系数为0.000 15cm－1.从图7可以看出，由于破片速度衰减造成的偏移距离随目标速度的增加和脱靶量的增大而迅速增加.如脱靶量为15m时，目标速度300m/s对应的偏移距离为0.30m，目标速度600m/s对应的偏移距离为0.60m，目标速度900m/s对应的偏移距离为0.91m；脱靶量为20m时，目标速度300m/s对应的偏移距离为0.55m，目标速度600m/s对应的偏移距离为1.10m，目标速度900m/s对应的偏移距离为1.66m.因此，对于尺寸较小或者高速运动的目标，在计算命中点参数时必须考虑破片速度的衰减，否则主破片束将偏离目标关键部件，这大大减小毁伤概率.

4 结论

①本文提出了一种精确计算弹目交会中破片命中点参数的理论模型，该模型可以通过一次遍历计算得到导弹与目标的所有交会参数.

②对模型解的存在范围进行讨论，获得了解存在的3种条件，分别为k＝0，h0＞0；k＜0，h0＞0；k＞0，0＜h0≤[ln（v0/k）＋（k/v0）－1]/α.这3种情况分别对应准静止问题（包括目标静止或目标平行于面元运动）、迎头碰撞问题和追赶问题.

③目标的运动速度和静态破片初速对命中点参数的影响比较大；战斗部起爆时刻导弹运动速度对命中点参数的影响较小.

④对于尺寸较小或者高速运动的目标，在计算命中点参数时需要考虑破片速度的衰减，否则主破片束将偏离目标关键部件，这大大减小毁伤概率.

[1]徐豫新.破片杀伤式地空导弹战斗部杀伤概率计算[D].太原：中北大学，2008.XU Yu－xin.Simulation of damage probability on the fragment air－defence warhead[D].Taiyuan：North University of China，2008.（in Chinese）

[2]BUSH J T.Visualization and animation of a missile/target encounter，AD－A336994[R].1998.

[3]谢传波.轴向增强战斗部对空目标毁伤效果的仿真研究[D].南京：南京理工大学，2006.XIE Chuan－bo.Simulating research on the damage effect of the axial forward enhanced warhead to air－target[D].Nanjing：Nanjing University of Science and Technology，2006.（in Chinese）

[4]张学锋.火箭武器防空反导效能研究与系统仿真[D].南京：南京理工大学，2006.ZHANG Xue－feng.Research on the capability of rocket air－defense system and its system simulation[D].Nanjing：Nanjing University of Science and Technology，2006.（in Chinese）

[5]宗丽娜.便携式反直升机火箭弹引战配合的计算机仿真研究[D].南京：南京理工大学，2006.ZONG Li－na.Simulation research on fuze－warhead coordination of anti armed helicopter portable rocket bomb[D].Nanjing：Nanjing U－niversity of Science and Technology，2006.（in Chinese）

[6]刘彤.防空战斗部杀伤威力评估方法研究[D].南京：南京理工大学，2004.LIU Tong.Research on the lethality assessment method of anti－air warhead[D].Nanjing：Nanjing University of Science and Technology，2004.（in Chinese）

[7]卢永刚，钱立新，杨云斌，等.目标易损性/战斗部威力评估方法[J].弹道学报，2005，17（1）：46－52.LU Yong－gang，QIAN Li－xin，YANG Yun－bin，et al.Vulnerability/lethality assessment method based on virtual model[J].Journal of Ballistics，2005，17（1）：46－52.（in Chinese）

[8]王宏波，庄志洪，张京国.引战配合可视化仿真命中点参数精确计算[J].系统仿真学报，2010，（4）：1 071－1 074.WANG Hong－bo，ZHUANG Zhi－hong，ZHANG Jing－guo.Accurate calculation of hitting point parameters in visual simulation of fuze－warhead coordination[J].Journal of System Simulation，2010，（4）：1 071－1 074.（in Chinese）

[9]庄志洪，路建伟，张清泰，等.破片速度衰减对命中目标部位的影响[J].弹道学报，1999，11（2）：5－8.ZHUANG Zhi－hong，LU Jian－wei，ZHANG Qing－tai，et al.Effects of fragments velocity fade on hitting position[J].Journal of Ballistics，1999，11（2）：5－8.（in Chinese）

[10]庄志洪，张清泰.求解战斗部最佳起爆时机的一种方法[J].现代引信，1997，（1）：10－16.ZHUANG Zhi－hong，ZHANG Qing－tai.A solving method of warhead optimum detonating time[J].Journal of Detection and Control，1997，（1）：10－16.（in Chinese）