基于线阵像机的弹丸速度与姿态测量
回丙伟,赵竹新,文贡坚
(国防科学技术大学ATR重点实验室,长沙410073)
线阵像机以及传统的胶片式狭缝摄影机作为一类独特的光学成像设备,能够对经过其视平面的目标进行扫描成像,记录目标在一个极短时间段内的速度和姿态信息,因而在弹丸的攻角测量中具有不可替代的作用[1~5].由于早期的狭缝摄影机参数难以标定,从而无法从摄影几何的角度建立严格的数学成像模型,导致传统测量方法通常在一定近似条件下进行.这对提高测量的精度极为不利,同时胶片式摄影机复杂的操作过程对靶场测量人员要求较高[2].近年来随着光电子和计算机技术的发展,一方面线阵像机成像速度越来越高,并以数字化和自动化的突出优点逐步替代胶片式狭缝摄影机;另一方面研究人员对线阵像机的成像模型研究越来越多,线阵像机参数标定技术日趋成熟[6,7],这为在严格线阵像机成像方程下研究目标的运动与姿态参数测量方法奠定了基础.本文在这种背景下开展了线阵像机靶场测量方法的探索和研究.
为获得稳定的三维测量结果,测量中常采用交会摄影法获取多视角图像.根据线阵像机视场位于一个平面内这一特性,实际中常采用镜面反射法获取待测弹丸的立体图像,如图1所示.在弹丸飞行轨迹的下方,放置一个大约与水平面成45°的平面镜,当弹丸从平面镜上方飞过时,弹丸本身和弹丸在平面镜中的像都能在该线阵像机中成像.上述方法实现了使用一个线阵像机从2个视角获取目标立体图像的目的[8].这种测量方式涉及3个坐标系:①测量坐标系OXYZ,各测量参数均在该坐标系下描述,是测量的基准坐标系;②像机坐标系sxyz,目标特征点的像点坐标在该坐标系下已知,且该坐标系相对于测量坐标系OXYZ的相对方位关系在经过标定后已知;③目标坐标系ox′y′z′,目标上特征点的三维坐标在该坐标系下已知,该坐标系相对于测量坐标系OXYZ的方位关系在本文中是待求参数.下文中,将目标上的一个特征点和其对应的图像点称为一对控制点.

图1 利用一个线阵像机获取立体图像的方法
在摄取到弹丸目标的线阵立体图像后,基于多对控制点和成像方程,联立一组以弹丸速度、姿态和初始位置8个参数为未知数的非线性方程组,并进行最优化建模.在对模型求解的过程中,首先利用Powell算法对非线性的姿态参数进行搜索,同时使用线性方程组对位置和速度参数进行求解,并在搜索过程中,对优化模型的目标函数值不断寻优得到测量初值;然后进一步使用Gauss-Newton法进行精确迭代求解.
1 线阵像机测量原理与成像方程
静态场景中,线阵像机成像可以看作面阵像机成像的一种特殊情况,只有位于线阵传感器与主光轴所构成的平面(即视平面[6])内的场景,能够按中心投影原理成像.在sxyz中描述,即x≡0,y方向满足中心投影方程[9]:
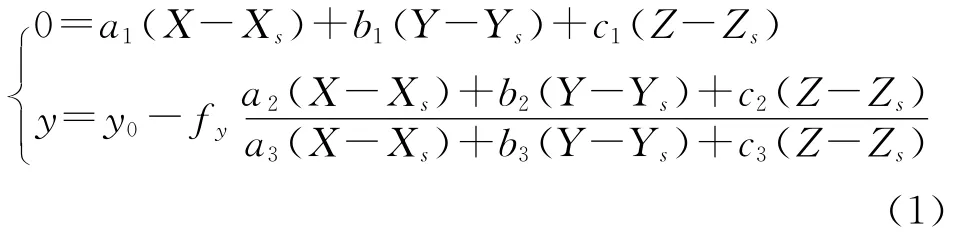
式中,(X,Y,Z)为场景中一点在OXYZ中的空间坐标,y为对应的像点坐标.Xs,Ys,Zs为像机摄影中心在OXYZ中的坐标;旋转矩阵元素al,bl,cl(l=1,2,3)是由像机外参数姿态角φ,ω,κ决定的.y0为像主点位置,fy为像机主距,y0、fy统称为像机内参数.
式(1)的第1式即为视平面的方程,由该式可得:
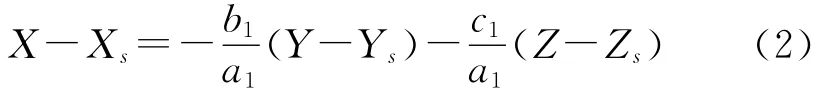
将式(2)代入式(1)中第2式,并根据旋转矩阵的性质进行化简,得到线阵像机的静态成像方程:

将每一条成像线按时间顺次排列成一幅二维图像,即为线阵像机的动态成像结果,以下称之为线排列图像.通常可以认为弹体在经过线阵像机视平面的过程中是保持固定姿态匀速运动的,下面推导该过程中弹体表面点的动态成像方程.
一般三维刚体目标的空间姿态需要用3个空间旋角来表达.由于绝大多数的弹丸目标都具有旋转体的几何结构,因此沿弹丸中轴线的自转角不用考虑,此时其空间姿态通常使用目标绕2个指定坐标轴(本文中即为目标坐标系的y′轴和z′轴)的2个空间旋转角α和β来描述.并设某一时刻在OXYZ中,目标坐标系原点的坐标为(Xo,Yo,Zo),运动速度矢量v=(vX vYvZ);线阵像机的成像频率为ν;假设目标坐标系中一点(x′,y′,z′)在线阵像机的第n次成像时被捕获;像机相邻两次成像间隔t=n/ν;并记(DX DY DZ)=(vX/νvY/νvZ/ν).可得目标点(x′,y′,z′)在经过线阵像机瞬间的空间坐标(X,Y,Z)为[8]
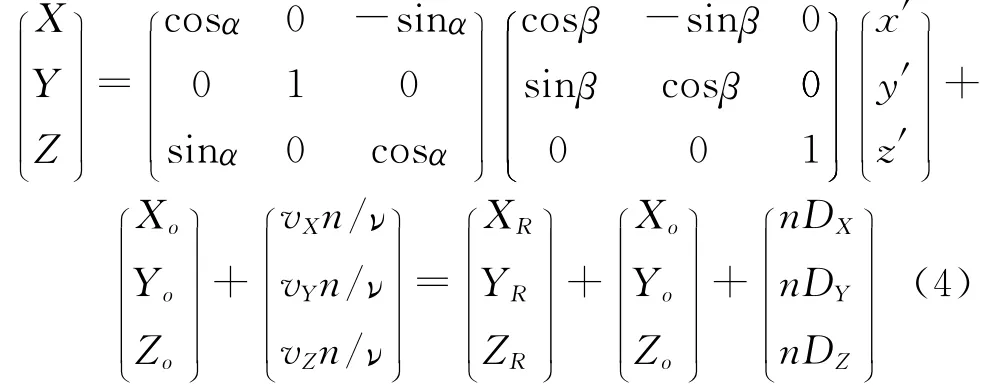
式(4)表明,能在线阵像机中成像的弹丸表面点的空间坐标由三部分确定:弹丸的姿态角α,β决定的(XR,YR,ZR);初始位置时刻弹丸的目标坐标系原点在OXYZ中的坐标(Xo,Yo,Zo);弹丸的速度(vX,vY,vZ)决定的(nDX,nDY,nDZ).因此该式包含了全部待求参数.将式(4)代入式(3),并变换其中的约束条件方程得弹丸目标的动态成像方程:
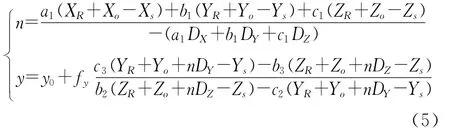
结合平面镜成像原理,目标点(x′,y′,z′)的镜像点在OXYZ坐标系中的坐标为
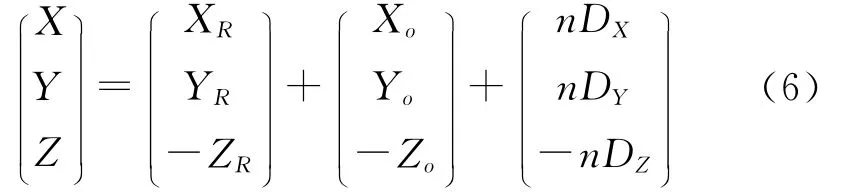
同理将式(6)代入式(3)可得:

因此在上文的假设前提下,式(5)与式(7)分别描述了弹丸目标上任意一点及其平面镜中的虚像点与各自其图像点的对应关系.基于这样一种严格几何成像关系,本文以α,β,DX,DY,DZ,Xo,Yo,Zo为未知量实现弹丸各项参数的测量.
2 速度与姿态测量
2.1 特征点选取与最优化模型
在本文中,弹丸的速度与姿态参数的测量本质上是利用若干对控制点,求解一个含有8个未知数的非线性方程组.由动态成像方程式(5)或式(7)可知,一对控制点可以建立2个方程.因此方程组可解的条件要求至少存在4对控制点.由于弹丸目标在飞行状态时高速旋转,其表面的特征点在线排列图像中通常难以正确识别.而比较稳定的特征点是弹尖和弹尾等特殊点,如图2所示.

图2 线排列图像中弹丸上特殊点的选取
对于弹尖上的控制点,无论在图像中还是在目标中都是容易确定的;而对于弹尾上来说,图像上容易识别的上下两个端点(图2中的弹尾A和弹尾B)却在目标坐标系中难以确定,因此本文选择弹尾的中心点作为控制点,在图像中表现为A、B两点连线的中点.这样从2个视角拍摄的弹丸图像中可以确定4对控制点,可以满足方程求解的基本条件.足够数量的控制点是实现本文测量方法的必要条件.
多元非线性方程组的求解,可根据最小二乘原理转化为非线性最优化模型来描述.假设目标表面有N个特征点,(i=1,2,…,N,N≥4),在线阵像机中所成的像点为(ni,yi).利用(x′i,y′i,z′i),根据一组参数Φ=(αβDXDYDZXoYoZo),按式(5)或式(7)计算的投影点 坐 标).若 参 数 向 量Φ能 使(ni,yi)与满 足 最 优 化 目 标 函 数 时,即 为 方 程 组 的唯一解:
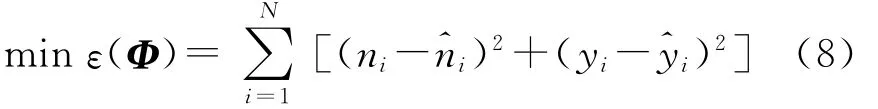
对于式(8)的最优化数学模型,Gauss-Newton法是解决这类问题的经典方法,但对于高维的优化问题,通常需要为其提供一个较好的初值,本节根据模型的特点,利用Powell算法搜索待测参数的近似初始值,然后进一步使用Gauss-Newton迭代法精确求解.
2.2 初值搜索
对于式(5)或式(7)组成的方程,若已知参数α,β,可将其代换为

式中,lgh,mgj,ng(g=1,2;h=1,2,…,6;j=1,2,3)均可根据目标上特征点在ox′y′z′中的坐标和像机参数等已知量进行代数换算,(XR,YR,ZR)在给定α,β值的情况也为已知量,因此式(9)是关于6个待求参数DX、DY、DZ、Xo、Yo、Zo的线性方程.利用这一特性和解的唯一性,本文通过对α、β进行搜索,并对每一给定值的α(k)、β(k),利用原方程组解算线性参数,并 寻 找 一 组 参 数在目标函数式(8)的度量下达到最小值,此时可认为其近似为方程组的解.因此,在式(9)的约束下,可认为式(8)的目标函数是关于α、β求极小值的问题.图3显示了某次测量中,目标函数值与α、β的关系.为直观地表现目标函数的极小值,绘图时对目标函数进行对数变换,这并不影响函数的单调性.
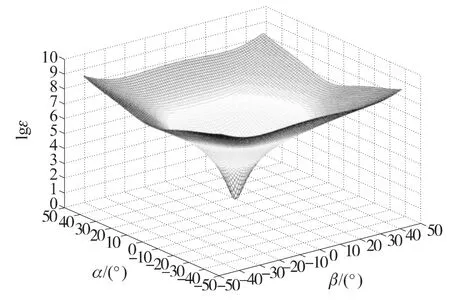
图3 目标函数值的对数与α、β的关系
下面考虑使用快速的搜索算法使目标函数能在任意α、β初值情况下,快速收敛到极小值,该值即为待测参数的一组近似解.Powell算法是一种不涉及目标函数导数的最优化搜索算法,它是以正定二次函数为背景,以共轭方向为基础的最优化问题直接搜索方法.该方法具有良好的模块化特性,已经在许多工程领域获得了广泛的应用,本文以Powell算法为基础搜索方程解的近似值,具体过程如下:
①首先任意设定待求参数初值α(0)、β(0);
②进入Powell搜索,然后按照算法的搜索规则寻找目标函数极小值,并在第k次搜索中,先将α(k)、β(k)代入式(9),利用线性最小二乘法计算
③将α(k),β(k)代入式(8)计算当前目标函数值ε(k);
④重复上述步骤②和步骤③直到最终输出α,β,DX,DY,DZ,Xo,Yo,Zo满足精度的测量值.
虽然本节Powell搜索中使用的目标函数是按最小二乘的形式定义的,但并不是所有的参数都统一参加了最小二乘平差计算,因此,其搜索结果并不是最小二乘意义下的最优解,下一节将使用严格最小二乘迭代求解其精确解.
2.3 迭代求解
根据最小二乘原理,将N个特征点在ox′y′z′中的坐标(x′i,y′i,z′i)视为真值,而 把 相 应 的 图像点坐标(ni,yi)视为观测值,对于每一个特征点通过将式(5)或式(7)进行一阶泰勒展开,列各点的误差方程式为
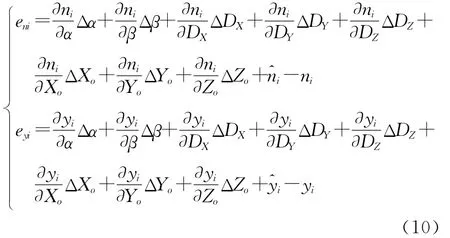
式(10)用矩阵形式表示为

式中,

若有N对控制点,则可按式(11)列出N组误差方程式,共同构成总的误差方程式:

式中,E=(E1E2…EN)T,A=(A1A2…AN)T,L=(l1l2…lN)T.
根据最小二乘平差原理,可以得到待求参数近似值的改正量:
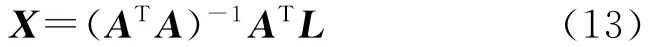
由于式(10)中的各系数取自泰勒级数的线性展开,因此迭代计算通过逐渐趋近的方法,即用原近似值与式(13)求得的改正量的和作为新的近似值,重复上述过程,直至改正量各分量的绝对值小于某一个设定的极限值为止,最后得到待求参数的解.
在得到DX,DY,DZ的精确迭代结果后,弹丸速度(vXvYvZ)=(νDXνDYνDZ).
3 仿真实验
为验证上述方法的测量精度,本文对不同像机参数下,不同弹丸几何尺寸和不同的运动姿态参数进行了大量图像仿真和测量实验,下文以一组实验为例进行说明.
首先利用3dMax创建了一个弹长550mm,弹径70mm的弹丸目标三维表面模型;然后利用第1节线阵像机的成像原理对弹丸飞过像机视场时进行8次仿真成像,每次成像中弹丸运动与姿态参数如表1所示,像机主机像素为fy=5 000,y0=0,线阵像机成像速度ν=140 000s-1.像机外参数如表2所示.

表1 仿真中弹丸目标速度与姿态参数设定值

表2 线阵像机外参数
使用上面第1节与第2节的测量方法,分别对仿真得到的图像进行测量.对合速度参数v和2个姿态参数分别进行精度比较,如表3所示,表中v为利用表1中的3个速度分量计算所得的合速度的理论值;v′,α′,β′为弹丸合速度与姿态参数的测量值.

表3 弹丸速度与姿态参数测量值
由表3的测量结果对比表1可知,合速度的相对测量误差小于2%,姿态的测量最大误差小于0.4°,平均偏差为0.20°.
4 结论与展望
在本文的测量方法中,弹丸目标的初始时刻在测量坐标系中的位置Xo、Yo、Zo,并不是待求参数,但是为了能够从严格投影方程的角度来分析弹丸的运动和姿态,该参数向量的引入是有必要的.
本文利用成像方程和从目标表面选取的若干个特征点建立了以目标的初始位置、速度和姿态参数共8个未知量的非线性方程组.通过将方程组的求解问题进行最优化建模和求解,实现了各参数的测量.在求解过程中,首先利用了方程组中大量参数是线性的这一特性,以Powell搜索为基础,同时利用原方程对线性参数进行求解,得到了方程组的一组近似解;然后进一步使用Gauss-Newton迭代法对待求参数进行精确求解.本文方法的优势体现在:①将线阵像机的严格成像方程引入弹丸姿态参数的测量中,使测量方法有严格的理论依据;②在严格成像模型下,给出了基于特征点坐标的弹丸目标初始位置、速度和姿态参数的解算方法.
考虑到像机镜头的光学畸变,在图像预处理的过程中根据像机标定所得的径向与切向畸变系数进行预先矫正,因此本文在对像机成像模型的讨论中并未涉及畸变模型.
在具体的靶场实践中采用本文测量方法,可能为测量引入较大的误差的因素主要有:①目标在经过线阵像机视平面过程中的匀速特性;②像机成像中的积分时间带来的图像点模糊;③人工拾取特征点的不确定性.量化研究并尽量消除上述因素对测量精度造成的影响是下一步需要研究的重点内容.此外,本文测量方法只针对具有旋转体结构的弹丸目标而设计,而对于一般结构的三维目标,由于其空间姿态需要3个空间旋转进行描述,在使用本文测量基本原理的情况下,需要为之设计新的解算方法.
[1]高昕,王建军,汤阳.利用狭缝相机实现弹丸攻角高精度测量研究[J].飞行器测控学报,2004,23(1):69-72.GAO Xin,WANG Jian-jun,TANG Yang.Precision measurement of nutation angle using slit cameras[J].Journal of Spacecraft TT & C Technology,2004,23(1):69-72.(in Chinese)
[2]张三喜,薛以辉,卢宇.狭缝摄影胶片图像运动参数测量和处理[J].光子学报,1999,28(12):1 117-1 121.ZHANG San-xi,XUE Yi-hui,LU Yu.The measuring and processing of streak camera’s image motion parameters[M].ACTA Photonica Sinica,1999,28(12):1 117-1 121.(in Chinese)
[3]LI J K,CHEN L Y.A slit photography system based on linear CCD[J].Laser &Infrared,2009,39(3):300-303.
[4]SONG W D.Software design for measurement of bullet attitude based on linear CCD[C].9th International Conference on Electronic Measurement and Instruments.Xi’an:CIE,2007:521-524.
[5]HUGHETT P.Projectile velocity and spin rate by image processing of synchro-ballistic photography[C].Ultrahigh-and High-Speed Photography,Videography,Photonics and Velocimetry.San Diego:SPIE,1990:237-248.
[6]RADU H,ROGER M,BOGUSLAW L.On Single-scanline camera calibration[J].IEEE Transactions on Robobtics and Automatic,1993,9(1):71-75.
[7]LUNA C A,MAZO M,LAZARO J L.Calibration of line-scan camera[J].IEEE Transactions on Instruementation and Measurement,2010,59(8):2 185-2 190.
[8]冯文灏.近景摄影测量——物体外形与运动状态的摄影法测定[M].武汉:武汉大学出版社,2007:72-73.FENG Wen-hao.Close-range photogrammetry(measurement of object’s facade and motion)[M].Wuhan:Wuhan University Press,2007:72-73.(in Chinese)
[9]WANG Zhi-zhuo.Principles of photogrammetry[M].Press of Wuhan Technical University of Surveying and Mapping &Publishing House of Surveying and Mapping of Beijing,1990:18-19.

