随机风场与升阻比误差对空空导弹可攻击区的敏感度研究

吴胜亮，南 英，黄国强，华 鹏，李 鑫

（南京航空航天大学 航天学院，南京210016）

空空导弹可攻击区受众多因素的综合影响，主要影响因素有空空导弹发动机推力、气动力特性、质量特性、制导导航与控制系统、目标机动与飞行速度、大气（风场）特性及发射点状态等.文献[1]针对离轴发射空空导弹进行仿真研究，分析了空空导弹发射条件（目标进入角、目标过载、作战高度、目标速度、导弹初始速度、导弹初始离轴角）的改变对空空导弹发射包线的影响，并提出了用导弹发射包线灵敏度系数来反映发射包线与操纵参数的关系；文献[2]针对飞机的三轴方向提出了敏捷性矢量的估算方法，并研究了飞机敏捷性对导弹可攻击区的影响规律；文献[3]将带推力矢量控制与不带推力矢量控制的空空导弹攻击区进行对比，分析了推力矢量控制对空空导弹攻击区的影响；文献[4]具体分析了空空导弹发射高度、发射初速度、发射角度对空空导弹攻击区的影响；文献[5]研究了4种目标机动类型（水平面等速直线运动、水平等过载机动、垂直面等过载爬升、等过载横滚）对空空导弹攻击区的影响.

本文研究空空导弹加工误差引起的升阻比误差、大气风场干扰对空空导弹可攻击区的影响.考虑到升阻比误差与风场干扰，采用某空空导弹模型与三维空间的比例导引律，通过大规模系统的导弹与目标对抗飞行轨迹仿真，迭代出了不同条件下的空空导弹可攻击区.通过大量的可攻击区数据库，研究了干扰源（风场、升阻比误差）对该空空导弹可攻击区的敏感度.

1 问题的描述

针对空空导弹三维可攻击区，求出三维可攻击区边界相对其确定因子随机风场的敏感度εμ、ημ、ξμ、ζμ和升阻比误差的敏感度ελ、ηλ、ξλ、ζλ如下：

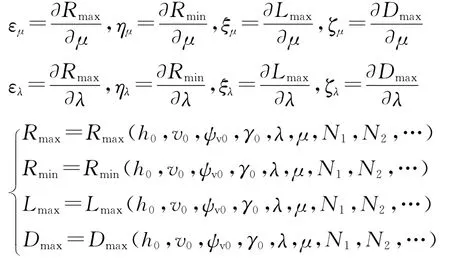
式中，Rmax为攻击区的远边界，Rmin为攻击区的近边界；Lmax为攻击区的左侧边界，Dmax为攻击区的右侧边界；h0，v0，ψv0，γ0分别为空空导弹初始发射时刻的高度、速度、轨迹偏角和轨迹倾角；λ、μ分别为空空导弹总体模型中的升阻比、风速方向的角度；N1，N2，…为其它限制条件，如导弹最大可用过载、导弹推进系统、目标最大机动过载等.

2 空空导弹攻击区计算模型

2.1 空空导弹运动数学模型

导弹的6－D运动微分方程[6]为

式中，X（t）＝（vγψvhxzωxωyωzΓφφαβσ）为导弹飞行状态；v，γ，ψv分别为导弹的速度、轨迹倾角和轨迹偏角；h，x，z分别为导弹所在的高度、经度方向上的距离和纬度方向上的距离；α，β，σ分别为导弹迎角、侧滑角和滚转角；ωx，ωy，ωz分别为绕弹体x，y，z三轴的转动角速度；Γ，φ，φ分别为与ωx，ωy，ωz相对应的欧拉角；控制变量U（t）＝（δxδyδz），即导弹气动舵偏角；导弹的系统参数Pm＝（CxCyCzFpS）；Cx，Cy，Cz分别为导弹的阻力系数、升力系数和侧力系数；Fp为发动机的推力；m为导弹的质量；为导弹的质量消耗率；S为导弹的特征面积；W（t）为风场的加速度与速度；目标飞行状态Xt（t）＝（vtγtψvthtxtzt）参见目标数学模型；t为导弹（目标）的飞行时间.

2.2 导弹制导律数学模型

空空导弹采用三维空间的比例导引律.比例导引律下，空空导弹指令加速度为

式中，ay，az分别为俯仰加速度和偏航加速度；κ为比例系数；为目标相对导弹的距离变化率；y，z分别为空空导弹与目标连线（LOS）的旋转角速度在地面坐标系y轴和z轴上的分量.

2.3 导弹的气动力模型与推进系统模型

升力系数Cy和升阻比λ随飞行马赫数Ma、攻角α的变化，如图1、图2所示.

图1 Cy随Ma和α的变化

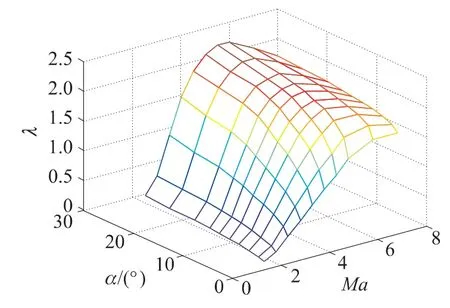
图2 λ随Ma和α的变化

在发动机工作期间（10s之内），推力Fp＝7kN，质量消耗率＝20kg/s.

2.4 目标运动数学模型

目标飞行运动微分方程[6]：

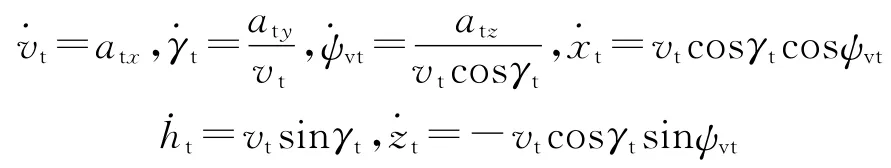
式中，下标t代表目标，at为目标在笛卡尔坐标系下的机动加速度.通过设立目标飞行加速度（atx，aty，atz）随时间变化的函数，即可产生不同类型的任意4－D 机动突防飞行轨迹（t，ht，xt，zt）.

2.5 三维风场模型

三维风场的加速度与速度为

三维风场数学仿真模型由统计数据[7，8]描述，也可以根据当地气象部门实时在线给出气象风场信息.风速与风切变awy随高度的变化而变化，如图3所示，风速的方向如图4所示.

图3 风速随高度变化

图4 风速的方向定义

在水平面内，风切变模型为awx＝0，awz＝0.

3 数值仿真与分析

针对随机风场与升阻比误差对导弹攻击区的影响，进行了大规模的空空导弹与目标相互对抗的数值仿真，得到了大量的空空导弹3D可攻击区.该3D可攻击区的数值仿真计算条件为：空空导弹和目标迎击时的情况，导弹（发射点）初始位置均为（0，10km，0），初始飞行速度均为300 m/s；目标保持匀速直线飞行，飞行速度为300m/s.

基于大量的空空导弹3D可攻击区的数值仿真结果，可以得到可攻击区边界对风速方向与升阻比误差的影响与敏感度，如下所述.

3.1 风场对空空导弹3D可攻击区的影响

导弹攻击区相对（图3与图4所示的三维风场模型）风速方向μ的敏感度如图5所示.其中一些详细的风场对空空导弹3D可攻击区的影响可参见图6～图9.

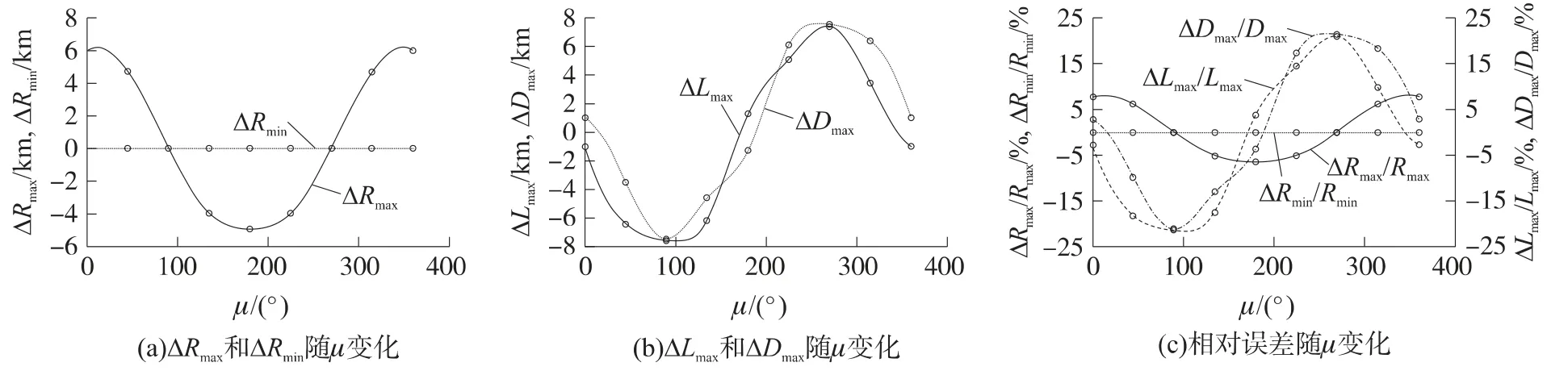
图5 敏感度随风向μ变化曲线

图6 无风与μ＝0°可攻击区的比较

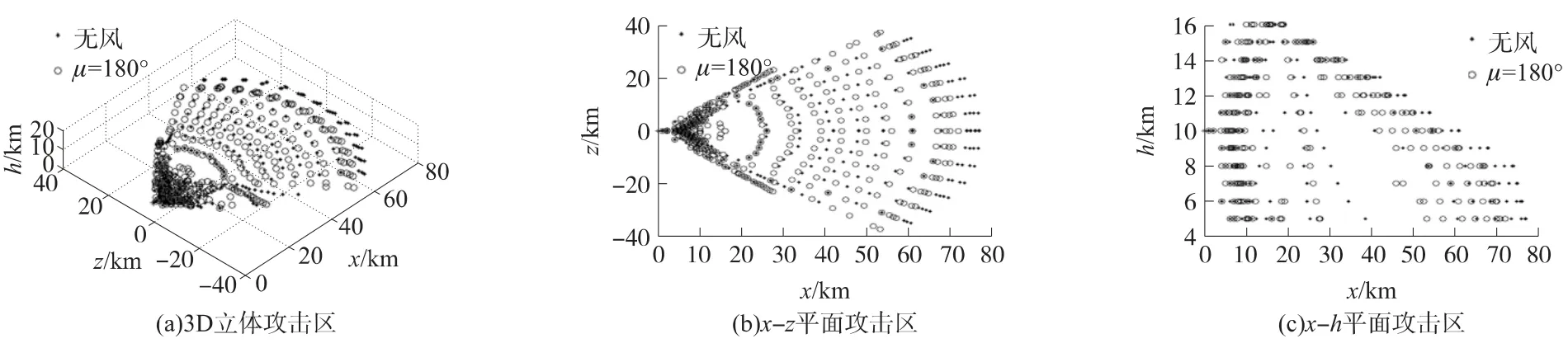
图7 无风与μ＝180°可攻击区的比较

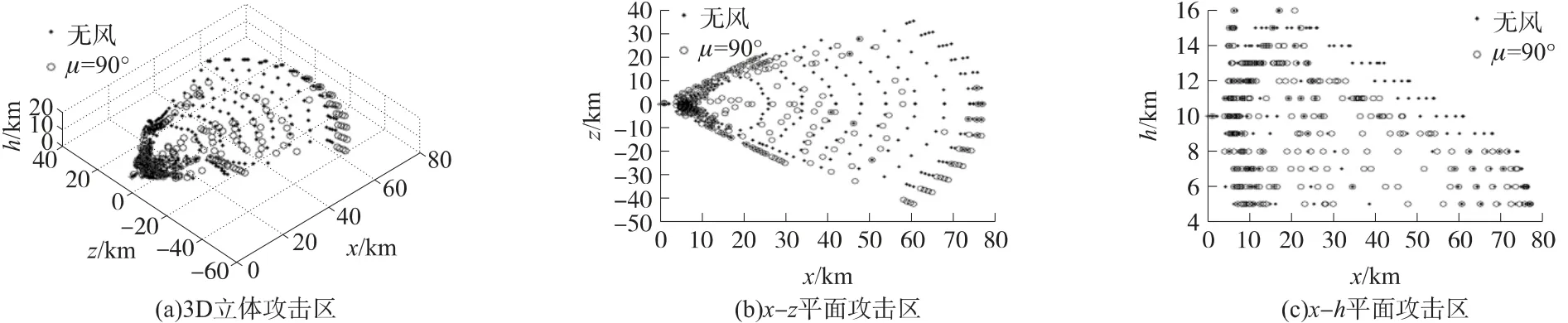
图8 无风与μ＝90°可攻击区的比较

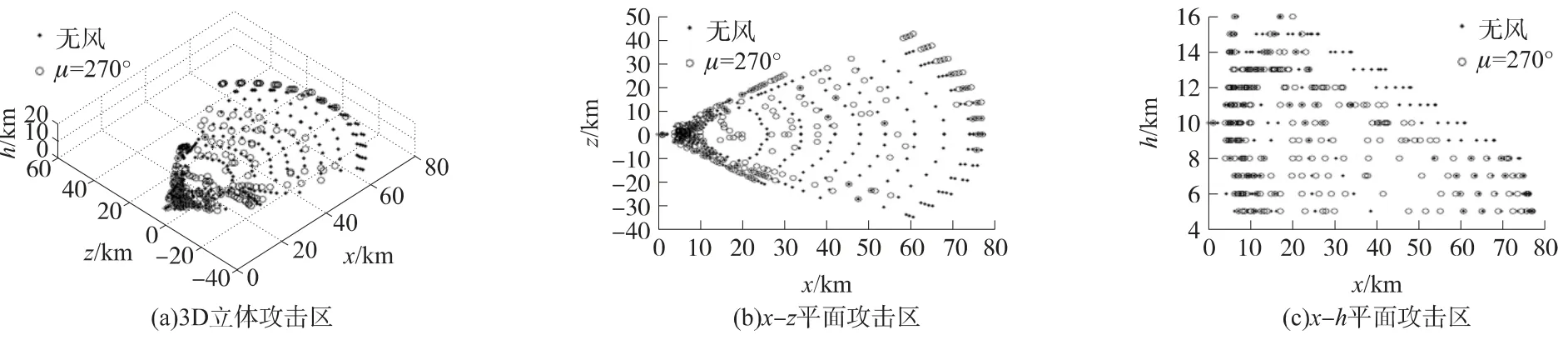
图9 无风与μ＝270°可攻击区的比较

在计算导弹可攻击区随风速方向μ变化时，导弹的飞行高度是导弹从发射点至命中目标点的飞行轨迹的高度，该飞行轨迹的高度随时间的变化过程可以从目标飞行特性及导弹可攻击区（图6（c）～图9（c））中看出.在飞行区域内，不同高度的风速是不同的，可参见图3.风向μ为0°，180°，90°，270°时，风场对空空导弹3D可攻击区的影响如下：

①μ为0°和180°时，从图5～图7中可以看出，μ为0°时的（即导弹顺风飞行）可攻击区与无风可攻击区相比，远边界增大，最远边界点距离增大6km（即7.79%）；近边界基本不变；侧边界减小，最大偏移点距离减小1km.μ为180°时的可攻击区（即导弹逆风飞行）与无风可攻击区相比，远边界减小，最远边界点距离减小5km（即6.49%）；近边界基本不变；侧边界增大，最大偏移点距离增大1.279km.即顺风或逆风干扰时，可攻击区的形状在远边界上发生了明显的变化.

②μ为90°和270°时，从图5、图8与图9中可以看出，μ为90°时（即左侧风干扰时）的攻击区与无风攻击区相比，最远和最近边界点基本不变；侧边界的左侧明显减小，最大偏移点距离减小7.549 6km（即21.55%），侧边界的右侧明显增大，最大偏移点距离增大7.443km（即21.25%）.μ为270°时（即右侧风干扰时）的攻击区与无风攻击区相比，最远和最近边界点基本不变；侧边界的右侧明显减小，最大偏移点距离减小7.505 5km（即21.43%），侧边界的左侧明显增大，最大偏移点距离增大7.388 2km（即21.09%）.即侧风干扰时，可攻击区在侧边界上发生了明显的变化.

由以上分析可知，风场改变了空空导弹可攻击区的大小和形状.

3.2 风场对空空导弹可攻击区敏感度分析

从图5可以看出，当μ从0°到360°变化时，风场对空空导弹可攻击区的相应变化，即敏感度.

①当μ从0°到90°变化时，εμ＜0，则Rmax随μ变化呈非线性减小；ημ≈0，则Rmin基本不变；ξμ＜0，则Lmax朝左侧方向随μ变化呈非线性减小；ζμ＜0，则Dmax朝右侧方向随μ变化呈非线性增大.

②当μ从90°到180°变化时，εμ＜0，则Rmax随μ变化呈非线性减小；ημ≈0，则Rmin基本不变；ξμ＞0，则Lmax朝左侧方向随μ变化呈非线性增大；ζμ＞0，则Dmax朝右侧方向随μ变化呈非线性减小.

③当μ从180°到270°变化时，εμ＞0，则Rmax随μ变化呈非线性增大；ημ≈0，则Rmin基本不变；ξμ＞0，则Lmax朝左侧方向随μ变化呈非线性增大；ζμ＞0，则Dmax朝右侧方向随μ变化呈非线性减小.

④当μ从270°到360°变化时，εμ＞0，则Rmax随μ变化呈非线性增大；ημ≈0，则Rmin基本不变；ξμ＜0，则Lmax朝左侧方向随μ变化呈非线性减小；ζμ＜0，则Dmax朝右侧方向随μ变化呈非线性增大.

综合以上分析表明，在不同风场中，攻击区的形状和大小变化与无风场相比，是随着风向μ呈非线性变化的；若知道空空导弹可攻击区边界的敏感度εμ，ημ，ξμ，ζμ的正负与大小，便可知道空空导弹可攻击区边界的变化趋势与变化率.

3.3 升阻比误差对空空导弹3D可攻击区的影响

导弹可攻击区敏感度随升阻比误差Δλ的变化见图10，升阻比误差Δλ对空空导弹3D可攻击区的影响可以见图11～图14.

图10 敏感度随升阻比误差Δλ变化曲线

图11 Δλ＝0与Δλ＝－30%可攻击区的比较

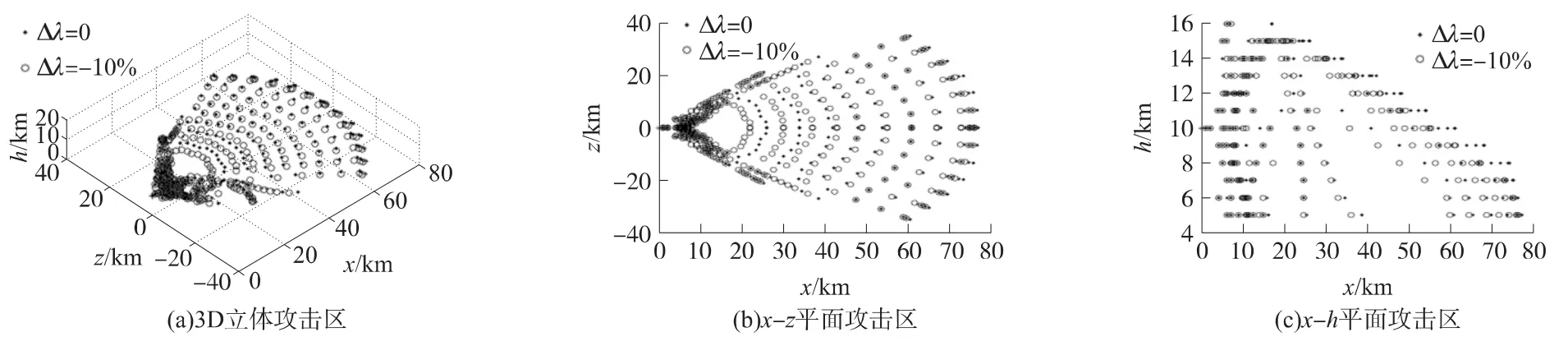
图12 Δλ＝0与Δλ＝－10%可攻击区的比较

图13 Δλ＝0与Δλ＝10%可攻击区的比较

图14 Δλ＝0与Δλ＝30%可攻击区的比较

从图10～图14中可以看出：

①Δλ为－30%时可攻击区与Δλ为0时的可攻击区相比，远边界减小，最远边界点距离减小10km（即12.99%）；近边界基本不变；左右两侧对称，且边界均减小，最大偏移点减小6.004 4km（即17.14%）.

②Δλ为－10%时可攻击区与Δλ为0时的可攻击区相比，远边界减小，最远边界点距离减小1km（即1.3%）；近边界基本不变；左右两侧对称，且边界均减小，最大偏移点减小0.500 4km（即1.43%）.

③Δλ为10%时可攻击区与Δλ为0时的可攻击区相比，远边界增大，最远边界点增大1km（即1.3%）；近边界基本不变；左右两侧对称，且边界均增大，最大偏移点增大0.500 4km（即1.43%）.

④Δλ为30%时可攻击区与Δλ为0时的可攻击区相比，远边界增大，最远边界点增大3km（即3.9%）；近边界基本不变；左右两侧对称，且边界均增大，最大偏移点增大1.501 1km（即4.29%）.

由以上分析可知，升阻比误差改变了可攻击区的形状和大小，且可攻击区对升阻比减小的敏感性比升阻比增大的敏感性强.

3.4 升阻比误差对空空导弹可攻击区敏感度分析

为了使空空导弹可攻击区受升阻比误差影响的结论具有广泛的正确性与适应性，本文研究了范围比较大的升阻比误差对空空导弹可攻击区的影响.Δλ从－30%到30%，ελ＞0，则Rmax随着 Δλ的增大呈非线性增大，ελ越大，Rmax随之增加幅度越大；ηλ≈0，则Rmin基本不变；ξλ＞0，则Lmax随 Δλ朝左侧方向呈非线性增大，ξλ越大，Lmax随之增加幅度越大；ζλ＜0，则Dmax随Δλ朝右侧方向呈非线性增大，ζλ越小，则Dmax随之增加幅度越大.因此，可攻击区的形状和大小随着升阻比误差Δλ的增大呈非线性扩展，并且若知道空空导弹可攻击区边界的敏感度ελ、ηλ、ξλ、ζλ的正负与大小，便可知道空空导弹可攻击区边界的变化趋势与变化率.

4 结束语

本文深入研究了空空导弹的可攻击区对风场干扰和升阻比误差的敏感度，主要结论如下：①空空导弹可攻击区的形状和大小随着风速方向变化或随升阻比误差变化，且呈非线性变化.②通过计算空空导弹可攻击区边界敏感度的正负与数值大小，便可判断空空导弹可攻击区边界的变化趋势与变化率.③对于可攻击区近边界，导弹发动机处于工作状态，风场干扰和升阻比误差对空空导弹飞行影响很小，因此空空导弹近边界基本不变；对于可攻击区的远边界和侧边界，导弹发动机早已停机，空空导弹做滑翔飞行，容易受风场干扰和升阻比误差的影响，因此空空导弹远边界和侧边界变化明显.④虽然本文只大量数值仿真计算了空空导弹和目标迎击时的情况，但其它全部的各种导弹和目标相对运动的情况出现时，则可攻击区对风场干扰和升阻比误差也具有相应的敏感度.

因此，当计算空空导弹的可攻击区时，风场干扰和升阻比误差是必须考虑的，这具有实际工程设计与空战应用价值.

[1]张安.空空导弹发射包线灵敏度分析研究[J].西北工业大学学报，1994，12（4）：567－571.ZHANG An.On sensitivity analysis of launch envelope of Chinese air－to－air missile[J].Journal of Northwestern Poly－technical University，1994，12（4）：567－571.（in Chinese）

[2]王志刚，陈士橹，胡小君.飞机敏捷性与空空导弹攻击区综合研究[J].飞行力学，1998，16（4）：1－6.WANG Zhi－gang，CHEN Shi－lu，HU Xiao－jun.Study of fighter agility and the air－to－air missile’s attack region[J].Flight Dynamics，1998，16（4）：1－6.（in Chinese）

[3]廖俊.某型推力矢量控制空空导弹攻击区仿真研究[J].弹箭与制导学报，2006，26（4）：43－45.LIAO Jun.Research on the attack zone simulation of a kind of air－to－air missile with thrust vector control[J].Arrow and Guidance Journal，2006，26（4）：43－45.（in Chinese）

[4]鞠传文，史玮韦.半主动雷达寻的空空导弹作战技术运用研究[J].航空计算技术，2009，39（1）：71－74.JU Chuan－wen，SHI Wei－wei.Study on half－active radar air－toair missiles use in air fight[J].Aviation Computing Technology，2009，39（1）：71－74.（in Chinese）

[5]张安，刘岗.空空导弹不可逃逸区仿真研究[J].航空兵器，2000，（2）：8－10.ZHANG An，LIU Gang.Research on no－escape of attack zone simulation of air－to－air missile[J].Aviation Weapon，2000，（2）：8－10.（in Chinese）

[6]黄国强，南英，陆宇平.空空导弹擦肩发射全向三维可攻击区计算[J].弹道学报，2011，23（2）：37－38.HUANG Guo－qiang，NAN Ying，LU Yu－ping.Calculation of all－aspect attack zone for air－to－air missile merge[J].Journal of Ballistics，2011，23（2）：37－38.（in Chinese）

[7]LINDZEN R S.Turbulence and stress owing to gravity wave and tidal breakdown[J].Journal of Geophysical Research，1981，86（C10）：9 707－9 714.

[8]YU Yong－hui.A numerical model characterizing internal gravity wave propagation into the upper atmosphere[J].Advances in Space Research，2009，44（7）：836－846.