空投雷弹斜入水初始弹道数值分析
王永虎,石秀华
(1.中国民航飞行学院,四川 广汉618307;2.西北工业大学 航海学院,西安710072)
自从上世纪20年代末水上飞机的水面降落问题提出以来,结构物入水冲击的理论与试验研究得到了飞速发展,例如,水上飞机和宇宙飞船水面着陆、卫星海面回收、空投雷弹入水冲击、船舶在风浪中砰击和救生艇的海上抛落等[1,2].由于理论分析入水初始弹道比较困难,忽扑行为的研究也只局限于定性分析,所以入水初始弹道和忽扑在空投雷弹入水冲击问题中的研究就显得尤为重要.20世纪60年代,WAUGH J G在假雷和实雷实验基础上,对空投雷弹入水弹道和忽扑行为进行了研究[2,3].为了研究空投水雷的入水以及水下运动行为机理,达到更准确地布雷,MANN J L采用蒙特卡罗法获得三维水雷模型 MINE6D的运动轨迹[4].CHU P C等建立时域3DOF运动方程以及回归模型,对圆柱体跌落入水进行了理论分析和实验研究[5,6].PARK Man-sung等[7]利用面元法数值计算了正切尖拱体以任意角度入水的冲击载荷,然后对尖拱体的忽扑行为进行了数值计算分析,但是在数值计算中忽略了入水空泡对入水弹道的影响,计算结果不可避免地存在误差.由于空投雷弹斜入水的复杂性和特殊性,必须对其入水初始弹道进行准确分析以确保斜入水的航行安全性.
1 入水冲击显式动力模型
用数理解析方法和数值方法研究入水初始弹道问题时,必须把结构动力学方程和流体动力学方程耦合起来求解,解析方法只适应于简化模型,而数值模拟应用范围更广.LS-DYNA是以显式为主、隐式为辅的非线性动力有限元仿真软件,程序中的单元采用拉格朗日列式增量解法,特别适合求解各种二维、三维非线性动力冲击问题,并与实验进行无数次的对比,证实了模拟计算的可靠性[8].下面首先根据多物质流固耦合方法,建立斜入水冲击显式动力模型;然后数值模拟入水冲击过程,最后应用到入水初始弹道问题的研究中.
1.1 固体域网格划分
在入水冲击的显式动力模型中,采用有限元方法离散入水结构体(固体域),其有限元方程为

式中,M为总质量矩阵;C为结构阻尼系数;P为总体载荷矢量;F为单元应力场等效节点力矢量组;H为总体结构沙漏粘性阻尼力(t)为总体节点加速度矢量(t)为总体节点速度矢量.
为了真实模拟入水冲击的液面隆起现象,并提高数值计算速度,求解算法上采用LS-DYNA程序中的多物质ALE算法.由于无反射边界只能施加到实体单元上,入水结构体采用LS-DYNA单元库中的六面体SOLID164体元模拟.为了与水域、空气域耦合,固体域的网格划分采用Lagrange网格算法.如果结构体外形特殊(例如尖拱体),需采用布尔运算划分网格,对尖拱体进行了八节点体元网格划分.同时,为了节省计时,采用沙漏粘性阻尼方式控制单点积分引起沙漏模式,这对模拟液面隆起和飞溅等大变形现象十分有效.由于只讨论入水初始弹道,所以将空投雷弹结构外形简化为图1所示的数值模型.
在数值计算过程中,采用LS-DYNA的中心差分时间积分的显式方法,计算系统各节点在第n时间步时刻的加速度a、速度v和位移s分别为

式中,Fext为节点外力和体力矩阵,Fint为节点内力矩阵.


图1 空投雷弹斜入水冲击数值模型及计算域
1.2 流体域网格划分
空投雷弹入水冲击涉及到三相介质:固体域、空气域和水域.空气域和水域均采用LS-DYNA中的空材料模式*MAT_NULL来描述,即用本构模型和状态方程来同时描述流体材料,通过Gruneisen状态方程确定压力-体积的关系式:

式中,ρ0为材料密度;vc为冲击波速度;E0为单位体积内能;S1、S2、S3、γ0为材料常数;μ为密度变化率;α为一阶体积修正.在LS-DYNA中采用*EOS_GUNEISEN关键字定义,其中水和空气2种流体采用Euler网格建模,建模时水和空气介质均使用映射方法划分网格.流体材料本构模型和状态方程具体参数分别见表1,本文数值模型采用cm-g-μs单位制,流体材料本构模型和状态方程具体参数分别见表1.
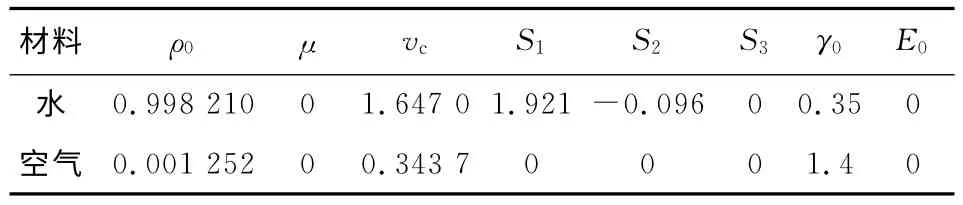
表1 流体材料的本构模型和状态方程的相关参数
1.3 流固耦合ALE算法
本文采用ALE算法,结合Euler算法与Lagrange算法的优点,结构采用Lagrange单元算法,流体采用Euler/ALE多物质单元算法.ALE算法先执行一个或几个Lagrange时步计算,单元网格随材料流动而产生变形.然后,为了保持变形后的物质边界条件,对内部单元重新划分网格,将变形网格中的单元变量(密度、能量、应力张量等)和接点速度矢量输运到重分后的新网格中,最后执行ALE时步计算.特点是耦合面随着Lagrange单元和Euler单元形成的共同边界产生运动变形,Euler单元也就可以随着结构大范围移动,保证了数值计算顺利进行,且大大节约计时.
LS-DYNA程序中的多物质ALE-Lagrange算法可以传递ALE网格中的流体材料和Lagrange结构体间的接触力,能方便地通过*CONSTRAINED_LAGRANGE_IN_SOLID关键字把流体和固体单元进行耦合,且建模时流体网格和固体网格可以交叉重叠.通过*SECTION_SOILD_ALE关键字来定义单元算法类型并标识相关单元算法.为了更接近模拟无限水域的分析情况,在流体单元的边界上定义无反射边界条件来简化入水冲击模型.
1.4 网格划分尺寸控制
流体网格密度对数值结果是有影响的,理论上讲网格划分越细,数值计算结果越接近真实值,但实际中细密的网格划分会造成数值计算中误差累积、结果偏离和计时延长.考虑到计算机允许的计算能力和工程应用的精度要求,合理确定网格密度和计算规模是非常必要的.
为了确定最佳的网格密度,并捕捉应力场的最大梯度变化,这里采用一个无量纲参量来描述网格密度,定义Euler-Lagrange单元网格尺寸比为

式中,LEu为Euler单元网格特征尺寸;LLag为Lagrange单元网格特征尺寸.一般而言,尺寸比的选取以在仿真过程中数值收敛性好,计算结果较精确为准.这里对Rm=0.4~0.9的情况进行了数值计算,计算结果见图2,图中Cd为入水冲击阻力系数.
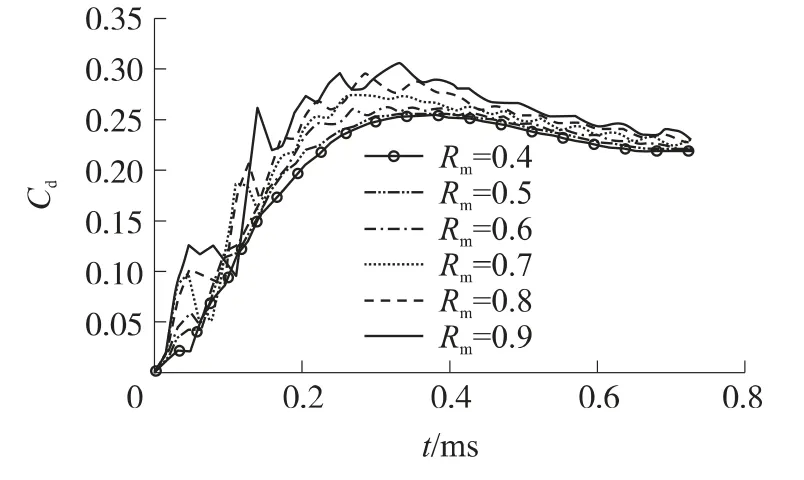
图2 不同Rm的计算精度曲线
由图2可以看出,随着尺寸比的减少,曲线震荡明显减弱,而且入水冲击载荷峰值也在减少,当Rm=0.6时曲线趋于平稳,当Rm=0.4时得到最稳定的曲线.数值计算效益和经济性不仅要考虑结果的精确度,而且要看计算消耗的机时和存取容量.虽然Rm=0.4的结果较精确,但计时较长和存储容量骤然增大.因此,这里在空投雷弹入水冲击数值计算中,Rm取0.5~0.6较合理,故本文后续的弹道分析均采用Rm=0.6.
2 计算结果与分析
为了便于模型的建立和高效的数值求解,这里主要分析空投雷弹二维入水运动学行为,即入水初始弹道,将结构体定义为刚性体以减少自由度的数量,每次数值仿真的固体域的尺寸和网格划分方法都不变.为了保证入水弹道轨迹和射流飞溅大部分出现在流体域中,根据入水初始弹道时间和水平距离确定流体域尺寸,这样会导致每次数值计算中网格数量不一致,但不影响数值仿真结果的准确性.
尖拱体斜入水的初始条件和物理参数为:根据空投雷弹的实际质量,设定尖拱体质量为18.4kg,局部坐标系中质心的转动惯量在K文件中设定为*DIM,Ivert,ARRAY,6,1,1,,,、*SET,IVERT(1,1,1),5189233、*SET,IVERT (4,1,1),2312606、*SET,IVERT(6,1,1),5189233,单位为cm-g-μs.数值计算得到各情况下的入水初始弹道,并通过二维图来表示.
首先,为了研究入水角对忽扑行为的影响,在初始入水速度为100m/s,初始攻角为0,对入水角分别以10°、20°和30°的初始弹道进行模拟.采用尖拱顶点运动轨迹来形象显示水下初始弹道,见图3所示.可以看出,入水角越小,运动轨迹越偏离初始轨道;也表明入水角越小,尖拱体越容易产生忽扑行为甚至弹跳,与文献[7]采用面元法的数值结果吻合,究其原因是入水角小的尖拱体在入水过程中受到的纵倾力矩大.
然后,对质量为18.4kg尖拱体以固定的30°入水角且零攻角情况下的斜入水进行数值仿真,选择入 水 初 速 度v0分 别 为 30.48 m/s,60 m/s 和100m/s,分析初始速度对入水初始弹道的影响,见图4所示,图中显示的是二维Oxy坐标系中顶点运动轨迹.可以看出,虽然入水速度不同,但只要攻角和入水角不变,尖拱顶点的运动轨迹是相同的,即入水角对入水初始弹道的影响微乎其微.图5给出了不同质量的尖拱体在v0=100m/s和相同时间情况下的入水初始弹道二维图,可以看出,随着入水体质量的增加,在相同时间内,质量小的尖拱体入水初始弹道曲率较大,从而很容易产生忽扑或弹跳行为.

图3 以相应入水角入水的初始弹道
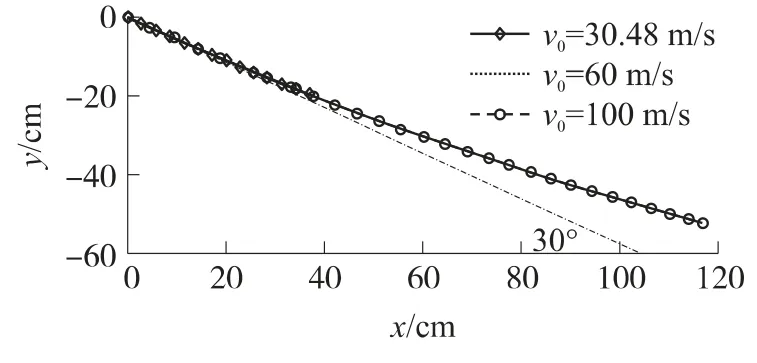
图4 入水速度不同的入水初始弹道

图5 质量不同的入水初始弹道
最后,空投雷弹与流体刚刚接触的时候具有一定的入水攻角,这里数值分析了初始攻角对入水运动初始轨迹的影响,见图6所示.分别选取了3种情况进行模拟仿真,即入水攻角α0分别为-5°、0°和5°,入水初始速度为100m/s,入水角为固定的30°.
从仿真结果可以看出,在入水初速度和入水角速度一定的条件下,入水初始攻角对入水初始运动轨迹和姿态角变化影响较大.正攻角入水使雷弹往拉平方向运动,加剧忽扑甚至出现弹跳行为;负攻角入水使雷弹具有俯冲下潜的趋势,起到抑制的作用.所以,在小角度斜入水过程中应注意入水攻角的影响作用.
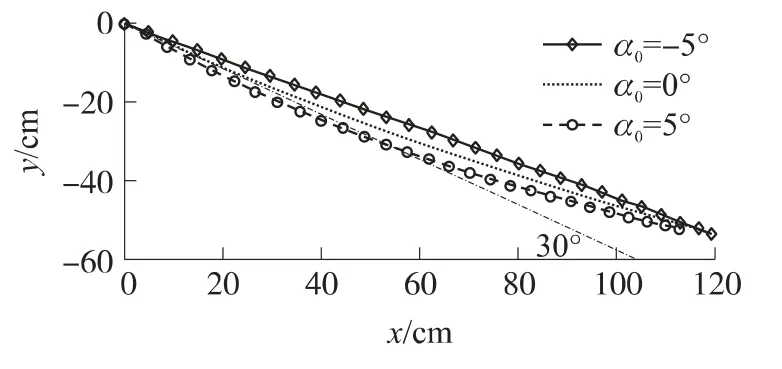
图6 初始攻角不同的水下初始弹道
3 结论
采用ANSYS/LS-DYNA大型非线性显式动力程序进行空投雷弹斜入水初始弹道模拟研究,实现入水空泡生成和扩展现象以及不正常入水造成的忽扑行为模拟,考虑了初始条件和物理条件对斜入水初始弹道的影响,得到以下结论:①入水角对入水初始弹道影响很大,如果入水角很小可能产生忽扑行为甚至弹跳行为,这对空投雷弹而言是不利的影响因素;②入水初速度对入水初始弹道几乎没有什么影响,空投雷弹都是沿着近似相同的弹道运行;③空投雷弹自身的质量对入水初始弹道也有影响,在其他条件相同的条件下质量越小越容易产生忽扑行为;④对带有攻角姿态而言,攻角大小对初始弹道有不同的影响,特别针对小角度斜入水情况,可以考虑采用适当攻角来弥补小角度带来的负面影响,此入水初始弹道规律将指导后续的入水弹道定性或定量分析.
[1]WANG Y,SHI X,WANG P.Dynamical response analysis of incautious water entry of UUV based on exact body shape approach[C].7th World Congress on Intelligent Control and Automation.Chongqing,China:IEEE,2008:4 870-4 875.
[2]WAUGH J G.Water-entry pitch modeling[J].Journal of Hydronautics,1968,2(2):87-92.
[3]WAUGH J G,STUBSTAD G W.Hydroballistics modeling,AD A007529[R].1975.
[4]MANN J L.Deterministic and stochastic modeling of the water entry and descent of three-dimensional cylinderical bodies[D].USA:Massachusetts Institute of Technology,2005.
[5]CHU P C,FAN C W.3Drigid body impact burial prediction model[J].Advances in Mechanics,2004,5:43-52.
[6]CHU P C,FAN C W.Pseudo-cylinder parameterization for mine impact burial prediction[J].Journal of Fluids Engineering,2005,127:1 515-1 520.
[7]PARK Man-sung,JUNG Young-rae.Numerical study of impact force and ricochet behavior of high speed water-entry bodies[J].Computers & Fluids,2003,32:939-951.
[8]HALLQUIST J O.LS-DYNA theoretical manual[M].Livermore,California:Livermore Software Technology Corporation,2006.

