一种控制多弹协同攻击时间和攻击角度的方法
王晓芳,洪 鑫,林 海
(北京理工大学 宇航学院,北京100081)
随着科学技术的高速发展,导弹防御系统的能力不断增强,单枚导弹作战在很多情况下已无法满足战场的要求,多枚导弹协同作战变得越来越重要.为了提高导弹协同作战的杀伤力,通常对攻击角度有要求,而为了实现饱和攻击,又对攻击时间有要求.文献[1~3]分别基于最优控制理论和比例导引律设计了控制导弹攻击角度的制导律;文献[4,5]对具有攻击时间约束的制导律进行了研究;文献[6]基于最优控制理论提出了一种可同时控制多枚导弹攻击方位角和攻击时间的二维制导律;文献[7,8]中提出了同时具有攻击角度和攻击时间约束的三维制导律,但两种制导律都需要预先设定理想攻击时间,而理想攻击时间的合理设定一直是一个难点.
本文提出一种对多枚导弹的攻击角度和攻击时间进行控制的基于虚拟球体的方法.选其中一枚导弹作为领弹,以目标为球心、领弹与目标之间的距离为半径构造虚拟球体,针对剩余的每枚导弹(称作从弹)设计对应在虚拟球体表面的虚拟点:虚拟点和目标连线的方向为此从弹的理想攻击角方向.领弹采用比例导引律,虚拟球体随着领弹的飞行逐渐缩小至目标点,设计最优控制器控制从弹逼近和跟踪虚拟点,从而实现多枚导弹从不同的角度同时命中目标.为了减小从弹对虚拟点逼近和跟踪时的需用过载,基于以上思路,对虚拟点轨迹进行了改进设计.
1 攻击角度和攻击时间控制模型
多枚导弹协同攻击目标时,选择其中一枚为领弹.在以目标为球心、领弹距目标的距离为半径的虚拟球体上,根据某从弹的理想攻击角确定它此时对应的虚拟点,如图1所示.图1中,Axyz为地面坐标系,Ml(xl,yl,zl)、Mfi(xfi,yfi,zfi)、Mvi(xvi,yvi,zvi)和T(xt,yt,zt)分别为领弹、第i枚从弹和它对应的虚拟点、目标及它们在地面坐标系中的位置.rl为领弹与目标之间的距离.εyi和εzi为第i枚从弹在俯仰方向和偏航方向的理想攻击角.Mvixviyvizvi为虚拟点坐标系,它的原点为虚拟点Mvi,Mvixvi轴与虚拟点和目标的连线重合,指向目标为正;Mviyvi轴位于包含Mvixvi轴的铅垂面内垂直于Mvixvi轴,指向上为正;Mvizvi轴与其它两轴构成右手直角坐标系.

图1 领弹、从弹与虚拟点的相对位置图
在对协同作战的导弹进行攻击角度和攻击时间控制的研究中,假设从弹的控制系统是闭环稳定的,即可以实现对从弹速度指令vfc,弹道倾角指令θfc以及弹道偏角指令ψVfc的稳定跟随控制.设这3个通道可以简化为参考文献[9]中所示的一阶系统,为了节省篇幅,这里不再列出.本文中vf、θf和ψVf亦指从弹的速度、弹道倾角和弹道偏角.
本文中控制方法的设计思路:首先,以目标为球心,领弹相对于目标的距离为半径构造一虚拟球体,然后根据某从弹的理想攻击角确定其在虚拟球体上的一个虚拟点,最后设计最优控制器控制从弹逼近并跟踪此虚拟点.当领弹按照比例导引律攻击目标时,所构造的虚拟球体将随领弹与目标的距离变短而逐渐缩小,虚拟球体上的虚拟点从理想攻击角方向以直线逼近目标,控制器控制从弹跟踪虚拟点运动,最后以理想攻击角和领弹同时到达目标.根据图1可知,在已知目标位置的基础上,虚拟点在地面坐标系中的位置可表示为(省去下标i)

本文中的理想攻击角εy、εz为常数,那么,对式(1)求导可得到:

式中,目标位置、εy、εz已知,由于领弹运动状态已知,因此l也可计算得到,则在导弹飞行过程中,根据式(2)可得到每一时刻的v、v和v.
表征从弹运动的方程组为

从弹与其对应的虚拟点在地面坐标系中的位置差为

将从弹与虚拟点在地面坐标系中的位置差转换到虚拟点坐标系中有:

式中,L(εy)、L(εz)为初等旋转矩阵,其值可见文献[10].将式(4)代入式(5)展开、化简并求导可得:
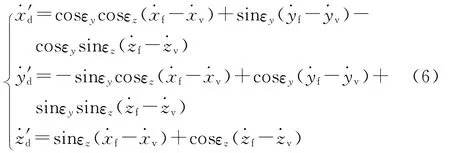
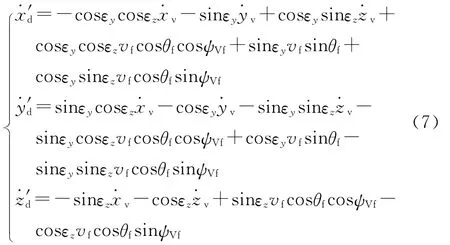
为了简化式(7)的表达形式,可令:
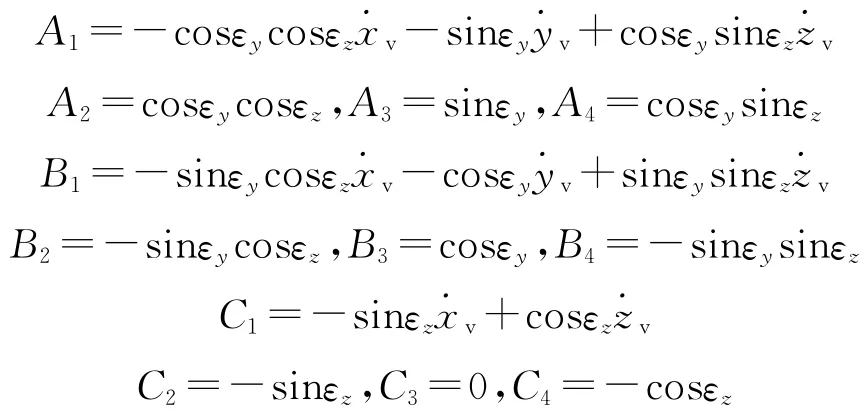
由于εy、εz、v、v和v均为已知,因此Ai、Bi、Ci(i=1,2,3,4)为已知.式(7)变为
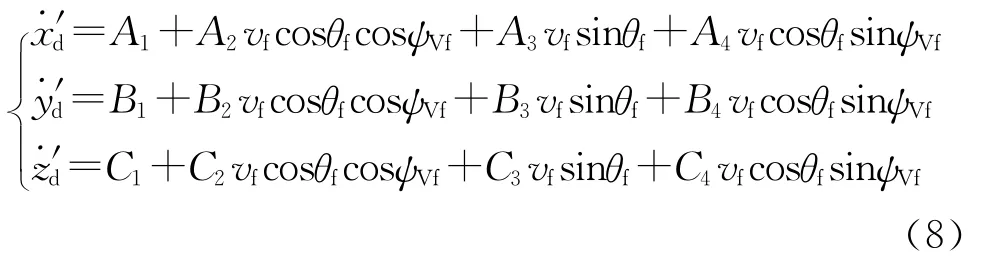
在控制攻击角度和攻击时间的控制器中,控制变量为从弹的运动参数vf、θf和ψVf.从式(8)可知,此时的系统为非线性控制系统,可通过变量代换的方法使其可采用线性系统的方法进行求解.令u1=vfcosθfcosψVf,u2=vfsinθf,u3=vfcosθfsinψVf,则式(8)变为

将式(9)写成状态方程,形式为

式中,状态变量X=(x′dy′dz′d)T,控制变量U=(u1u2u3)T,扰动量W=(A1B1C1)T,系统矩阵A为零矩阵,控制矩阵B为

对系统进行控制的目的是使从弹与虚拟点重合并跟踪虚拟点,也就是使X为0.在求得控制变量U后,通过变换得到从弹的运动参数指令vfc、θfc和ψVfc,变换公式为

运动参数指令经过从弹的一阶稳定控制系统,得到从弹的真实飞行参数vf、θf和ψVf.
2 虚拟点轨迹的改进
理想的虚拟点轨迹是一条直线,直接控制从弹逼近这条直线,对从弹的需用过载提出较高的要求.如对虚拟点轨迹进行改进,使它的前段变为曲线,逐步过渡交汇到原来设计的直线上,然后控制从弹逼近这条“曲线+直线”的轨迹,则会显著降低对从弹需用过载的要求.假设当前从弹距目标的距离为rf,从弹与目标之间的视线角为εyf和εzf.把虚拟点和从弹到目标的距离之差Δr=rl-rf、理想攻击角和实际视线角之差Δεy=εy-εyf、Δεz=εz-εzf分为N份,设计虚拟点分N步逐渐靠近理想虚拟点,N步以后和理想虚拟点重合.这时,虚拟点在地面坐标系的位置由式(1)变为

式中,整数n=1,2,…N.领弹的攻击时间t*可根据文献[7]中的算法预估得到,假设仿真步长为h,则N可根据以下式子取值:

式中,系数k≤1.k越大,实际虚拟点轨迹交汇到理想虚拟点轨迹上的时间越晚,对降低导弹的需用过载要求越有利.
3 最优控制器的设计
对式(10)所示的模型进行变换,令W′=B-1W,则式(10)可变为

令U1=U+W′,则有:=AX+BU1.
采用最优控制原理对式(14)所示问题进行求解.由于控制的目的是使状态X为0,因此可把其看作一个状态调节器问题.控制器的性能指标采用如下所示的线性二次性能指标:
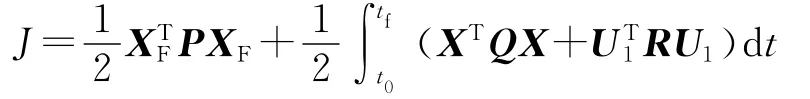
式中,P、Q为对称半正定阵,R为对称正定阵,为了计算的方便,它们通常取对角常数阵.XF为终点时的状态,本问题中它为0.这时,线性二次性能指标变为

系统的初始条件为开始时从弹与虚拟点的位置差,可由式(4)计算得到.根据最优控制理论可得到最优控制量的解为U1=-R-1BTKX.式中,K为最优控制黎卡提方程的解.再作变换得到式(10)所示系统的控制变量为U=U1-W′.得到U之后根据式(11)便得到从弹的运动参数指令.
4 仿真分析
假设领弹和3枚从弹协同攻击一个直线运动舰艇.目标的初始位置为(6000m,0,3 000m),速度为18m/s,航向角为45°.4枚导弹均由平飞状态转入末制导,因此,初始弹道倾角均设为0,考虑导弹在偏航方向受到中制导的作用,设转入末制导时导弹的弹道偏角与视线角相差不大,4枚导弹的初始参数如表1所示.从弹控制系统中速度、弹道倾角、弹道偏角3个控制通道的时间常数分别为3s、1s、1s.控制器的权系数矩阵为Q=diag(1,1,1),R=diag(0.5,0.5,0.5).考虑到导弹的能量限制,对从弹的飞行状态进行限幅,即|vf-vf0|≤60 m/s,|θf-θf0|≤15°,|ψVf-ψVf0|≤30°,其中带下标“0”的量表示初始值.

表1 导弹的初始参数
领弹在俯仰方向和偏航方向均采用比例系数为3的比例导引律,从弹采用所设计的最优控制器,仿真结果如图2~图5所示.3枚从弹的理想攻击角和实际攻击角以及攻击时间如表2所示,t*为攻击时间,εys、εzs为导弹(包括领弹和从弹)的实际攻击角,对于从弹来讲,εys=εyf,εzs=εzf.
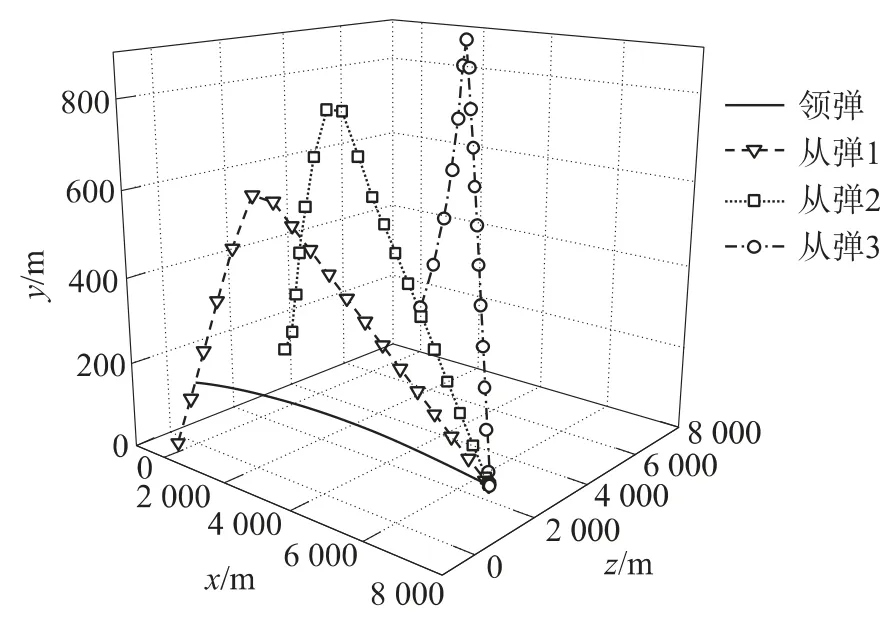
图2 导弹三维弹道图
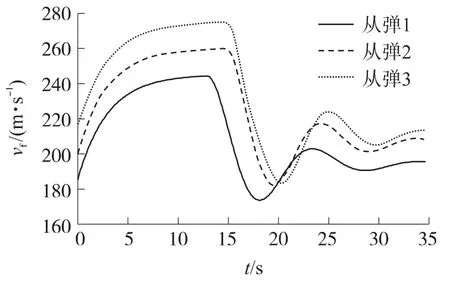
图3 从弹速度变化图
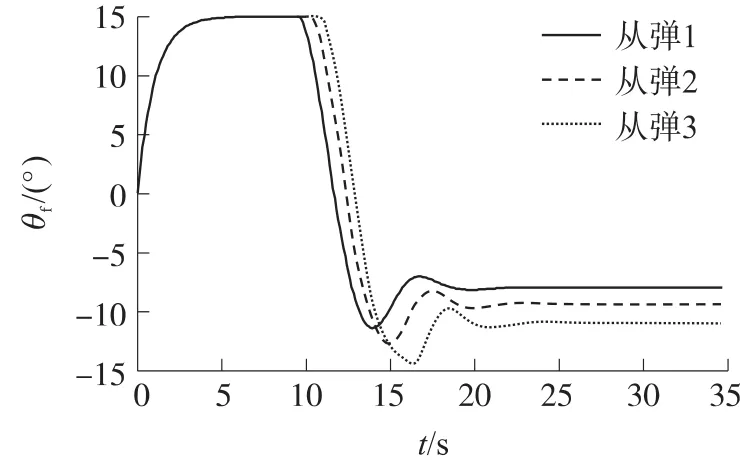
图4 从弹弹道倾角变化图

图5 从弹弹道偏角变化图
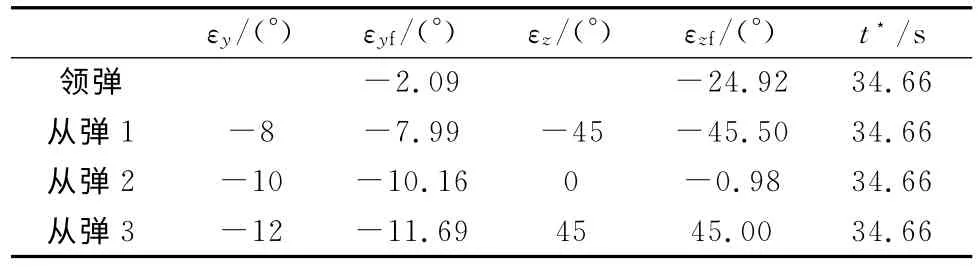
表2 导弹的攻击角度和攻击时间
对仿真结果进行分析可知:
①在飞行时间为34.66s时,领弹与3枚从弹距目标的距离均小于2m,可认为4枚导弹同时命中了目标.4枚导弹协同作战的攻击时间由领弹的飞行时间确定,并不需要提前指定,因此,本文中的方法在实际应用时比较方便.
②3枚从弹在俯仰方向和偏航方向的实际攻击角与理想攻击角相差不大,最大偏差不超过1°.本文中,领弹采用比例导引律飞行,并没有对它的攻击角度进行控制.但由于领弹在以比例导引律飞行,可以估算出它的攻击角度,这个攻击角度作为其它几枚从弹理想攻击角度设定的参考.通过设定不同的理想攻击角来实现领弹和从弹从不同的方向命中目标,得到良好的作战效果.在实际应用时,领弹也可以采用带有落角约束的任何一种制导律来对它的攻击角度进行控制,这并不影响本文所提方法的使用.本文的领弹之所以采用比例导引律,是出于对导弹命中精度和协同作战时高低弹道综合应用的考虑.
③由于从弹1、从弹2和从弹3的初始视线角和速度矢量方向与理想攻击角偏差较大,因此,3个从弹控制器开始时输出的速度、弹道倾角和弹道偏角比较大,均被限幅.从弹3的初始弹目距离与领弹的初始弹目距离之差、竖直方向的初始视线角与理想攻击角之差比从弹1和从弹2大,因此,控制器输出的速度和弹道倾角受到限幅的时间最长.而在偏航方向,从弹3的初始视线角与理想攻击角之差最小,因此,从弹3控制器输出的弹道偏角受限幅时间最短,最先达到稳态.图3~图5中的曲线是控制指令经过从弹一阶惯性控制系统后的从弹实际运动状态随时间变化的曲线,上述结论可从图3~图5中看出.由以上分析可知,从弹的初始状态对控制器的输出有较大的影响.
④通过调节控制器的权系数矩阵Q和R可以减小控制的稳态误差,但同时会影响控制量及其变化率,因此需要合理设置控制器的权系数矩阵,使稳态误差和控制量都在允许的范围内.
采用如式(12)所示的方法对虚拟点轨迹进行改进设计,N按照式(13)取值,本算例中取k=1.以从弹2为例,理想虚拟点轨迹、实际虚拟点轨迹以及从弹2的弹道如图6所示.改进前后的从弹2的法向过载随时间的变化如图7、图8所示,图中nyf和nzf分别为从弹2在铅垂平面和水平面内的法向过载.
由图中可见,改进后的虚拟点轨迹先是一段曲线,此曲线逐渐逼近理想虚拟点的直线轨迹,最后和理想虚拟点轨迹重合,从弹趋近并跟踪改进后的虚拟点轨迹,最后实现了对攻击角度和攻击时间的控制.虚拟点轨迹改进后,导弹的需用过载也大大减小.
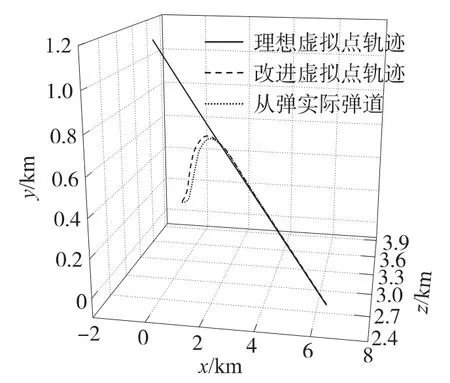
图6 虚拟点轨迹及从弹2弹道图

图7 从弹2在铅垂平面内的法向过载变化图

图8 从弹2在水平面内的法向过载变化图
5 结束语
针对多枚导弹协同攻击目标的情况,本文提出了一种控制从弹跟踪位于逐渐缩小的虚拟球体上的虚拟点,从而实现导弹攻击时间和攻击角度协同的方法.本方法具有无需事先指定理想攻击时间、可攻击的目标运动状态不受限制、可实现三维空间攻击的优点.另外,还可设计不同的算法对虚拟点轨迹进行改进来减小从弹的需用过载.总之,该方法在应用方面有很大灵活性,具有较广阔的军事应用前景.
[1]SONG T L,SHIN S J,CHO H.Impact angle control for planar engagements[J].IEEE Transactions on Aerospace and Electronic Systems,1999,35(4):1 439-1 444.
[2]RATNOO A,GHOSE D.Impact angle constrained interception of stationary targets[J].Journal of Guidance,Control,and Dynamics,2008,31(6):1 816-1 821.
[3]顾文锦,雷军委,潘长鹏.带落角限制的虚拟目标比例导引律设计[J].飞行力学,2006,24(2):43-46.GU Wen-jin,LEI Jun-wei,PAN Chang-peng.Design of the climbing trajectory using virtual target’s proportional navigation method with the control of terminal azimuth of a missile[J].Flight Dynamics,2006,24(2):43-46.(in Chinese)
[4]JEON I S,LEE J I,TAHK M J.Homing guidance law for cooperative attack of multiple missiles[J].Journal of Guidance,Control,and Dynamics,2010,33(1):275-280.
[5]赵世钰,周锐.基于协调变量的多导弹协同制导[J].航空学报,2008,29(6):1 605-1 611.ZHAO Shi-yu,ZHOU Rui.Multi-missile cooperative guidance using coordination variable[J].Acta Aeronautica et Astronautica Sinica,2008,29(6):1 605-1 611.(in Chinese)
[6]LEE J I,JEON I S,TAHK M J.Guidance law to control impact time and angle[J].IEEE Transactions on Aerospace and Electronic Systems,2007,43(1):301-310.
[7]JUNG B,KIM Y.Guidance law for anti-ship missiles using impact angle and impact time[C].AIAA Guidance,Navigation,and Control Conference and Exhibit.USA:AIAA,2006:1-13.
[8]张友安,马培蓓.带有攻击角度和攻击时间控制的三维制导[J].航空学报,2008,29(4):1 020-1 026.ZHANG You-an,MA Pei-bei.Three-dimensional guidance law with impact angle and impact time constraints[J].Acta Aeronautica et Astronautica Sinica,2008,29(4):1 020-1 026.(in Chinese)
[9]韦常柱,郭继峰,崔乃刚.导弹协同作战编队队形最优保持控制器设计[J].宇航学报,2010,31(4):1 043-1 050.WEI Chang-zhu,GUO Ji-feng,CUI Nai-gang.Research on the missile formation keeping optical control for cooperative engagement[J].Journal of Astronautics,2010,31 (4):1 043 -1 050.(in Chinese)
[10]钱杏芳,林瑞雄,赵亚男.导弹飞行力学[M].北京:北京理工大学出版社,2003.QIAN Xing-fang,LIN Rui-xiong,ZHAO Ya-nan.Missile flight dynamics[M].Beijing:Beijing Institute of Technology Press,2003.

