基于极化特征的旋转弹丸飞行姿态测量方法研究
王元钦,谭久彬,张若禹
(1.哈尔滨工业大学 超精密光电仪器工程研究所,哈尔滨150001;2.中国人民解放军装备学院,北京102249)
弹丸飞行姿态是指弹丸运动过程中弹轴的空间指向.由于火炮弹丸的体积小、速度快、过载高,弹丸飞行姿态测量是武器靶场试验的技术难题.目前,国内外弹丸飞行姿态测量主要有纸靶法[1]、光学法[2]和传感器遥测法[3]等.纸靶法的测量精度较低,且只适应于低伸弹道的测量;光学法测量设备复杂、成本高,测量过程易受气象条件的限制;传感器遥测法虽然能够获得较长弹道范围的弹丸飞行姿态,但在弹丸上安装姿态传感器有较大的难度.由于弹丸飞行姿态是反映弹丸飞行特性的重要参数,武器系统靶场试验需要简单、方便的弹丸飞行姿态测量方法.弹道测速雷达是常规武器靶场的重要测量设备,主要用于弹丸飞行速度的测量.探索利用弹道测速雷达来测量旋转弹丸飞行姿态对武器系统靶场试验测试方法研究具有重要意义.
本文研究利用弹道测速雷达测量旋转弹丸飞行姿态的原理和方法.在分析测速雷达测量旋转弹丸飞行姿态难点的基础上,研究弹丸的雷达散射特性,提出了一种利用弹丸底部刻槽使其产生极化特征,从弹丸雷达回波信号中确定旋转弹丸飞行姿态的方法.通过理论分析和仿真计算证明了方法的可行性.
1 雷达测量弹丸飞行姿态的难点和解决问题的思路
测速雷达的弹丸回波信号r(t)通常可以表示为幅度A、角频率ω和相位φ的函数,即
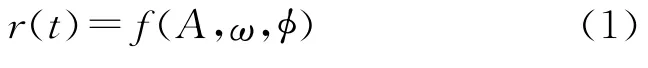
利用雷达测量目标飞行姿态的实质就是从雷达回波r(t)中获得弹丸的飞行姿态α(t)和β(t)(α、β分别为弹轴相对于雷达电轴的俯仰角和方位角).普通弹丸回波信号r(t)与飞行姿态α(t)、β(t)之间没有直接、简单的对应关系,难以从弹丸回波r(t)中直接获得弹丸的飞行姿态.
对于窄带、低分辨率雷达,目标呈现单个散射点特性.雷达回波信号中可以利用的主要特征是多普勒频率、雷达散射截面积(RCS)及其起伏特征,如均值、方差、极大值、极小值等[4].由于目标 RCS的测量受自身形状、噪声和干扰源等因素的影响较大,利用其只能粗略地测量卫星、导弹和火箭等大型目标的姿态[5].相较于这些大型目标小得多的火炮弹丸而言,利用雷达散射截面积难以实现弹丸飞行姿态的测量.此外,靶场弹道测速雷达是一种单频连续波雷达,不具备RCS测量功能,通过RCS直接测量弹丸飞行姿态也是不可能的.
要利用雷达来测量弹丸飞行姿态,就必须使弹丸的飞行姿态角α(t)和β(t)与雷达回波信号r(t)之间建立明确的对应关系,这是解决问题的关键.通过理论分析和试验研究表明,对于普通弹丸不能够建立两者之间的对应关系.
弹道测速雷达发射水平线极化的电磁波.国内外有关专家提出利用雷达的线性极化特性在弹丸底部刻槽以测量旋转弹丸转速的方法[6,7].在采用弹丸底部刻槽法测量旋转弹丸转速的试验中,发现底部刻槽的旋转弹丸的雷达回波信号中有某种与弹丸运动特性相关联的周期性变化.通过试验分析和理论研究认为,在弹丸底部平面刻很窄、很深的槽,当旋转弹丸刻槽方向与电磁波极化方向平行时,雷达回波最强,垂直时雷达回波最弱.弹丸旋转在雷达回波上产生幅度调制,当电磁波与弹底平面入射角不同时,弹丸旋转在雷达回波信号中产生的幅度调制度不同.雷达回波信号幅度调制度与电磁波和弹轴夹角有关.因此,提出一种通过测量底部刻槽弹丸雷达回波信号幅度调制度来间接确定弹丸飞行姿态的设想.通过在弹丸底部刻槽,利用某种手段确定出电磁波与弹轴不同夹角时,相对应的幅度调制度关系.然后,将弹丸发射出去,雷达跟踪测量获得回波信号,通过对雷达回波信号的处理确定弹丸飞行过程中的幅度调制度.根据电磁波与弹轴的夹角和幅度调制度之间的关系,反求出弹丸飞行姿态角.这个方法就是利用雷达的线性极化特性,通过弹丸底部刻槽和高速旋转,在雷达回波信号中形成与弹丸飞行姿态相关的调制.通过对雷达回波信号的处理实现弹丸飞行姿态的测量.
2 弹丸的极化散射特性分析
为了实现从雷达回波中获得弹丸飞行姿态,需要在弹丸底部刻槽,使弹丸的散射场在雷达电磁波的激励下呈明显极化特性[8].下面在雷达发射水平线极化电磁波的情况下,弹丸高速旋转时,利用极化散射矩阵讨论极化特性弹丸的飞行姿态特征.
定义测量雷达和弹丸目标之间的几何关系如图1所示.在弹道初始上升段,雷达发射的电磁波主要照射弹丸的底部.图1中O′uvw为弹丸发射坐标系.坐标系Oxyz与O′uvw沿射向相差一个弹道倾角.假定测量雷达位于该坐标系的原点,发射的电磁波为沿着y轴正向传播的线极化均匀平面波,极化方向为Ox轴正向.弹丸底部中心位于坐标原点O,x轴与发射坐标系的v轴平行,y轴为对应时刻电磁波入射(雷达电轴)的方向,按照右手规则定义z轴.本文中弹丸的姿态采用相对雷达电轴的俯仰角α和方位角β表示,如图2和图3所示.
弹丸底部刻上若干具有一定深度的窄槽,弹丸的散射场将呈线极化特性.在初始时刻t0,刻槽方向如图2中粗实线AB所示,弹丸散射场极化方向AB在Oxy平面内.选择水平极化分量H为坐标轴Ox正方向,垂直极化分量V为坐标轴Oz正方向,则入射电场在H、V极化基下可以表示为

图1 测试雷达与目标弹丸之间的几何关系

图2 初始时刻弹轴与雷达电轴的几何关系
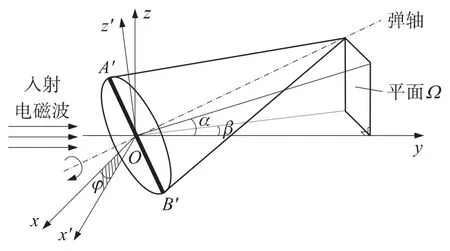
图3 旋转后弹轴与雷达电轴的几何关系
一般来说,旋转稳定弹丸绕其对称轴高速旋转,可认为在较短时间内,弹轴的空间指向不变,即飞行姿态不变.经过时间Δt,弹丸在Oxz平面内旋转角度的投影为φ,其散射场的极化方向变成A′B′,如图3所示.入射电场在x′、z′极化基下可以表示为

忽略交叉极化分量且经过远场近似,在x′、z′极化基下弹丸的极化散射矩阵可以表示为

式中,s‖(α,β)和s⊥(α,β)分别为Ox′yz′坐标系下散射场的极化方向平行和垂直于Ox′时弹丸的散射特性.
在x′、z′极化基下弹体散射场为
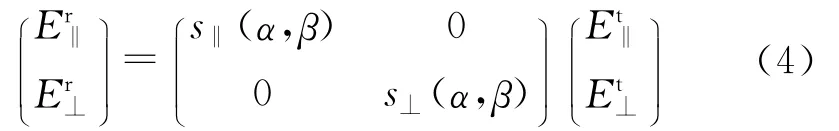
再将弹体的散射场变换回雷达发射电磁波的极化基下,即

根据天线的互易性定理,雷达接收到的回波在H、V极化基下表示为

式中,


由于雷达天线为水平线极化工作方式,仅接收水平极化的电磁波分量,因此有:

从式(7)可知,弹丸的姿态特征表现在s‖(α,β)和s⊥(α,β)中.二者仅与俯仰角α和方位角β有关,反映弹丸的飞行姿态信息.
利用倍角公式将式(7)展开整理,有:
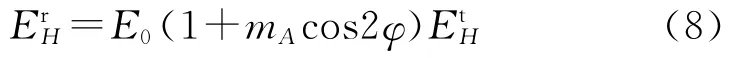
式中,

普通旋转弹丸为轴对称结构,其s‖(α,β)与s⊥(α,β)相等,弹丸旋转对散射场的影响很小.经刻槽处理后的弹丸s‖(α,β)与s⊥(α,β)具有很大的差异,使雷达回波信号呈现极化特性.
根据电场强度与电压的关系可知,其雷达回波可表示为如下幅度调制信号:

式中,A为雷达回波的幅度系数.
上述分析表明,雷达回波的调幅指数可做为弹丸姿态的直接观测量.调幅指数mA与弹丸飞行姿态有关,与雷达回波的强弱A无关,不受飞行距离的影响.在雷达回波的信噪比满足处理需求的前提下,从雷达回波信号中提取调幅指数,不要求雷达具有RCS和距离测量功能,这使得利用测速雷达测量弹丸飞行姿态成为可能.
3 弹丸飞行姿态测量原理
根据前述讨论,雷达回波调幅指数可表征弹丸飞行姿态,它可以通过处理雷达回波信号r(t)得到,即T:r(t)→mA(t).
如果能够事先确定出弹丸飞行姿态与调幅指数间的关系,则有可能获得弹丸飞行姿态角,但是,通常情况下无法确定弹丸飞行姿态与调幅指数间的映射关系.由于调幅指数是在新的特征空间中反映弹丸姿态与弹丸结构电磁特性的重要参数,已知弹丸姿态和弹丸结构就可以确定出调幅指数.通过某种技术手段可以建立弹丸飞行姿态到调制指数之间的映射关系F:α,β→mA.
下面讨论如何构建弹丸飞行姿态角与调幅指数之间的映射关系.当弹丸与雷达间的距离R不变时,雷达回波信号幅度变化与弹丸RCS成正比.这表明弹丸的RCS可用于构建弹丸飞行姿态角与调幅指数之间的映射关系.弹丸在不同姿态角α、β和旋转角φ下的RCS可以通过微波暗室测量或电磁场数值计算得到.保持姿态角α、β不变,依次得到随转动角φ变化的RCS序列,并从中处理出该姿态角下的调幅指数,进而可得到对应若干不同姿态角α、β的调幅指数mA.通过数据的曲面拟合,可构建弹丸姿态与回波调幅指数间的函数关系,在射击试验前实现调幅指数的标定.

式中,i<N,ui(α,β)为线性无关的多项式基函数,,D为设定的多项式阶数,ai为基函数的系数,F的形状如图5所示.
将由雷达回波中处理到的调幅指数m*A代入式(12),可以构造一个关于姿态角α和β的二元方程:

由于调幅指数mA是关于α和β的函数,通过一个观测值难以直接解算出两个姿态角,辅以弹丸螺旋进动的运动特性约束条件和多点数据拟合处理,可以解算出弹丸慢圆运动的姿态角.
首先,从弹丸回波调幅指数序列中处理出对应慢圆角运动的成分,以替换式(13)中的,构建一个关于慢圆运动姿态角的方程.而后,将弹丸进动近似为匀速圆周运动.调幅指数曲面关于方位轴和俯仰轴对称,如图5所示.调幅指数沿俯仰向变化较快,沿方位向变化较慢.弹轴进动一周,调幅指数曲线分别与方位轴和俯仰轴各相交2次.由于调幅指数曲面的等值曲线近似为椭圆形,弹轴与俯仰轴相交处的调幅指数对应曲线的极小值,与方位轴相交处对应曲线的极大值.查找出弹丸回波慢圆运动调幅指数序列的极大值和极小值即得到弹轴过俯仰轴和方位轴的时刻.相邻极值点的时间间隔Δt为在该象限内运动的总时间,对应弹丸慢圆角运动1/4周期.因此有:

式中,弹轴所处的象限号k=1,2,3,4;t为弹丸进入当前象限起经历的时间.
将式(13)与式(14)联立构成方程组,可以解算出弹丸飞行的慢圆姿态角.
4 仿真验证
图4为底部刻槽122 mm普通榴弹几何模型.刻槽方式为单条通槽,槽深7mm,槽宽2mm.根据弹丸模型,采用有限积分数值算法,以1°步进求出不同姿态角下的雷达散射截面积,再处理出弹丸回波调幅指数,并用最小二乘法拟合出调幅指数曲面,如图5所示.

图4 122mm底部刻槽弹丸模型

图5 最小二乘拟合生成的调幅指数曲面
为研究方便起见,参照文献[9],仅考虑起始攻角的贡献并引入章动衰减因子ρΔ,将弹丸的姿态表示为

式中,Δ0为起始章动角;ω1为快圆运动的角频率,ω2为慢圆运动的角频率;σe=1-(1/Sg),Sg为弹丸的稳定系数.
按照下述条件仿真弹丸飞行姿态.信号采样间隔取12.9μs,快圆周期取50ms,慢圆周期取1s.Δ0取2°,弹丸以匀速飞行,陀螺稳定因子Sg=2.6,章动衰减因子ρΔ=0.2,得到弹丸的飞行姿态曲线,如图6所示.按照姿态角曲线的弹丸运动规律和测速雷达的工作过程,处理得到如图7所示的调幅指数曲线.
根据前述分析,图7中的慢圆调幅指数曲线在极大值时刻t1、t3、t5对应β轴上的点,极小值时刻t0、t2、t4对应α轴上的点.
将α或β等于0分别代入式(13),可得到弹轴过坐标轴时的姿态角(0,β*)以及(α*,0).假定相邻极大值与极小值之间,α、β分别在[0,α*]和[β*,0]线性变化,以此作为弹丸飞行姿态角的初始值.假定在起始时刻弹丸处于α轴正向,弹丸右旋稳定.采用最优化方法求解由式(13)和式(14)构成的联立方程组,计算结果如图8所示.图中,Ⅰ、Ⅱ、Ⅲ、Ⅳ为象限号,与式(14)中k的取值相对应.由图8可知,采用本文方法解算出的弹丸飞行姿态与仿真的理论值能够较好地吻合.

图6 仿真的弹丸飞行姿态理论值

图7 仿真的调幅指数曲线
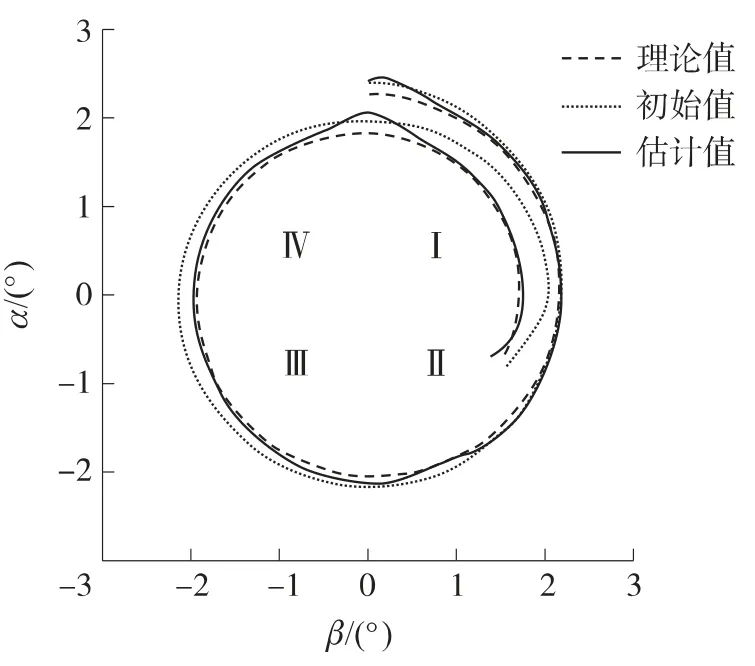
图8 弹丸飞行姿态的解算结果
5 结束语
在分析了旋转弹丸电磁散射特性的基础上,提出了一种基于极化特征的旋转弹丸飞行姿态测量方法.该方法通过在弹丸底部刻槽,使弹丸在雷达电磁波的激励下呈极化散射特性.利用弹丸回波的调幅指数mA(t)作为弹丸飞行姿态的直接观测量,通过仿真分析验证了方法的有效性.该方法扩展了弹底部刻槽获取目标运动信息的范围,对雷达目标特性研究有一定的借鉴作用.但是,该方法的应用有一定的局限性,仅适用于弹丸处于弹道上升直线段电磁波照射弹底的情况,存在由调幅指数曲面的轴对称性引入的象限模糊问题.目前该方法只能确定弹丸慢圆运动的姿态角,弹丸快圆运动的姿态角求解问题仍有待进一步研究.
[1]闫章更.射表技术[M].北京:国防工业出版社,2000.YAN Zhang-geng.Firing table technology[M].Beijing:National Defense Industry Press,2000.(in Chinese)
[2]HUGHSON M C,BLADES E L.Transonic aerodynamic analysis of lattice grid tail fin missiles,AIAA 2006-3651[R].2006.
[3]BROWN T G.Harsh military environments and micro electromechanical(MEMS)device[J].IEEE,2003,2:753-760.
[4]孙文峰.雷达目标识别技术评述[J].雷达与对抗,2001,(3):1-8.SUN Wen-feng,Review on radar target recognition[J].Radar& ECM,2001,(3):1-8.(in Chinese)
[5]CRAVEY R L.RCS measurements and simulation of a tethered satellite,NASA95-19781[R].1995.
[6]靳悦.弹头转速的全数字测量技术及仿真[J].指挥技术学院学报,1993,4(2):4-7.JIN Yue.Projectile spin’s completely digital measurement technical and limitation[J].Journal of Institute of Command and Technology,1993,4(2):4-7.(in Chinese)
[7]万建伟,周良柱,皇甫堪,等.测速雷达中的谱分析技术[J].弹道学报,1995,7(4),71-76.WAN Jian-wei,ZHOU Liang-zhu,HUANG Fu-kan,et al.The spectrum-analysing technology in measuring-speed radar[J].Journal of Ballistics,1995,7(4):71-76.(in Chinese)
[8]洪家财.底部刻槽旋转弹丸的RCS特性的分析与仿真[J].微波学报,2006,22(2):45-48.HONG Jia-cai.RCS analysis and simulation for bullet pill with slot[J].Journal of Microwave,2006,22(2):45-48.(in Chinese)
[9]宋丕极.枪炮与火箭外弹道学[M].北京:兵器工业出版社,1993.SONG Pi-ji.External ballistics of bullet,projectile and rocket[M].Beijing:Ordnance Industry Press,1993.(in Chinese)

