车载多管火箭炮发射系统基座的轻量化

林国问，马大为，朱孙科

（南京理工大学 机械工程学院，南京210094）

基座是车载多管火箭炮发射时的依托平台，它起着连接火箭炮转塔上部分与运载体的作用.在火箭炮发射时，会将发射时产生的燃气流冲击力、火箭炮自身的重力等载荷传递给运载体，其性能好坏直接影响着全炮的安全可靠性和射击时的精准性.随着现代战争对武器系统机动性提出的要求，轻量化成为武器系统的发展方向之一.

研究武器系统轻量化的方法很多，其中包括采用轻质高强材料、合理的简化结构及通过优化方法找寻结构合理的传力路径进行结构优化等.结构拓扑优化可以找寻结构合理的传力路径，它主要以提高结构性能或使结构轻量化为目标，在国际上，已经广泛地应用于飞机、汽车及其他机械产品的开发中，取得了很好的效果[1].目前结构拓扑优化的主要对象是连续变量的结构优化，比较成熟的方法[2，3]包括均匀化方法、变密度法和渐进结构优化方法等.

文中利用变密度法对基座的结构进行轻量化研究.对车载多管火箭炮发射时常用的典型射击工况，即最大射角下的基座进行拓扑优化，获得了约束条件下基座材料的最佳分布形式，结合工程要求建立了优化后的基座模型，并进行了刚强度校核和动力学响应分析，通过应用比刚度结构效能对优化前后的基座刚度进行了对比分析和炮口响应的研究，结果显示，用拓扑优化可以减轻基座的质量，同时对动态响应影响不大.优化方法可以应用于该产品的设计中，同时，对同类的产品结构设计具有参考意义.

1 拓扑优化的基本理论

拓扑优化设计技术能够在给定的设计空间内找出最佳的材料分布，拓扑优化能够大大改善结构的性能和减小结构的质量.连续体结构拓扑优化常用的方法是均匀化法和变密度法.变密度法[4～6]以连续变量的密度函数形式表述单元相对密度与材料弹性模量之间的对应关系，这种方法基于各向同性材料，不需引入微结构和附加的均匀化过程，程序实现简单，计算效率高，因此，本文采用变密度法对基座结构进行拓扑优化研究.

基于变密度法的拓扑优化理论[7]，其数学模型如下：

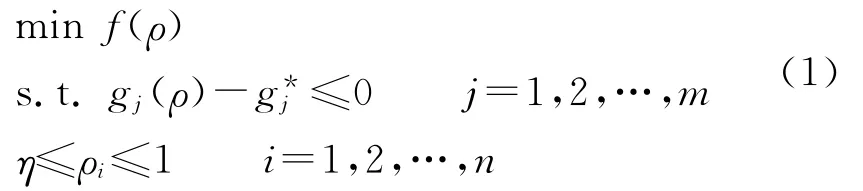
式中，f（ρ）为目标函数；ρi为单元的密度；gj（ρ）为第j个约束为约束上限；m为约束数；η是使刚度矩阵非奇异的极小正数，通常取为0.001[2]；n为总的单元数.

拓扑优化是一种0～1变量的复合优化问题，但在优化过程中有时会出现一种包含中间密度的情形，通常在优化控制中主要通过引入惩罚因子对其加以避免.惩罚因子在拓扑优化过程中能够有效地对中间密度值进行控制，使优化结构尽可能地呈现0和1的结构形式，从而使优化后的结构避免中间材料的出现.因此，为了获得0/1的密度分布，本文优化时采用幂指数公式[2，8]：

式中，Ki（ρ）和Ki分别为单元的惩罚刚度矩阵和真实刚度矩阵；p为惩罚因子，通常取2～4[9].

在结构拓扑优化问题中，棋盘格现象和网格依赖性是2个常见的数值不稳定问题.文中优化时采用文献[2，10]提出的最小成员尺寸控制（MMS），这有效地克服了拓扑优化过程中的棋盘格现象和网格依赖性.MMS理论可以抽象成：

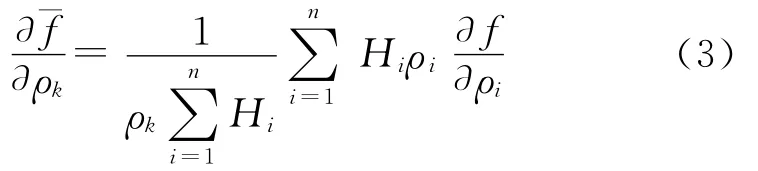
式中，网格独立加权因子Hi可表示为

式中，rmin为预设最小成员的半径；单元i和单元k为相邻的单元，d（i，k）为单元i和单元k之间的距离.

2 基座的拓扑优化

2.1 优化几何模型

基座结构的几何模型如图1所示，结构有承载面1，圆柱连接面2，加强筋3及与运载体固定面4.基座各部分之间主要通过焊接而成，通常焊缝及其热影响区的强度及刚性会比母材高，所以建模时将焊缝在几何上连接在一起处理，这与实际情况差别不大[2].由于基座结构在2个方向的尺寸明显大于第三个方向的尺寸，因此，在进行有限元分析时采用壳单元建立有限元模型，如图2所示.在图2中的特征点1位置，需要满足相关的设计和制造约束，在此忽略其变形，采用刚性单元来模拟，在特征点1位置施加载荷.

基座是通过钢板焊接而成，其设计要求为承载面在第一组4发弹齐射时，在巨大载荷作用下，承载面垂直方向的位移不大于1mm.

根据动力学计算，当发射角在最大射角时，第一组4发弹齐射时，承载面在垂直方向的位移为0.67mm.发射关键部位的位移小于设计要求，因此，有进行结构优化的余量存在.在基座进行拓扑优化时，应使关键部位的位移在设计的指定值范围内，而整体质量尽量小，从而达到轻量化的目的.

图1 基座的几何模型

图2 基座的有限元模型

2.2 优化模型设置

文中对基座优化模型设置为：

①以基座结构的质量最小化为目标函数；

②以承载面垂直方向允许的最大位移，即在第一组4发弹发射时，基座上表面在垂直方向的位移不大于1mm作为约束条件；

③以基座的相对单元密度为设计变量.

2.3 拓扑优化结果

本文借助Hyperworks中的Optistruct优化模块[11]优化基座结构，经过12次的迭代达到收敛，如图3所示，ms为结构质量，N为优化迭代次数.

图3 质量与迭代次数关系曲线

从图3可以看出，基座在前7次的迭代过程中质量大幅度地减小，到第8次迭代后计算基本收敛，质量不再减小，这说明基座初始结构中存在大量不起主要承载的材料.

结合基座的优化结果并考虑制造的可行性以及结构的对称性和美观性，同时以尽可能地减轻质量为目的，在基座圆柱面上开一个长方形孔以及上下各一个半圆孔，为了避免应力集中造成结构的损坏，结构的孔边界要求尽量圆滑，同时将优化中删除的加强筋予以加上，从而既使结构达到了美观和对称，又使结构的刚强度有所富裕和质量尽可能减小.拓扑优化结果如图4所示，优化后的几何模型如图5所示.

图4 基座优化结果

图5 基座优化后的几何模型

3 结果分析

3.1 刚强度分析

将优化后的基座结构进行刚强度校核，优化前后的分析参数分别如表1所示，其中σ和s分别为基座的最大应力和最大位移；β为比刚度结构效能.

表1 优化前后的参数

从表1中可知，尽管优化后的位移值比优化前有所增大，但都在设计的范围内.优化前后应力基本保持不变，均远小于材料的屈服极限.对于多管火箭炮来说，基座的结构相比于强度，高刚度在结构设计时显得更重要.因此，本文利用文献[12]中提出的比刚度结构效能β，对基座进行了比刚度分析.

式中，E为材料的弹性模量.

效能值越大，说明结构具有越高的单位质量刚度[2].从表1中可以看出，优化后的基座质量减小，而且优化后的比刚度结构效能大于优化前，说明优化后基座结构的单位质量的刚度裕度得到了改善.

3.2 动力学响应分析

将优化后的基座重新建模，并用于整炮动态响应分析，动力学仿真分析时，采用的是4－2发射方式，即先齐发第一组4发弹，待4发弹出管口且飞一段距离后在齐发第二组2发弹.弹性模量为210GPa，泊松比为0.3，密度为7 850kg/m3.图6为优化前后的整炮网格模型；图7为炮口响应曲线，图中，v1，v2分别为炮口偏航速度和俯仰速度；ω1和ω2分别为炮口偏航角速度和俯仰角速度.

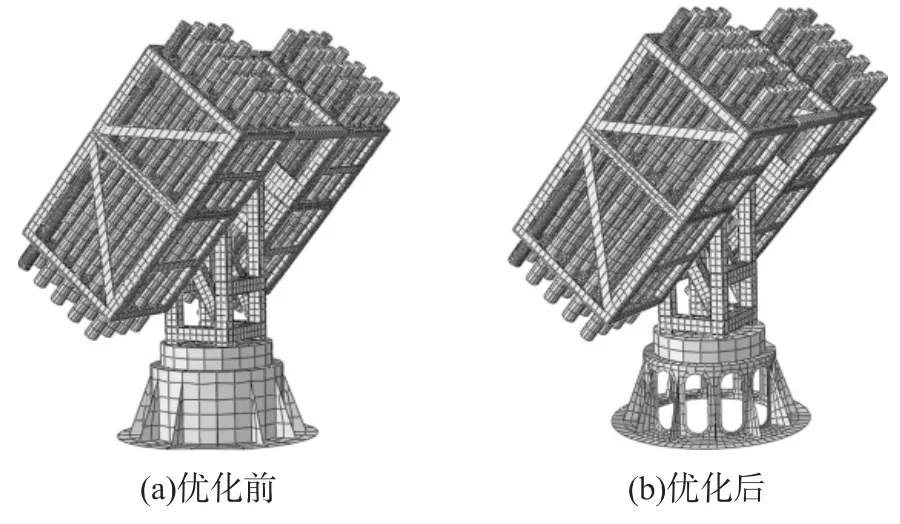
图6 优化前后整炮网格模型

图7 炮口响应分析

图7中曲线出现2次波动，主要是由2组弹先后发射所致，虚线表示基座采用原始结构，即原始模型；实线表示基座采用优化后的结构，即优化模型.从图7中可以看出，在整炮的动态响应分析中，优化前的基座和优化后的基座所产生的炮口响应变化不大，基本在一个数量级.因此，优化后的基座在满足刚强度后，在整炮的动力学响应分析中也能满足要求，对多管火箭炮的性能影响基本可以忽略.这说明对基座拓扑优化是可行的.

4 结论

文中针对车载多管火箭炮发射系统基座的轻量化问题，进行了基于变密度法的结构拓扑优化.对基座结构进行刚强度校核及动力学响应研究，结果显示，刚强度满足设计要求，优化前后的炮口响应无明显变化.优化设计后基座的质量得到了有效的减轻，减重达23%.相比于初始结构，优化后基座的效能值有所增加，表明基座的优化方案是有效的.该方法也可用于多管火箭炮其他部件的拓扑优化设计和轻量化研究.

[1]张胜兰，郑冬黎，郝琪，等.基于 Hyperworks的结构优化设计技术[M].北京：机械工业出版社，2007.ZHANG Sheng－lan，ZHENG Dong－li，HAO Qi，et al.Structural optimization design based on hyperworks[M].Beijing：China Machine Press，2007.（in Chinese）

[2]朱孙科，马大为，何勇，等.基于动力学仿真的舰炮基座结构拓扑优化设计[J].系统仿真学报，2007，21（20）：6 650－6 657.ZHU Sun－ke，MA Da－wei，HE Yong，et al.Topology optimization of naval gun seat based on dynamic simulation[J].Journal of System Simulation，2009，21（20）：6 650－6 657.（in Chinese）

[3]刘加光，陈义保，罗震，等.连续体结构的模糊多目标拓扑优化设计方法研究[J].系统仿真学报，2007，19（5）：1 095－1 099.LIU Jia－guang，CHEN Yi－bao，LUO Zhen，et al.Fuzzy multiobjective topology optimization of continuum strutures[J].Journal of System Simulation，2007，19（5）：1 095－1 099.（in Chinese）

[4]汤颖颖.基于变密度法的连续体拓扑优化设计[D].西安：长安大学，2008.TANG Ying－ying.Research on topology optimization methods of continuum structure based on variable density method[D].Xi’an：Chang’an University，2008.（in Chinese）

[5]刘晓梅.某特种车辆舱体结构的有限元分析与优化[D].南京：南京理工大学，2007.LIU Xiao－mei.Finite element analysis and optimization of one special vehicle cabin[D].Nanjing：Nanjing University of Science and Technology，2007.（in Chinese）

[6]崔明涛.不确定性连续体结构拓扑优化和柔性机构设计研究[D].西安：西安电子科技大学，2006.CUI Ming－tao.Research on topology optimization of continuum structures and design of compliant mechanisms with uncertainty[D].Xi’an：Xidian University，2006.（in Chinese）

[7]BENDSOE M P，SIGMUND O.Topology optimization theory，methods and application[M].New York，USA：Springer Press，2003.

[8]ZHOU M，PAGALDIPTI N，THOMAS H L，et al.An integrated approach to topology，sizing and shape optimization[J].Structural Multidisciplinary Optimization，2004，26（5）：308－317.

[9]ZHOU M，FLEURY R，SHYY Y K，et al.Progress in topology optimization with manufacturing constraints[C].Proceedings of the 9th AIAA/ISSMO Symposium on Multidisciplinary A－nalysis and Optimization.USA：AIAA，2002：1－8.

[10]ZHOU M，SHYY Y K，THOMAS H L.Checkerboard and minimum member size control in topology optimization[J].Structural Multidisciplinary Optimization，2001，21 （2）：152－158.

[11]于开平，周传月，谭惠丰.HyperMesh从入门到精通[M].北京：科学出版社，2005.YU Kai－ping，ZHOU Chuan－yue，TAN Hui－feng.HyperMesh：from intrudction to master[M].Beijing：Science Press，2005.（in Chinese）

[12]岑海棠.结构仿生理论、轻质零件结构仿生设计及RP工艺验证[D].北京：北京航空航天大学，2004.CEN Hai－tang.Study on structural bionics theory，lightweight structure bionics design and rapid prototyping testing[D].Beijing：Beijing University of Aeronautics Engineering and Astronautics，2004.（in Chinese）