改性单基发射药内弹道模型
张江波,王琼林,张玉成
(西安近代化学研究所,西安710065)
随着科技工业的发展、新武器的涌现,身管武器向着高初速、高威力、远射程的目标发展,这使得作为武器能源物质的发射药朝着高能量、高强度、高装填密度、高燃烧渐增性的方向发展.改性单基发射药(EI发射药)是在单基药的基础上,通过后续新的工艺处理,既增加发射药能量,又提高燃烧渐增性,实现单基发射药的第二次生命力.改性单基发射药以硝化棉为主要组分,工业基础雄厚,且具有低烧蚀、低温度系数的特点,能够大幅度提高火炮炮口的动能水平,瑞士已经研制成功并推广应用[1~3],王琼林在这方面的研究也已经取得了较大的进展[4,5].改性单基发射药基础理论研究尤其是燃烧内弹道模型理论研究正逐步深入.
本文对改性单基发射药基础理论中的内弹道理论进行了深入研究.通过分析改性单基发射药的结构特征,建立了双气源项内弹道模型,制备了浸渍含量为15%的样品,并进行了内弹道试验验证,对改性单基发射药的不同影响因素进行了计算分析,结果表明,所建立的双气源项内弹道模型能够很好地反映改性单基发射药的内弹道过程.
1 改性单基发射药结构特征分析
改性单基发射药采用压伸浸渍的制备工艺进行制备.首先压出单孔、七孔等不同药型形状的以硝化棉为基本能量组分的均质单基发射药,然后通过浸渍高能组分(主要是硝化甘油)材料使得能量得到大幅度提升,为降低初始燃速,在表面浸渍一薄层钝感剂,最后在表面包覆一层均匀的高性能改性材料,完成整个制备过程.改性单基发射药的结构如图1所示.

图1 改性单基发射药结构图
根据改性单基发射药的制备工艺过程及图1的结构图(5/7改性单基发射药横切和剖切的显微图片)知,改性单基发射药具有如下的结构特征:①药粒整体为非均质发射药;②药粒表层(发射药外圆周面及两端面)浸渍深度较深,小孔内部浸渍深度较浅;③浸渍浓度和深度服从一定的规律;④药粒较均质单基发射药粒(基体药粒)外形尺寸上有一定程度的增大;⑤发射药内层未浸渍部分为均质硝化棉层;⑥外层由浸渍层组成,内层由浸渍层和均质层组成,内层和外层共同组成改性单基发射药.
2 内弹道模型的建立
2.1 内弹道燃烧过程
由改性单基发射药的结构特征知,改性单基发射药燃烧过程明显分为2层:内层开始为一薄层浸渍层燃烧,后为均质层燃烧,整个内层主要由均质层组成;外层全部由浸渍层组成,在燃烧过程中始终为浸渍层.将符合以上结构特征的发射药燃烧称为双层燃烧,其具体内涵为:装药床瞬时全面同时着火,发射药外层和内层同时燃烧,外层在特定火药力和燃速条件下按平行层燃烧定律燃烧,内层在特定火药力和燃速条件下,按平行层燃烧定律燃烧,但是,由于火药力分布和燃速分布跟药粒内部特定位置有关,所以,在时间相同的条件下,内外层燃烧的厚度不同.这样双层燃烧模型可以描述具有不同内外层结构特征的发射药燃烧过程.
假设内弹道过程按经典内弹道过程处理,燃烧服从双层燃烧模型,则发射药起始燃烧开始,炮膛内将有不同燃速的双气源相,即内层气源相和外层气源相.双气源相的能量推动弹丸做功,此燃烧过程称为双气源相双层燃烧过程.当发射药燃烧完毕后,按经典内弹道中第二阶段处理,即发射药燃气膨胀做功.
2.2 内弹道数学模型
为定性地描述整个物理过程,需要进行以下假设[6~7]:
①改性单基发射药服从双气源相双层燃烧模型,内层和外层均服从平行层燃烧;
②内外层火药力分布、浸渍浓度与深度之间服从某一特定函数关系式;
③药体中火药力分布与浸渍浓度分布具有相同类型的函数形式;
④改性单基发射药燃烧特性与浸渍深度之间服从某一特定函数关系式;
⑤其它假设同经典内弹道理论模型中的假设[6].
改性单基发射药服从双气源项燃烧模型,内层浸渍深度为xn,孔径内表层为坐标0,向弧厚内延伸为正,外层浸渍深度为xw,药粒外表层为坐标0,向弧厚内延伸为正,即采用对向双坐标描述浸渍量、火药力、燃烧特性与深度的关系,则外层火药力为fw(xw)=Fw(xw),其中Fw(xw)=fI+fJcJ(xw),fI为均质层火药力,fJ为浸渍层火药力,cJ(xw)为浸渍量在浸渍层中的质量百分数分布,xw∈[0,xw,b],xw,b为外层燃烧结束边界.内层火药力为fn(xn)=Fn(xn),其中Fn(xn)=fI+fJcJ,n(xn),cJ,n(xn)为浸渍量在浸渍层中的质量百分数分布,xn∈[0,xn,b];fn(xn)=fI,其中xn∈[xn,b,(2e1-xw,b)],则内层燃速为un=u1,n(xn)pn1,n(xn),u1为 燃 速 系 数,n1为燃速指数,u1,n为内层燃速系数,2e1为火药弧厚.
外层燃速为uw=u1,w(xw)pn1,w(xw).
在某一时间t时,燃烧的相对厚度为Zn(t)=此时xn=unt,xw=uwt.则改性单基发射药的内弹道方程如下.火药燃速方程:
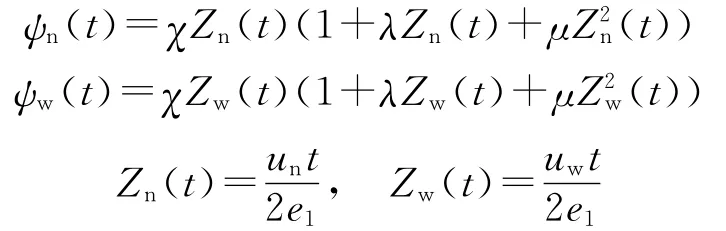
弹丸运动方程:

能量平衡方程:

式中,ψn为内层燃烧百分数;ψw为外层燃烧百分数;χ,λ,μ为火药形状函数;S为火炮横断面积;p为炮膛压力;ω为装药量;ρ为发射药密度;α为发射药余容;Δ为装填密度;l0为药室缩颈长;m为弹丸质量;v为弹丸速度;l为弹丸行程长;φ为次要功系数,γ为火药比热比.
初边值条件:xw∈[0,xw,b],xn∈[0,xn,b],在任意时刻t有,xw=uwt,xn=unt,l∈[0,lg],对以上内弹道方程组进行求解即可获得改性单基发射药内弹道数值解.采用C++编制了计算程序并进行了弹道计算.
3 结果及讨论
3.1 理论计算及试验验证
以某30mm口径火炮为研究对象开展了理论计算并进行了试验验证,表1和表2分别为某30mm口径火炮构造诸元及改性单基发射药特征参量、理论计算及内弹道实验结果.表中V0为药室容积,lg为身管 长 度,φ为 硝 化 甘 油 浸 渍 量;tp,max为 最大压力时间,pmax为最大压力,v0为炮口初速,t为弹丸运动时间.

表1 30mm火炮构造诸元及改性单基发射药特征参量

表2 理论计算及内弹道实验结果
由表1知,制备的改性单基发射药浸渍量为15%时,实测平均火药力为1 080kJ/kg(采用密闭爆发器试验求得的表观总体平均火药力).由表2知,在装药量为103g时,30mm火炮试验最大膛压为333.69 MPa,炮口初速为888.5 m/s,弹丸在膛内运动时间为4.17 ms,运动到最大膛压处的时间为1.23ms.计算和试验结果对比分析知,关键特征参量最大误差项为膛压,误差为0.76%.从图2中知,理论计算p-t曲线和试验p-t曲线基本重合,理论计算与试验结果对比表明,本计算模型能够很好地反映改性单基发射药的燃烧特性及内弹道过程.
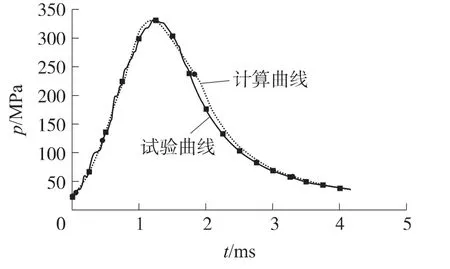
图2 理论计算与试验p-t曲线
3.2 浸渍量为不同分布函数的计算
为了能够对内弹道进行定量计算,需给出部分条件(下同),假定NG浸渍量为20%,由于浸渍程度的不均匀性,基体药的火药力为980kJ/kg,假定外层浸渍层火药力最高为1 300kJ/kg,火药力和浸渍浓度具有相同类型的分布函数且服从以下函数形式:y1=-440x2+140x+1 300,y2=-1 400x2+1 400x+1 000,y3=-440x2+740x+1 000.定义y1为左抛物线型,y2为正抛物线型,y3为右抛物线型.在外层浸渍深度相对值Zw1为0~1范围中的火药力函数曲线如图3所示.

图3 不同分布函数曲线
浸渍量为不同分布函数时的内弹道计算结果如表3所示.

表3 浸渍量为不同分布函数的弹道计算结果
由表3知,采用y1、y2、y3分布函数时,最大膛压分别为350MPa,354MPa,347MPa,初速分别为844m/s,848m/s,854m/s.与y1分布函数结果对比分析知,y2分布函数结果在最大膛压增加4 MPa时,初速提高了4m/s;y3分布函数结果在最大膛压降低3 MPa的情况下,初速提高了10m/s.由图4知,p-t曲线随分布函数y1,y2,y3的变化呈现整体向右倾斜的变化.从表3知,出现最大膛压的时间分别为0.91ms,0.94ms,0.98ms,且依次增大,这表明改性单基发射药的燃烧渐增性随着分布函数的变化在不断增加.图5也很好地证实了这一点,y3的v-t曲线呈现明显的前低后高趋势,即在550m/s之前较y1,y2曲线低,在550m/s之后位于y1,y2曲线之上.计算结果表明,在其它参数一定的条件下,浸渍量的分布函数对改性单基发射药的弹道性能有着较大的影响,分布函数呈现前低后高的情况下,最大膛压在较低的条件下,能够实现更高的初速.要想获得较好的内弹道效果,浸渍量浓度分布函数需服从右抛物线类型的函数.

图4 浸渍量为不同分布函数的p-t曲线
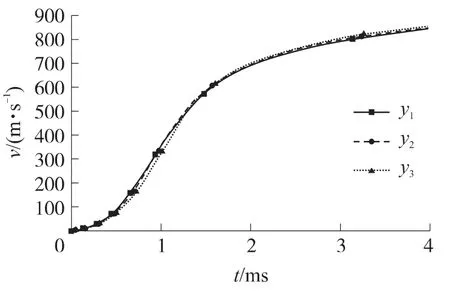
图5 浸渍量为不同分布函数的v-t曲线
3.3 不同浸渍量的计算
假设浸渍量分别为5%,15%,25%,浸渍量分布函数采用y3抛物线型,外层浸渍层火药力最高分别约为1 100kJ/kg,1 200kJ/kg,1 350kJ/kg,弹道计算结果及曲线如表4及图6、图7所示.
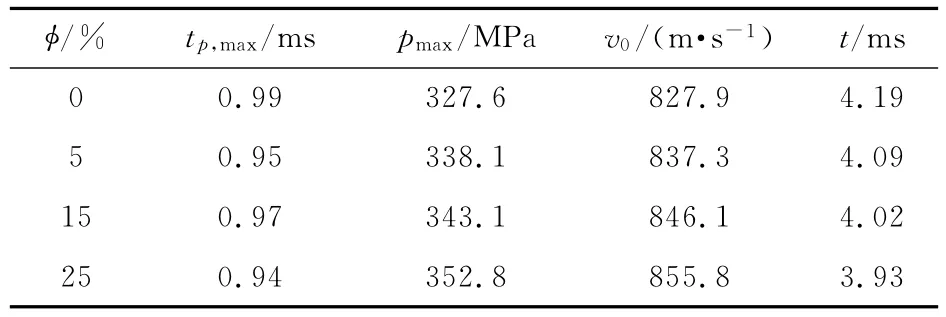
表4 不同浸渍量的弹道计算结果
由表4知,浸渍量为0%,5%,15%,25%时,最大膛压分别为327.6MPa,338.1MPa,343.1MPa,352.8 MPa,初速分别为827.9 m/s,837.3 m/s,846.1m/s,855.8 m/s.与0%浸渍量对比知,最大膛压分别增加了10.5 MPa,15.5 MPa,25.2 MPa,初速分别增加了9.4 m/s,18.2 m/s,27.9 m/s,这表明随着浸渍量的增加最大膛压和初速按一定比例同时增加.由图6、图7知,浸渍量为25%的p-t曲线在最大膛压前向左倾斜,表明起始燃烧速度较快,燃烧渐增性较差,使得最大膛压增高且提前出现(浸渍量为25%时tp,max为0.94 ms,浸渍量为0%时tp,max为0.99ms),内弹道整体做功环境变差,浸渍量为25%的v-t曲线一直位于最上也表明了这一点.计算结果表明,改性单基发射药随着浸渍量的增加,最大膛压和初速在不断增加,燃烧渐增性降低,内弹道整体做功环境变差.因此,在增加浸渍量提高发射药能量的同时,必须采用钝感包覆等相关工艺进行燃烧渐增性改善,单纯地增加浸渍量并不能得到理想的内弹道效果.

图6 不同浸渍量的p-t曲线
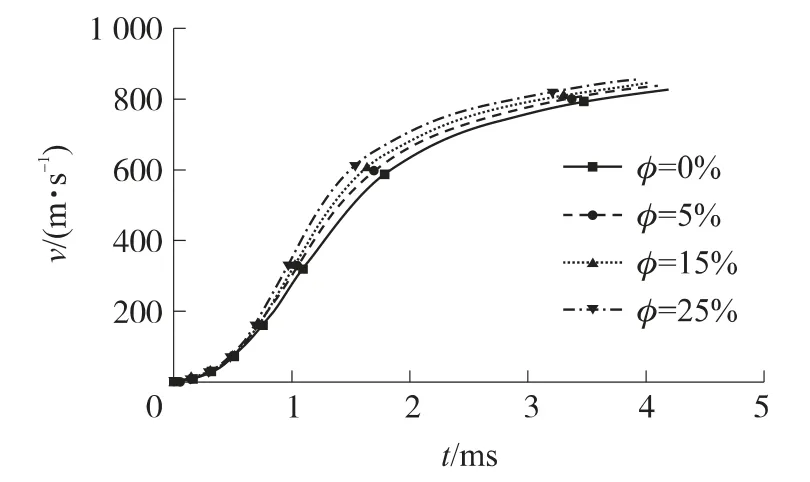
图7 不同浸渍量的v-t曲线
3.4 不同浸渍深度的计算
假设浸渍深度与外层厚度的比K=0.3,0.6,0.9,浸渍含量为25%,浸渍分布函数服从y3抛物线型,弹道计算结果及曲线如表5和图8、图9所示.
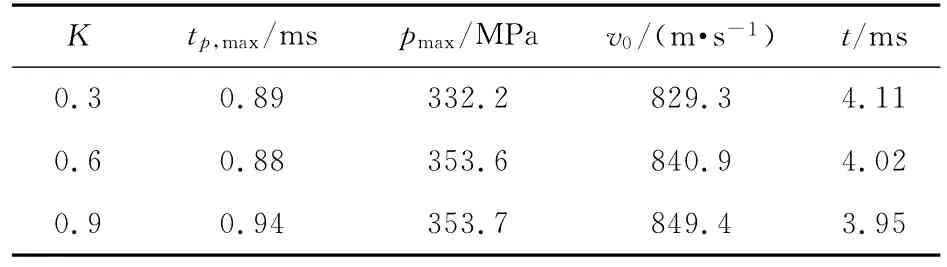
表5 不同浸渍深度比的弹道计算结果

图8 不同浸渍深度比的p-t曲线
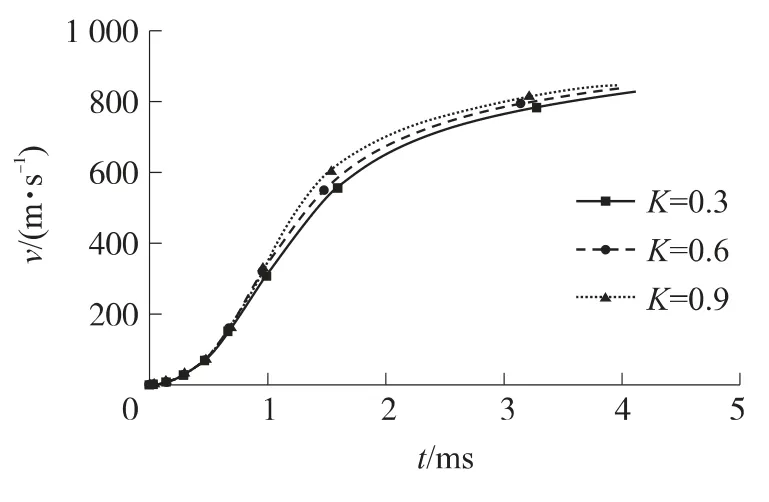
图9 不同浸渍深度比的v-t曲线
由表5知,K为0.3,0.6,0.9时,最大膛压分别为332.2MPa,353.6MPa,353.7MPa,初速分别为829.3m/s,840.9 m/s,849.4 m/s.K为0.6时最大膛压比0.3时增加了22.4 MPa,初速提高了11.6m/s,K为0.9时最大膛压比0.6时增加了0.1 MPa,初速提高了8.5m/s,这表明随着浸渍深度的增加初速在不断增加,最大膛压在浸渍深度增加到某一值时将不再变化,浸渍深度存在某一临界阈值,当浸渍深度达到该值时,初速增加而最大膛压不增加,该算例中,K为0.6和0.9时的最大膛压基本相等.由图8、图9知,K为0.9时,p-t曲线最大值右侧一段范围内明显高出其它2条曲线,说明K为0.9的燃烧渐增性较好,K为0.9的v-t曲线高于其它2条曲线也证明了这一点.因此,在改性单基发射药制备过程中应增大浸渍深度,当达到浸渍深度临界阈值后,能够得到初速和燃烧渐增性增加而最大膛压不增加的内弹道效果.
4 结论
本文制备了改性单基发射药,基于试验建立了双气源燃烧内弹道模型并进行了数值计算,主要得到以下结论:
①建立了改性单基发射药的双气源项内弹道模型,30mm火炮试验结果表明,所建立的模型很好地反映了改性单基发射药的内弹道特点;
②浸渍量浓度的分布函数对改性单基发射药的弹道性能有着较大的影响,在服从呈现前低后高的右抛物线类型条件下,能够实现较低的最大膛压和更高的初速;
③浸渍深度存在临界阈值,当达到浸渍深度临界阈值(文中计算参数下K为0.6)后,能够得到初速和燃烧渐增性增加而最大膛压不增加的内弹道效果.
[1]梁勇,王琼林,于慧芳,等.增能钝感单基药的燃烧特性[J].含能材料,2007,15(6):597-599.LIANG Yong,WANG Qiong-lin,YU Hui-fang,et al.Combus-tion properties of the energy-increased desensitized single-base propellant[J].Chinese Journal of Energetic Materials,2007,15(6):597-599.(in Chinese)
[2]熊立斌,应三九,罗付生.高效液相色谱法测定单基球扁药中钝感剂的含量[J].火炸药学报,2001,24(2):54-55.XIONG Li-bin,YING San-jiu,LUO Fu-sheng.Determination of the deterrents in the single-base oblate spherical powder by high-performance liquid chromatography[J].Chinese Journal of Explosives & Propellants,2001,24(2):54-55.(in Chinese)
[3]代淑兰,许厚谦,肖忠良.带制退器的膛口燃烧流场并行数值模拟[J].弹道学报,2009,21(4):84-87.DAI Shu-lan,XU Hou-qian,XIAO Zhong-liang.Numerical simulation of muzzle combustion flow field with brake by parallel computation[J].Journal of Ballistics,2009,21(4):84-87.(in Chinese)
[4]马方生,廖昕,王泽山.催化剂对太根发射装药燃烧性能的影响[J].弹道学报,2011,23(1):9-12.MA Fang-sheng,LIAO Xin,WANG Ze-shan.Effect of catalyst on combustion property of TEGDN propellant charge[J].Journal of Ballistics,2011,23(1):9-12.(in Chinese)
[5]王琼林,刘少武,潘清,等.小尺寸枪药表面高分子钝感剂浓度分布测试研究[J].火炸药学报,2000,23(3):13-15.WANG Qiong-lin,LIU Shao-wu,PAN Qing,et al.Study on determination of polymer deterrent concentration profile in small-sized gun propellant[J].Chinese Journal of Explosives &Propellants,2000,23(3):13-15.(in Chinese)
[6]张江波,张玉成,蒋树君,等.多层发射药内弹道模型及数值求解[J].火炸药学报,2009,32(3):83-85.ZHANG Jiang-bo,ZHANG Yu-cheng,JIANG Shu-jun,et al.The interior ballistic model and numerical simulation of multilayer charge[J].Chinese Journal of Explosives & Propellants,2009,32(3):83-85.(in Chinese)
[7]马忠良,李志良,萧忠良,等.药型尺寸对变燃速发射药燃烧渐增性的影响[J].含能材料,2007,15(2):128-130.MA Zhong-liang,Li Zhi-liang,XIAO Zhong-liang,et al.Effect of grain size on progressive combustion of the variable burning rate propellant[J].Chinese Journal of Energetic Materials,2007,15(2):128-130.(in Chinese)

