一类多重和的计算公式

冷慧廷，郑德印

（杭州师范大学理学院，浙江杭州 310036）

一类多重和的计算公式

冷慧廷，郑德印

（杭州师范大学理学院，浙江杭州 310036）

结合组合解释和Vandermonde卷积公式，研究关于两类二项式系数的多重和式计算问题，所得结果包含Butler（2010）的新近结论作为特例.

多重和；嵌套和；组合证明

0 引 言

关于多重和的计算问题，国内外的学者已经做了很多研究，S.Butler［1］在2010年发表了一篇关于嵌套和的文章，得到了关于多重和的几个计算公式，如

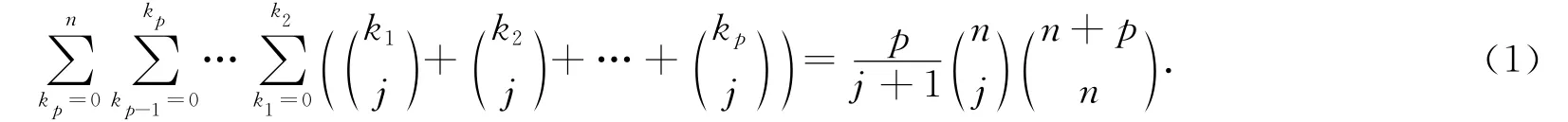
本文将利用组合解释和Vandermonde卷积公式研究如下2种形式的多重和：

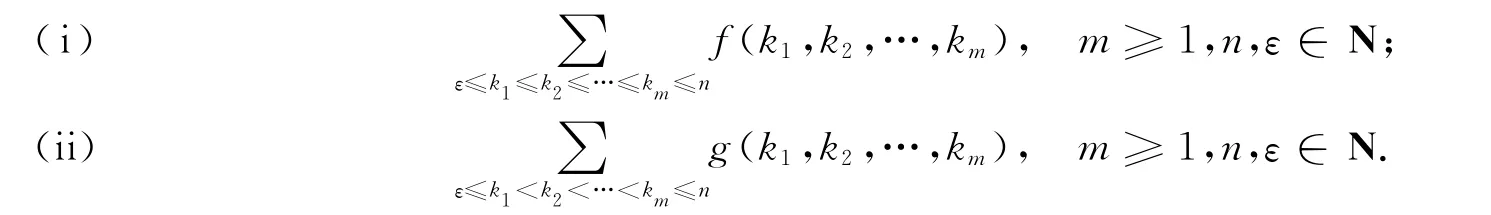
其中，f，g为包含m个变量的多元函数.容易看出和（i）的求和指标可重复而和（ii）的求和指标不可重复，得到封闭和公式是困难且复杂的，但对某些特殊的f，g其封闭和还是比较简单漂亮的.本文先使用组合解释给出二项式系数的一种多重和表示，在此基础上研究了求和指标可重复和不可重复的两类多重和式的计算问题，其中求和项是二项式系数或二项式系数的和，并考虑了f，g为某些二项式系数的情形，其结果以Butler的结果为特例.下面先给出几个引理.

有限集合N的一个m－组合或m－块B就是N的m个元素的非空子集，用Bm（N）表示N的m－子集的集合.

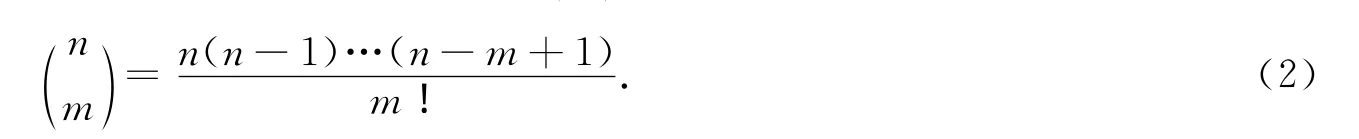
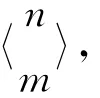
假设集合N＝｛1，2，…，n｝，ki∈N，则

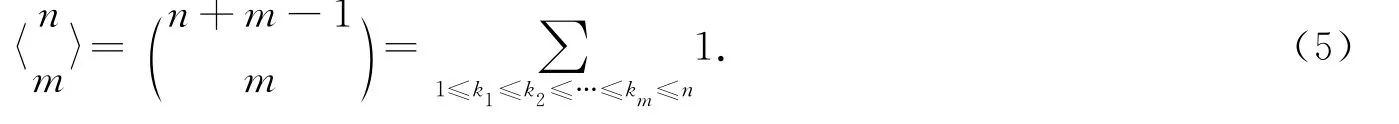
1 求和指标可重复的多重和

上述式（13）和（14）为特例.笔者重新推证了由Butler［1］所发现的定理2中的两个恒等式，式（13）就是引言中的式（1）.

2 求和指标不可重复的多重和

以下考虑（ii）型的多重和计算问题.

3 小 结

本文仅考虑了m重和（i）和（ii）的求和项f和g为二项式系数或二项式系数的和的情形.实际上，也可考虑其他形式的f和g的求和问题，限于篇幅，这里不再一一赘述.

［1］Butler S，Karasik P.A note on nested sums［J/OL］.Journal of Integer Sequences，2010，13（4）［2011－04－30］.http：//www.emis.ams.org/journals/JIS/VOL13/Butler/butler T.pdf.

［2］王天明.近代组合学［M］.大连：大连理工大学出版社，2008：7－12.

Computing Formulas of a Class of Multi－Sum

LENG Hui－ting，ZHENG De－yin

（College of Science，Hangzhou Normal University，Hangzhou 310036，China）

With combinatorial explanation and Vandermonde convolution formula，this paper investigated the computing formulas of multi－sum concerning two classes of binomial coefficient.The results obtained contain the Butler's new conclusions as special cases.

multi－sum；nested sum；combinatorial proof

O157.1 MSC2010：05A15

A

1674－232X（2012）01－0051－05

10.3969/j.issn.1674－232X.2012.01.011

2011－05－23

郑德印（1964—），男，副教授，主要从事组合数学、超几何级数和特殊函数研究.E－mail：deyinzheng＠yahoo.com.cn