一般伪黎曼流形的2－调和类空超曲面

范胜雪，宋卫东

（安徽师范大学数学计算机科学学院，安徽芜湖 241000）

一般伪黎曼流形的2－调和类空超曲面

范胜雪，宋卫东

（安徽师范大学数学计算机科学学院，安徽芜湖 241000）

研究了一般伪黎曼流形中的2－调和类空超曲面，获得此类超曲面的J.Simons型积分不等式及一些Pinching结果.

伪黎曼流形；2－调和映照；类空超曲面

0 引 言

按J.Eells和Lemaine在文献［1］中设想，姜国英在文献［2］中讨论了Riemann流形间的2－调和映照，欧阳崇珍又在文献［3］中将2－调和映照推广为从黎曼流形到伪黎曼流形的情形，并在该文的第四部分探讨了常曲率Lorentz流形的2－调和类空超曲面.本文将其外围流形推广到一般伪黎曼流形的情形，获得以下一些结果.

定理1 设Nn＋1为指标是1的（n＋1）维完备连通的伪黎曼流形，其截面曲率KN满足0＜δ≤KN≤1.Mn为Nn＋1紧致定向的2－调和类空超曲面，则成立如下积分不等式：

定理2 在定理1条件下，若还满足下列条件之一：

i）若0≤S＜nδ；

ii）若S＞n且H＝const.

则Mn为极大类空超曲面.

1 预备知识

本文约定各类指标的取值范围如下：

若无特殊说明，重复指标表示关于该指标在取值范围内求和.

设Nn＋11为截面曲率KN满足条件0＜δ≤KN≤1的（n＋1）维完备连通伪黎曼流形，Mn为等距浸入到的类空超曲面，选取上的局部伪黎曼幺正标架场｛eA｝，使得限制在Mn上时，｛ei｝与Mn相切，令｛ωA｝为其对偶标架，｝为的联络1－形式，于是在Mn上时，有

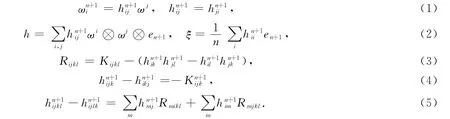
其中h，ξ，Rijkl，KABCD分别为Mn的第二基本形式、中曲率向量、曲率张量及的曲率张量为的一阶和二阶共变导数，定义为

分别为Mn的第二基本形式模长平方及中曲率.

为定理证明需要，给出以下两个引理：

引理1［3］Mn为伪黎曼流形的2－调和类空超曲面的充要条件：

仿［4］的证明，对于伪黎曼流形，有

引理2［4］设为（n＋1）维伪黎曼流形，对x∈M，有δ≤KN≤1，则在x处有

2 定理证明

由前面的有关公式，可得

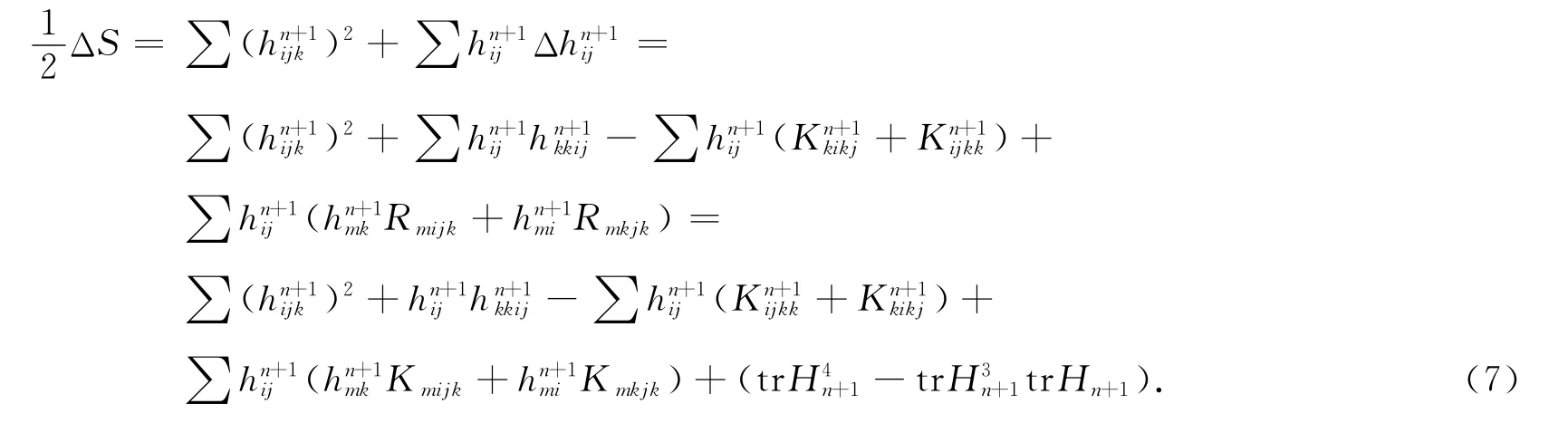
首先将式（6）第一式改写成

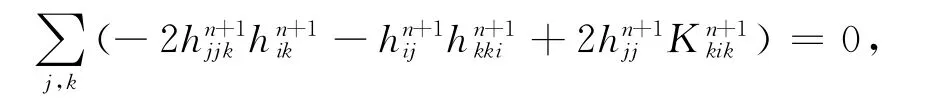
两端关于i求导，并对i求和得

调整指标，结合式（6）第二式可得

以上完成定理1的证明.

若

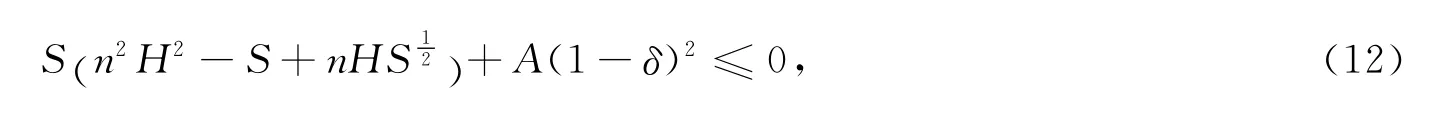
［1］Eells J，Lemaire L.Seleted topics map［M］//Providence R I.CBMS.50.Washington DC：AMS，1983.

［2］姜国英.Riemann流形间2－调和的等距浸入［J］.数学年刊，1986，7A（2）：130－144.

［3］欧阳崇珍.伪黎曼空间型的2－调和类空子流形［J］.数学年刊，2000，21A（6）：649－654.

［4］Golderg S I.Curvature and homology［M］.London：Academic Press，1962.

2－Harmonic Space－Like Hypetsurface in Pseudo－Riemannian Manifolds

FAN Sheng－xue，SONG Wei－dong
（College of Mathematics and Computer Science，Anhui Normal University，Wuhu 241000，China）

This paper studied the 2－harmonic space－like hypersurface in pseudo－Riemannian manifold，obtained integral inequality of J.Simons'type and some Pinching results.

pseudo－Riemannian manifold；2－harmonic map；space－like hypersurface

O186 MSC2010：53C20

A

1674－232X（2012）01－0056－04

10.3969/j.issn.1674－232X.2012.01.012

2011－07－04

安徽省教育厅自然科学基金项目（KJ2008A05ZC）.

宋卫东（1958—），男，教授，主要从事微分几何研究.E－mail：swd＠sina.com