G－度量空间中几个新的不动点定理

周书行，谷 峰

（杭州师范大学理学院，浙江杭州 310036）

G－度量空间中几个新的不动点定理

周书行，谷 峰

（杭州师范大学理学院，浙江杭州 310036）

在G－度量空间中，利用局部化单调定理，证明了几个新的不动点定理，所得结果进一步丰富和发展了G－度量空间中的不动点理论.

G－度量空间；局部化单调函数；局部化单调定理；不动点

1 引言和预备知识

1992年，Dhage［1］引入了D－度量空间的概念，企图得到和度量空间中相类似的一些结果.随后，Dhage［2－5］给出了D－度量空间的拓扑结构和几个不动点定理.然而，Mustafa和Sims［6］的结果表明，关于D－度量空间的大多数基本拓扑性质是不正确的，这使得Dhage在D－度量空间中得到的许多结果是无效的.因此，Mustafa［7］提出了G－度量空间的概念，此后，文献［8－10］进一步讨论了G－度量空间中的不动点问题.本文利用郭伟平［11］给出的局部化单调定理，证明了G－度量空间中的几个新的公共不动点定理，从而进一步发展了G－度量空间中的不动点理论.

定义1［8］设X是非空集合，G：X×X×X→［0，∞），满足：

（G1）如果x＝y＝z，则有G（x，y，z）＝0；

（G2）∀x，y∈X，x≠y，有G（x，x，y）＞0；

（G3）∀x，y，z∈X，y≠z，有G（x，x，y）≤G（x，y，z）；

（G4）G（x，y，z）＝G（x，z，y）＝G（y，z，x）＝…（关于3个变元对称）；

（G5）∀x，y，z，a∈X，G（x，y，z）≤G（x，a，a）＋G（a，y，z）.

称函数G是X上的一个广义度量，或称G是X上的一个G－度量，称（X，G）为G－度量空间.

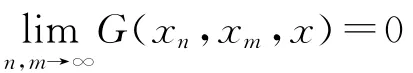
命题1［8］设（X，G）为G－度量空间，则以下结果等价：

（i）序列｛xn｝G－收敛于x；

（ii）G（xn，xn，x）→0（n→∞）；

（iii）G（xn，x，x）→0（n→∞）；

（iv）G（xn，xm，x）→0（n，m→∞）.

命题2［8］设（X，G）为G－度量空间，则（X，dG）为度量空间，其中

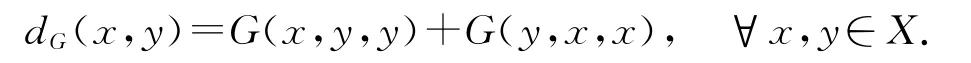
由G和dG的定义不难得到下面的不等式成立：

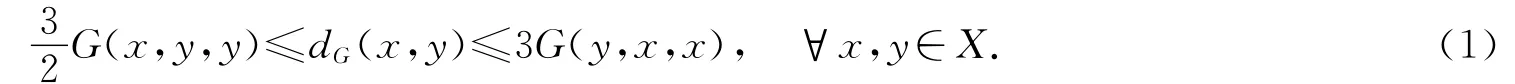
由命题1和式（1）易知，序列｛xn｝G－收敛于x当且仅当dG（xn，x）→0（n→∞）.可见G－度量空间一定是度量空间，并且它们有相同的收敛性.

命题3［8］设（X，G）是一个G－度量空间，则函数G（x，y，z）关于所有3个变元是连续的.

定义3［11］设X是一非空集合，T是X上的自映像，L：X→［0，∞），A⊂X，若对∀x∈A，当L（x）＞0时，L（Tx）＜L（x）；当L（x）＝0时，L（Tx）＝L（x）.则称L为A上的局部单调函数.当A＝X时，称L为X上的局部单调函数.

定义4 设X是一非空集合，称函数g：X×X×X→［0，∞）满足条件（g），如果（g）：g（x，y，z）是三元连续函数，且g（x，y，z）＝0的充分必要条件是x＝y＝z.

定义5 称函数f：［0，∞）→［0，∞）满足条件f，如果f：f（t）＜t，当t＞0时.

定义6［8］称G－度量空间（X，G）是对称的G－度量空间，如果G（x，y，y）＝G（y，x，x），∀x，y∈X.

引理1［11］（局部化单调定理） 设X是一度量空间，T为X到自身的连续映像，且存在x0∈X，使｛Tnx0｝n≥0有一个聚点p，若存在X上的局部单调的连续函数L且L－1（0）唯一，则p为T在X中的唯一不动点.

2 主要结果

定理1 设T为G－度量空间（X，G）到自身的连续映像，若存在x0∈X，使｛Tnx0｝n≥0有一个聚点p，且存在函数g满足条件（g），以及

（i）∀x，y，z∈X，x≠y≠z有

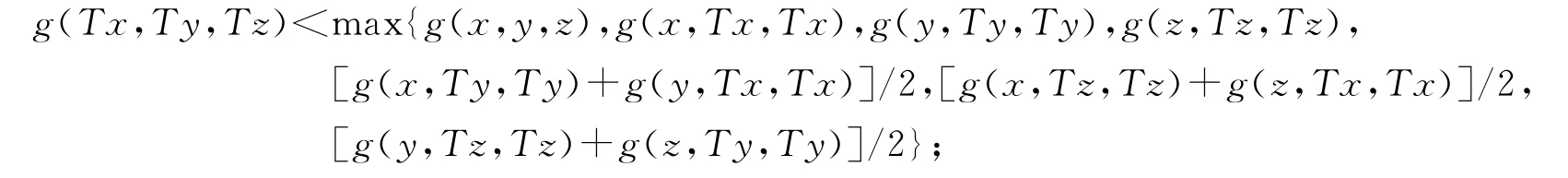
（ii）∀x∈X，有

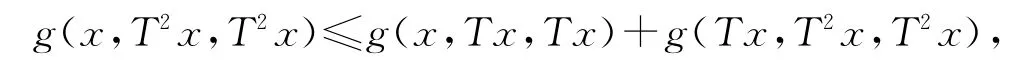
则p为T在X中的唯一不动点.

证明 设L（x）＝g（x，Tx，Tx），∀x∈X，由T，g的连续性可知L为X→［0，∞）的连续函数.

1）若L（x）＝0，由g满足（g）条件可知x＝Tx，从而L（Tx）＝L（x）.

2）若L（x）＞0，则x≠Tx，于是由条件（i）和（ii）可得

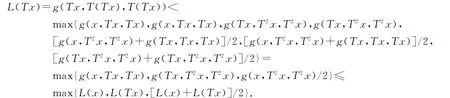
若L（Tx）≥L（x），则由上式可得L（Tx）＜L（Tx），此为矛盾.故有L（Tx）＜L（x）.这样就证明了L为X上的局部单调函数.

对x0∈X，由L为X上的局部单调函数可知

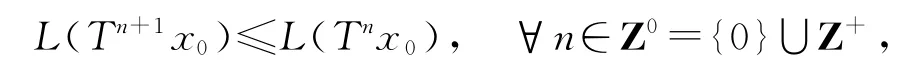
故｛L（Tnx0）｝n≥0单调递减有下界，从而数列｛L（Tnx0）｝n≥0收敛.由假设条件｛Tnx0｝n≥0有一个聚点p，不妨设Tnix0→p，p∈X.再由T，L的连续性，可得

注意到｛L（Tnx0）｝n≥0收敛，故L（p）＝L（Tp）.

我们断言L（p）＝0.若不然，有L（p）＞0，由L的局部单调性可得L（Tp）＜L（p），这与L（p）＝L（Tp）矛盾.故必有L（p）＝L（Tp）＝0，即L－1（0）存在.

现在证明L－1（0）是唯一的.事实上，设L（p）＝L（q）＝0且p≠q，则由函数g的性质和L（x）的定义可得p＝Tp，q＝Tq.于是由（i）可得

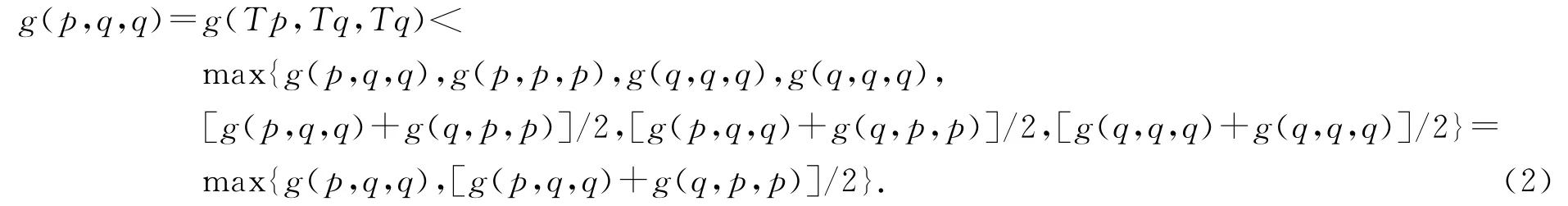
若g（p，q，q）＞g（q，p，p），则由式（2）可得g（p，q，q）＜g（p，q，q），此为矛盾.故必有g（p，q，q）＜g（q，p，p）.在式（2）中交换p，q的位置同理可得g（p，q，q）＞g（q，p，p），这是不可能的，故必有p＝q.从而L－1（0）唯一.于是由引理1即得定理1的结论.定理1证毕.

推论1 设T为G－度量空间（X，G）到自身的连续映像，若存在x0∈X，使｛Tnx0｝n≥0有一个聚点p，且∀x，y，z∈X，x≠y≠z有

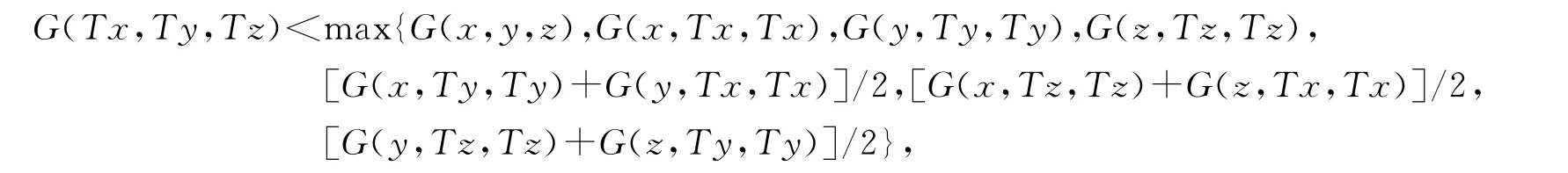
则p为T在X中的唯一不动点.

证明 在定理1中取g（x，y，z）＝G（x，y，z），则由函数G的性质可知定理1中的条件（ii）成立，故由定理1得推论1的结论成立.

定理2 设T为G－度量空间（X，G）到自身的连续映像，若

（i）存在x0∈X，使｛Tnx0｝n≥0有一个聚点p；

（ii）存在函数f和g分别满足条件（f）和条件（g），使得

则p是T的唯一不动点.

证明 设L（x）＝g（x，Tx，Tx），∀x∈X，由T，g的连续性可知L为X→［0，∞）的连续函数.下面证明L为X上的局部单调函数，且L－1（0）唯一.事实上，

1）若L（x）＝0，由g满足（g）条件可知x＝Tx，从而L（Tx）＝L（x）.

2）若L（x）＞0，则x≠Tx，于是由条件（i）和（ii）可得

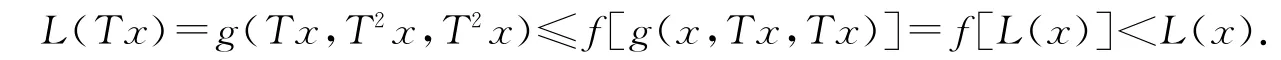
这说明L为X上的局部单调函数.仿定理1可证L（p）＝L（Tp）＝0，即L－1（0）存在.

现在证明L－1（0）是唯一的.若不然，设L（p）＝L（q）＝0，但p≠q，则g（p，q，q）＞0，再由条件（ii）有

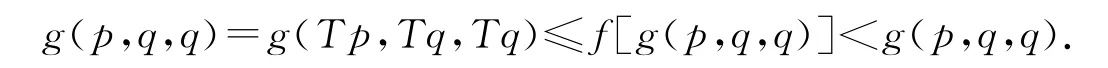
此为矛盾.故必有p＝q，从而L－1（0）唯一.于是由引理1即得定理2的结论.定理证毕.

定理3 设T为G－度量空间（X，G）到自身的连续映像，若存在x0∈X，使｛Tnx0｝n≥0有一个聚点p，且∀x，y，z∈X，x≠y≠z有

则p为T在X中的唯一不动点.

证明 与定理1证明类似，在此略去.

［1］Dhage B C.Generalized metric spaces and mappings with fixed point［J］.Bull Calcutta Math Soc，1992，84（4）：329－336.

［2］Dhage B C.Generalized metric space and topological structure I［J］.An Stiint Univ Al I Cuza Iasi Mat（N.S），2000，46：3－24.

［3］Dhage B C.On generalized metric spaces and topological structure II［J］.Pure Appl Math Sci，1994，40（1/2）：37－41.

［4］Dhage B C.On continuity of mappings in D－metric spaces［J］.Bull Cal Math Soc，1994，86：503－508.

［5］Dhage B C.Generalized D－metric spaces and multi－valued contraction mappings［J］.An Stiint Univ Al I Cuza Iasi Mat（N.S），1998，44：179－200.

［6］Mustafa Z，Sims B.Some remarks concerning D－metric spaces［C］//Proceedings of International Conference on Fixed Point Theory and Applications.Spain：Yokohama Publishers Valencia，2004：189－198.

［7］Mustafa Z.A new structure for generalized metric spaces with applications to fixed point theory［D］.Ph D thesis，The University of Newcastle，Callaghan，Australia，2005.

［8］Mustafa Z，Sims B.A new approach to generalized metric spaces［J］.J of Nonl Convex Anal，2006，7（2）：289－297.

［9］Mustafa Z，Obiedat H，Awawdeh F.Some fixed point theorem for mapping on complete Gmetric spaces［J］.Fixed Point Theory and Applications，2008，Article ID 189870.

［10］Mustafa Z，Sims B.Fixed point theorems for contractive mappings in completeG－metric spaces［J］.Fixed Point Theory and Applications，2009，Article ID 917175.

［11］郭伟平.局部化单调定理［J］.内蒙古师范大学学报：自然科学版，1990，19（3）：19－22.

Some New Fixed Point Theorems inG－metric Spaces

ZHOU Shu－hang，GU Feng

（College of Science，Hangzhou Normal University，Hangzhou 310036，China）

Using the localized monotone theorem，the paper obtained some new fixed point theorems inG－metric space.The results further enriched and developed the fixed point theorem inG－metric space.

G－metric spaces；localized monotone function；localized monotone theorem；fixed point

O177.91 MSC2010：47H10；54H25

A

1674－232X（2012）01－0047－04

11.3969/j.issn.1674－232X.2012.01.010

2011－07－09

国家自然科学基金项目（11071169）；浙江省自然科学基金项目（Y6110287）；杭州师范大学研究生教改基金项目.

谷 峰（1960—），男，教授，主要从事非线性泛函分析及应用研究.E－mail：gufeng99＠sohu.com