简化滚动轴承变速箱体的显示动力学分析

郑隆龙

（重庆大学机械传动国家重点实验室，重庆 400030）

滚动轴承是机械设备中承受载荷和传递运动十分重要的部件，但由于在力传递过程中滚动轴承的内外圈接触变形，滚动体的接触状态十分复杂，很难建立精确的有限元模型，实现滚动轴承应力状态的求解。

为准确地获得行驶过程中车辆变速箱中的受力状态，本文提出了一种滚动轴承的分析方法，考虑了轴承自身的几何参数、材料特性，还需考虑轴承载荷、转速、润滑油等因素。

建模时，将滚动轴承中滚子模拟为弹性元件，连接变速箱齿轮轴和刚性壳体，把计算的轴承刚度赋予弹性元件。齿轮轴啮合产生的振动，通过刚性壳体传递给变速箱，从而对箱体轴承接触部位进行显示动力学分析。

1 滚动轴承的刚度计算

1.1 滚动轴承的受力分析

在模拟简化轴承滚子为弹性元件过程中，需要考虑滚动轴承在载荷的作用下产生对应的变形，即计算轴承的刚度（如图1）。

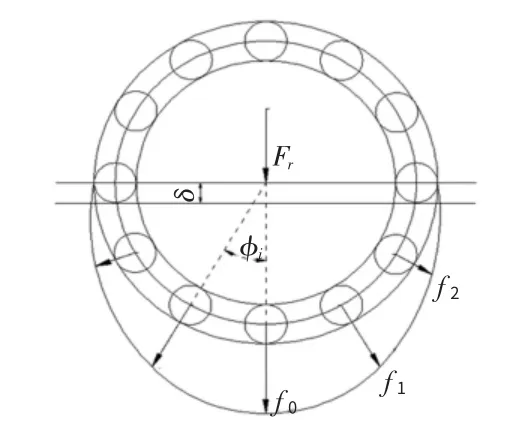
图1 轴承径向载荷作用下的载荷分布

图中，

Fr为径向载荷；

δ为轴承内外圈的相对位移；

准i为第i个滚子中心线与径向载荷方向之间的夹角；

fi为与径向载荷方向之间夹角为准i的滚子承受的接触载荷。

由受力平衡，可得

1.2 根据Hertz理论计算接触变形

轴承在载荷作用下的接触变形，是滚子和内圈之间的弹性变形δ1与滚子和外圈之间的弹性变形δ2之和，即

由图1所示，在径向载荷Fr的作用下，由hertz理论，轴承滚动体与内外圈接触区域为椭圆，接触区应力呈半椭球体分布，用半逆解法并通过积分变换，对线接触问题给出方程求解[1]。

设Z为滚子的数目，r为滚子半径，R1和R2分别为内外圈滚道半径，E为弹性模量，Fr为径向载荷，滚子和内外圈的有效接触长度为l。

则滚子与内圈和外圈的接触变形分别为

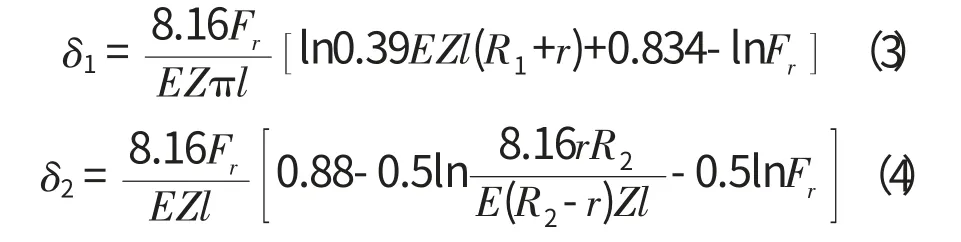
令

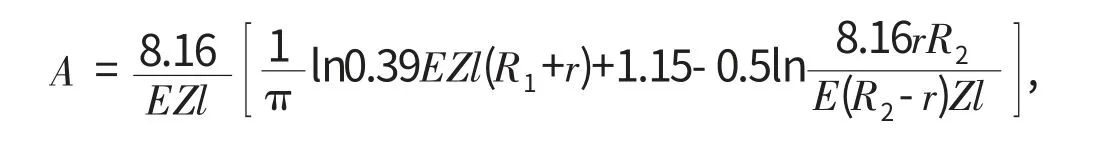
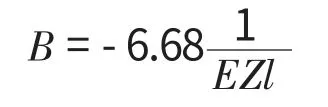
则Hertz接触总变形为

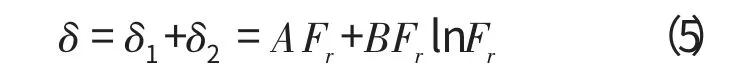
1.3 静态Hertz接触下的轴承刚度

圆柱滚子轴承的刚度，是指在外载荷作用下，轴承内外圈在载荷方向上产生的相对位移[3]。即轴承的刚度

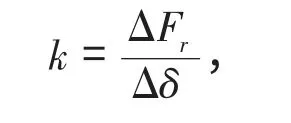
则处于静态的滚动轴承接触刚度计算公式

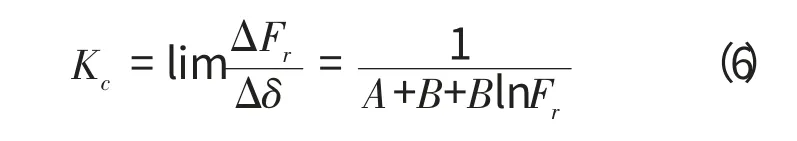
1.4 滚动轴承的油膜刚度

滚动轴承在实际运转过程中，由于润滑油的存在，滚子与内圈和外圈接触的部位分别会有一层油膜，导致了滚动轴承中心实际的位移发生改变，同时改变了滚动轴承的刚度。

设滚子与内圈和外圈之间的油膜厚度分别为h1和h2，利用Dowson-Higginson公式计算，最小油膜厚度分别为[3]

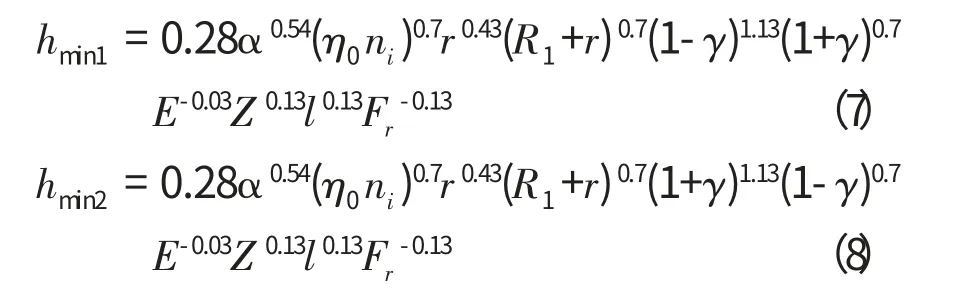
其中，

α为润滑油粘压系数，（1/Pa）；

η0为润滑油在大气压下的动力粘度（Pa·s）；

ni为内圈转速；

r为滚子半径；

R1为内圈半径；

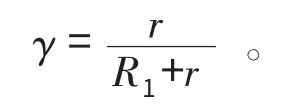
设

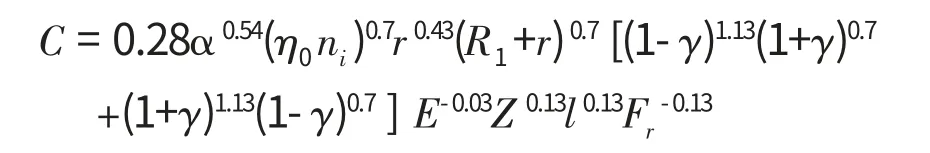
则

所以，滚动轴承的油膜刚度为

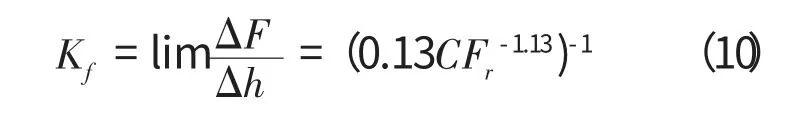
1.5 滚动轴承的刚度

综上可知，滚动轴承的刚度，实际上为外载作用下同时考虑滚子与内外圈的变形和油膜弹性体的变形共同作用的结果。滚动轴承的刚度是由Hertz理论的接触刚度和油膜刚度串联而成[4]，即

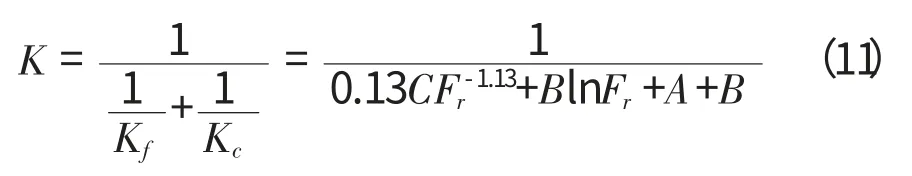
2 有限元分析计算

2.1 有限元模型的建立

以某公司MF524型变速箱为研究对象，建立其有限元模型。如图2、图3所示。

图2 齿轮箱整体模型

图3 箱体中齿轮轴模型

MF524有5个齿轮轴，每个齿轮轴通过2个轴承与变速箱箱体相连。

本文主要进行箱体轴承接触部位的动力学分析，不考虑齿轮轴啮合应力变化，将箱体有限元模型设为柔性体，齿轮轴模型设为刚性体。模型建成后共有34万个柔性单元。轴承简化模型，一般将滚子设为一个弹性元件[10]或Gap单元[5]，使滚子两端与内外圈固定相连，但此时轴承不能转动，只能进行静力学分析。

为了实现轴承接触应力的显示动力学有限元分析，本文将内圈固定在齿轮轴上，将滚子简化为弹性杆，弹性杆的一头与齿轮轴相连。将外圈简化为一层刚性壳网格，与弹性杆的另一端相连，如图4所示。

图4 模拟轴承示意图

并且这层壳网格与箱体轴承支撑处接触，产生相对运动。

2.2 模型的约束加载和边界条件

将变速箱固定在3档档位，约束变速箱上下半部接触部分网格的6个自由度，将其固定；约束齿轮轴5个自由度，使其只能绕轴心转动。将图中轴承外圈壳体网格与箱体的接触方式在Hypermesh中用contact_automatic_surface_to_surface。

MF524变速箱最大输入扭矩为250 N·m，最大输入转速为6 500 r/min。输入初始力矩为0，在0.2 s后扭矩匀速加载到150 N·m，无阻力矩。计算时长为0.2 s，步长为200。将齿轮轴挡位调到3档处，扭矩加载在变速箱与发动机链接轴，即第三轴，输入的初始转速为3 000 r/min。

根据输入轴的转速和各个啮合齿轮的传动比，计算出各个轴的转速。已知MF524是由GCr15轴承钢制造，

弹性模量E=2E11，

油的粘度η0=0.02 Pa·s，

粘压系数α=2.3×10-8Pa-1，

再由轴承滚子数量和尺寸Dw、l，可求得每个轴承的A、B、C的值，代入式（11），计算出轴承刚度，将此刚度赋予弹性杆。

由式（11）可以计算出变速箱中10个轴承的刚度，图（3）中齿轮轴从左至右分别为1～4轴，后方为5轴，如表1所示。

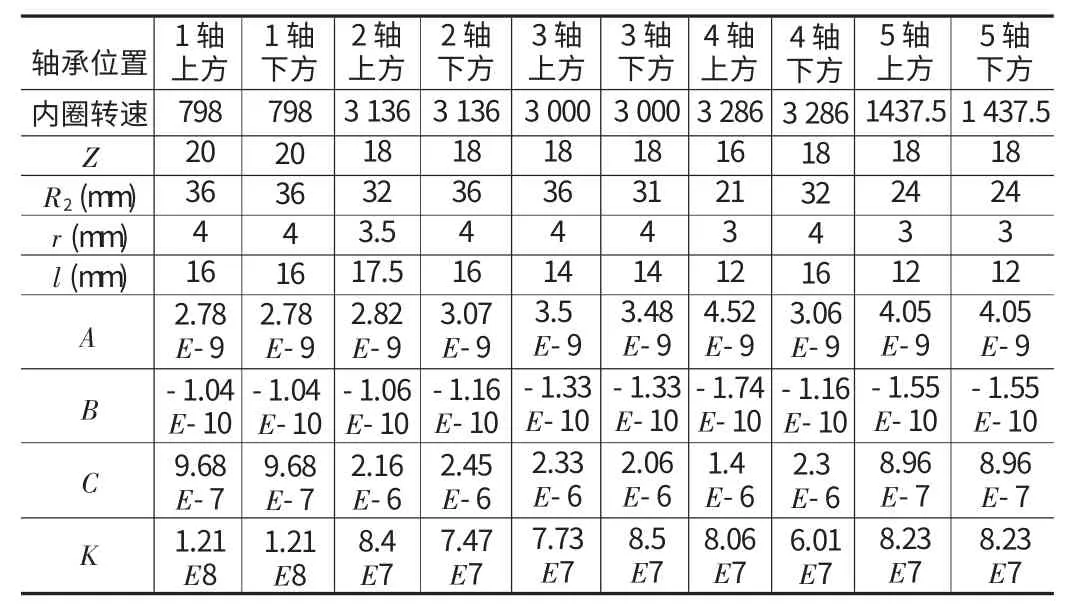
表1 轴承参数及计算刚度

3 分析结果及讨论

利用显式动力分析程序ls-dyna进行计算。变速箱箱体的最大应力，一般分布在主轴轴承与箱体的接触部分，或者几何形状突变的部位。分别在主轴的两个轴承与上下箱体的接触部分选取测点，导出应力图。

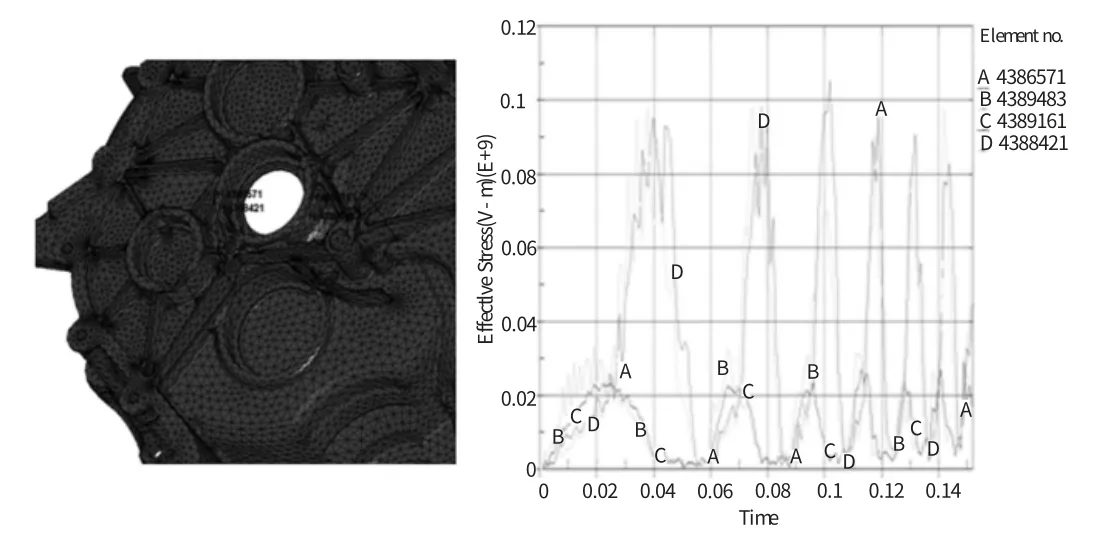
图5 变速箱体与主轴轴承4个测点分布与von mises stress

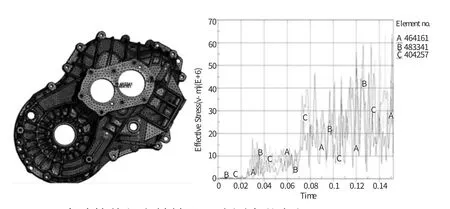
图6 变速箱体与主轴轴承3个测点分布与von mises stress

而实际仿真结果，如图7所示，变速箱体的高应力区域主要集中在主轴、即输入轴轴承接触部分的箱体附近。

图7 变速箱箱体von mises stress分布图

图8 轴承滚子接触应力图

观测变速箱齿轮转速的变化情况（如图9所示）。

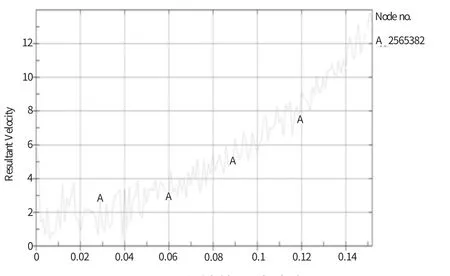
图9 主轴外圈线速度

由分析结果可知，变速箱体的应力随齿轮轴旋转成周期变化，齿轮轴旋转越快，箱体应力越大。箱体主轴轴承附近承载了较大的应力。而滚子轴承的应力，主要集中在滚体与内圈接触的位置，与文献相符[5]。

4 结束语

针对圆柱滚子轴承的特点，通过力学分析，考虑弹性流体对轴承刚度的影响，得出了滚动轴承的刚度的理论计算方法。轴承的刚度由接触刚度和油膜刚度串联而成，与轴承的材料、尺寸、转速、油膜性质等相关，表现出非线性变化。

变速箱体受力最大的区域，在主轴轴承附近，而轴承的主要应力分布区域，主要集中在内圈和轴承接触的部分。由仿真结果可知，轴承附近的箱体最大应力约为105 MPa。

[1]吴云鹏，张文平，孙立红.滚动轴承力学模型的研究及其发展趋势[J].轴承，2004，（7）：44-46.

[2]樊 莉，谭南林，沈栋平.基于显示动力学的滚动轴承接触应力有限元分析[J].北京交通大学学报，2006，（8）：109-112.

[3]吴 昊，安 琦.弹流润滑圆柱滚子轴承径向刚度的计算[J].轴承，2008，（1）：1-4.

[4]唐云冰，罗贵火，章璟旋，等.高速陶瓷滚动轴承等效刚度分析与实验[J].航空动力学报，2005，（4）：240-244.

[5]杜 静，黄 文，李成武.基于GAP单元的滚动轴承应力分析[J].机械设计与制造，2011，（6）：43-45.

[6]蒋立冬，应丽霞.高速重载滚动轴承接触应力和变形的有限元分析[J].机械设计与制造，2008，（10）：62-64.

[7]张乐乐，高 祥，谭南林.基于ANSYS/LS-DYNA的滚动轴承仿真与分析[J].机械设计，2007，（9）：62-65.

[8]林腾蛟，荣 崎，李润方.深沟球轴承运转过程动态特性有限元分析[J].振动与冲击，2009，（1）：118-122.

[9]刘 宁，张 钢，高 刚.基于ANSYS的圆柱滚子轴承有限元应力分析[J].轴承，2006，（12）：8-10.

[10]杨德华，顾伯忠，崔向群.一种双列调心球面轴承刚度的计算及应用[J].轴承，114-117.