扇及其一致膨胀图的PI指数*

何丽丽， 黄 敏， 郝建修

(浙江师范大学数理与信息工程学院，浙江金华 321004)

0 引言

Wiener(W)指数和Szeged(Sz)指数均用于反映有机分子的某些结构特征．PI指数是一个类似于Wiener指数的拓扑指数，PI指数在实际生产和生活中有着非常广泛的应用．例如，文献［1］介绍了PI指数用于描述有机分子的毒性(QSTR)和活性(QSAR);文献［2-3］讨论了通过计算一些纳米结构的PI指数以深入探究其特性等．

本文主要研究简单连通图的PI指数．一个图G的PI指数定义为

其中：对于边e=uv，neu(e|G)表示G中到点u的距离比到点v的距离更近的边的数目;nev(e|G)是指G中到点v的距离比到点u的距离更近的边的数目;求和符号表示取遍G中所有边．G中与点u和点v距离相等的边不计入e的PI指数．将neu(e|G)简记为neu．

1 预备知识

本文相关的一些基本定义详见文献［4-5］．

定义1［5］图 G 为扇当且仅当 V(G)={vi|i=0，1，2，…，n}，E(G)={v0vi|i=1，2，…，n}∪{vivi+1|i=1，2，…，n-1}，此时图 G 可记为 Fn．且易得，|E(Fn)|=2n-1．

定义2［5］对一个图G，设V(G)={v1，v2，…，vn}，G的膨胀图FG定义为：G的一个顶点vi对应到FG的一个顶点集 Vi，且 V(FG)={vij|vij∈Vi，i=1，2，…，n，j=1，2，…，ti，|Vi|=ti∈Z+}，vijvkl∈E(FG)，j=1，2，…，ti，l=1，2，…，ti当且仅当 i=k 或 vivk∈E(G)．显然，当 t1=t2= … =tn=1 时，FG=G．若t1=t2=…=tn=t，则称FG为G的一致膨胀图，记作UFG．

定义3［2］设图G是一个连通的简单图，对任意的边e=uv∈E(G)，定义ne为G中与点u和点v距离不相等的边的数目．

定义4［4］设A，B 为图G 中的点集，定义［A，B］为G 中点集A与点集B 间的边，|［A，B］|表示A与B间的边数．

定义5 设边e=uv∈E(G)，定义d(e)=d(uv)=d(u)+d(v)-2，其中d(u)和d(v)分别为点u和点v在图G中的度．

2 主要结果

定理1 对n≥3，有 PI(Fn)=2n2+2n-8．

证明 容易验证，PI(F3)=16，PI(F4)=32．因此，当n=3，n=4时，定理1成立．

下证当n≥5时定理1也成立．将 Fn的边分别记为 e2i-1=v0vi，e2i=vivi+1，i=1，2，…，n，如图1所示．

图1 Fn扇

由定义3可得

故当n为奇数时，

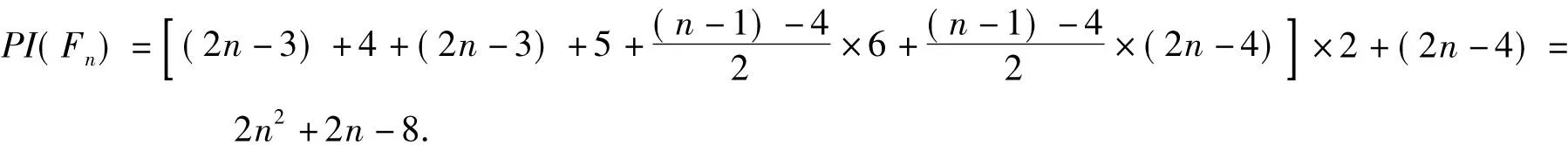
当n为偶数时，

定理1得证．

其中，t如定义2所定义．

证明 由于UFF1和UFF2为完全图，因此容易验证此时定理2成立．

下面将图UFFn的边分2种情形讨论．

1)e∈［Vi，Vi］(i=0，1，2，…，n)．设 e=uv，易见，UFFn中不与 e关联的边与点 u 和点 v等距．故此时ne等于 d(e)，亦即 ne=d(u)+d(v)-2．因此

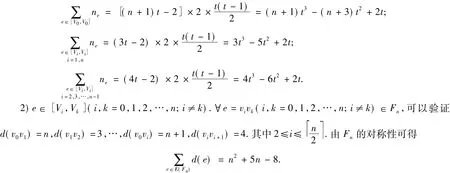
对于边 v0jv1l∈UFFn，［V0，Vi］中关联于 v0j的边和［V1，V2］中关联于 v1l的边均与点 v0j和点 v1l不等距，其中 i=1，2，…，n．然而，Fn中其他对 e=v0v1的 PI指数有贡献的边此时膨胀为［Vi，Vk］(i，k=3，4，…，n，i≠k)中的 t2条边，且［V0，V0］和［V0，V1］中各存在 t-1 条边关联于 v0j，［V1，V1］和［V1，V0］中也各存在t-1条边关联于v1l．V3，V4，…，Vn中的边均与点v0j和点v1l不等距．因此，由定义3可以验证

由PI指数的定义可得

因此，综合1)和2)可得

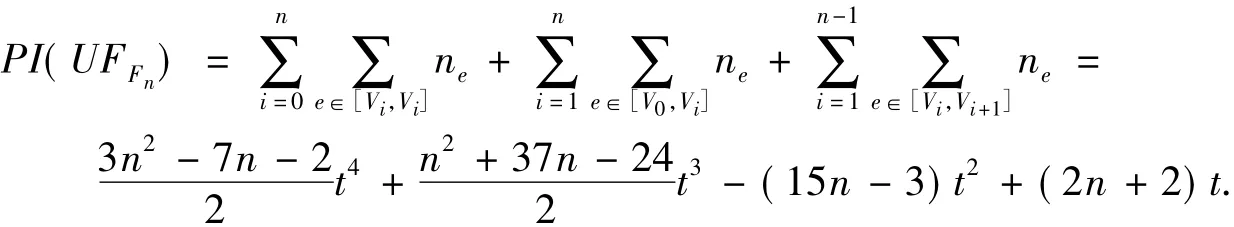
当n=3和n=4时，可用同样的方法证得定理2．定理2证毕．

［1］Khadikar P V，Karmarkar S，Agrawal V K．A novel PI index and its applications to QSPR/QSAR studies［J］．J Chem Inf Comput Sci，2001，41(4)：934-949．

［2］Hao Jianxiu．The PI index of gated amalgam［J］．Ars Combinatoria，2009，91：135-145．

［3］Hao Jianxiu．PI index of some simple pericondensed hexagonal systems［J］．Ars Combinatoria，2009，92：137-147．

［4］Bondy J A，Murty U S R．Graph theory with applications［M］．London：Macmillan Press Ltd，1976．

［5］许振宇，穆勇．扇与Halin图的一致膨胀图的关联色数［J］．济南大学学报：自然科学版，2006，20(3)：264-266．