等离子体模型中Poisson方程解的存在唯一性*
耿金波
(浙江师范大学数理与信息工程学院,浙江金华 321004)
0 引言
文献[1-4]对Euler-Poisson方程组的模型来源都有详细的介绍.本文考虑一维双极型Euler-Poisson方程组

式(1)中:x∈R3;u(x)∈R3;ρ是粒子密度;u为粒子速度;λ为德拜常数;C(x)为杂质的密度;Φ为电势.
彭跃军在文献[5]中利用Lax-Friedrichs格式和Godunov格式得到了方程组(1)的全局弱熵解的存在性;Natalini在文献[6]中得到了方程组(1)弱熵解的存在性;文献[7]研究了方程组含有松弛时间的双极型等熵Euler-Poisson方程组解的存在性及零松弛时间的极限.
本文运用压缩映像原理得到方程组(1)中的Poisson方程的解的存在性,使Euler-Poisson方程组化为双曲守恒律方程组,其主要结果为:
定理1 方程组(1)中的Poisson方程的边值问题

的解存在并且唯一.
1 引理
为了研究的方便,不妨假设方程组(1)中的λ=1,C(x)=1.
首先考虑下面的边值问题:

令
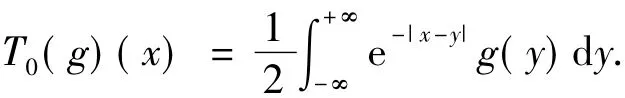
其中,g∈L1∩BV.可验证T0(g)(x)是问题(3)的解.为了得到本文结论,需要下面几个引理.
引理1 设g∈L1∩BV,则
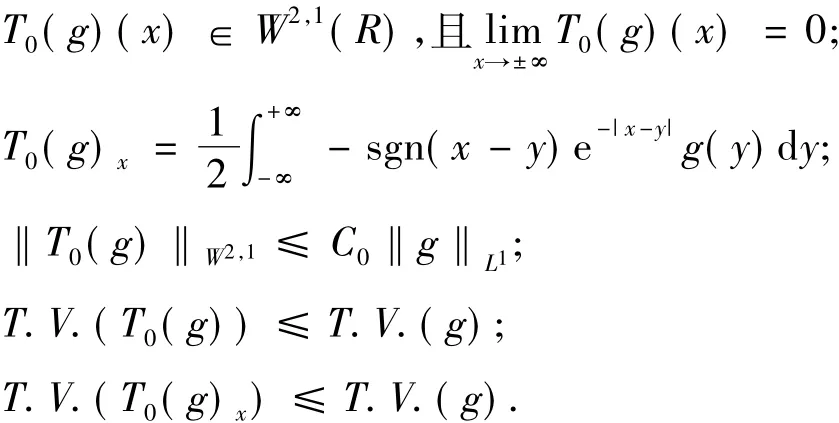
其中,常数C0与g无关.
证明 由g∈L1∩BV知

所以由控制收敛定理知

显然,

进而得到

由式(4)和式(5)可得引理1的结论.引理1证毕.
下面考虑非线性映射
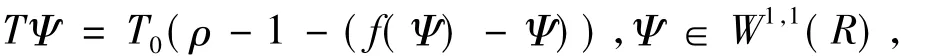
并记

其中,C0由引理1给出.
引理2 存在 δ0>0,使得当0 <δ<δ0时,TXδ⊆Xδ.
证明 任取Ψ∈Xδ,由嵌入定理[8]知:存在与Ψ无关的常数C1,满足
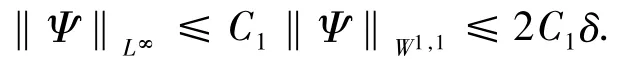
于是由引理1知

注意到f(Ψ)-Ψ=O(1)Ψ2,从而 limx→±∞T(Ψ)(x)=0.最后,在式(6)中取 δ充分小,使得 TXδ⊆Xδ.引理2证毕.
引理3 存在 δ0>0,使得当0 < δ< δ0时,T 在(Xδ,‖·‖W1,1)上为压缩映射.
证明 任取 Ψ1,Ψ2∈Xδ,有
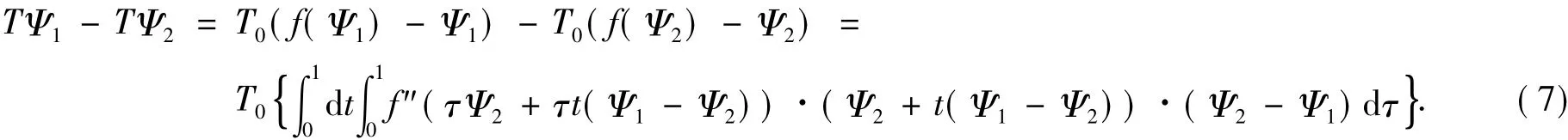
应用引理1,可得
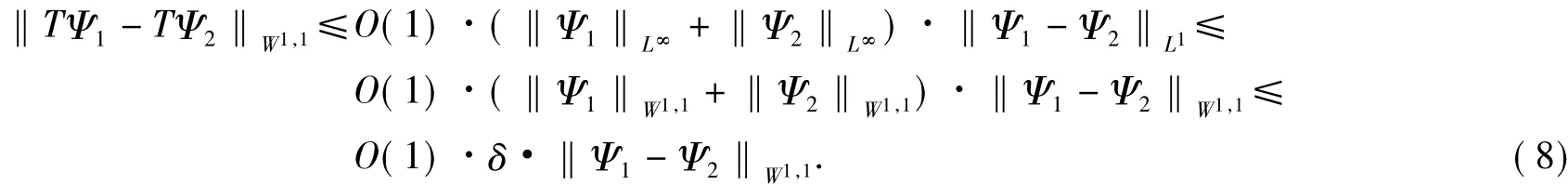
于是,在式(8)中取适当的δ,便可得到结论.引理3证毕.
大陆村到古辣镇上只用40分钟的车程,交通条件的改善,将为大陆村信息、物资的流通奠定良好的基础,便于人口的集聚,有利于旅游地产的发展。
引理4 存在 δ0>0,使得当0<δ<δ0时,存在唯一的 Φ ∈Xδ,有TΦ=Φ.进一步

证明 显然,由Banach压缩映像原理可以得到Φ的存在性.下面证明式(9)成立.由引理1可知
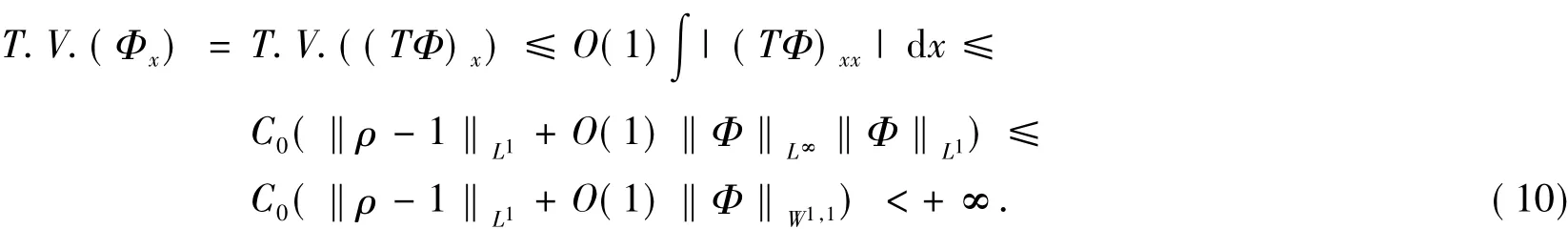
再次利用引理1得
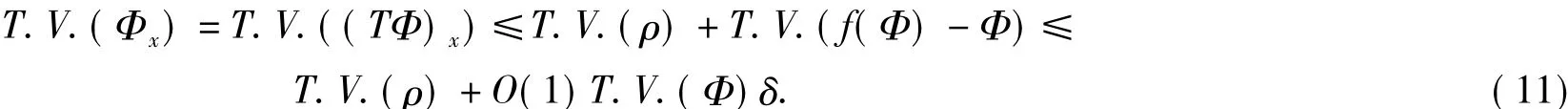
同理
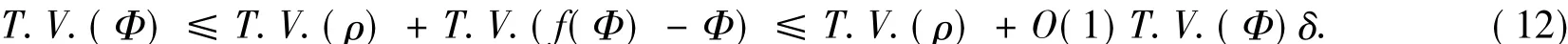
上述2个估计需要用到如下不等式:
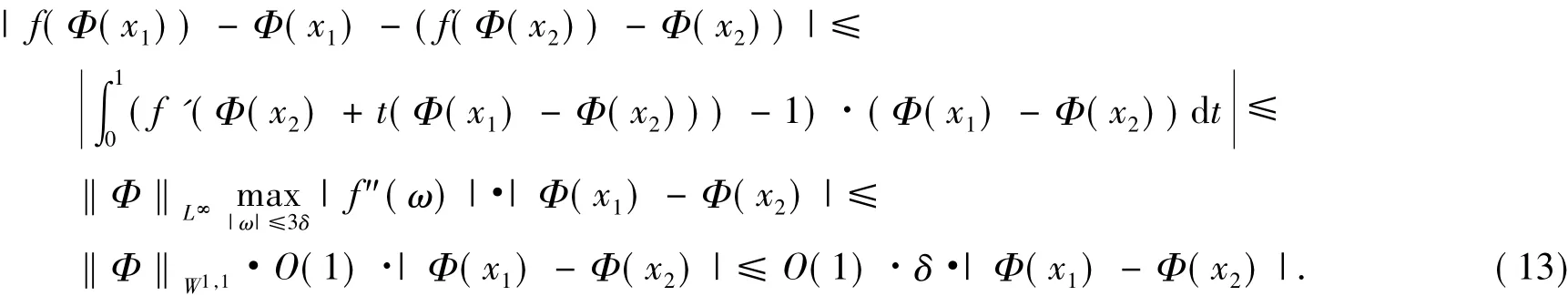
于是在式(11)和式(12)中取适当的δ,使得O(1)δ<1,得到
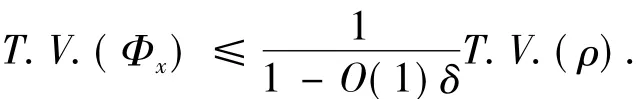
引理4证毕.
2 定理1的证明
由引理4知,Φ=TΦ,Φ∈Xδ给出了方程组

在Xδ上的唯一解.定理1证毕.
3 结语
定理1的证明是运用古典的压缩映像原理,对等离子体模型中的椭圆型方程解的存在性和唯一性进行了研究,它为进一步研究等离子体模型方程奠定了理论基础.
[1]李定,陈银华,马锦秀,等.等离子体物理学[M].北京:高等教育出版社,2006.
[2]王德焴,吴德金,黄光力.空间等离子体中的孤波[M].上海:上海科技教育出版社,2000.
[3]庄钊文,袁乃昌,刘少斌,等.等离子体隐身技术[M].北京:科学出版社,2004.
[4]Markowich P A,Ringhofer C A,Schmeiser C.Semiconductor equations[M].New York:Springer-Verlag,1990.
[5]Peng Yuejun.Convergence of the fractional step Lax-Friedrichs scheme and Godunov scheme for a nonlinear Euler-Poisson system[J].Nonlinear Analysis,2000,42(6):1033-1054.
[6]Natalini R.The bipolar hydrodynamic model for semiconductors and the drift-diffusion equations[J].Journal of Mathematical Analysis and Applications,1996,198(1):262-281.
[7]Jungel A,Peng Yuejun.Zero-relaxation-time limits in the hydrodynamic equations for plasmas revisited[J].Zeitschrift Für Angewandte Mathematik und Physik,2000,51(3):385-396.
[8]Adams R A.索伯列夫空间[M].叶其孝,译.北京:人民教育出版社,1981.

