杆式动能体侵彻多层靶板数值仿真*
赵汝岩,卢洪义,朱 敏
(海军航空工程学院,山东烟台 264001)
0 引言
杆式动能体对多层靶板的侵彻是侵彻力学中较为复杂的问题,普遍采用轻气炮、电磁炮和聚能射流三类方法对动能体进行加速,研究费用极高。随着科技的发展,有限元分析方法在侵彻力学的分析中得到了广泛的应用,龙源等人[1-3]对文献[4 -5]的模型采用文献[6]的本构方程对其侵彻过程及机理进行了分析研究,纪霞等人[7]对弹丸侵彻三层均质靶板进行数值模拟,分析了不同弹速、不同弹重产生的弹丸速度及加速度的变化,找到其中的变化规律;刘洋[8]利用显示动力学有限元程序ANSYS/LS-DYNA模拟着靶速度为2.0Ma和2.5Ma的战斗部对多层间隔靶板侵彻的过程。以上文献对侵彻初速小于2000m/s,靶板的厚度较小的情况进行模拟。文中借助ABAQUS软件,采用Lagrange法对高速杆式动能体无攻角正侵彻多层靶板的过程进行数值模拟,研究不同初速的动能体侵彻各层靶板后的剩余长度以及剩余速度,为高速动能体侵彻多层靶板的工程应用提供参考。
1 数值计算
1.1 物理模型
动能体和多层靶板看作是均匀连续介质,认为整个侵彻过程是绝热的,不计空气阻力,不考虑重力作用。由于杆式动能体和多层靶板在结构上的对称性,取1/2实体建立模型,并在对称面上施加对称约束,对各层靶板的侧边施加边界条件,模拟各层靶板四周被固定的情况。体靶的几何模型如图1,图中序号1-9代表各层靶板,其中第2层、第4~第8层靶板厚度为L,第1层靶板厚度为10L,第3层靶板厚度为6L,第9层靶板厚度为20L。各层靶板之间的距离为40L。动能体的尺寸为Φ5L×100L。

图1 杆式动能体侵彻多层靶板物理模型
1.2 材料模型
1.2.1 材料属性
动能体和靶体采用相同的材料,为某型钨合金材料,其弹性模量 E=345GPa,泊松比 v=0.22,密度ρ=18000kg/m3。
1.2.2 屈服准则
动能体和靶板仿真模型材料采用具有弹塑性属性的Johnson-Cook模型。其屈服函数为:
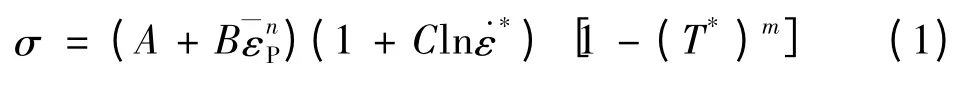
式中:A、B、n、C、m为材料参数;其中A=1.093GPa,B=1.278GPa,n=0.42,C=0.0188为有效塑性应变率;˙ε0为参考塑性应变率,一般取˙ε0=1s-1;T*=(1-Tr)/(Tm-Tr),Tr为参考温度;Tm为熔点温度。
1.2.3 损伤准则
考虑应力三轴度、应变率和温度效应,并通过累积损伤的概念考虑变形路径的影响,定义单元损伤:

式中:D为损伤参数,在0~1之间变化,初始时D=0,当D=1.0时材料失效;Δεp为一个时间步的塑性应变增量;εf为当前时间步的应变状态、应变率和温度下的破坏应变,其表达式为:
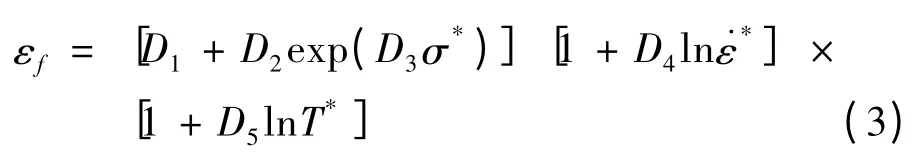
式中:D1~ D5为材料参数,大小分别为0.07,1.73,- 0.54,- 0.012,0;σ*=p/σeff为应力状态参数,其中p为压力,σeff为等效应力。
2 仿真结果及分析
2.1 杆式动能体侵彻多层靶板历程图
图2为动能体以2000m/s的速度无攻角正侵彻多层靶板的历程图。从图中可以看出当t=72μs时处于杆式动能体侵彻第一层靶板的冲塞阶段,由于受压缩应力波作用,在第一层靶板背面出现鼓包(见图2(a));当t=240μs时,动能体已经穿透第一层10L的靶板且即将撞击第二层厚度为L的靶板,但是第一层靶板的碎片已经撞击到第二层靶板上,使靶板产生塑性应变;而当t=600μs时,动能体已经穿透第二层靶板,而靶板碎片已经作用于6L的第三层靶板(见图2(c));t=960μs时,动能体穿透第五层靶板;t=1460μs时,动能体穿透第八层靶板,而此时第三层靶板在被穿透过程中具有的动能继续破坏靶板,使靶板产生更多的碎片(见图2(e));t=1730μs时,动能体穿透最后一层靶板。
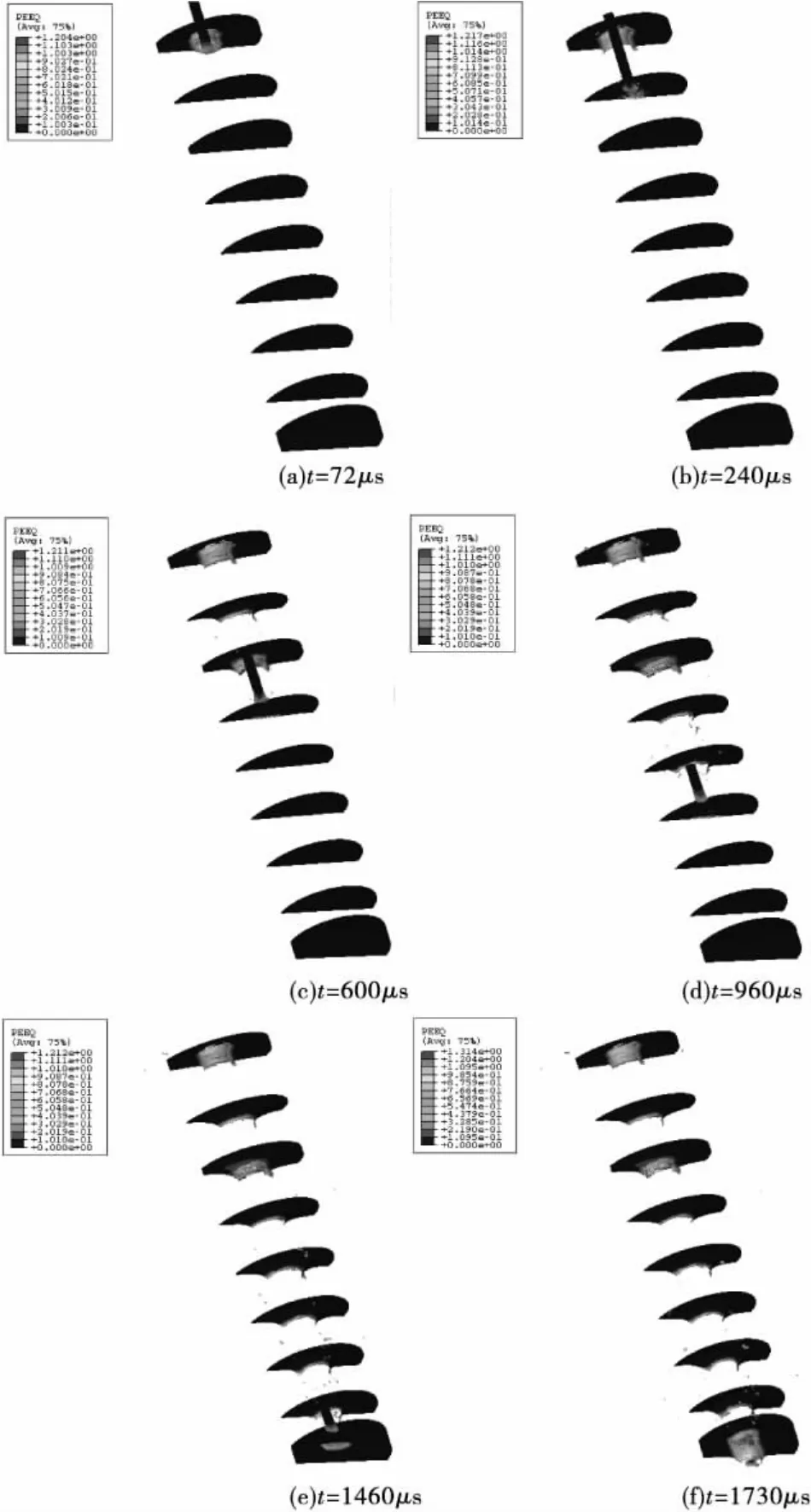
图2 动能体(Φ5L×100L)侵彻多层靶板历程图
2.2 动能体破损变形分析
图3 为杆式动能体侵彻过程中的外形图。由于靶板的可变形性以及动能体与每层靶板撞击端面中心和边缘处的塑性变形不同步导致在动能体撞击端面出现一圆形凸台;随着侵彻过程的进行,动能体的撞击端墩粗面积也相应增加,呈现蘑菇头形状,并在一定速度下动能体撞击端边缘出现破坏失效。仿真结果与参考文献[9]中的残余动能体外形(见图4)类似。

图3 侵彻过程动能体外形图

图4 试验弹孔纵剖面和残余弹芯
图5 为动能体以4000m/s的速度撞击第一层靶板时端面中心和边缘处两点的塑性变形历程。中心部位单元的塑性应变在撞击初期增长迅速,在0.5μs左右该单元失效,在此之后的应变均不再发展。而边缘部位单元的应变继续持续增长,直到在1μs左右,旁边单元失效卸载。由于端面中心和边缘处塑性变形的不同导致动能体撞击端呈现蘑菇头状。
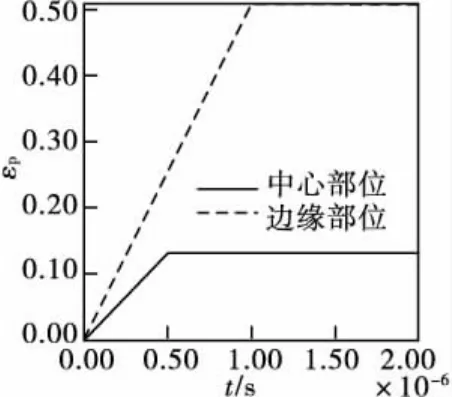
图5 动能体撞击端面的塑性变形
图6 (a)是不同长径比的动能体以2000m/s的速度侵彻各层靶板后的剩余长度变化图,而图6(b)是不同初速的动能体侵彻各层靶板后的剩余长度变化图,图中横坐标表示动能体所要侵彻的靶板的层数。在其他条件不变的情况下,通过图6(a)可以看出,长径比较大,动能杆侵彻靶板的层数也多;通过图6(b)可以看出随着初速的增加,穿透每层靶板后相对剩余长度(即弹丸剩余长度Lr与原始长度L0的比值)却在减少,而当动能体以4000m/s的速度侵彻最后一层靶板的过程中,动能体已经完全破碎。这意味着初速更高的动能体穿透相同的间隔靶板侵蚀现象更加严重,这无疑降低动能体的侵彻后效。
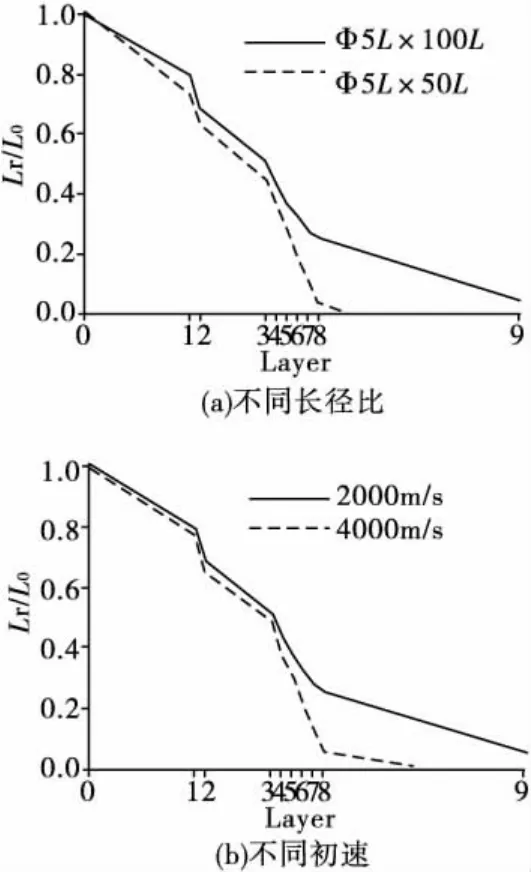
图6 动能体侵彻各层靶板的剩余长度变化图
2.3 动能体速度曲线分析
图7 和图8为初速分别为2000m/s和4000m/s的动能体侵砌多层靶板过程中动能体的速度变化曲线图。通过图7和图8可以看出,不同初速的动能体在侵彻前八层靶板的过程中动能体的速度震荡变化,这是由于侵彻每层靶板都要经历开孔、侵彻、充塞3个阶段,这个过程中动能体动能急剧转化为形成塞块所作的功,速度迅速下降;塞块形成后,靶板抗力迅速减少,此时动能体内各种激波的复杂作用使动能体速度有所回升,随后动能体对靶板的扩孔破坏作用又使其动能转化为塞块的动能和破坏靶板所需的功,动能体速度又一次快速下降,动能体对每层靶板的侵彻结束,此时动能体内各种激波的作用再次使动能体速度有所回升,这个过程持续到动能体侵彻下一层靶板。
当动能体侵彻底层靶板前,动能体速度缓慢下降,在侵彻底层靶板过程中,动能体速度迅速降低。这是由于在动能体侵彻前几层靶板过程中,动能体破坏比较严重,动能体在侵彻最后一层靶板前相对剩余长度较小(见图6),因此在侵彻同样材料的靶板时速度降低较快。

图7 动能体速度变化曲线图(2000m/s)
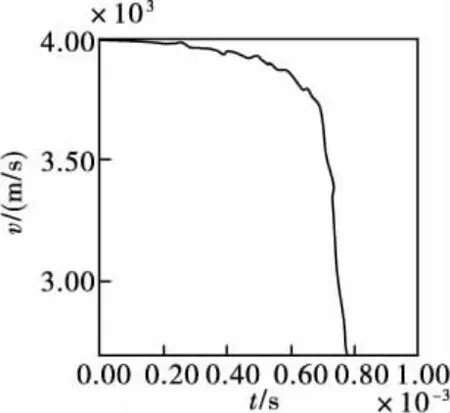
图8 动能体速度变化曲线图(4000m/s)
3 结论
通过对动能体以不同速度无攻角正侵彻多层靶板的仿真结果可以分析得出:
1)动能体侵彻多层靶板的过程中,由于动能体的磨损导致动能体速度降低的程度先小后大,直至停止;
2)初速高的动能体穿透相同的间隔靶板后侵蚀现象更加严重,这将降低动能体的侵彻后效,因此选用速度更高动能体侵彻多层靶板效果未必最佳。模拟的结果对于动能体侵彻多层靶板具有一定的参考价值。
[1]岳小兵,龙源,方向,等.高速模拟钢质弹丸侵彻多层靶仿真[J].解放军理工大学学报:自然科学版,2003,4(4):40-44.
[2]龙源,岳小兵,周翔,等.高速钢弹对多层大间隔金属靶的侵彻特性研究[J].南京理工大学学报,2004,28(4):369-374.
[3]谢文,龙源,岳小兵.模拟爆炸成形弹丸对大间隔靶的侵彻实验研究[J].兵工学报,2003,24(3):392-395.
[4]Rondot F.Performance of tantalus EFP simulants[C]//17 th International Symposius on Ballistics,Midrand:S African Ballistics Org,1998:225 -232.
[5]Rondot F.Performance of aerodynamically optimized EFP simulants[C]//17th International Symposius on Ballistics,Midrand:S African Ballistics Org,1998:81-88.
[6]Gordon R J ,Willam H C.Fracture characteristic of three metals subjected to various strains,strain rates,temperatures and pressures[J].Engineering Fracture Mechanics,1985,21(1):31-48.
[7]纪霞,王利.弹丸侵彻多层靶板数值分析[J].探测与控制学报,2006,28(2):42 -45.
[8]刘洋,姚江涛,李国林,等.用数值模拟法研究战斗部侵彻多层间隔靶[J].海军航空工程学院学报,2009,24(2):144-151.
[9]荣光,黄德武.钨纤维复合材料穿甲弹芯侵彻时的自锐现象[J].爆炸与冲击,2009,29(4):351-355.

