中小型固体火箭发动机喷管扩张比寻优算法*
张久云,杜国秀,齐子凤
(中船重工第710研究所,湖北宜昌 443003)
0 引言
固体发动机作为动力推进装置在各类箭弹中被广泛应用,产品研制阶段,总体对动力分系统提出设计要求,包括总冲量、工作时间及质量与尺寸限制等。发动机设计的目标就是根据设计输入进行初步设计、迭代优化,设计一型高质量的发动机,使自身性能达到最优。
应用发动机设计程序与方法,依据箭弹总体要求经过初步设计之后,发动机部分设计参数可得以固化,如燃烧室的工作压强和内径、喷喉尺寸、装药类型等。然而喷管扩张比等参数在此阶段却无法确定,由于没有现成的数学模型和具体可用的、“性价比”较高的算法,目前对扩张比的选取往往凭设计经验或参考同类产品在4~10之间选取,具有随意性和盲目性。
扩张比等参数对发动机的整体性能又有重要影响,因此设计发动机时,喷管扩张比究竟如何计算和确定,需进行优化设计。
1 算法数学模型
发动机设计涉及诸多参数,关系复杂,其优化设计是一个有约束的非线性规划问题,其数学描述是:求设计变量 X=(x1,x2,…,xn)T,使得目标函数F(X)为最大。
质量比冲(或称冲质比)是衡量发动机性能的重要指标,因此将冲质比设为目标函数,通过对发动机喷管扩张比进行优化设计而使发动机冲质比最大。
由理论分析和工程试验可知,在设计中小型固体发动机时,喷管采用欠膨胀设计。在此情况下,若喷管扩张比增大,则喷管扩张段质量增加。但由于推进剂比冲随之增大,在总冲不变的前提下,发动机装药量减少。同时因装药体积减小使燃烧室壳体质量随之降低,因此,若同时考虑装药比冲和结构重量的因素,必然存在一个最优膨胀比ε*,能使发动机冲质比最大。或者说,在总冲一定时,ε*能使发动机质量最小。
据此建立了数学模型和优选算法,发动机设计过程中,若确定部分设计参数之后,应用此算法即可求得最优扩张比ε*。
发动机冲质比为:
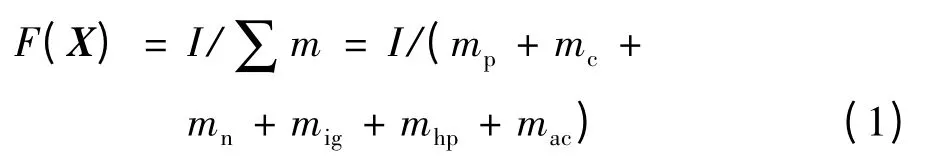
式中:mp表示推进剂质量;mc表示燃烧室质量;mn表示喷管质量;mig表示点火具质量;mhp表示封头等质量;mac表示挡药板等附件质量[1]。
一般情况下,总冲由总体根据箭弹应用给定。按固体火箭发动机总体设计方法经过一轮初步设计后,mig、mhp、mac三者之值基本确定,在后续优化设计过程中变化甚微,可按固定值处理,发动机总质量仅随着燃烧室、喷管和推进剂三者质量改变而变动。下文将建立数学模型,直接表示三者质量与喷管扩张比的函数关系,继而用复合形法(此时参量转化为一维)寻求最优扩张比值。
1.1 喷管质量模型
喷管扩张比的大小影响着发动机的比冲、结构质量和总体性能,因此是发动机的一个重要设计参量。
新闻摄影是新闻报道的重要手段之一,通过对新闻事件及信息的可视性传播,提升观众对新闻节目的参与感。就目前来看,新闻摄影具有以下特征。
中小型固体发动机多采用锥形直喷管或采用多段二次、三次曲线拟合的劳(Lao)喷管[2]。为便于研究,文中将喷管总重量细分为三部分:喷管收敛段质量mnb,喷管喉部过渡段质量mnt,喷管扩张段质量mna。
若燃烧室压强pc、喷喉直径dt和喷管基本结构形式在初步设计和依照总体要求确定之后,mnb、mnt可视为定值。喷管质量随着扩张比的变化而变化,建立喷管扩张段质量模型,扩张段质量表示为扩张比的函数(以扩张段起始截面与喷管轴线为基准建立R-X坐标系,如图1,根据内型面曲线方程可知扩张段内任意截面上的半径尺寸R=R(x))。

图1 喷管扩张段结构示意
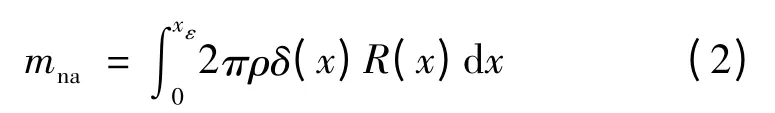
现以中小型发动机和助推器常采用的锥形直喷管为例示意计算的方法。
在锥形直喷管设计中,扩张段采用渐变式壁厚设计。喷管扩张段入口和出口的厚度δ根据所选材料、热防护、压力载荷、热载荷因素进行工程估算,并认为厚度从入口到出口均匀变化。将扩张段沿轴向进行微分,每一小段可视为圆环。
则锥型喷管扩张段质量关系式为:

1.2 装药质量模型
喷管扩张比的变化不仅引起其扩张段质量变化,由于改变了喷管性能、膨胀比和出口压力,对推进剂的比冲和推力系数也产生影响。由喷管理论可知,pe/pc是ε的单值函数,即
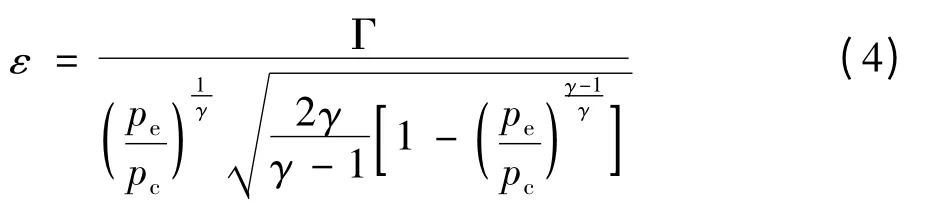
式中:γ为燃气比热比;Γ是比热比的函数。
若将某一定值赋给扩张比,用数值计算方法中的二分法编程计算或直接以Matlab符号命令fsolve即可解非线性方程(4)求取值,即pe/pc,由于低空中小型发动机扩张比一般小于10,数值计算时,可将求解域设为(0.01,0.564)。继而由式(5)即可计算该扩张比下对应的装药质量。
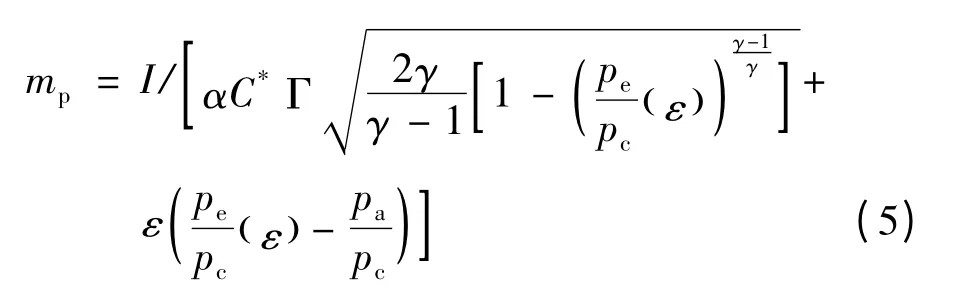
式中:α表示喷管效率,是扩张比和扩张角的函数,对于所选定的推进剂,γ为已知量,pa≈0.1MPa,故在此情况下,装药质量是扩张比函数,mp=mp(ε)。
1.3 燃烧室质量模型
燃烧室的质量细分为固定质量mfix和随动质量malt两部分。
初步设计确定了燃烧室压强和直径,燃烧室有一部分结构(如与封头或其它部件间的连结或支撑结构)随之基本确定,这部分结构的质量即为固定质量mfix。同时燃烧室作为容纳装药的壳体,若推进剂体积发生变化,则其容纳药柱的那部分结构的质量也随之改变,此处称之为随动质量。
参照金属筒体壁厚的计算方法,由材料力学中的最大应力强度理论,随动质量可处理为装药长度(Lp)的函数。
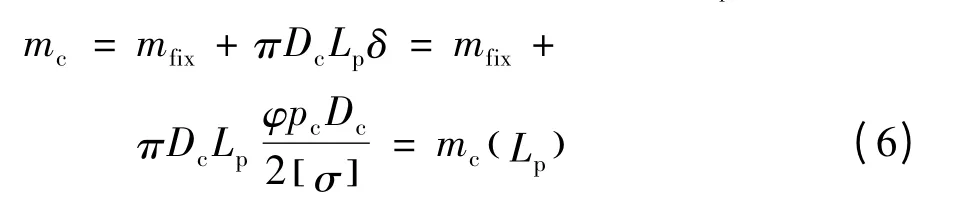
在确定pc、dt情况下,对于选定推进剂,由内弹道计算公式可知,须将燃喉比KN值固定,即装药燃面不因装药量的变化而改变。在此前提下,可根据发动机内弹道各参数计算式获得方程组(7)。
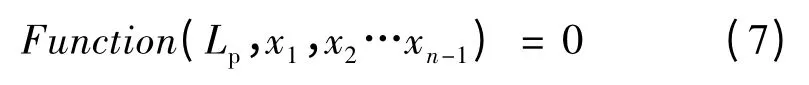
现以中近程火箭弹常用的管型装药为例,示意计算Lp的方法。
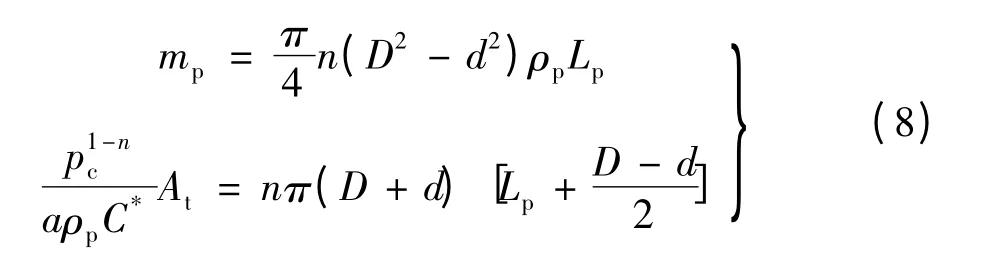
上式中,装药质量由式(5)已求,经初步设计已经确定装药形式和燃烧室直径等参数,则装药根数和药柱外径为已知值。方程组(8)实为药柱长度Lp和药柱内径d的二元二次非线性方程组,此方程组是闭合的。用牛顿迭代法编程计算 Function[d,Lp]=Newton_Lp(f,[d0,Lp0],e)或 Matlab 的 符 号 命 令fsolve求取药柱长度Lp。
1.4 最佳扩张比寻优算法及流程
至此,在发动机经过初步设计确定部分参数之后,设定一扩张比ε,即可求得相应发动机可变质量,进而计算得发动机冲质比。发动机可变质量最小,发动机冲质比即最大值对应的ε就是发动机设计中所寻求的最优扩张比ε*。接下来介绍文中选用复合形法求取ε*的算法流程。
以ε=ε0为计算起始点,由前文的数学模型和式(1)计算对应冲质比F(ε),然后以同样的流程计算ε=ε+Δ对应的冲质比F(ε+Δ),Δ为循环计算递加步长,一般而言,Δ =0.01能满足绝大部分精度要求,并比较二者大小,若F(ε+Δ)大于F(ε),则继续之前的程序,直至F(ε+Δ)< F(ε),则当前ε即为所求ε*。
文中研究时应用面向对象程序设计方法,利用C++语言进行程序设计。程序流程图见图2。
流程图中,数据框中表示的根据箭弹总体要求或约束和发动机初步设计所得参数包括发动机设计总冲、燃烧室外径和平衡压强、装药根数和药柱外径、喷管扩张比、喷喉直径、装药密度、燃气比热比、特征速度、燃烧室材料密度等等。
2 工程算例
某型火箭弹发动机根据总体要求经过第一轮发动机设计,所得参数如下。
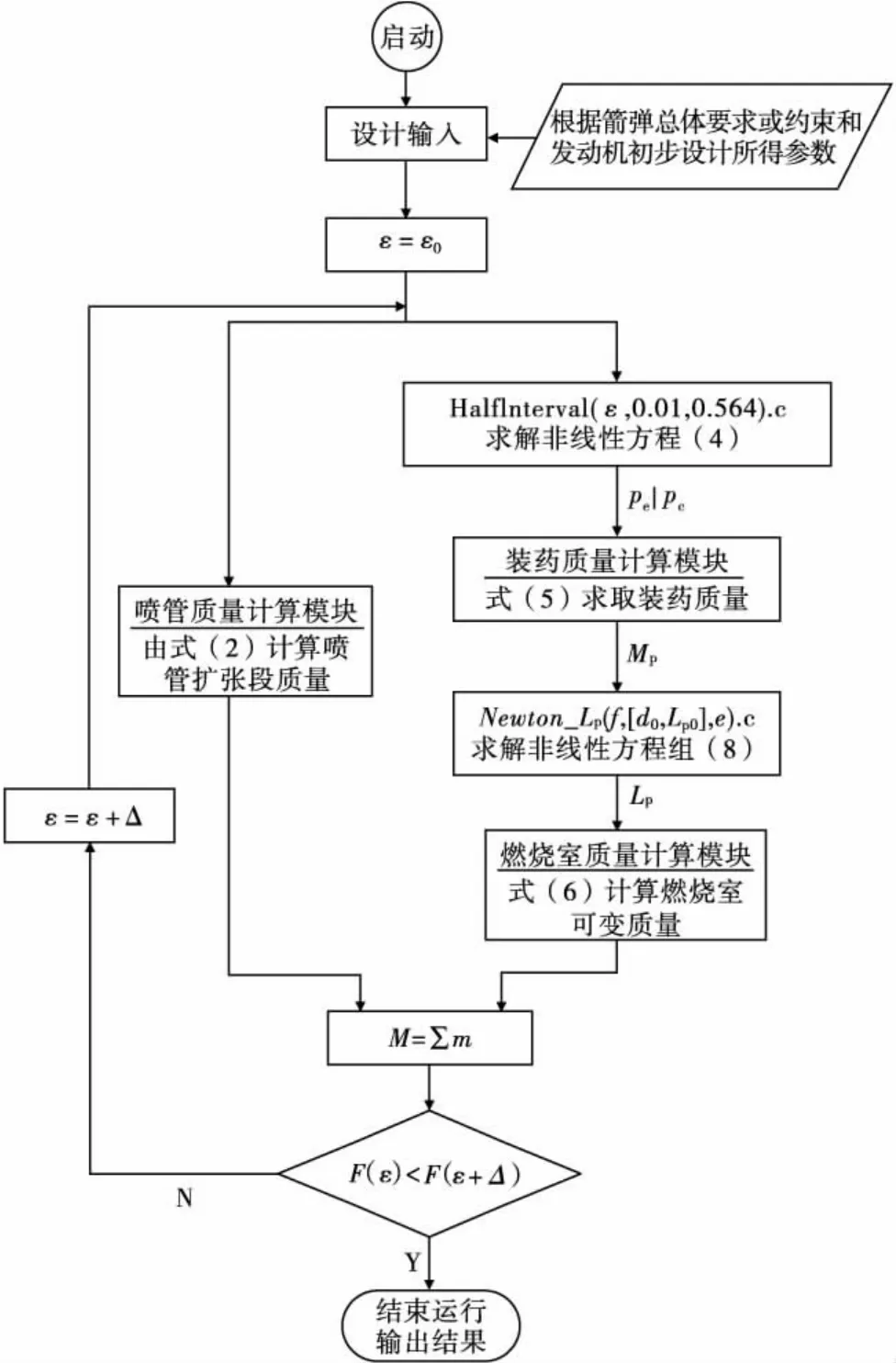
图2 优化算法流程图
发动机总冲要求4500N·s;初步方案所选用推进剂,20℃ 燃速公式为 0.3494p0.285cm/s,特征速度为1350m/s,密度为1650kg/m3;燃烧室平衡压强为10MPa;根据整弹尺寸确定燃烧室直径为131.2;装药类型为19根管状装药,药柱外径26.5(根据燃烧室外径和装药根数确定);喷管喉部直径确定为28.5,扩张半角为13.5°,发动机壳体采用金属材料;若在设计时,将扩张比初定为4,此时冲质比为746.2。
根据文中的数学模型和优选算法,以程序流程图2用C语言编写源代码,输入初始参数后以ε0=1为计算初值,运行程序,结果输出该发动机最优扩张比ε*=5.67,发动机目标函数质量比冲达到759.3。
3 小结
1)文中提出一种基于发动机质量比冲最大原则的喷管扩张比寻优算法,其数学模型和算法合理可行,可以快速获取喷管最佳扩张比,为喷管扩张比的选择提供了科学依据。
2)该算法尤其适用于中小型固体发动机设计时,确定了燃烧室外径尺寸和平衡压强之后对喷管扩张比的最佳值寻优。是对目前发动机优化设计方法的完善和补充,也为后续的研究提供了方法和思路。
[1]杨月诚.火箭发动机理论基础[M].西安:西北工业大学出版社,2010.
[2]何景轩,田维平,何国强,等.基于遗传算法的固体火箭发动机参数优化设计[J].固体火箭技术,2004,27(4):250-254.
[3]何景轩,甘晓松,乐发仁,等.固体火箭发动机燃烧室压强及喷管扩张比优化设计[J].固体火箭技术,2003,26(4):12-13.
[4]瓯海英,张为华,解红雨,等.基于图形变形法的固体火箭发动机优化设计[J].推进技术,2006,27(3):201-204,207.
[5]李晓斌,张为华,王中伟.固体火箭发动机装药不确定性优化设计[J].固体火箭技术,2006,29(4):269-273.

