基于某种无陀螺惯性测量单元的安装误差补偿*

刘 涛，赵国荣，徐珂文

(海军航空工程学院，山东烟台 264001)

0 引言

无陀螺捷联惯导系统(gyroscope free strap-down inertial navigation system)是仅利用线加速度计来完成惯性测量与导航任务的导航系统，避免了使用工艺复杂的陀螺仪，具有低成本、低功耗、长寿命和高可靠性等优点，特别适用于大动态范围、导航时间短的载体。系统的运动解算全部来源于加速度计的输出，理论分析和试验表明，加速度计的安装误差对系统精度的影响十分显著，不容忽视[1－4]。文中针对一种具有代表性的九加速度计配置方案，分析了加速度计的安装误差，研究了实验标定方法和误差的补偿方案，并通过仿真验证了其有效性。

1 加速度计输出模型

由加速度计的比力方程:

得到加速度计位置的3个轴向比力向量fb为:

其中:

设加速度计的敏感方向为θ，则加速度计的输出为:

2 配置方案及角速度解算方法

图1为一种具有一定代表性的九加速度计配置方案，其加速度计的位置矩阵和方向矩阵分别为:

其中，l为非原点处加速度计到原点的距离，由式(1)得到加速度计输出方程为:

文献[5－6]分别运用开方法、辅助算法、Kalman滤波和智能加权算法进行角速度的解算，其中智能加权算法的解算精度最高。但在解算过程中都未考虑加速度计的安装误差，而将加速度计安装在载体上，不可避免的存在安装误差，包括位置误差和方向误差，特别是本方案中需要将多个加速度计安装在同一个理论点上。

3 安装方向误差分析及标定

方向误差可以通过坐标旋转来表示，如图2所示，θ和θr分别表示加速度计的理想和实际安装方向，Δα和Δβ为方向误差角[7]，其正负符号规定为:逆时针旋转为正，顺时针旋转为负，则:

其中C1、C2分别为两次坐标旋转的坐标变换阵。

方向误差向量:

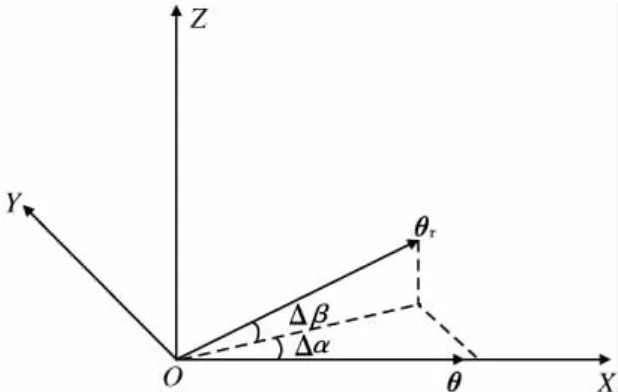
图2 安装方向误差示意图

其中I为单位阵。

标定方案:将惯性系统放置在旋转台上，分别以oxy、oyz、oxz为水平面，进行静态条件(线运动和角运动都为0)实验，得到加速度计的输出值A(mn)ri，m=1，2或3，分别表示以oxy、oyz、oxz为水平面，n=1，表示转台静态条件，i代表加速度计的序号。此时加速度计的输出值为重力加速度在其敏感方向的分量，即:

由3次实验结果得到加速度计的方向误差角，从而得到方向误差向量。以加速度计1为例求解方向误差向量 Δ θ1。

得到:

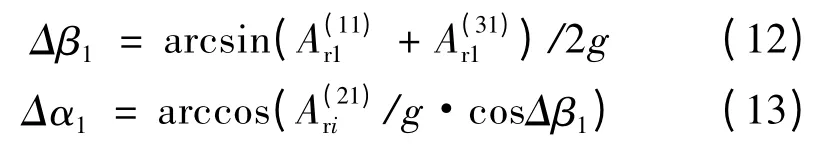
由式(10)得:

表1列出了各加速度计方向误差角的计算公式，表2列出了方向误差向量。

表1 各加速度计的方向误差角计算公式

表2 各加速度计的方向误差向量

4 安装位置误差分析及标定

4.1 安装位置误差标定方案

加速度计的安装位置误差可由其坐标投影来表示，如图3，以加速度计2为例，P点为加速度计的理想安装位置，P'点为加速度计的实际安装位置，Δl为安装位置误差向量，其在各坐标轴的投影为[Δlx，Δly，Δlz]。

图3 安装位置误差示意图

标定方案:将惯性系统放置在旋转台上，分别以oxy、oyz、oxz为水平面，进行匀速旋转(ω = ω0)条件下的实验，得到加速度计的输出值A(mn)ri，其中n=2，表示转台匀速条件。由式(3)可以得到匀速转动时的加速度计输出为:

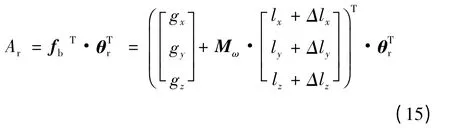
式中采用方向误差实验中得到的实际敏感方向，根据3次测量值就可以得到三元方程组 f(Δlx，Δly，Δlz)，从而计算出每个加速度计的安装位置误差。

4.2 方案改进

为了提高标定精度，减小随机误差的影响，实验中对旋转台转速ω0进行j次取值，这样每个加速度计就可以得到m个实验输出值(m=3j)，得到三元方程组 f(Δlx，Δly，Δlz)，从而进行 Δlx、Δly、Δlz的求解。

对式(15)进行分离 Δlx、Δly、Δlz操作:

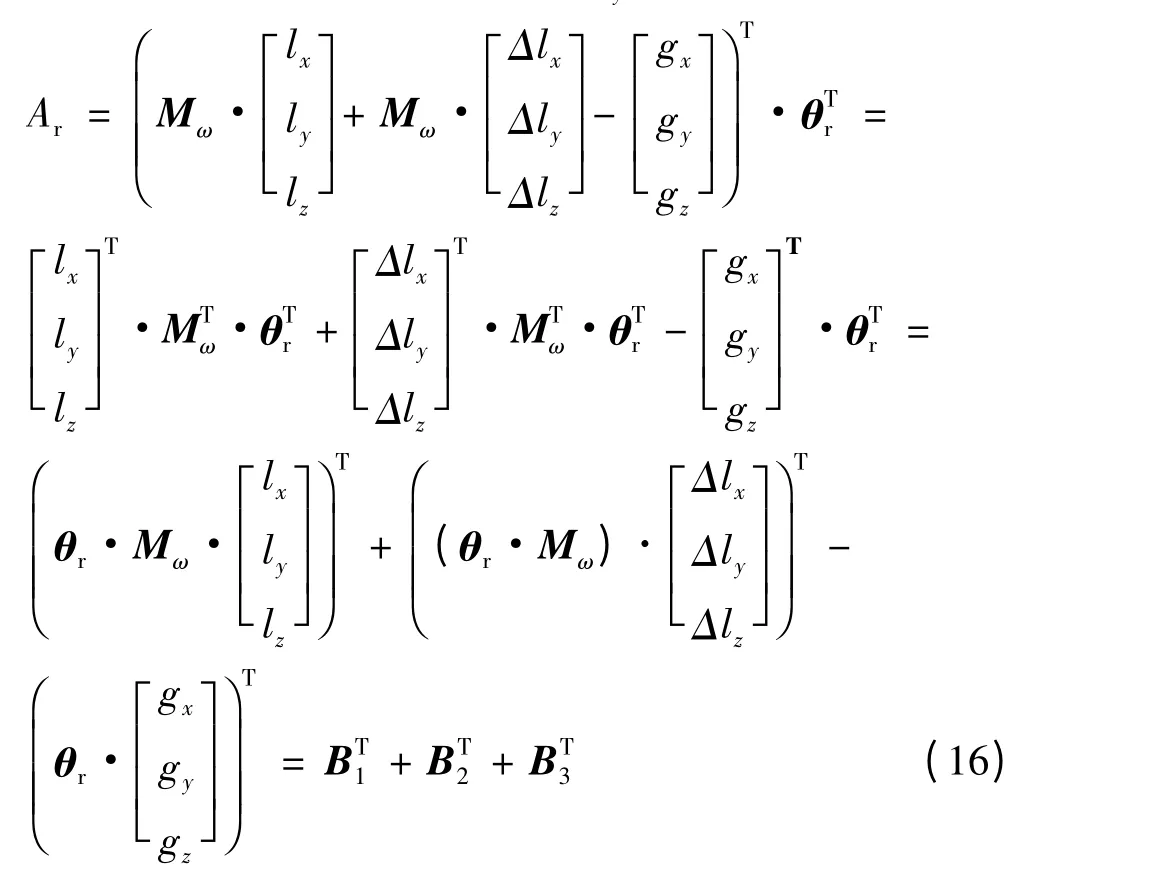
其中:

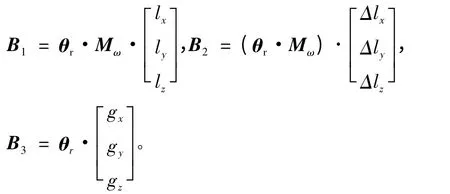
由于B1、B2、B3均为一维矩阵，即为数值形式，其转置形式不变，因此得到:

其中:

由m个这样的方程组成的方程组为:

即:

其中ωm为第m次实验转台的转速。

可以看出，矩阵方程(20)的独立方程个数m ＞3，属于超定矩阵方程。本方程的形式满足线性方程Ax=b，而数据向量 b含有观测数据向量，存在测量误差，并且其和系数矩阵A都包含了已经计算得到的加速度计敏感实际方向θr，也存在一定的计算误差，可以作为噪声项，且两者不相关。求解这种系数矩阵A和数据向量b都存在误差的超定方程的最佳方法是总体最小二乘法。

4.3 总体最小二乘法

对于超定方程Ax=b，总体最小二乘法不仅用扰动向量e去干扰数据向量b，而且用扰动矩阵E同时干扰数据矩阵A，以便校正在A和b二者内存在的扰动。考虑矩阵方程:

可以写为:

其中，增广矩阵 B = [－b，A]，扰动矩阵 D=[－ e，E]。

对增广矩阵B进行奇异值分解，令:

此时，如果增广矩阵B的最小奇异值多重(往往表现为最后几个奇异值重复或者非常接近)，假设有n+1－p个最小奇异值(p≤n+1)，则矩阵方程会有p个总体最小二乘解。然而，可以找出在某种意义下唯一的最小二乘解，包括最小范数解和最优最小二乘近似解。

文中希望得到的是矩阵方程式(20)的所有未知参量，即最小范数解:

其中，向量v1是矩阵V列分块形式的第一行，具体求解步骤见文献[8]。

5 安装误差补偿

由于加速度计安装误差的存在，不能将实际的输出Ar代入公式解算角速度，而应该进行补偿，消除其中的安装误差:

由式(3)和式(15)得到:ΔA=Ar－ A=

补偿过程中，ΔA中所涉及的V、˙V、ω、˙ω均采用上一时刻的解算值。图4为补偿方案的流程图。

图4 补偿方案示意图

6 算例仿真

借 助某型导弹前40s的飞行数据进行仿真实验，图 5为其飞行轨迹 图。 设加速度计的精度为5×10－6g，随机噪声为10－5g，仿真步长为0.01s，l=0.3m，加速度计的位置误差矩阵和方向误差矩阵为:

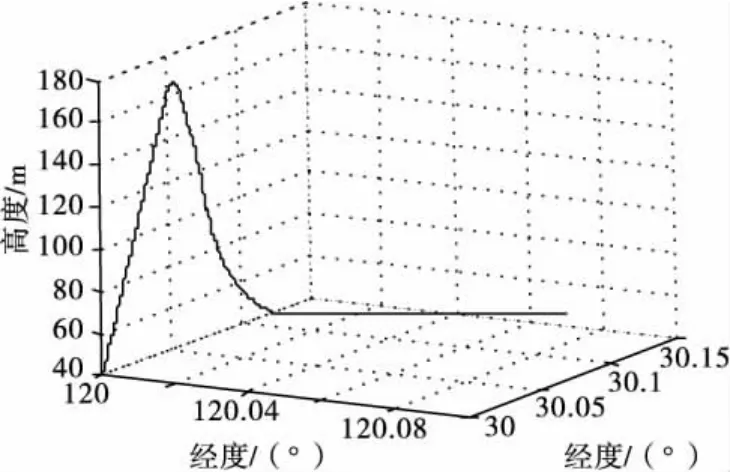
图5 某型导弹运行轨迹

利用智能加权算法对角速度进行解算，以x方向为例，图6分别给出了对安装误差补偿前后的角速度解算误差曲线，表3为解算误差数据，图7为安装误差补偿前后的东向导航误差。

图6 安装误差补偿结果对比图

从仿真结果可以看出，如果不对安装误差进行补偿，角速度解算误差和导航误差较大。利用文中的补偿方案，x轴向角速度解算精度提高明显，而东向导航误差最大值也由3.2987m减小到了0.3454m，效果显著。

图7 东向导航误差

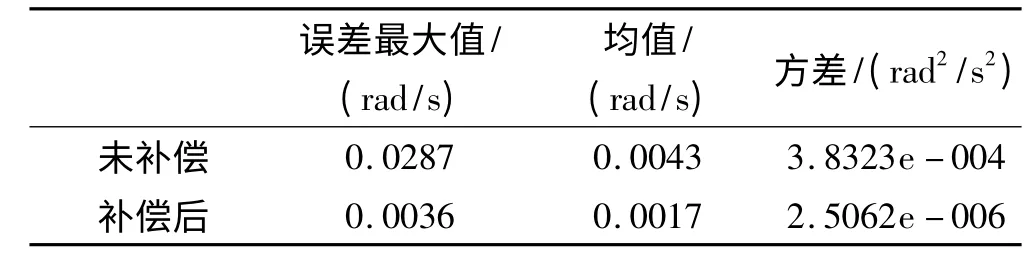
表3 安装误差补偿前后误差数据

7 结论

加速度计的安装误差对无陀螺惯性测量系统精度的影响十分显著，不容忽视，利用文中的标定和补偿方案，实现简单，可以有效的提高角速度的解算精度和系统的导航精度。

[1]马澍田，陈世有，李艳梅.无陀螺捷联惯导系统[J].航空学报，1997，18(4):484－488.

[2]T L Chen.Design and analysis of a fault-tolerant coplanar gyro free inertial measurement unit[J].Journal of Micro-electromechanical Systems，2008，17(1):201 －212.

[3]Kourosh Parsa，TyA Lasky.Design and implementation of a mechatronic all-accelerometer inertial measurement unit[J].ASME Transactions on Mechatronics，2007，12(6):640－650.

[4]Chin-Woo Tan，Sungsu Park.Design of accelerometer-based inertial navigation systems[J].IEEE Transcations on Instrumentation and Measurement，2005， 54(6):2520－2530

[5]赵国荣，陈穆清.一种用于九加速度计GFSINS的姿态角速度辅助算法[J].系统仿真学报，2007，19(14):3350－3353.

[6]刘涛，赵国荣，潘爽.无陀螺捷联惯导系统角速度解算的新方法[J]系统工程与电子技术，2010，32(1):22－25.

[7]汪小娜，王树宗，朱华兵.无陀螺捷联惯导系统加速度计安装误差研究[J].兵工学报，2008，29(2):159－163.

[8]张贤达.矩阵分析与应用[M].北京:清华大学出版社，2004:401－436.