直接基于位移的抗震设计理论及应用

刘鹏飞章德华

（1.铜陵学院，安徽 铜陵 244000；2.芜湖新裕建筑工程设计有限责任公司，安徽 芜湖2 41000）

1.引言

试验研究表明，建筑结构在各阶段的性能与其变形指标有较好的相关性，即结构性能与其变形指标之间可建立定量关系，但与力之间没有很好的相关性。另外，建筑结构在大震作用下倒塌的主要原因，是由于其变形能力和耗能能力不足所造成的。因此，在建筑结构设计初期，以变形（位移）作为设计变量，设计者可以控制结构在地震作用下的行为。

结构的位移控制抗震设计方法长期以来一直存在于工程结构的概念设计阶段，比如高层建筑结构体系的选择往往是以变形(或刚度)作为主要控制参数。对这种设计概念，Sozen于1981年首先进行了系统的阐述，他认为既然结构的层间位移是直接影响结构及非结构构件损伤的主要参数，设计人员在进行抗震设计时首先应根据变形参数来选择经济有效的抗震结构体系，可以说，这也是位移控制抗震设计方法的概念设计。自从上世纪九十年代以来，随着基于结构性能抗震设计理念逐步被地震工程界所认同，结构的位移控制抗震设计方法也越来越受到地震工程界的重视，对此展开了多方面的研究[1~3，5]。

2.直接基于位移设计的抗震设计方法

考虑如图1所示的具有n个自由度的多自由度结构体系，假设此多自由度结构体系按照假定的侧移形状产生地震反应，将其转换为等效设计单自由度体系，并假定多自由度结构体系与等效设计单自由度结构体系的基底剪力相等[4]。假设多自由度结构体系中第1自由度的假定侧向位移为δi，质量为mi，作用的侧向水平力为Fi，根据假设多自由度结构体系和等效设计单自由度体系的基底剪力均为Vb，等效设计单自由度体系的等效刚度为Keff，为最大等效设计位移时的割线刚度，等效设计位移为δeff，等效质量为meff，对应于位移为δeff时的等效设计单自由度体系的等效周期为Teff。

图1 原型多自由度结构体系与等效单自由度体系

将多自由度体系各质点的侧移δi除以等效位移δeff，并用ci表示，即：

显然，多自由度体系各质点的加速度ai与等效单自由度体系的加速度aeff也有类似关系：

则多自由度体系质点i的水平地震作用可以表示为：

由假定有：

则等效质量meff可以表示为：

假设水平地震力在两种体系上所做的功相等，即：

由式（1）、（3）、（4）、（6）可得等效单自由度体系的等效位移为：

代入式（5），可得等效单自由度体系的等效质量为：

单自由度体系的等效阻尼比ζeq包括二个部分：结构本身的固有阻尼比ζ；结构塑性变形附加的阻尼比ζ1。结构塑性变形附加的阻尼比ζ1采用Sozen提出的公式，按下式计算[5]：

根据现行的钢筋混凝土《建筑抗震设计规范》（GB50011—2010）[6]，当建筑结构所在的场地类别、设防地震等级确定，可以转换得到与阻尼有关的设计位移反应谱。在一定的阻尼水平下，给定等效单自由度体系的等效阻尼比ξeff，根据计算得到的设计等效位移δeff，由设计位移反应谱可以确定等效单自由度体系的等效周期Teff，由下式可计算设计等效刚度Keff：

则等效单自由度体系的基底剪力为：

由假设条件可知，多自由度体系的基底剪力也为Vb，将基底剪力沿多自由度体系的高度进行分布，则结构第i层处的设计水平侧向力Fi可由下式计算：

式中，hi为多自由度结构体系第i层，的层高；Wi为结构第i层的竖向作用力。

根据结构的水平地震力分布，计算结构的地震作用效应以及其他荷载作用效应，经适当的组合和选择合理的构件截面内力设计值，确定构件截面以及进行截面配筋计算，采取必要的构造措施，保证构件的变形能力。

3.位移反应谱

基于位移的抗震设计是以具有各种阻尼比的位移反应谱为基础的。弹性位移反应谱可通过两种途径来建立：一种是根据具体地点的强震纪录，通过数值积分求出结构自振周期T与其最大位移反应Sd之间的关系，这种需求曲线是一种形状不规则的曲线，该法主要对现有结构的抗震性能进行评估；另一种方法是由地震危险性分析确定建筑结构所在场地的地震地面运动，统计大量地震反应计算结果得到的结构需求曲线，这是一种能综合评估结构地震反应特性的方法，受到广泛的使用，目前该法主要是建立在规范定义的加速度反应谱基础之上的。规范采用相对于重力加速度的单质点绝对加速度即Sa/g与体系自振周期T之间的关系作为设计用反应谱。并将Sa/g用α表示，称α为地震影响系数，即：

由于加速度谱的广泛使用，所以目前主要是根据现行的建筑结构抗震设计规范的加速度反应谱Sa(T),按下式换算为位移反应谱：

其中：T为结构的自振周期；Sde和Sae分别为单自由度弹性体系的谱位移和谱加速度。

根据规范的加速度反应谱，由式（14）可得：

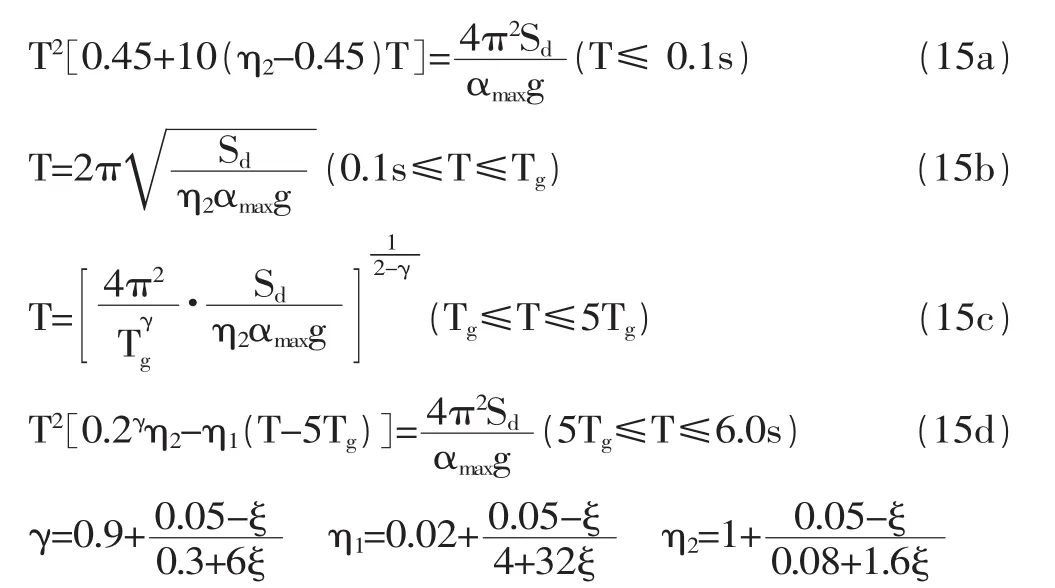
式中：αmax表示水平地震影响系数最大值。对于与基本烈度相应的多遇烈度地震和罕遇烈度地震,按现行规范取值；对于基本烈度地震,当设防烈度为7度、8度和9度时,分别取0.23，0.45和0.90。当已知等效单自由度体系的等效位移δeff（在式15中用Sd表示)、设防水准、所在场地的类别、阻尼比等参数,由式(15)可确定相应的等效周期Teff。

4.设计算例

式中：ξ=z/H为各层的高度比。

根据最底层的层间位移角1/800算出底层的侧移为5.25mm。由底层侧移和侧移形状系数得出顶层位移ut=22.45mm。在根据ut和每一层的侧移形状系数可算出各层的侧移δi。

根据每层的侧移δi和每层质量mi由式（7）计算所得等效位移δeff=17.16mm。然后由式（8）得等效质量Meff=3.254kN*s2/mm。

本工程为混凝土结构，本身的固有阻尼比ζ=0.05；结构的层间位移角为1/800，结构处在弹性状态，结构塑性变形附加的阻尼比ζ1=0。单自由度体系的等效阻尼比ζeq=0.05。

根据地震烈度7度小震（0.15g）αmax=0.12，Tg=0.45s，δeff=17.16mm，ζeq=0.05由式（15）计算出结构的等效周期Teff=1.16s。将Teff及Meff代入式（10）得等效刚度Keff=95kN/mm。按式（11）得基底剪力Vb=1630kN。计算结果见表1。

某工程为7层框架结构,各层层高1层为4.2m；2～7层为3.3m。设计基本地震加速度为0.15g，建筑场地类别为Ⅲ类，抗震设防烈度为7度，设计地震分组为第一组，场地特征周期值取0.45s。

对结构进行概念设计，1层的质量为6100kN；2～4层为5500kN；5～6层为5200kN；7层为4800kN。

本文假定在多遇地震作用下框架结构的性能水平为使用良好，取层间位移角为1/800。试验研究及理论分析均表明，对于质量和刚度沿高度分布比较均匀的框架结构，一般是底部一层或二至三层可能达到某一极限状态，即达到相应的层间位移角限值，而其他层的层间位移角均小于其限值。本文假定最底层最先达到极限状态。用作用倒三角形分布荷载的等截面剪切悬臂杆的侧移曲线作为框架结构的初始侧移模式[1]。框架结构的侧移形状系数按式（16）计算：

表1 基于位移的结构计算

按式（12）可得各楼层处的水平地震力作用。根据确定的各楼层处的水平地震力作用，计算结构的地震作用效应以及其他荷载作用效应，按照现行规范的设计方法进行荷载组合，进行结构构件设计。

5.结论

近年来国内外不少学者对建筑结构直接基于位移的抗震设计方法进行了大量的研究，本文简单介绍了该方法在实际工程中的应用。但是该方法还有很多问题需要进一步的解决[7]，如：（1）如何更加合理的确定结构的延性，如何合理的考虑等效阻尼比与延性的关系；（2）位移反应谱的建立，规范反应谱在转化为设计位移反应谱时还需要考虑哪些因素；或者如何根据大量的强震记录建立位移反应谱。

［1］梁兴文，黄雅捷，杨其伟.钢筋混凝土框架结构基于位移的抗震设计方法研究[J].土木工程学报,2005,38(9):53～60.

［2］M.S.Medhekar and D.J.L.Kennedy.Displacement-based Seismic Design of Buildings-Theory[J].Engineering Structures，2000，(22)：201～209.

［3］杨其伟，梁兴文，蒋建.钢筋混凝土框架——剪力墙结构基于位移的抗震设计方法[J].工业建筑,2007,37(2):1－5.

［4］钱镓茹，罗文斌.建筑结构基于位移的抗震设计[J].建筑结构,2001，31(4).

［5］Gulkan P.Sozen M.Inelastic response of reinforced concrete structures to earthquakes motions[J].ACI Journal，1974,(71):604－610.

［6］GB50011-2010.建筑抗震设计规范[S].北京：中国建筑工业出版社，2010.

［7］吉桉庆.直接基于位移的抗震设计方法研究[J].山西建筑,2009,35(30):69-71.