带缓冲簧的汽车减振器外特性及其敏感度分析

李仕生 徐中明 杨建国 张志飞

重庆大学机械传动国家重点实验室，重庆，400030

0 引言

减振器是汽车悬架的重要组成部分，其性能直接影响汽车的乘坐舒适性和操纵稳定性［1－2］。目前汽车中应用最为广泛的是传统悬架，而这种悬架的机械结构、刚度和阻尼都是不可调的，它只能保证在特定的工况下达到较好的效果。为了使传统减振器尽可能多地适应复杂多变的行驶工况，因此出现了在普通减振器的活塞杆上加装缓冲簧构成带缓冲簧的汽车减振器，如奥迪A6、帕萨特、富康、昌河北斗星、哈飞路宝等均使用了这种类型的减振器，由于该类减振器能有效地避免汽车在极差路面行驶时对其相应部位零部件的冲击与破坏，因此其应用越来越广泛。但对于带缓冲簧的双筒液压减振器，传统设计方法主要根据经验确定设计参数然后进行试验修正，需要进行反复调整，并经多次试制与试验，这种设计方法不仅周期长、成本高，而且较难获得最优的减振器特性［3］。基于此，从20世纪70年代开始，国外学者就开展了双筒液压减振器工作特性的建模分析研究。

目前，在双筒液压减振器的建模过程中，国内外学者均应 用 了 流 体 力 学 理 论［1－2，4－10］，且 大 多 对减振器的实际结构进行了较大简化，有的甚至只考虑了复原阀、压缩阀的工况，很少有学者深入分析诸如减振器活塞杆、内部气压、油液介质工作温度、摩擦力等对减振器阻尼力的影响规律。另外，对于底阀阀系采用纯阀片结构的减振器，其工作过程中阀片的受力变形属于“受均布载荷作用的环形薄板阀片挠曲变形”，但现有关于采用此方法建立减振器数学模型的文献却很少。同时，由于该减振器与普通减振器相比多了缓冲簧，缓冲簧起作用时的示功图的特点还未曾有报道。因此本文采用MATLAB软件，利用“受均布载荷作用的环形薄板阀片挠曲变形”方法建立数学模型，通过试验与仿真分析了带缓冲簧的汽车减振器外特性的特点，并就减振器活塞杆直径、内部气压、油液温度及摩擦力等因素对减振器外特性的影响及敏感程度进行了系统研究。

1 阀片弯曲变形微分方程

图1是减振器底阀阀系采用纯阀片结构时的装配示意图。阀片内圆是固定约束，其约束的内半径为ra，外圆是自由约束，外半径为rb，阀片厚度为δ，所受压力为p，在半径r处弯曲变形量为fr。

以节流阀片圆心为极点建立极坐标系，由于结构和载荷都是绕中心轴对称，根据弹性力学原理可得薄板弹性阀片弯曲变形曲面微分方程［11-13］：

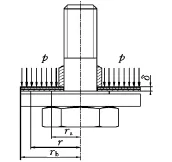
图1 阀片力学模型

式中，E为阀片弹性模量；μ为泊松比；r为半径，r∈ ［ra，rb］。

当多个阀片叠加时，δ需按等效厚度计算［13-14］，即

式中，δn为不同类型阀片的厚度；nn为不同类型阀片的数量。

因此，式（1）的通解可表示为

式中，f＊为方程的特解，f＊＝pr4／（64 D）；C1、C2、C3、C4为任意常数，决定于边界条件。

C1、C2、C3、C4的表达式为［12］

将C1～C4的值代入式（4）中即可计算出阀片在一定压力下任意半径r处的弯曲变形解析式fr。

2 油液流动机理分析

带缓冲簧的双筒液压减振器与普通双筒液压减振器一样，具有内外2个缸筒（工作缸和储油缸）、2个阀系（活塞阀系和底阀阀系）、4个阀（复原阀、流通阀、压缩阀及补偿阀），所不同的是在工作缸内的活塞杆上装有缓冲弹簧。油液在减振器内的流动有管嘴流动、环形薄板节流阀片所形成的薄壁小孔流动以及环形薄板阀片所形成的缝隙流动。

当管嘴流动时，其节流压差pg为［15］

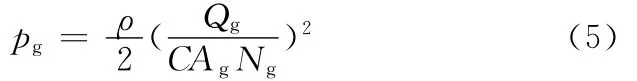
式中，ρ为油液密度；Qg为流经管嘴的油液流量；C为压力损失系数，取0.82；Ag为管嘴有效截面积；Ng为管嘴数量。

当环形薄板节流阀片缺口与阀体形成薄壁小孔流动时，其节流压差pz为［15］

式中，η为油液的动力黏度；Lz为阀体下端面凸起油线宽度；Qz为流经薄壁小孔的油液流量；bz为节流阀片缺口的总长度；hz为节流阀片缺口的高度。

当环形薄板阀片与阀体形成缝隙流动时，其节流压差pf为［15］

式中，Lf为缝隙的有效宽度；Qf为流经缝隙的油液流量；bf为环形薄板阀片与阀体下端凸起油线所形成的缝隙周长；ff为缝隙的开度。

当复原阀打开时，设复原阀阀片的开度为fh，则复原阀片的受力平衡方程为

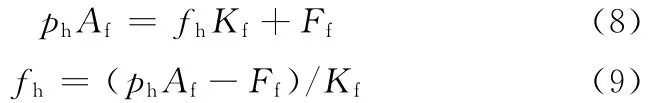
式中，Af为复原阀片受力面积；Kf为复原阀弹簧刚度；Ff为复原阀弹簧预紧力。

而复原阀打开时，油液在此处的流动属于缝隙流动，则由式（7）可得

式中，Lh为活塞阀体下端面凸起油线宽度；Qh为流经复原阀的油液流量；bh为活塞阀体下端凸起油线内圈周长。

联合式（8）～ 式（10），即可解出复原阀的节流压差ph。

当压缩阀打开时，油液在此处的流动属于缝隙流动，设压缩阀的开度为fy，则由式（7）可得其节流压差py的表达式：

式中，Ly为底阀座阀体下端面凸起油线宽度；Qy为流经压缩阀的油液流量；by为底阀座阀体下端凸起油线内圈周长。

根据压缩阀的结构参数，由式（4）可得到fy关于py的函数表达式：

联合式（11）、式（12），即可解出压缩阀的节流压差py。

油液流经流通阀或补偿阀时，阀片与阀体上凹槽两边凸起油线之间形成内外两条缝隙，由缝隙流动理论可得到流通阀或补偿阀处的节流压差pw为

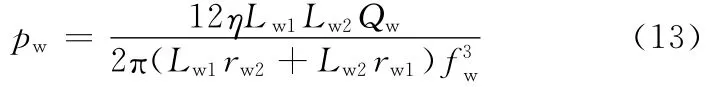
式中，Lw1、Lw2分别为阀体上凹槽两边凸起内外油线宽度；Qw为流经流通阀或补偿阀处缝隙的油液流量；rw1、rw2分别为阀体上凹槽的油线内外半径；fw为流通阀或补偿阀的开度。

若减振器的工作行程为±S，减振器工作过程中，缓冲簧的最大压缩量为A，缓冲簧的刚度为Kt，则缓冲簧的弹簧力Ft随活塞行程x变化的函数关系式为

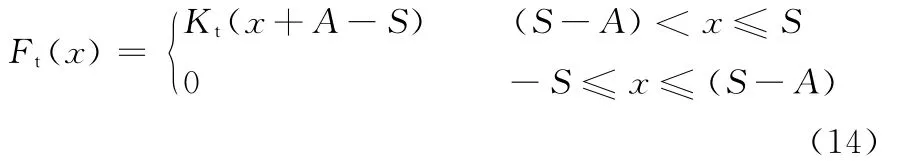
3 减振器油液流动动力学分析

图2为带缓冲簧的双筒液压减振器结构示意图，设储油腔内部气压为p0。

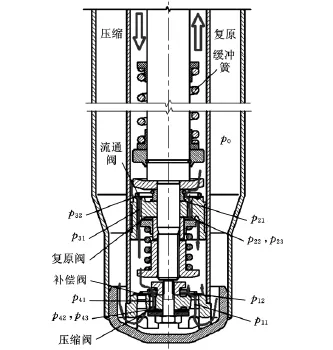
图2 复原及压缩行程中油液流动与压差的示意图

复原行程中，油液分两部分流动，一部分是油液由储油腔经底阀阀系流到下腔，另一部分是上腔油液经活塞阀系流到下腔。流经底阀阀系的油液，先流经底阀座补偿孔，设其节流压差为p11，再流经补偿阀阀片和底阀座上凹槽两边凸起油线之间形成的内外两条缝隙，其节流压差为p12。流经活塞阀系的油液先流经活塞复原孔，其节流压差为p21，再流经活塞下端的复原阀节流孔（复原阀开启前）或复原阀片与活塞下端面油线间的缝隙（复原阀开启后）流入下腔，其节流压差分别为p22、p23。

压缩行程中，油液也分两部分流动，一部分是油液由下腔经活塞阀系流到上腔，另一部分是下腔油液经底阀阀系流到储油腔。流经活塞阀系的油液，先流经活塞流通孔，其节流压差为p31，再经活塞上凹槽两边凸起油线和流通阀片之间的缝隙流入上腔，其节流压差为p32。流经底阀阀系的油液先流经底阀座压缩孔，其节流压差为p41，再流经底阀座下端的压缩阀节流孔（压缩阀开启前）或压缩阀阀片与底阀座阀体下端面油线间的缝隙（压缩阀开启后）流入储油腔，其节流压差分别为p42、p43。

3.1 复原行程

在复原行程中底阀阀系上下总压差为

将底阀座及补偿阀的相关结构参数分别代入式（5）和式（13）即可求出p11、p12，然后由式（15）即可求出p1。

在复原行程中，活塞阀系上下总压差为

将活塞及复原阀的相关结构参数分别代入式（5）～ 式（10）即可求出p21、p22、p23，然后由式（16）即可求出p2，其中，复原阀开启前p23＝0。

设活塞端面积为Ah，活塞杆横截面积为Ag，活塞及活塞杆在运动过程中的摩擦力为Fr，则复原阻尼力为

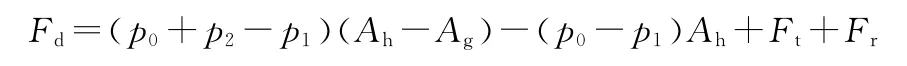
3.2 压缩行程

在压缩行程中活塞阀系上下两端的总压差为

将活塞及流通阀的相关结构参数代入式（5）和式（13）即可求出p31、p32，然后由式（17）即可求出p3。

在压缩行程中，底阀阀系上下总压差为

将底阀座及压缩阀的相关结构参数代入式（5）、式（6）、式（7）、式（11）和式（12），即可求出p41、p42、p43，然后由式（18）即可求出p4，其中，压缩阀开启前p43＝0。其压缩阻尼力为

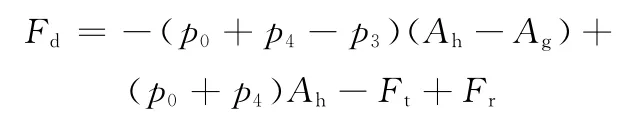
4 减振器外特性仿真与试验对比

根据减振器台架试验标准，在减振器台架测试设备上采用正弦激励方式对减振器进行测试。减振器阀系主要结构参数如表1所示。

表1 减振器阀系结构参数

4.1 不考虑缓冲簧时的示功图（力－位移曲线）

对减振器在缓冲簧不工作的行程范围内进行测试并仿真其示功图，测试行程为±25mm，得到0.05m／s、0.1m／s、0.3m／s、0.6m／s、0.8m／s、1.0m／s共6个速度点的示功图，如图3所示。减振器在各速度点的阻尼力如表2所示。

从图3可以看出：该减振器在各速度点的复原阻尼力和压缩阻尼力的示功图均饱满，无畸形；从表2中可看出，除0.05m／s时的压缩阻尼力误差较大外，其余各速度点的复原及压缩阻尼力仿真与试验结果符合性较好，误差均在15%以下。

4.2 速度特性曲线（力－速度曲线）

对减振器在缓冲簧不工作的行程范围内进行测试并仿真其速度特性曲线，速度范围为50～800mm／s，测试及仿真结果如图4所示。

从图4可以看出，减振器的阻尼力随活塞速度的增大而增大，模型仿真结果与试验结果趋势一致、符合较好。当活塞速度达到约150mm／s时，试验及仿真的复原阻尼力有明显的突变，此点就是复原阀的开阀速度点；当活塞速度达到200mm／s时，试验及仿真的压缩阻尼力有明显的突变，此点就是压缩阀的开阀速度点。试验数据证明了仿真对开阀瞬时速度的计算是比较准确的。

图3 试验与仿真的减振器示功图

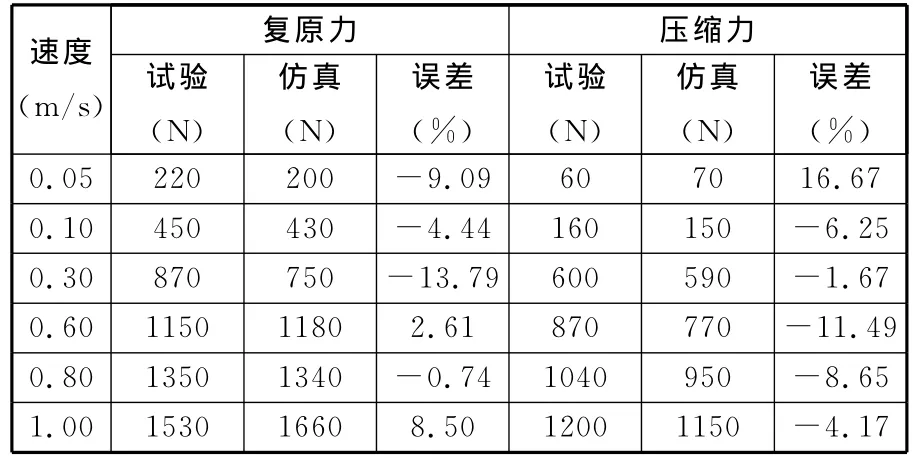
表2 减振器在各速度点的阻尼力

4.3 考虑缓冲簧时的示功图

将减振器测试的平衡位置上移，使其缓冲簧在减振器测试过程中的最大压缩量为15mm，在该工况下测试并仿真其示功图，测试行程仍为±25mm，得 到 0.05m／s、0.1m／s、0.3m／s、0.6 m／s、0.8m／s、1.0m／s共6个速度点的示功图，如图5所示。

比较图5与图3可以发现，当活塞位移在10～25mm范围内时，带缓冲簧时的复原阻尼力比无缓冲簧时的复原阻尼力大，带缓冲簧时的压缩阻尼力比无缓冲簧时的压缩阻尼力小。

从上述仿真和试验结果来看，该减振器的速度特性及不考虑缓冲簧与考虑缓冲簧时的示功图仿真结果都与其试验结果较好符合，误差较小。证明应用“受均布载荷作用的环形薄板阀片挠曲变形”理论及流体力学缝隙流动、管嘴流动及薄壁小孔节流理论建立的数学模型正确可靠。

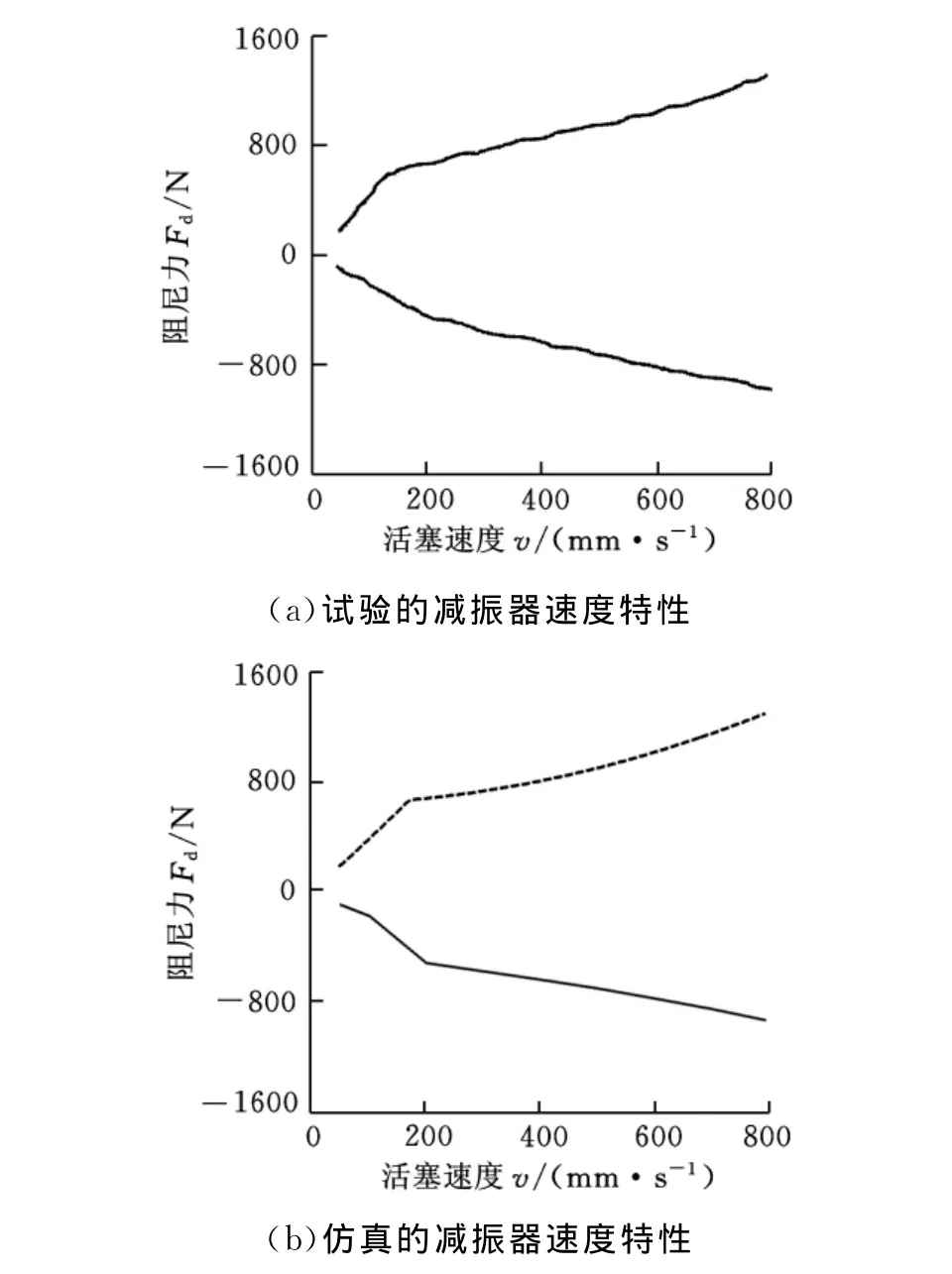
图4 试验与仿真的减振器速度特性

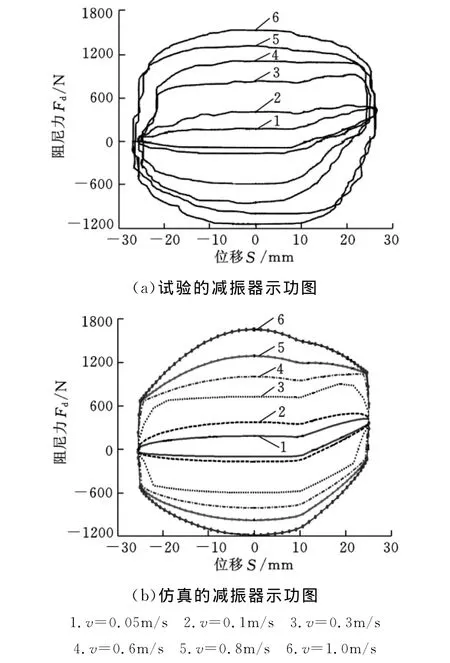
图5 试验与仿真的减振器示功图

5 减振器各参数敏感性分析

为了更好、更方便地将此模型应用于工程设计，并达到在设计过程中预测减振器外特性的目的，本文运用上述所建立的减振器模型对减振器活塞杆直径、内部气压、油液温度，以及摩擦力对其阻尼特性的影响及敏感程度进行了研究。其仿真结果如图6～图9所示。

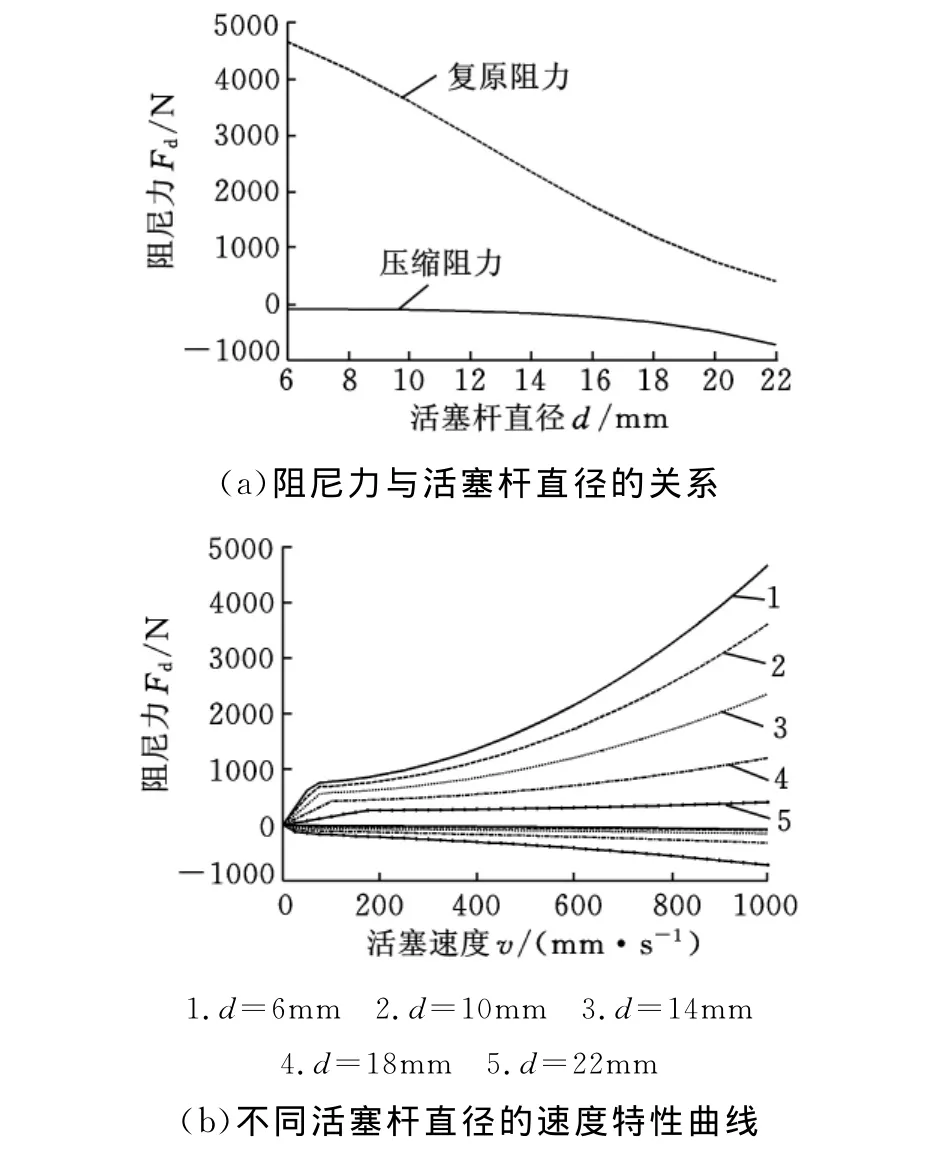
图6 活塞杆直径对减振器特性的影响

图7 减振器内气压对减振器特性的影响

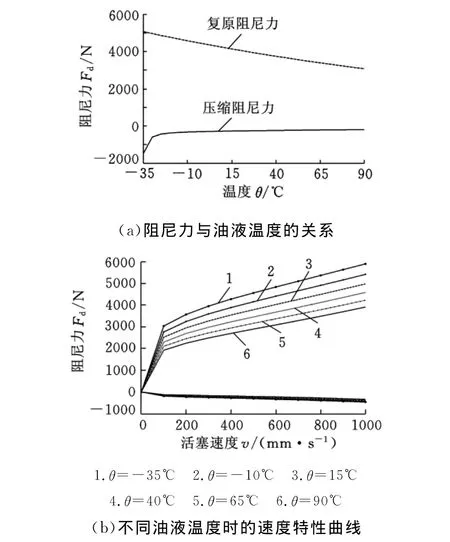
图8 减振油液温度对减振器特性的影响

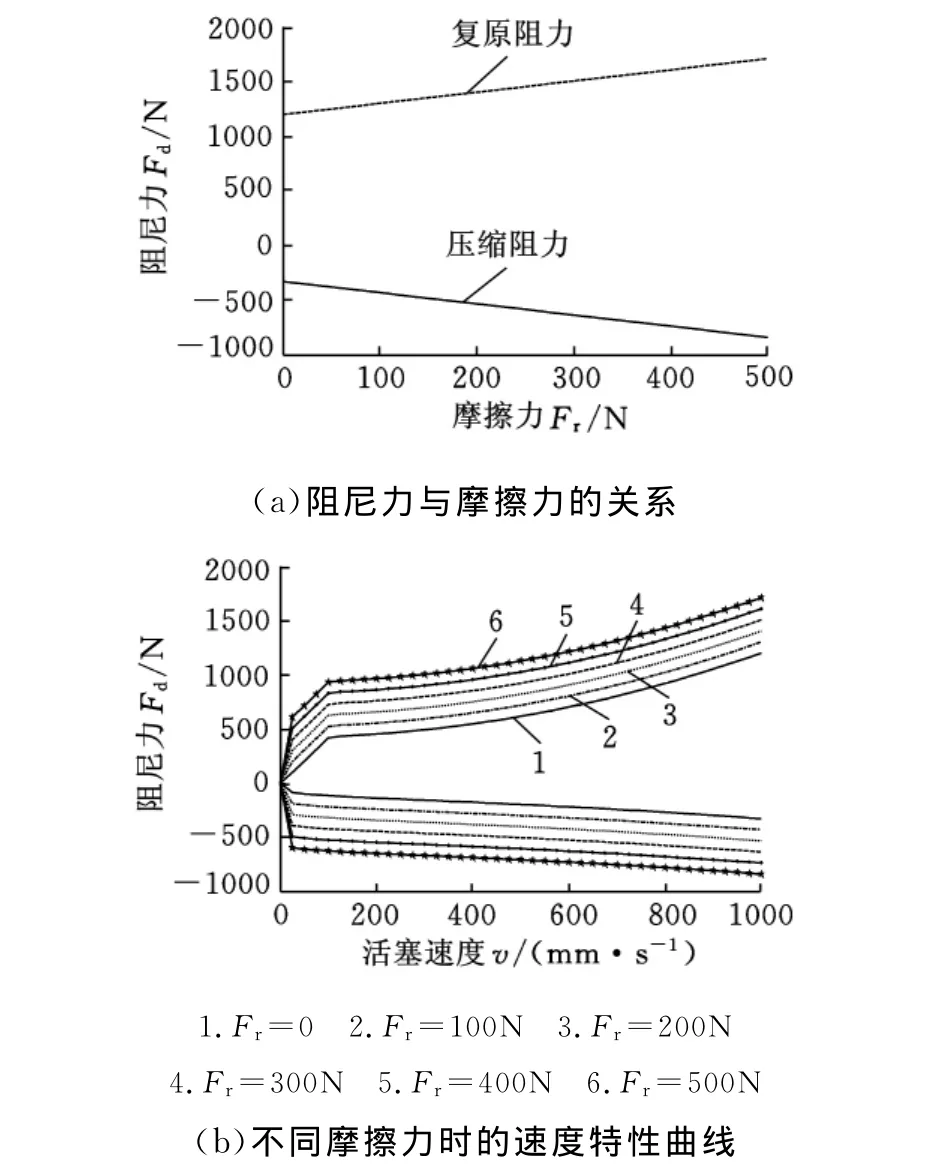
图9 摩擦力对减振器特性的影响

通过仿真阀系以外的各参数对减振器阻尼力的影响，可得到如下结论：

（1）由图6a可知，随着活塞杆直径的增大，减振器的复原阻尼力减小，压缩阻尼力增大；其敏感程度由图6b可知，活塞杆直径对减振器的低速段的阻尼力影响较小，而对高速段的阻尼力影响较大。

（2）当忽略减振器内体积变化对其内部气压的影响时，由图7a可知，减振器的复原阻尼力随着内部气压的增大而减小；压缩阻尼力随着内部气压的增大而增大；其敏感程度由图7b可知，气压对不同速度下的阻尼值基本上没有影响。

（3）由图8a可知，随着油液温度的升高，减振器的复原及压缩阻尼力都在减小，其敏感程度由图8b可知，油液温度对减振器低速段的阻尼力影响较小，对中速段的阻尼力影响较大，而对高速段的影响有限。

（4）由图9a可知，减振器的复原阻尼力和压缩阻尼力都随着摩擦力的增大而增大；其敏感程度由图9b可知，摩擦力对不同速度下的阻尼力基本上没有影响。

6 结束语

采用“受均布载荷作用的环形薄板阀片挠曲变形”方法，建立了带缓冲簧的汽车减振器的详细数学模型，模型中不仅应用了流体力学及弹性力学理论，还考虑了流通阀、补偿阀对减振器阻尼力的影响；对所建立的数学模型采用MATLAB软件进行仿真研究，将仿真结果和试验数据进行比较，其二者较好符合，证明应用上述理论建立的数学模型正确可靠；应用所建立的数学模型，分析了考虑缓冲簧时的减振器示功图的特点，同时还详细分析了活塞杆直径、内部气压、油液温度及摩擦力等因素对减振器阻尼力的影响规律及敏感程度，对这些复杂因素的考虑，使减振器阻尼特性的描述更为精确细致、更能准确地反映实际物理结构特性的规律，并为减振器的设计和性能预测提供了参考。

［1］Lee C T，Moon B Y.Simulation and Experimental Validation of Vehicle Dynamic Characteristics for Displacement Sensitive Shock Absorber Using Fluid－flow Modeling［J］.Mechanical Systems and Signal Processing，2006，20：373－388.

［2］Lee C T，Moon B Y.Study of the Simulation Model of a Displacement－sensitive Shock Absorber of a Vehicle by Considering the Fluid Force［J］.Journal of Automobile Engineering，2005，219（8）：965－975.

［3］任卫群，赵峰，张杰.汽车减振器阻尼特性的仿真分析［J］.系统仿真学报，2006，18（2）：957－960.

［4］陈龙，陈杨，江浩斌，等.节流口可调式减振器的性能分析与试验研究［J］.江苏大学学报.2004，25（3）：208－211.

［5］Zhou Changcheng，Zheng Zhiyun，Zhang Xueyi.Design Method for Throttle Holes Area of Telescopic Shock Absorber for Small Electric Vehicles［J］.Journal of Asian Electric Vehicles，2009，7（1）：1191－1197.

［6］郭孔辉，孙胜利.行程相关减振器的建模与试验［J］.吉林大学学报，2008，38（增刊）：32－36.

［7］Richard V K，Wang C C，Qian L X，et al.A New Shock Absorber Model for Use in Vehicle System Dynamics Studies［J］.Vehicle System Dynamics，2005，43（9）：613－631.

［8］Ramos J C，Rivas A，Biera J，et al.Development of a Thermal Model for Automotive Twin－tube Shock Absorbers［J］.Applied Thermal Engineering，2005，25：1836－1853.

［9］Calvo J A，Lopez－Boada B，Roman J L S，et al.Influence of a Shock Absorber Model on Vehicle Dynamic Simulation［J］.Journal of Automobile Engineering，2009，223（2）：189－202.

［10］李世民.筒式液阻减振器液－固耦合动力学特性仿真技术研究［D］.北京：清华大学，2004.

［11］周长城，顾亮，王丽.节流阀片弯曲变形与变形系数［J］.北京理工大学学报，2006，26（7）：581－584.

［12］陈轶杰，顾亮，管继富.减振装置节流阀片均布载荷变形解析计算［J］.重庆大学学报，2008，31（9）：988－991.

［13］周长城，顾亮.筒式减振器叠加节流阀片开度与特性试验［J］.机械工程学报，2007，43（6）：210－215.

［14］周长城，赵力航，顾亮.减振器叠加阀片的研究［J］.北京理工大学学报，2006，26（8）：681－684.

［15］Dixon J C.The Shock Absorber Handbook［M］.Great Britain：John Wiley ＆Sons，2007.