行波电渗流微泵的数值模拟和微泵流量影响参数研究

陈 波 晁 侃 吴健康

华中科技大学，武汉，430074

0 引言

电渗流是微机电系统中最重要的流体驱动技术之一。利用电渗流机理形成的电渗流泵具有易于加工和控制、无需移动部件、较高的可重复性和可靠性等优点。1998年，Ramos等［1］在实验研究过程中发现了交流电渗流现象，提出了交流电渗流的概念。利用交流电渗流驱动技术的低电压和交变信号，可在实现溶液混合的同时，极大地抑制电解反应的发生［2－7］。可见，研究交流电渗流微泵具有重要的理论意义和应用价值［8－11］。传统的交流电渗流采用非对称电极进行流体驱动，在实际应用中存在流量偏小的问题。最近的研究表明，在微通道壁面一系列离散电极上施加等相位差的交变行波电场，也能产生定向电渗流量［12－16］，一般称之为行波电场电渗流。相对于传统的非对称电极，在不增大交变电场强度的条件下，行波电渗流微泵可以明显提高微泵的流量［17］，而且电极高度对行波电渗流流量有重要的影响［18］。由于求解完整理论解析解非常困难，在行波电渗流的研究中，一般采用了简化的数学模型，即忽略双电层的厚度影响，在电极的壁面上采用滑移速度边界条件，将电场和流场解耦后进行计算［15－18］。这种方法一般只在双电层厚度相对于微通道特征尺度（如深度或宽度）比值极小，以及行波驱动电压小于双电层特征电压（25mV）时才近似成立［18］。但采用该种方法进行研究时，需要求解耦合的Poisson－Nernst－Planck（PNP）方程，计算难度大，国内外鲜见相关报道。Pribyl等［19］和 Hrdlicka等［20］成功地将该方法应用于交流电渗流的研究，但他们在对行波电渗流进行研究时，只考察了行波波长对电渗流流量的影响，而没有考虑通道深度对流量的影响。此外，Hrdlicka等［20］在研究行波电渗流时，用行波波长作为衡量双电层厚度相对大小的尺度并不准确，如当行波波长相对于通道深度较大时，仍然采用行波波长作为衡量尺度明显和实际情况不符。本文采用通道深度作为衡量双电层厚度相对大小的尺度，详细分析了驱动电压大小、行波波长以及双电层厚度和通道深度对电渗流微泵流量的影响。研究结果为行波电渗流微泵的研制提供了理论分析基础和数值模拟手段。

1 行波电渗流微泵的计算模型

1.1 行波电渗流微泵的结构

行波电渗流微泵由绝缘的基底材料（硅或玻璃）构成电渗流微通道，微通道的截面宽度远大于通道深度（y方向），其行波电渗流可简化为长度和深度（x－y）的二维流动模型。通过微加工技术在微通道内壁面粘贴一系列与电解质绝缘的离散微电极，每个电极施加振幅和频率相同，但存在相位差的交变电压，相邻电极的相位差角相等，形成行波电场。行波电渗流微泵的结构如图1所示。行波电场驱动通道内的溶液流动时，壁面电位允许近似采用连续的行波电场表示，即

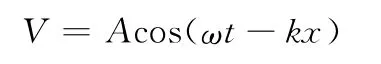
式中，A为行波电场幅值；ω为圆频率（物理频率为f＝ω／（2π））；k为波数，k＝2π／L；L为行波波长。

由于行波电场电渗流在微通道方向具有周期性，故只需截取一个行波波长L的微通道单元进行数值分析，各单元之间由重复的周期性边界条件连接。

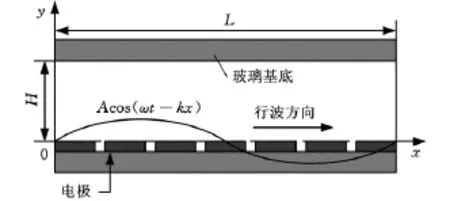
图1 行波电渗流微泵的结构

1.2 控制方程和边界条件

通道壁面采用无滑移边界条件，通道进出口采用周期性边界条件。微通道中充满电解质溶液，在行波信号的驱动下产生电渗流流动。不可压缩流体的连续方程和Navier－Stokes（NS）方程为

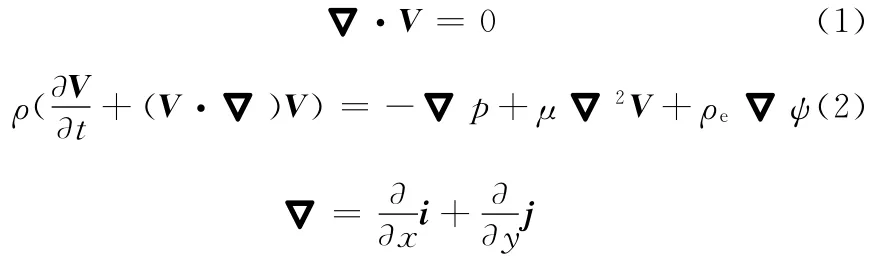
式中，i、j为x和y方向的单位矢量；ρe2ψ为作用于流体的行波电场力；V（u，v）为流体速度矢量；ρ为溶液密度；μ为流体黏度；p为压强；ρe为流体电荷体积密度；ψ为行波电场感应的电位势。

感应电位势ψ满足如下Poisson方程［21］：

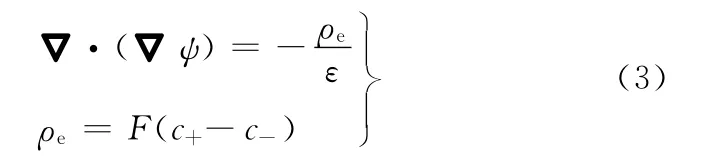
式中，c＋、c－为溶液正负离子摩尔浓度；ε为溶液介电常数；F为法拉第常数。

电极表面的行波电位势为

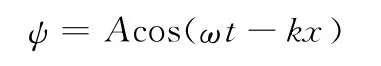
微通道上壁面为绝缘边界条件，n·2ψ＝0，其中，n为壁面法向矢量。

离子输运的Nernst－Planck方程为

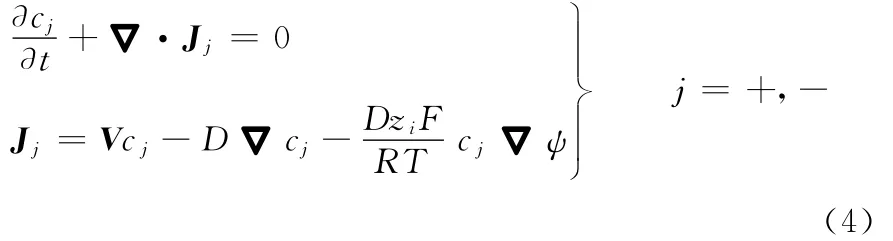
式中，D为离子扩散系数；R为摩尔气体常数；T为绝对温度。

忽略法拉第电流的影响，壁面边界条件为n·Jj＝0。

2 边界滑移近似

行波电压很小时，可忽略双电层的厚度影响，用简化的边界滑移模型求解行波电场电渗流［9-11］。由等效电路模型原理可知，若把双电层内被极化的流体区域当作电容，则双电层之外呈现电中性部分的流体则被视作电阻；电极表面采用电渗流Helmholtz－Smoluchowski速度为边界滑移速度，直接计算微通道内部电渗流。这等价于把双电层影响近似为壁面滑移速度，避开了双电层电场计算，其数值解得到大大简化。我们将上述的数值解称之为滑移边界近似解。对于图1所示的物理模型，电极上所施加的电位势在泵腔内的分布满足Laplace方程［11］：

若把电极表面双电层内的扩散层看成一个电容，则相应的电位势边界条件［11］为

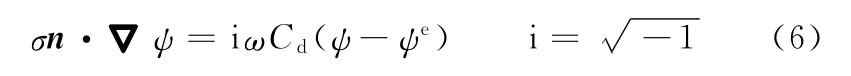
式中，Cd为双电层电容；σ为溶液电导率。

电极上的行波电位势为

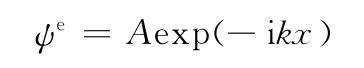
壁面绝缘层满足绝缘边界条件，通道进出口为周期性边界条件。

不可压缩Navier－Storks方程可简化为

微通道进出口为周期性条件，壁面绝缘层为无滑移速度边界条件。电极表面采用速度滑移边界条件：

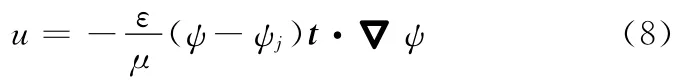
式中，t为电极表面切矢量。

3 计算结果分析

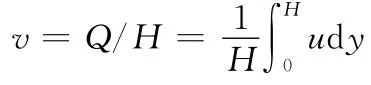
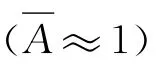
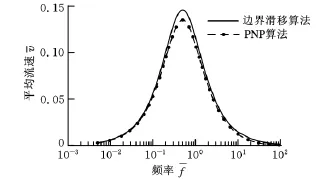
图2 泵流平均流速与行波频率关系≈1≈0.01）

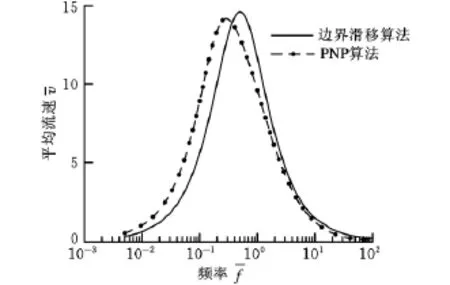
图3 泵流平均流速与行波频率关系≈10≈0.01）

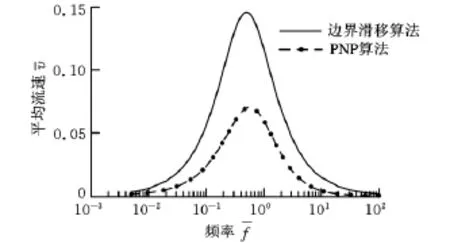
图4 泵流平均流速与行波频率关系≈1≈0.1）

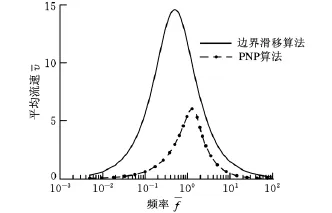
图5 泵流平均流速与行波频率关系≈10≈0.1）

将行波电渗流微泵的尺寸参数等比例缩小至原参数的1／10（H＝1μm＝λ／H＝0.1），平均流速与行波频率的关系如图4、图5所示。由于通道深度变小，边界滑移解往往会大于电渗流平均流速。在某些条件下，边界滑移解的平均流速甚至会大于行波波速［20］，表明边界滑移解明显有误。对较浅的微通道（较小的值），必须采用耦合PNP方程和NS方程求解。在壁面高电位≈10）、浅通道≈0.1）的情况下，边界滑移解误差会更大（图5）。

图6所示为泵流平均流速最大值与双电层厚度的关系，图6结果表明，由于忽略了双电层厚度的影响，边界滑移解的电渗流平均流速被高估。双电层厚度相对于通道深度比值越大，误差越明显。当双电层厚度比通道深度小很多时，边界滑移解与PNP解一致。

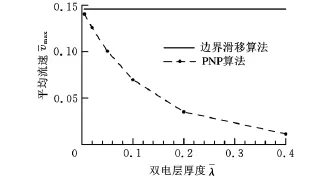
图6 泵流平均流速最大值与双电层厚度关系≈1）

为了研究行波波长对电渗流平均流速的影响，保持微泵深度不变（H＝10μm），波长深度比L／H 分别为2、4、6、10，电渗流平均流速与行波频率的关系如图7所示，图中≈0.01（相对深通道），溶液摩尔浓度c0＝10mol／dm3）。由图7可以看出，电渗流速度随波长增加而降低，速度峰值频率随着波长的增加而向低频转移。

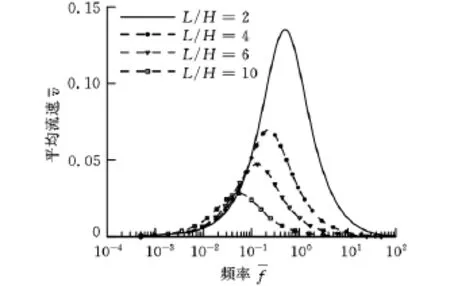
图7 泵流平均流速与行波频率关系≈1≈0.01）

在图8所示的泵流平均流速与行波频率关系中，令溶液摩尔浓度c0＝0.1mol／dm3，由Debye长度的定义可知≈0.1（相对浅微通道，λ ＝1μm）。由图8可以看出，电渗流速度随着波长的增加而降低，速度峰值频率亦随着波长的增加而向低频转移。

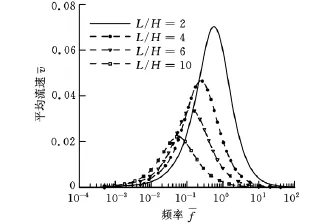
图8 泵流平均流速与行波频率关系≈1≈0.1）

4 结束语

采用滑移边界近似解，允许将电场和流场分开求解，虽可以简化数值解，但只能在双电层厚度相对于微通道深度和壁面极化电压都很小的条件下近似成立；对极化电压较高或双电层厚度相对于通道深度比值较大时，边界滑移解的实际电渗流速度会被高估。此前提下，耦合的PNP方程和NS方程是包含电渗流双电层的精确描述，能更加准确地对行波电渗流微泵进行研究。研究表明，当行波电场周期接近微通道双电层充电时间时，电渗流平均速度达到最大值。增大行波电场幅值，可以提高电渗流平均流速。当双电层厚度相对于通道深度比值和行波波长增大时，电渗流平均流速减小。

［1］Ramos A，Morgan H，Green N G，et al.AC Electrokinetics：a Review of Forces in Microelectrode Structure［J］.Journal of Physics D：Applied Physics，1998，31：2338－2353.

［2］Yoon M S，Kim B J，Sung H J.Pumping and Mixing in a Microchannel Using AC Asymmetric Electrode Arrays［J］.International Journal of Heat and Fluid Flow，2008，29：269－280.

［3］Gonzalez A，Ramos A，Green N G，et al.Fluid Flow Induced By Nonuniform AC Electric Fields in Electrolytes on Microelectrodes.Ⅱ.a Linear Double－Layer Analysis［J］.Physical Review E，2000，61：4019－4028.

［4］Green N G，Ramos A，Gonzalez A，et al.Fluid Flow Induced By Non－Uniform AC Electric Fields in Electrolytes on Microelectrodes.Ⅰ.Experimental Measurements［J］.Physical Review E，2000，61：4011－4018.

［5］Green N G，Ramos A，Gonzalez A，et al.Fluid Flow Induced By Nonuniform AC Electric Fields in Electrolytes on Microelectrodes.Ⅲ.Observtion of Streamlines and Numerical Simulation［J］.Physical Review E，2002，66：026305.

［6］Ramos A，Morgan H，Green N G，et al.AC Electric Field Induced Fluid Flow in Microelectrodes［J］.Journal of Colloid and Interface Science，1999，217：420－422.

［7］Ramos A，Gonzalez A，Castellanos A，et al.Pumping of Liquids with AC Voltages Applied To Asymmetric Pairs of Microelectrodes［J］.Physical Review E，2003，67：056302.

［8］Brown A B D，Smith C G，Rennie A R.Pumping of Water with AC Electric Fields Applied to Asymmetric Pairs of Microelectrodes［J］.Physical Review E，2001，63：016305.

［9］姜洪源，闫宝森，杨胡坤，等.交流电渗驱动机理及流速计算［J］.中国机械工程，2007，18（14）：1672－1675.

［10］姜洪源，杨胡坤，王扬.交流电渗微泵流速影响因素的研究［J］.传感技术学报，2008，21（7）：1089－1092.

［11］陈波，晁 侃，吴健康.非对称电极交流电渗微泵流体驱动研究［J］.中国机械工程，2011，22（3）：253－256.

［12］Ramos A，Morgan H，Green N G，et al.Pumping of Liquids with Traveling－wave Electroosmosis［J］.Journal of Applied Physics，2005，97：084906.

［13］Ramos A，Gonzalez A，Garcia－Sanchez P，et al.A Linear Analysis of the Effect of Faradaic Currents on Traveling－ wave Electroosmosis［J］.Journal of Colloid and Interface Science，2007，309：323－331.

［14］Gonzalez A，Ramos A，Castellanos A.Pumping of Electrolytes Using Travelling－wave Electroosmosis：a Weakly Nonlinear Analysis［J］.Microfluid Nanofluid，2008，5：507－515.

［15］杨胡坤，姜洪源，尚栋，等.行波电渗微流体驱动仿真和实验研究［J］.微纳电子技术，2009，46（3）：166－169.

［16］姜洪源，杨胡坤，敖宏瑞，等.行波电渗微流体驱动理论模型与实验［J］.光学精密工程，2009，17（5）：1093－1098.

［17］Yang Hukun，Jiang Hongyuan，Ramos A，et al.AC Electrokinetic Pumping on Symmetric Electrode Arrays［J］.Microfluid Nanofluid，2009，7：767－772.

［18］Garcia－Sanchez P，Ramos A.The Effect of Electrode Height on the Performance of Travellingwave Electroosmotic Micropumps［J］.Microfluid Nanofluid，2008，5：307－312.

［19］Pribyl M，Adamiak K.Numerical Models for AC Electroosmotic Micropumps［J］.Ieee Transactions on Industry Applications，2010，46（6）：2179－2189.

［20］Hrdlicka J，Cervenka P，Pribyl M，et al.Mathematical Modeling of AC Electroosmosis in Microfluidic and Nanofluidic Chips Using Equilibrium and Non－equilibrium Approaches［J］.Journal of Applied Electrochemistry，2010，40：967－980.

［21］陈波，晁 侃，吴健康.调控双电层电渗流数值研究［J］.分析科学学报，2011，27（1）：11－15.