材料强化因素对切削过程中尺寸效应的影响

叶贵根 薛世峰 仝兴华 戴兰宏

1.中国石油大学（华东），东营，257061 2.中国科学院力学研究所非线性力学国家重点实验室，北京，100190 3.山东大学威海分校，威海，264209

0 引言

切削过程中的“尺寸效应”被人们所熟知已经有相当长的时间，它是指切削比能随着切削厚度的减小反而呈现出非线性增加的趋势。尤其当切削厚度减小到微米量级时，“尺寸效应”表现得尤为突出［1］。切削比能是指切除单位体积工件材料所需的能量，表征了工件材料的抗切削能力，是描述切削过程最为重要的参数之一。因此在过去几十年里，围绕“尺寸效应”这一特殊现象国内外学者开展了深入的研究，试图对其进行解释和预测。目前关于“尺寸效应”的形成因素大致可归结为4类：①刀具圆角半径效应［2－3］；②工件次表面塑性变形效应［4］；③材料断裂分离效应［5－6］；④材料强化效应。在材料强化效应方面，Shaw［7］和Backer等［8］引入材料非均匀性来解释“尺寸效应”，认为随着切削厚度的减小，工件材料弱平面或缺陷存在的概率越小，材料强度就越接近理论强度，从而造成切削比能增大。Kopalinsky等［9］和 Oxley［10］则分别认为，切削厚度的减小将造成次剪切区温度下降和主剪切区应变率上升，从而导致材料相对强化，使得切削比能增大。Liu等［11］的研究进一步发现除了次剪切区温度因素外，应变梯度导致的材料强化也是形成“尺寸效应”的重要因素。可见，小尺度切削条件下发生的工件材料强化是“尺寸效应”产生的重要因素之一。然而材料的强化效应与众多因素相关，目前关于各种强化因素对“尺寸效应”的贡献仍不清楚，对于它们如何影响“尺寸效应”也不甚了解，仍然有待进一步深入研究。

众所周知，对于大多数材料而言，其流动应力取决于材料的应变、应变率和温度效应。因此，本文基于实验验证的有限元模拟技术，针对航天航空常用材料TiAl6V4进行系统的正交切削模拟仿真，深入研究各种条件下切削比能随切削厚度的变化规律，重点分析材料应变、应变率强化和热软化因素对“尺寸效应”的影响，探索“尺寸效应”产生的原因。

1 切削实验

为验证数值模拟方法的可靠性，我们针对航天航空常用材料TiAl6V4进行了不同速度的切削实验，通过对比相同切削条件下模拟与实验所获得的切屑形貌来验证数值模拟方法的有效性。整个切削实验在MIKRON UCP710数控车床上进行，如图1所示，TiAl6V4化学成分如表1所示。为尽可能保证正交切削条件，试件外径选取为100mm，从而可以近似忽略切削表面曲率的影响。刀具选用高硬度的YT15硬质合金刀具，其前角为0°，后角为7°，刀具圆角半径远小于切削厚度。切削过程中不使用任何冷却液，每改变一次切削速度，则更换新的刀具，从而将刀具磨损对切削过程的影响降至最低。

图1 数控车床切削示意图

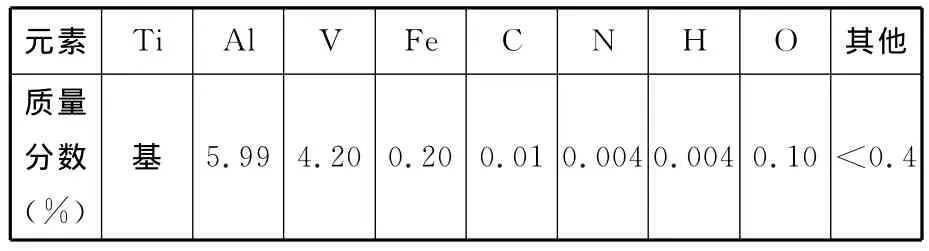
表1 TiAl6V4化学成分

实验过程中切削厚度固定为0.1mm，切削速度选取为3m／min、30m／min及90m／min。切削结束后收集各切削速度下获得的切屑，使用树脂镶样，经打磨抛光后使用n（HF）∶n（HNO3）∶n（H2O）＝1∶2∶50的体积比混合溶液腐蚀3～10s。通过对腐蚀后的切屑进行显微观测，发现随着切削速度的增加，切屑逐渐由连续变为锯齿状，并且锯齿状程度随着切削速度的进一步增加而愈加显著，如图2所示。在切削速度为3m／min时，切屑呈连续状，其宽度沿长度方向基本保持不变，切屑组织变形比较均匀，晶粒沿相同方向发生均匀的剪切变形［12］。当切削速度达到90m／min时，锯齿状形貌非常明显，并且在锯齿与锯齿间能发现明显的绝热剪切带［13］。

图2 不同切削速度下的切屑形貌

2 有限元模拟

2.1 切削模型及参数

本文采用大型通用有限元软件ABAQUS实现切削过程的二维模拟。工件和刀具的初始有限元网格划分如图3所示，工件网格划分采用双线性缩减积分、热－位移耦合以及平面应变四边形单元CPE4RT，并进行局部细化，刀具则设置为刚体并以恒定速度运动。切削参数与实验一致，刀具倾角为0°，后角为7°，切削距离为1mm，切削厚度为10～150μm。为了减小网格尺寸对模拟结果的影响，对于不同的切削厚度，切屑内的初始网格尺寸始终保持不变。同样，为消除刀具圆角半径对“尺寸效应”的影响，模拟过程中刀具圆角半径设置为0°。

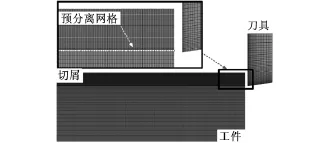
图3 切削有限元模型

2.2 切屑分离准则

本文采用在切屑和工件间加入预分离网格的方法实现切屑和工件的分离（图3）：预分离网格材料受到刀具挤压后发生变形，当其等效累积塑性应变达到临界值~εp时网格发生断裂失效，从而实现切屑和工件的分离。在本文中~εp设置为2，这样能保证预分离网格的断裂破坏速度，即切屑与工件的分离速度与刀具移动速度一致［14］。模拟过程中刀具以恒定速度运动，工件底端及远端固定。

2.3 刀－屑接触模型

根据Zorev［15］的研究，通常在切削过程中刀具和切屑发生摩擦的前刀面上有2个接触区域，即滑动区和黏着区。在滑动区，刀－屑摩擦服从库仑摩擦定律；在黏着区，刀－屑接触区的剪应力等于临界摩擦应力。整个刀－屑接触区域可描述为

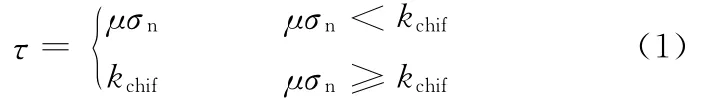
式中，τ为摩擦应力；σn为法向应力；kchif为材料剪切屈服应力，取其为455MPa；μ为刀－屑摩擦因数，取其为0.3［16］。

2.4 材料本构模型

由于实际过程中刀具变形非常小，因此在模拟中将其视为刚体，只考虑它的热传导效应。模拟过程中采用J－C本构模型来描述工件材料在高温、高变速率和大应变情况下的塑性流动行为，其表达式为

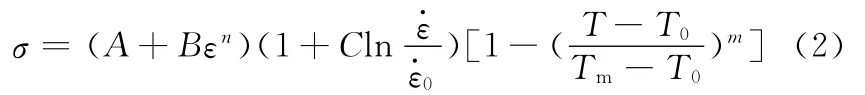
式中，σ为等效流动应力；ε、ε·分别为等效应变和应变率；A为准静态条件下的屈服强度；B、n为应变强化参数；C为应变率强化参数；m为热软化参数；ε·0为参考应变率；T、T0、Tm分别为工件温度、室温及工件熔化温度。

对于TiAl6V4而言，其流动应力与应变、应变率和温度都高度相关，各参数取值如表2所示［16］。

表2 TiAl6V4材料本构参数

3 模拟结果有效性验证

图4所示为切削厚度为0.1mm时，通过数值模拟所得到的不同切削速度下的切屑形态特征。通过切屑的等效塑性应变云图可以发现，随着切削速度的增加，切屑材料逐渐由均匀变形发展为局部剪切变形，导致切屑由连续状变为锯齿状，且锯齿状程度越往后越明显，这与实验结果一致。另外，通过图4我们可以发现，对于不同的切削速度，通过数值模拟所得到的切屑宽度、锯齿间距、锯齿最大及最小宽度与实际切削时的切屑形态能很好地吻合，这表明本文所采用的数值模拟方法是有效和可行的。

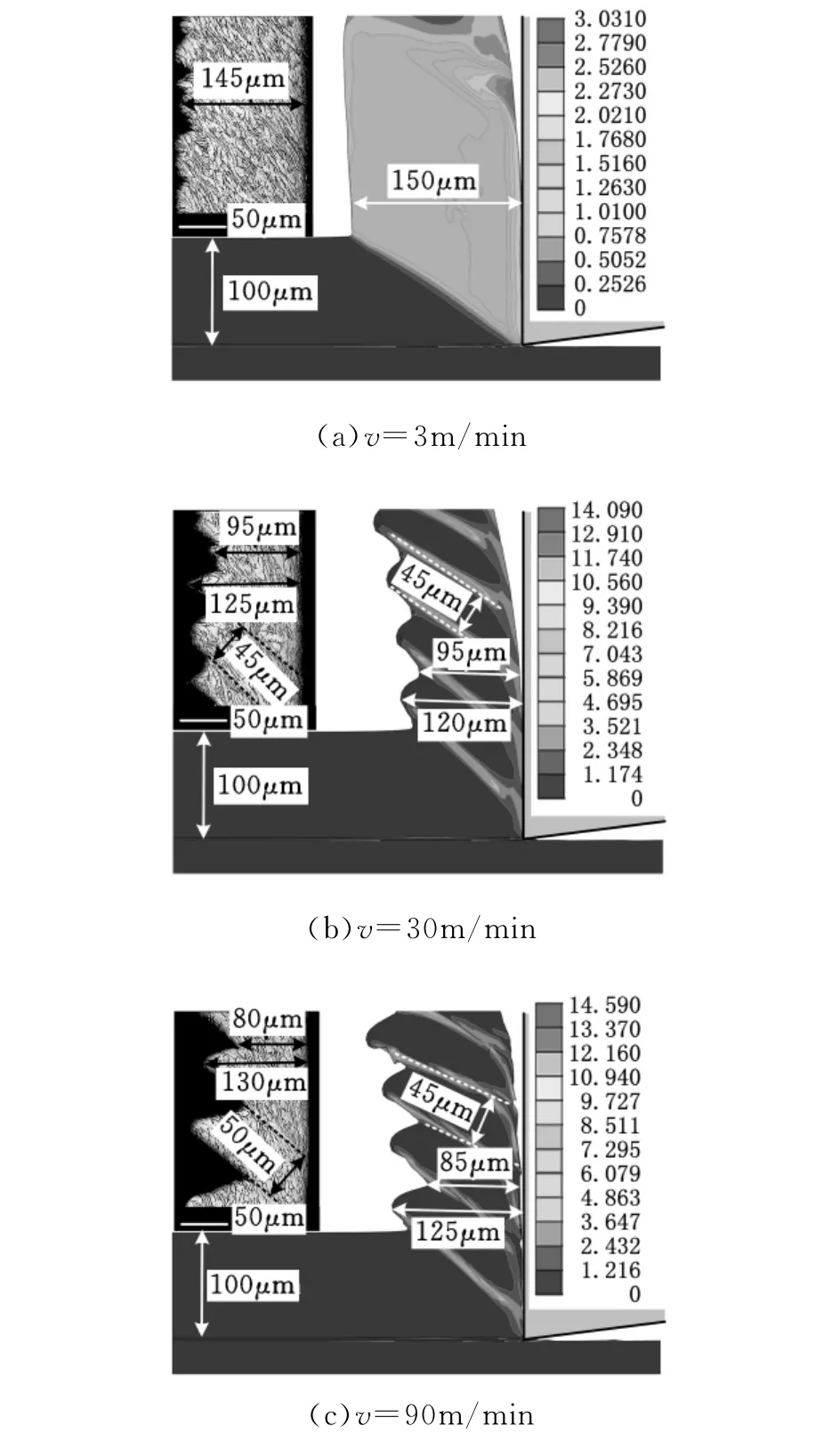
图4 数值模拟结果与实验结果对比（数值模拟结果显示的切屑等效塑性应变云图）

4 材料强化效应对“尺寸效应”的影响

为了研究材料应变、应变率及温度因素对“尺寸效应”的影响，我们在切削速度为60m／min、切削厚度为10～150μm范围进行了4组正交切削数值模拟仿真：第1组数值模拟综合考虑应变、应变率及温度对工件材料流动应力的影响，即材料本构关系遵循式（2）的流动变形行为，且各本构参数完全按照表2大小选取，材料的流动应力与应变、应变率和温度大小密切相关；第2组则只考虑应变率和温度对工件材料流动应力的影响，忽略应变强化效应，即在模拟过程中将应变强化系数B设置为无穷小（10－10）；第3组则只考虑应变和温度对工件材料流动应力的影响，忽略应变率强化效应，在模拟过程中将应变率强化系数C设置为无穷小（10－10）；第4组模拟则忽略热软化效应，只考虑应变和应变率对工件材料流动应力的影响，在模拟过程中将材料熔点和热软化指数设为极高值（Tm＝5000K，m＝1010）。

第一组模拟反映了真实的切削过程，其切削比能的模拟结果如图5所示。在综合考虑应变、应变率及温度对材料流动应力的影响时，切削比能表现出明显的“尺寸效应”现象，即随着切削厚度从10μm增加到150μm，切削比能由6250MPa降低到了2210MPa，并且切削厚度越小“尺寸效应”表现得越明显。其中切削比能由切削过程中的水平切削力除以切削宽度及切削厚度获得。

图5 切削比能随切削厚度变化曲线

4.1 应变及应变率强化因素对“尺寸效应”的影响

在切削过程中，除了刀－屑摩擦外，切削能量主要消耗于主剪切区和次剪切区材料的塑性变形上［17］，主剪切区和次剪切区材料的流动应力越大，切削过程中所消耗的能量也就越多。因此，如果某种强化因素使得主剪切区或次剪切区材料的流动应力随切削厚度的减小而增大，那么这种强化因素便很可能是“尺寸效应”形成的主要因素。为了探寻应变和应变率强化因素对“尺寸效应”的影响，我们针对第一组模拟结果，考察了主剪切区和次剪切变形区平均剪切应变和剪切应变率随切削厚度的变化情况，如图6和图7所示。由图6、图7所示可知，随着切削厚度的减小，主剪切区和次剪切区的平均剪切应变基本保持恒定，平均剪切应变率也没有像Oxley［10］所述的那样随着切削厚度的减小而上升，也就是说切削厚度的减小并没有使得主剪切区和次剪切区的工件材料由于应变或应变率提高而强化。由此可见，对于TiAl6V4材料而言，工件材料的应变和应变率强化因素并不是造成“尺寸效应”的主要因素。

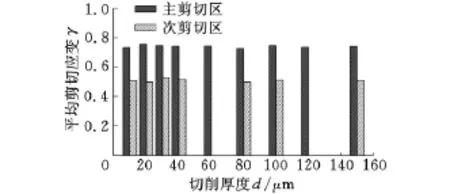
图6 主剪切区和次剪切区平均剪切应变随切削厚度变化规律

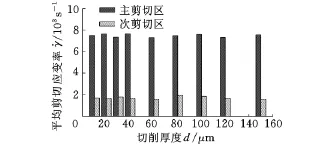
图7 主剪切区和次剪切区平均剪切应变率随切削厚度变化规律

为了进一步验证以上观点，我们对第2组和第3组模拟结果进行整理。通过第2组和第3组的数值模拟分析，我们可以分别得到在不考虑工件材料应变和应变率强化效应情况下的切削比能随切削厚度的变化规律，如图8所示。由图8可知，在不考虑工件材料的应变或应变率强化因素时，模拟结果同样能捕捉到明显的“尺寸效应”现象，并且切削比能随切削厚度的变化趋势与考虑应变或应变率强化因素时的变化趋势基本一致，这进一步表明，工件材料的应变和应变率强化效应对“尺寸效应”的产生没有太大的贡献。

4.2 热软化作用对“尺寸效应”的影响

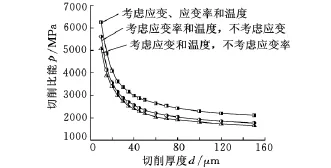
图8 应变和应变率强化作用对“尺寸效应”的影响

为了研究热软化作用对“尺寸效应”的影响，我们对第4组模拟结果进行了整理。基于第4组数值模拟结果，我们绘制了在不考虑材料热软化作用情况下的切削比能随切削厚度的变化曲线，如图9所示。在不考虑工件材料的热软化作用时，切削比能随着切削厚度的减小基本保持不变，从而无法捕捉到明显的“尺寸效应”现象。由此可见，“尺寸效应”现象随着材料热软化作用的消失而消失，这表明材料热软化作用是导致“尺寸效应”产生的重要因素。

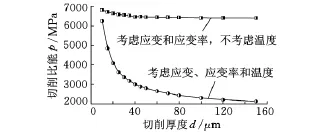
图9 热软化作用对“尺寸效应”的影响

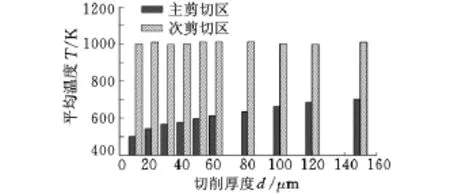
图10 主剪切区和次剪切区平均温度随切削厚度变化规律

为进一步分析“尺寸效应”形成的原因，我们基于第1组模拟结果，考察了主剪切区和次剪切区平均温度随切削厚度的变化规律，如图10所示。与Kopalinsky等［9］将“尺寸效应”归因于切削厚度减小造成次剪切区温度下降所不同的是，对于TiAl6V4而言，我们发现当切削厚度由10μm增加到150μm时，次剪切区温度基本保持不变，而主剪切区温度却上升达200K。如前文所述，切削过程中的能量主要消耗于工件材料的塑性变形及刀－屑间的摩擦耗能，其中塑性变形能又主要消耗于主剪切变形区。随着切削厚度的增加，主剪切区温度上升将导致工件材料软化，从而减小其塑性变形所需的能量，使得切削能整体降低，进而导致“尺寸效应”现象的产生。另一方面，虽然次剪切区的平均温度随切削厚度增大基本保持不变，但切削厚度的增加将导致刀－屑单位接触长度（刀－屑接触长度与切削厚度的比值）的减小，如图11深色柱状图所示。刀－屑单位接触长度的减小，一方面会缩短次剪切区长度，进而降低次剪切区内消耗的塑性变形能；另一方面还将减少刀－屑间的摩擦耗能，从而使切削比能进一步降低。此外，进一步的研究还表明，在忽略材料热软化作用时，刀－屑单位接触长度不再与切削厚度相关，如图11浅色柱状图所示。这表明随着切削厚度的增加，刀－屑单位接触长度非线性减小这一现象也是材料热软化作用所诱发的，原因可能是主剪切区材料高温软化后，导致切屑更容易发生卷曲变形从而更快脱离刀具的结果。由此可见，随着切削厚度的增加，材料热软化作用导致的主剪切区材料软化，以及刀－屑单位接触长度减小，是造成“尺寸效应”的主要原因。

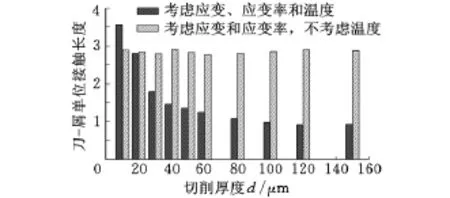
图11 刀－屑单位接触长度随切削厚度变化规律

4.3 高速切削条件下的应变、应变率及温度因素对“尺寸效应”的影响

由于上述结果都是在切削速度为60m／min的低速切削条件下获得的，而主／次剪切区材料的剪切应变、应变率和温度都会随着切削速度的增大而显著提高，从而有可能在高速切削条件下对“尺寸效应”产生影响。因此，有必要进一步研究600m／min高速切削条件下的材料应变、应变率强化及热软化因素对“尺寸效应”的贡献，如图12所示。研究结果表明，在600m／min高速切削条件下，切削力较60m／min有所降低，但切削比能仍然随着切削厚度的减小呈现出明显的非线性增强趋势。另外，由图12可知，在高速切削条件下，工件材料的应变和应变率强化因素对“尺寸效应”的产生仍然没有太大贡献，故材料热软化作用依然是导致“尺寸效应”产生的重要因素。

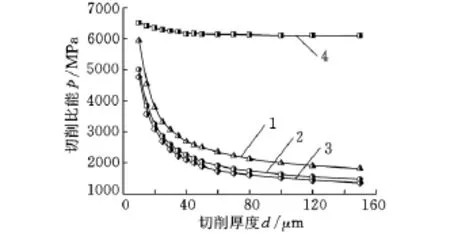
1.考虑应变、应变率和温度 2.考虑应变率和温度，不考虑应变 3.考虑应变和温度，不考虑应变率 4.考虑应变和应变率，不考虑温度

5 结论

（1）在高速和低速切削条件下都能捕捉到明显的“尺寸效应”现象。

（2）随着切削厚度的减小，主剪切及次剪切区的平均剪切应变和应变率保持恒定，材料应变和应变率强化因素对“尺寸效应”的形成基本没有贡献。

（3）材料热软化作用是导致“尺寸效应”产生的重要因素。随着切削厚度的减小，主剪切区平均温度非线性上升造成工件材料相对硬化，以及刀－屑单位接触长度非线性减小而造成的摩擦耗能增加，是导致“尺寸效应”形成的主要原因。

［1］陈勇平，唐进元.磨削加工中的尺寸效应机理研究［J］.中国机械工程，2007，18（17）：2033－2036.

［2］Schimmel R J，Endres W J，Stevenson R.Application of an Internally Consistent Material Model to Determine the Effect of Tool Edge Geometry in Orthogonal Machining［J］.Journal of Manufacturing Science and Engineering，2002，124：536－543.

［3］Komanduri R，Chandrasekaran N，Raff L M.Effect of Tool Geometry in Nanometric Cutting：a Molecular Dynamics Simulation Approach ［J］.Wear，1998，219：84－97.

［4］Nakayama K，Tamura K.Size Effect in Metalcutting Force［J］.Journal of Engineering for Industry，1968，90：119－126.

［5］Subbiah S，Melkot S N.The Constant Force Component Due to Material Separation and Its Contribution to the Size Effect in Specific Cutting Energy［J］.Journal of Manufacturing Science and Engineering，2006，128：811－815.

［6］Atkins A G.Modelling Metal Cutting Using Modern Ductile Fracture Mechanics Quantitative Explanations for Some Long Standing Problems［J］.International Journal of Mechanical Sciences，2003，45：373－396.

［7］Shaw M C.A Quantized Theory of Strain Hardening As Applied to the Cutting of Metals［J］.Journal of Applied Physics，1950，21：599－606.

［8］Backer W R，Marshall E R，Shaw M C.The Size Effect in Metal Cutting［J］.The Transaction of ASME，1952，74：61－74.

［9］Kopalinsky E M，Oxley P L B.Size Effects in Metal Removal Processes［J］.Institute of Physics Conference Series，1984，70：389－396.

［10］Oxley P L B.The Mechanics of Machining：an Analytical Approach to Assessing Machinability［M］.New York：Halsted Press，1989.

［11］Liu K，Melkote S N.Material Strengthening Mechanisms and Their Contribution to Size Effect in Micro－cutting［J］.Journal of Manufacturing Science and Engineering，2006，128：730－737.

［12］周泽华.金属切削原理［M］.上海：上海科学技术出版社，1993.

［13］王敏杰，段春争，刘洪波.正交切削切屑形成中绝热剪切行为的实验研究［J］.中国机械工程，2004，15（18）：1603－1606.

［14］Hortig C，Svendsen B.Simulation of Chip Formation During High－speed Cutting［J］.Journal of Materials Processing Technology，2007，186：66－76.

［15］Zorev N N，Wallace P W，Boothroy G.Toll Forces and Tool－chip Friction in Orthogonal Machining［J］.Journal of Mechanical Engineering Science，1964，6：422.

［16］Calamaz M，Coupard D，Girot F.A New Material Model for 2DNumerical Simulation of Serrated Chip Formation When Machining Titanium Alloy Ti－6Al－4V［J］.International Journal of Machine Tools and Manufacture，2008，48：275－288.

［17］Merchant M E.Mechanics of the Metal Cutting ProcessⅠ：Orthogonal Cutting and the Type 2 Chip［J］.Journal of Applied Physics，1945，16：267－275.