基于威布尔与模糊C均值的滚动轴承故障识别

王书涛 张金敏 张淑清 刘永富

燕山大学河北省测试计量技术及仪器重点实验室，秦皇岛，066004

0 引言

在滚动轴承运行过程中，提取振动信号时难免会受到大量非监测部件振动的干扰，造成有效信号的淹没，特别是滚动轴承的振动信号是经过复杂传递途经所得，并且故障信号非常微弱，往往造成故障信息淹没在背景噪声和干扰中，从而使信号特征提取及故障诊断变得异常困难［1－2］。

威布尔分布（Weibull distribution）是1939年瑞典人威布尔为描述材料疲劳强度而提出的一种统计模型，在产品疲劳寿命各可靠性分析中已获得极其广泛的应用。由于不同故障类型的威布尔分布模型的尺度参数、形态参数和威布尔负对数区别较大，能够较好地刻画轴承运行的状态特性，因而可以用作反应轴承运行状态的特征向量［3－5］。

聚类分析是多元统计分析的一种，也是非监督模式识别的一个重要分支。模糊C均值（fuzzy C－means，FCM）是一种基于模糊理论的聚类算法，将样本数据根据其相对于聚类中心的隶属度确定样本的亲疏程度而实现分类［6］。

本文提出一种基于威布尔分布的滚动轴承故障信息特征提取方法，以及模糊C均值的聚类方法，对故障进行识别。首先采用组合形态滤波器对原始信号进行消噪等预处理，对预处理后轴承信号建立威布尔分布模型，并提取威布尔分布的形态参数、尺度参数和威布尔负对数似然函数作为特征向量来表征轴承运行状态，然后采用模糊聚类对提取的特征向量进行模式分类和故障识别，并通过实验验证所提方法的有效性。

1 威布尔分布

1.1 威布尔模型建模

对于数据序列x，其具有双参数的威布尔分布函数为

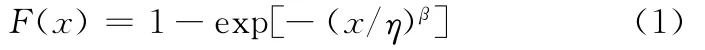
式中，β、η分别为形状参数和尺度参数，β＞0，η＞0；x为分布变量，x＞0。

该模型的分布密度函数为

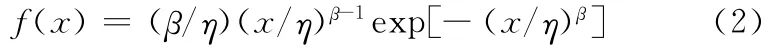
对于给定的一组由n个观察值组成的样本数x1，x2，…，xn（xi＞0），其建模步骤如下：

（1）重新安排数据，使其按增序排列，记这列有序数据为x′i（i＝1，2，…，n）。

（2）计算Xi和yi：

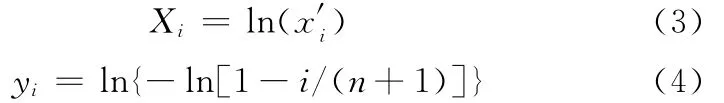
（3）在坐标纸上绘制（Xi，yi）的图形，从而得到原始数据的威布尔概率纸图（Weibull plotting paper，WPP）。如果数据图大体上沿一条直线分布，则该列数据可以用双参数威布尔模型建模。

1.2 威布尔分布模型的参数估计

用最大似然估计法对形状参数β和尺度参数η进行估计，设一时域振动信号的数据序列为x1，x2，…，xn，且符合威布尔分布模型，则其似然函数为

利用牛顿迭代法解式（7）可求得β的值，并将其代入式（8）即可求得η的值，从而可得威布尔分布负对数似然函数：

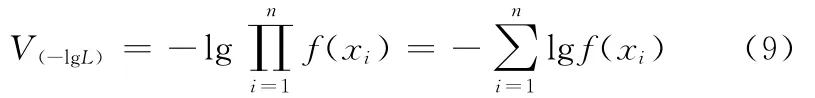
2 模糊C均值算法

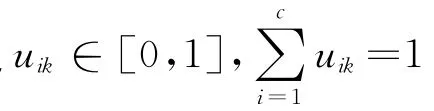
为了得到矩阵U，定义如下目标函数：

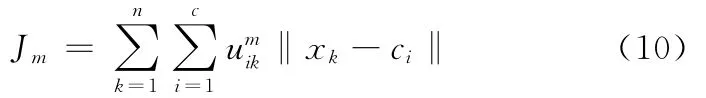
式中，m为模糊加权指数，要求m＞1，一般取为2；ci为c类中第i类的中心；‖·‖表示欧几里得距离。

为了找到目标函数的最小分区，采用迭代优化方法进行计算，其步骤如下：

（1）初始化分区矩阵U＝［uik］。

（2）计算所有c个类的中心：

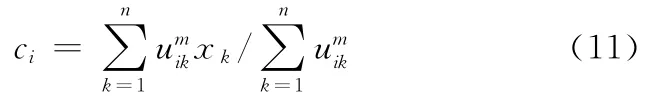
（3）更新分类矩阵U：

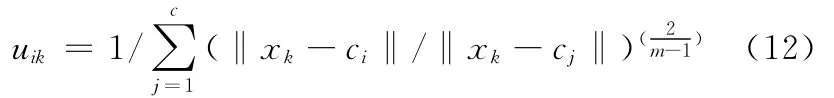
（4）对l＝1，2，…，给定判别的收敛精度ε＞0，直到 ‖U（l）－U（l－1）‖ ＜ε。

3 实验分析

图1 实验装置

实验数据来自美国华盛顿凯斯西储大学（Case Western Reserve University）电气工程实验室。实验装置如图1所示，主要由电动机、联轴器、扭矩传感器／译码器、功率测试器、电子控制器等部件组成。被检测的滚动轴承型号为SKF6205，轴承的故障包括外圈故障、内圈故障和滚动体故障，其中，轴承上所有类型的故障均为电火花加工的单点损伤，损伤点直径为0.1778mm。电动机通过与联轴器、扭矩传感器／译码器、测功机相连来驱动负载，运转转速通过扭矩传感器／译码器测得，其中电机所受负载可变。故障信号为用加速度传感器采集的故障轴承的振动加速度信号，加速度传感器放置在电动机风扇端或驱动端的轴承座上方，振动信号采样频率为12kHz。

3.1 基于威布尔分布模型的特征提取

当滚动轴承存在局部缺陷时，其振动信号中的脉冲信号含有丰富的缺陷信息。因此，首先对采集的滚动轴承原始振动信号用组合形态滤波［7－10］，消除振动信号中的背景噪声，同时保留原有的故障信息，然后对去噪后的振动信号建立威布尔分布模型，用极大似然法估计威布尔分布模型的尺度参数、形态参数和威布尔负对数，再提取这3个参数构建表征轴承运行状态的特征向量。故障特征提取步骤如下：

（1）建模。由威布尔分布模型可知，数据序列必须满足xi＞0，一般情况下获得的滚动轴承振动信号是在x＝0附近波动的，因而须对降噪后的信号进行处理，其表达式为

式中，x′i为降噪后的信号；δ为一经验值，一般取δ≤0.1‖min（x′i）‖。

对预处理后的信号建立威布尔分布模型，画出对应4种不同故障类型滚动轴承信号的威布尔概率纸图，如图2所示。

由图2可见，各图形大致呈一条直线，即样本数据基本服从威布尔分布模型。

如对式（13）选取不同δ值，可获得与图2中某一类型故障轴承信号相对应的威布尔概率纸图，图3所示为外圈故障轴承在δ分别取0.08、0.1时的威布尔概率纸图。

可见，无论δ取值如何，经式（13）处理后的数据均基本服从威布尔分布模型。

（2）估计参数。由所建威布尔分布模型，根据式（7）～式（9）估计出4种不同故障类型的威布尔分布模型的尺度参数、形态参数和威布尔负对数。

（3）构建特征向量。用估计出的尺度参数、形态参数和威布尔负对数构建特征向量Yi＝（βi，ηi，Li），其中i＝1，2，…，m，它表示第i个样本，m为样本总数。

不同故障类型的威布尔分布模型的尺度参数、形态参数和威布尔负对数区别较大，能够较好地刻画轴承运行的状态特性，因而可以用作反应轴承运行状态的特征向量。

3.2 基于模糊C均值的状态分类与模式识别

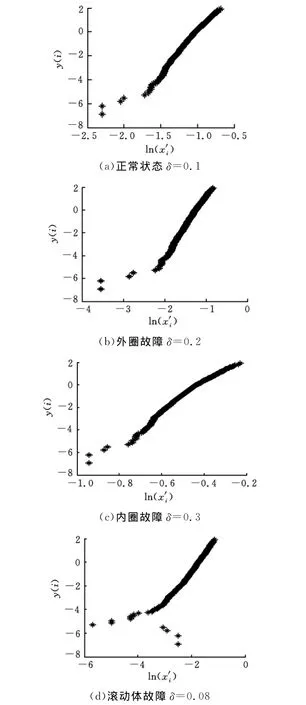
图2 各状态的WPP

4种状态下共有120个振动数据样本，各种状态下的数据子集分别包括30个样本。4种状态的轴承信号经形态滤波预处理后均服从威布尔分布，因此提取所有样本的威布尔模型的尺度参数、形态参数和威布尔分布负对数似然函数来描述轴承各种状态的信号特征，并组成120×3的故障特征矩阵。采用FCM聚类算法进行聚类，聚类组数c＝4，ε＝0.0001。对数据进行标准化处理［11］，经迭代计算并不断修正聚类中心，直至收敛为止。聚类结果如图4所示。

图4a为120组特征向量标准化后的FCM聚类空间分布图，图中，○为聚类中心。图4b为二维投影的聚类等高线图。从图4中可以看出，FCM聚类对形态滤波后信号的威布尔分布模型提取到的特征向量达到了故障诊断的效果。

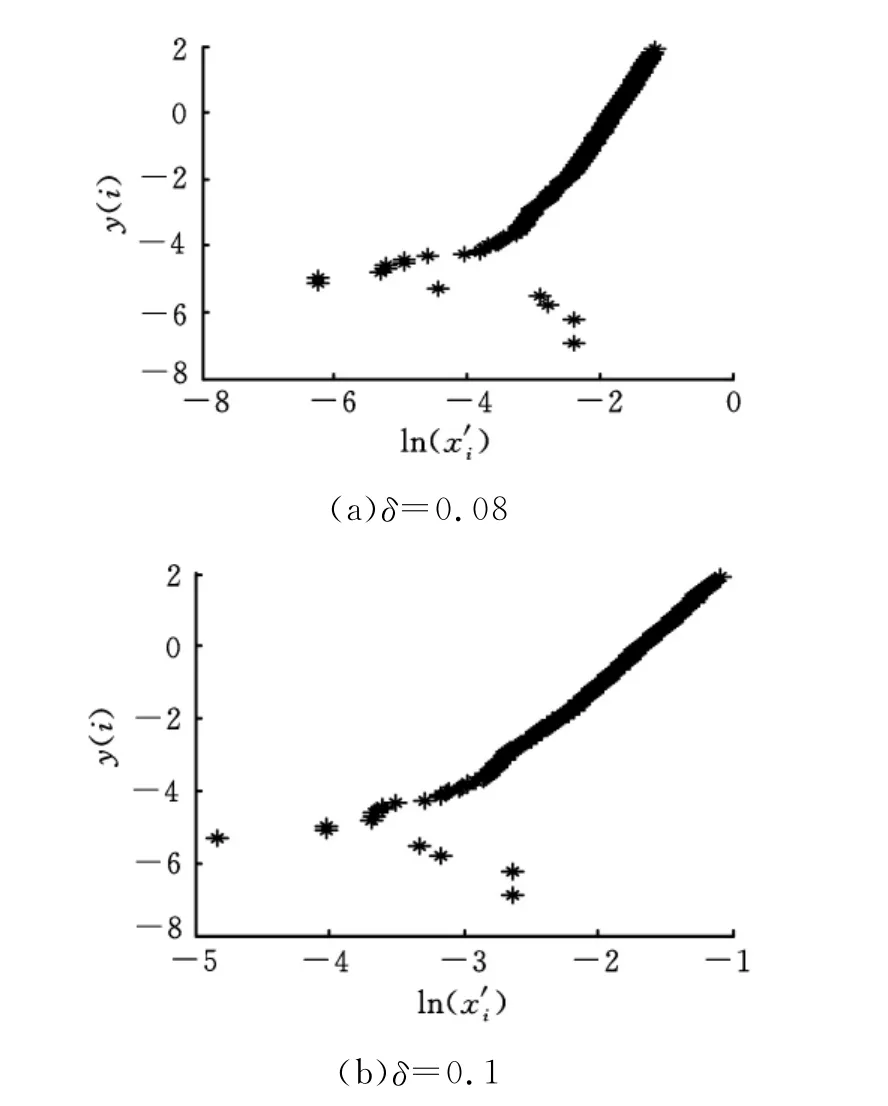
图3 不同δ值的外圈故障WPP

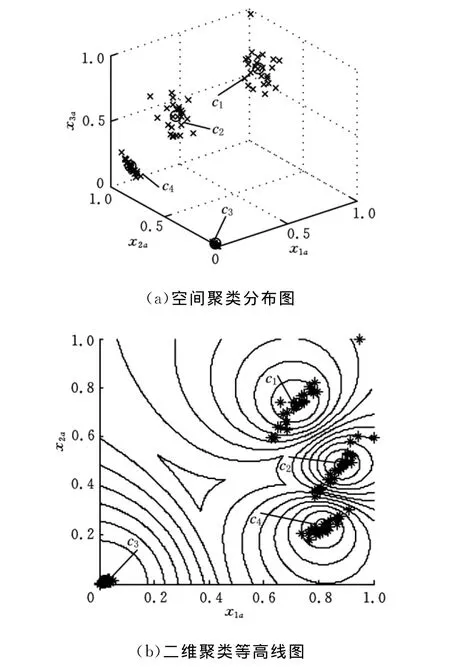
图4 空间聚类分布图和二维聚类等高线图

4 结论

（1）提出了一种基于威布尔分布与模糊C均值算法相结合的机械故障识别方法。滚动轴承振动信号经滤波去除噪声对故障信号的干扰后，进行威布尔分布建模分析，得出振动信号服从威布尔分布，进而提取威布尔分布模型的尺度参数、形态参数和威布尔负对数似然函数，作为振动信号的特征向量融入到FCM算法进行聚类分析，达到了故障诊断识别的目的。

（2）实验表明，威布尔分布与模糊C均值算法相结合运用到机械故障识别，准确率高，可以作为滚动轴承故障识别的重要手段，具有一定的实际应用价值。

［1］吕永卫，熊诗波，林选，等.基于小波包和EMD处理的滚动轴承故障诊断［J］.太原理工大学学报，2010，41（2）：178－182.

［2］胡爱军，唐贵基，安连锁.基于数学形态学的旋转机械振动信号降噪方法［J］.机械工程学报，2006，42（4）：127－130.

［3］Heng A，Zhang S，Tan A C C ，et al.Rotating Machinery Prognostics：State of the Art，Challenges and Opportunities［J］.Mechanical Systems and Signal Processing，2009，23（3）：724－739.

［4］Tai－Her Y，Li W.A Study on Generator Capacity for Wind Turbines under VariousTower Heights and Rated Wind Speeds Using Weibull Distribution［J］.IEEE Transaction on Energy Conversion，2008，23（2）：592－601.

［5］龙凯，李刚成.基于Hilbert变换与威布尔分布的轴承早期故障诊断［J］.科学技术与工程，2010，10（17）：4163－4166.

［6］康家银，纪志成，龚成龙.一种核模糊C均值聚类算法及其应用［J］.仪器仪表学报，2010，31（7）：1657－1663.

［7］郝如江，卢文秀，褚福磊.形态滤波器用于滚动轴承故障信号的特征提取［J］.中国机械工程，2009，20（2）：197－201.

［8］沈路，杨富春，周晓军，等.基于改进EMD与形态滤波的齿轮故障特征提取［J］.振动与冲击，2010，29（3）：154－157.

［9］Maragos P，Schafer R W.Morphological Filters Parth Their Set Theoretic Analysis and Relation to Linear Shift Invariant Filters［J］.IEEE Trans on ASSP，1987，35（8）：1153－1169.

［10］Maragos P，Schafer R W.Morphological Filters PartⅡ：Their Relation to Median，Order－statistic，and Stack Filters［J］.IEEE Trans.on ASSP，1987，35（8）：1170－1184.

［11］Lei Y G，He Z J，Zi Y Y，et al.New Clustering Algorithm Based Fault Diagnosis Using Compensation Distance Evaluation Technique［J］.Mechanical Systems and Signal Processing，2008，22：419－435.