离子双电层动态输运特性及电场对液体油膜压力的影响

马瑞珂 梅冰昂 左正兴

(北京理工大学机械与车辆学院 北京 100081)

随着润滑技术进入纳米级领域，薄膜润滑概念被提出。薄膜润滑的润滑膜膜厚范围在几十纳米之间，在这种极小间隙的摩擦中，双电层效应对润滑膜的影响不可忽略。在润滑过程中，摩擦副相对速度是变化的，所以需要对双电层润滑进行动态仿真。

在双电层机制的研究中，HELMHOLTZ[1]首先研究双电层现象，并提出平板双电层模型，该模型认为双电层类似于平板电容器，其正负离子分别在固液界面两侧整齐排列。但是在双电层中出现的动电效应该模型无法解释。于是GOUY[2]和CHAPMAN[3]提出了扩散双电层模型，对平板双电层模型进行改进。该模型认为溶液中的反离子以Boltsmann分布规律分布在液相中，靠近固液界面处离子浓度高，远离固液界面时浓度降低。扩散双电层模型能够解释双电层的动电效应，但是无法解释双电层中电势变号的问题。于是STERN[4]对扩散双电层模型进行改进，考虑离子尺寸有限，在固液界面处紧贴一层反离子与特性吸附离子，能较好地反映双电层的真实结构。Stern模型的双电层由紧密层和扩散层两部分组成，在固液滑移处与溶液本体之间的电势差被称为Zeta电势。GRAHAME[5]对Stern模型进行改进，将Stern层分为内Helmholtz面和外Helmholtz面，其中内Helmholtz面包含特性吸附离子，外Helmholtz面包含表面吸附反离子，为扩散层起始面。此后，许多学者对以Stern模型和Poisson-Boltzmann理论为基础的双电层模型进行改进[6-11]。双电层理论发展至今，主要应用于电化学储能领域[12]，在润滑领域应用尚不成熟。

针对润滑问题中的双电层研究中，BIKE和PRIEVE[13]在润滑分析中考虑了双电层的影响，在他们的模型中，外加电场使润滑区内形成双电层，双电层和润滑液流动产生的动电效应在固体上产生电动力，提高摩擦副承载能力，其结果表明，在其他条件相同时，更高的Zeta电势可以提供更高的承载能力。ZHANG和UMEHARA[14]在研究工程陶瓷摩擦中考虑双电层的影响，推导了考虑双电层效应影响的Reynolds方程，得到了表观黏度计算公式，并通过试验验证了其理论模型与试验数据基本吻合。黄平、王新杰等[15-16]对双电层对流体动力润滑和弹流润滑状态参数的影响进行了相关的理论分析。结果表明：在膜厚较薄(几十nm)时，双电层的存在对润滑膜的厚度有较明显的影响，可以使最小膜的厚度明显增加，随着膜厚的增加这种影响将迅速减弱；双电层的存在对润滑膜的压力影响不大，即使在膜厚很薄时，考虑和不考虑双电层得到的最大压力变化依然很小；双电层产生了电黏度现象，随着电场强度增加，电黏度现象加强，当电场强度超过某一值时电黏度现象减弱。白少先等[17-19]对双电层的电黏度效应进行研究，改进了ZHANG和UMEHARA[14]提出的表观黏度公式，提高了表观黏度计算值的可靠性与准确性。其研究结果表明，双电层对薄膜润滑的有效黏度和摩擦因数影响显著，使润滑膜黏度和摩擦因数明显增加。左启阳[20]对电解质的浓度与温度对双电层的影响进行了理论分析与数值分析，得出温度升高使双电层影响降低，而电解质浓度增加使双电层效应增强。

以上研究适用于稳态数值分析和试验验证，而未考虑瞬态变工况下的离子输运与润滑特性。针对该问题，本文作者提出双电层润滑动态多场耦合模型，考虑离子输运、流体流动与电场变化特性分析电压和摩擦副相对运动速度对负载变化的影响。

1 理论模型

1.1 仿真区域与模型假设

文中采用Poisson-Nernst-Plank模型(PNP模型)探究离子输运特性，采用Navier-Stokes方程探究流体运动特性。

图1所示为仿真区域，上下边界为壁面，左右两侧为润滑液入口与出口。上壁面固定，下壁面沿x方向移动，带动润滑液流动。摩擦副两壁面施加不同的电位使润滑区存在电场，两壁面形成双电层。为简化计算，模型有如下假设：(1)润滑液中含有2种离子，其离子价相反；(2)2种离子的扩散系数相同，离子有效直径相等；(3)润滑区内温度恒定，不考虑产热传热；(4)无滑移边界；(5)润滑液为不可压缩流体； (6)双电层只考虑扩散层，不考虑紧密层电势降低，故外加电势等于双电层滑移面电势(Zeta电势ζ)。

图1 双电层润滑模型Fig 1 Electric double layer lubrication model

1.2 控制方程

离子的连续性方程[21]为

(1)

式中:ci(i=1,2)为i组分量浓度；Ji为i组分离子质量传递摩尔通量，其公式[22]为

(2)

式中:u为流体微团速度矢量；Di为i组分扩散系数；zi为i组分离子的代数价；F为法拉第常数；R为理想气体常数；T为热力学温度；ψ为电势；NA为阿伏伽德罗常数；a为离子直径。

将式(2)代入式(1)得离子传质微分方程

(3)

电场中的泊松方程[23]为

(4)

式中：ε0为真空介电常数；εr为相对介电常数；ρe为空间电荷密度。

溶液中空间电荷密度为

(5)

将式(5)代入式(4)得润滑液中的泊松方程[24]

(6)

流场的动量方程[21]为

(7)

式中:ρ为溶液密度;p为压力;μ为动力黏度；f为体积力。

润滑区出口处流动电流[18]为

(8)

式中：h0为润滑区出口处膜厚；ux为流场速度x方向分量；r为润滑区宽度。

润滑区膜厚h为

h=ωx+h0+Bω

(9)

式中：ω为上壁面斜率。

润滑区电导L[18]为

(10)

式中：λ为润滑液电导率。

在流动达到稳定状态时，流动电流等于传导电流，即Is=Ic。假设流动电势引起的电场为匀强电场，且只考虑其x方向的分量，则根据欧姆定律，x方向流动电势引起的场强Ex为

(11)

在该模型中忽略重力，体积力只有电场力，流体微团的体积力为

(12)

式中：k为x方向单位向量;等式右边第一项为外加电势引起的电场力，第二项为流动电势引起的电场力。

将式(12)代入式(7)中得

(13)

流体流动的连续性方程为

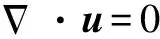
(14)

1.3 初始条件和边界条件

为求解控制方程组式(3)、式(6)、式(13)、式(14)，每个方程都需要设置初始条件与边界条件。

其中，初始速度u=0，初始压力p=0，初始离子量浓度c0,i=1 mol/m3，初始电势ψ0=0。

入口区(x=0)边界条件为

p=0

(15)

ce,i=1 mol/m3

(16)

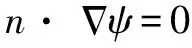
(17)

出口区(x=105nm)边界条件为

p=0

(18)

(19)

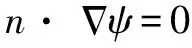
(20)

下壁面(y=0)处电势为ζ1，切向速度为v0，法向离子通量为0

n·Ji=0

(21)

上壁面(y=ωx+h0-Bω)处电势为ζ2,无切向速度，法向离子通量为0

n·Ji=0

(22)

1.4 参数取值

为数值求解上述控制方程组及其初始条件与边界条件，一共需要15个参数，包括离子扩散系数、温度、相对介电常数、溶液黏度、离子直径、润滑液电导率、阴离子与阳离子化学价、下壁面速度、上下壁面电势、入口处离子浓度、出口处膜厚、仿真区域长度、上壁面斜率。其取值或取值范围如表1所示。

表1 参数取值

1.5 仿真计算

文中使用COMSOL商用软件进行仿真，使用稀物质传递模块、层流模块和静电模块3个物理场接口耦合，得出仿真区域速度场、压力场、离子浓度场、电势场的分布。仿真区域主体采用自由三角形网格，网格最大允许尺寸为20 nm，仿真结果具有网格无关性。在靠近固-液界面处设置边界层网格，其初始尺寸为1.5 nm，网格增长率为1.02，可以精确反映固-液界面处物理量变化。

2 结果与讨论

2.1 PNP模型验证

图2所示为润滑区中段(x=5×104nm)电势沿y方向的分布曲线，其中上下壁面双电层Zeta电势差为0.1 V。可知，电势变化发生在2个双电层中，2个双电层之间的润滑液处于静电平衡状态。当下壁面速度接近0时(v0=0.1 m/s)，PNP模型与经典的PB模型结果一致。在v0=0.1 m/s时，双电层电势分布沿y方向对称分布，这是由于速度趋近于0时，2种离子出入口处摩尔流量大致相等，使润滑区内阴阳离子浓度相等，上下壁面双电层电荷密度分布一致，电势分布同Possion-Boltsmann模型的电势分布一致，由此可以验证模型的可靠性。而当壁面速度不为0时，上、下壁面电势分布不对称，并且当v0增大时，不对称程度增加。

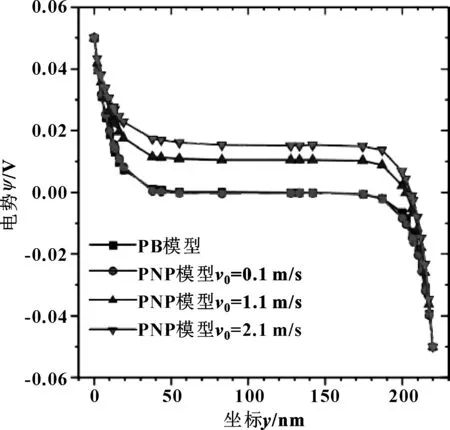
图2 不同模型的电势沿y方向分布(x=5×104 nm)Fig 2 Potential distribution along the y direction ofdifferent models(x=5×104 nm)

为阐明电势不对称性的原因，图3展示了入口处与出口处阴阳离子的流量随壁面速度变化的规律。可见，当上壁面固定、下壁面向右移动时，靠近下壁面的溶液流动速度远大于靠近上壁面的溶液流动速度。由于存在外加电势，上壁面双电层中大量聚集阳离子，下壁面双电层大量聚集阴离子，离子随溶液流动，垂直于流动方向的截面上阴离子流量始终大于阳离子流量。随着壁面速度增大，入口处2种离子流量大致相等，而在出口处阳离子摩尔流量小于阴离子摩尔流量，使阳离子在润滑区内积累，其润滑区内平均浓度大于阴离子平均浓度。

图3 离子出入口摩尔流量对比Fig 3 Comparison of ion molar flow at inlet and outlet(a)flow at inlet;(b) flow at outlet

进而，图4展示了不同壁面速度下阴阳离子浓度沿y方向的分布曲线。可知，当下壁面速度接近0(v0=0.1 m/s) 时，上下壁面双电层反离子量浓度大致相等，当下壁面速度较大(v0=1.1 m/s)时,上壁面阳离子量浓度(8 mol/m3)明显高于下壁面阴离子量浓度(3 mol/m3)。根据泊松方程(见式(4))，电势的梯度仅受电荷密度影响，而空间电荷密度由溶液中离子浓度和离子电荷量决定，文中模型中阴、阳离子电荷数相同，故而电势的梯度仅受离子浓度的影响。下壁面双电层中电荷密度为负值，电势的二阶导数为正值，电势沿y方向分布的函数为凹函数，负离子浓度增大时，该双电层电势的二阶导数增大，下凹程度增大，电势变化更快；上壁面双电层中电荷密度为正值，电势的二阶导数为负值，电势沿y方向分布的函数为凸函数，正离子浓度增大时，该双电层电势的二阶导数降低，上凸程度增大，电势变化更快。故得出双电层中反离子浓度越大，电势变化幅度越大。上述分析中，上壁面双电层反离子浓度大于下壁面双电层反离子浓度，所以上壁面双电层电势变化幅度大于下壁面电势变化幅度，液相平衡电势偏向下壁面Zeta电势，形成图2中所示y方向电势分布不对称现象。

图4 不同速度下阴阳离子沿y方向分布Fig 4 The distribution of anions and cations along the y directionat different speeds (a) x=5×104 nm,v0=0.1 m/s;(b) x=5×104 nm,v0=1.1 m/s

2.2 压力与承载能力

图5 不同Zeta电势下压力沿x方向分布Fig 5 Pressure distribution along the x directionunder different Zeta potentials

图6所示为不同壁面运动速度下最大承载能力随电势差的变化趋势。可知，承载能力随Zeta电势的增加而先增大后减小。这是由于双电层的动电效应引起表观黏度变化，在润滑区流体流动时，双电层反离子随流体运动，形成流动电流；反离子沿同一方向运动，沿流动方向积累，产生流动电势；流动电势阻碍反离子沿流体流动方向的运动，表现为阻碍了润滑区内流体的流动，降低了流速，表现为黏度提高，在摩擦副相对速度不变的情况下，承载能力得到提高，在假设润滑膜膜厚不变的情况下，最大压力也相对于无双电层时增加。而最大压力和承载能力降低的原因是双电层叠加引起电黏度降低[20]。

图6 不同壁面运动速度下双电层Zeta电势对承载能力的影响Fig 6 The influence of Zeta potential of electric double layeron bearing capacity at different wall speeds

为阐述双电层叠加现象，图7截取x=8.4×104nm处电势沿y方向分布。可知，电势差(ζ1-ζ2)增大使双电层厚度增加，电势差增大到0.3 V时电势变化趋于线性变化，双电层出现叠加现象;当电势差继续增大时，双电层叠加程度增大。双电层的存在可以使润滑膜表观黏度提高，但当双电层产生叠加时，由左启阳[20]的结论得双电层叠加使双电层电黏度效应降低。

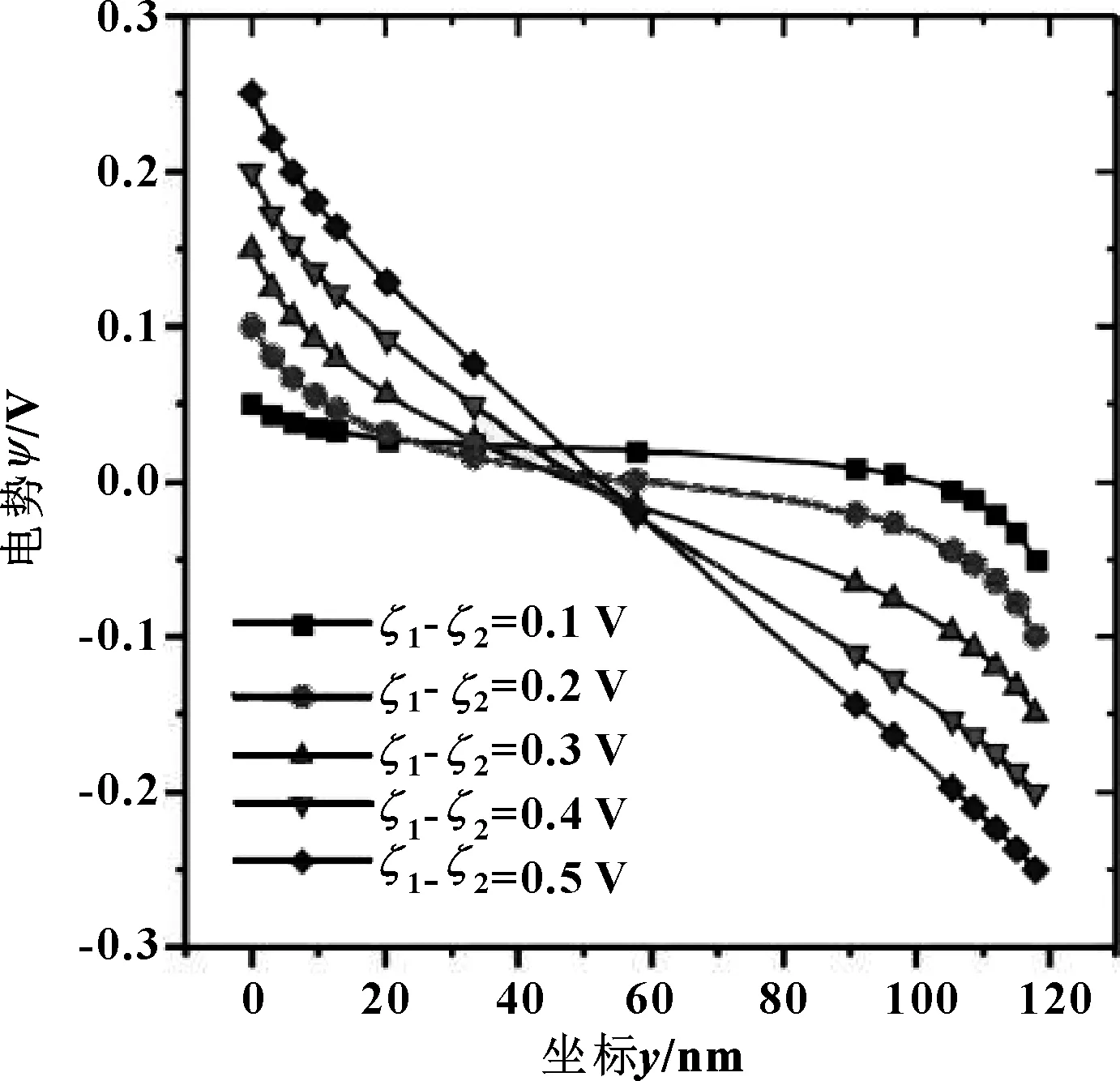
图7 不同Zeta电势下电势沿y方向分布Fig 7 The distribution of potential along y directionunder different Zeta potentials

3 结论

(1)为解决双电层动态仿真问题，综合考虑离子输运特性与流体流动及电场效应耦合作用机制，对双电层润滑进行动态仿真，通过将文中模型与经典Poisson-Boltsmann模型对比，分析电势分布与电荷密度分布，验证了模型结果的可靠性，为双电层润滑变工况的分析研究提供理论基础。

(2)探究摩擦副相对运动速度对润滑区域电势分布的影响，结果表明，摩擦副相对运动速度对双电层电势分布有显著影响，滑动壁的双电层电势变化比固定壁的双电层电势变化更大，随着相对速度增加，两个双电层电势变化程度的差距增大。

(3)探究双电层Zeta电势对双电层压力分布和承载能力大小的影响，结果表明，双电层影响润滑膜压力和承载能力，提高上下壁面电势差，压力和承载能力先增加后减少，这是由于双电层厚度增加使电黏度增加，但是双电层过厚产生叠加时电黏度又降低。