长径比对重载工况水润滑轴承性能的影响*

曹玉哲 梁 鹏，2，3 郭 峰 张晓寒 王 超 姜芙林

(1.青岛理工大学机械与汽车工程学院 山东青岛 266520；2.中国科学院兰州化学物理研究所,固体润滑国家重点实验室 甘肃兰州 730000；3.青岛理工大学工业流体节能与污染控制教育部重点实验室 山东青岛 266520)

水润滑轴承凭借其特有的节约资源、绿色无污染等特点，已广泛应用于船舶艉轴、水泵、水轮机等水下机械设备中，但由于水的低黏度特性，承载能力弱成为制约水润滑轴承发展的重要因素。

近年来，广大学者对弹流润滑状态下的水润滑轴承结构参数进行了一系列的研究。GAO等[1-2]利用有限元软件研究了不同结构尺寸的水润滑轴承承载能力，为轴承结构设计提供了参考。ZHANG等[3-4]通过理论计算分析了半径间隙、长径比等对水润滑轴承动态特性系数，以及轴径偏斜情况下水润滑轴承承载能力的影响，发现增大长径比可以减小轴承的刚度系数，提高轴承承载能力。邹争等人[5]通过正交试验评估了长径比、偏心率等对艉轴承变形程度的影响，发现长径比对变形量有显著影响。杨森[6]进一步研究发现，长径比对轴承弹性变形有较大影响，并且大长径比时轴承后端出现水膜不连续的状况，不利于轴承润滑。

然而，在重载或低速条件下水润滑轴承往往处于混合润滑状态[7]。因此，混合润滑状态下的水润滑轴承性能已成为研究热点。刘洋洋等[8]研究了低速条件下表面粗糙度对水润滑轴承混合润滑性能的影响，结果表明低速工况下水润滑轴承存在极大的粗糙峰接触压力。ZHANG等[9]采用分形理论描述表面粗糙形貌，发现分形维数对粗糙表面的摩擦学性能表征结果影响较大。XIE等[10-11]通过理论和实验分析了不同工况下水润滑轴承的润滑状态，研究了发生润滑状态转变时各参数的临界值。

综上所述，当前的研究多集中于轴承压力场的计算,而在重载工况的混合润滑条件下，两表面接触摩擦会产生较高热量使轴承温度升高，易导致轴承发生烧瓦、抱轴等故障，因此轴承温度场的计算不可忽略[12-13]。此外，长径比作为轴承结构的主要参数之一，对水润滑轴承润滑性能与冷却性能有着非常重要的影响。因此，本文作者通过建立水润滑轴承混合润滑热模型，研究长径比对重载工况下的水润滑轴承润滑性能和轴承温度的影响，为重载水润滑轴承的结构设计提供理论依据。

1 理论模型

径向水润滑轴承结构如图1所示，由于水的黏度低、轴承承载力小，在重载工况下水膜承载的同时常伴随表面微凸体接触承载，轴承处于混合润滑状态。图1中κ、ζ分别代表水平与竖直方向，Os、Ob分别为轴心和轴承中心，e、h为偏心距和膜厚，φ为偏位角，θ为圆周方向的角度，W、ω为载荷和主轴转速。

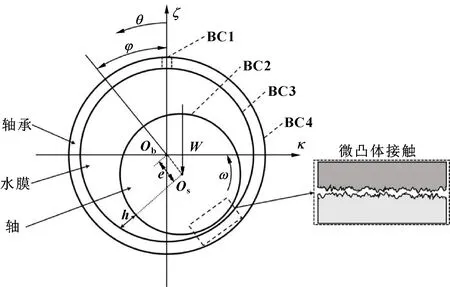
图1 水润滑轴承结构示意Fig 1 Schematic of water lubricated bearing

1.1 平均流量雷诺方程

基于平均流量模型[14-15]，并根据名义膜厚与平均膜厚之间的关系[16]，引入接触因子φc，得到平均流量雷诺方程：

(1)

式中:θ、y分别代表圆周、轴向方向;φθ、φy分别为θ、y方向的压力流量因子;φs为剪切流量因子;Rb为轴承半径;σ为轴和轴承两表面综合粗糙峰高度的标准差;h为名义膜厚(轴和轴承两表面粗糙度中线间的距离);p为水膜压力;η为水的黏度；us为主轴外表面的线速度。

1.2 微凸体接触模型

固体接触压力的计算采用Greenwood[17]微凸体接触模型：

(2)

(3)

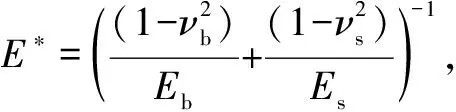
1.3 膜厚方程

由图1中几何关系，可推导出膜厚方程为

h=c+ecos(θ-φ)+δ

(4)

式中:c为半径间隙;e为偏心距;δ为轴承表面发生的弹性变形。

弹性变形计算采用Winkler假设[18]方法：

(5)

1.4 温度控制方程

根据能量守恒定律，流体的能量方程[19]为

(6)

式中：t为温度；cf、ρf、kf分别为水的比热容、密度和导热系数;u、v、w分别为水流在θ、y、z3个方向上的流速;Φ为热耗散做功。

假设轴承导热具有各向同性，则轴承热传导方程为

(7)

式中:zb代表轴承的厚度方向；kb为轴承导热系数。

1.5 边界条件

(1)压力场边界条件

压力场边界采用雷诺边界条件，具体形式为

(8)

式中：L为轴承宽度；θ0为水膜破裂位置的圆周角度。

(2)温度场边界条件

如图1所示，轴承采用顶部开槽供水方式，BC1～BC4分别代表进水口位置，主轴和水膜交界面，轴承和水膜交界面以及轴承外表面，各边界条件[20]分别设置为混合温度边界、热流通量为0边界、热连续边界以及对流换热边界，具体形式为

(9)

式中:Qsup、tsup分别为供水量(假设供水量等于端泄量)和供水温度;Qrec、trec分别为供水槽处的卷吸回水量和回流水平均温度；hb为轴承表面与空气的对流换热系数;t∞为环境温度；n表示操作面的外法线方向。

2 数值计算流程与模型验证

2.1 数值计算流程

对构建的混合润滑热模型采用有限差分法计算求解，计算过程如图2所示。与润滑油相比，水的物理性质较为稳定，所以计算过程中未考虑温度对水的黏度和密度的影响。

图2 计算流程Fig 2 Flow for the numerical calculation

2.2 模型验证

为验证润滑模型及计算程序的准确性，分别对文中构建的水润滑轴承混合润滑热模型的压力场和温度场进行了仿真结果验证，如图3所示。图3(a)展示了仿真结果与DOBRICA等[21]理论计算的压力场结果进行对比的曲线，图3(b)给出了仿真结果与FERRON等[22]实验测量的轴承温度场分布进行比较的曲线。结果表明，文中构建的水润滑轴承混合润滑热模型计算结果是准确可靠的。

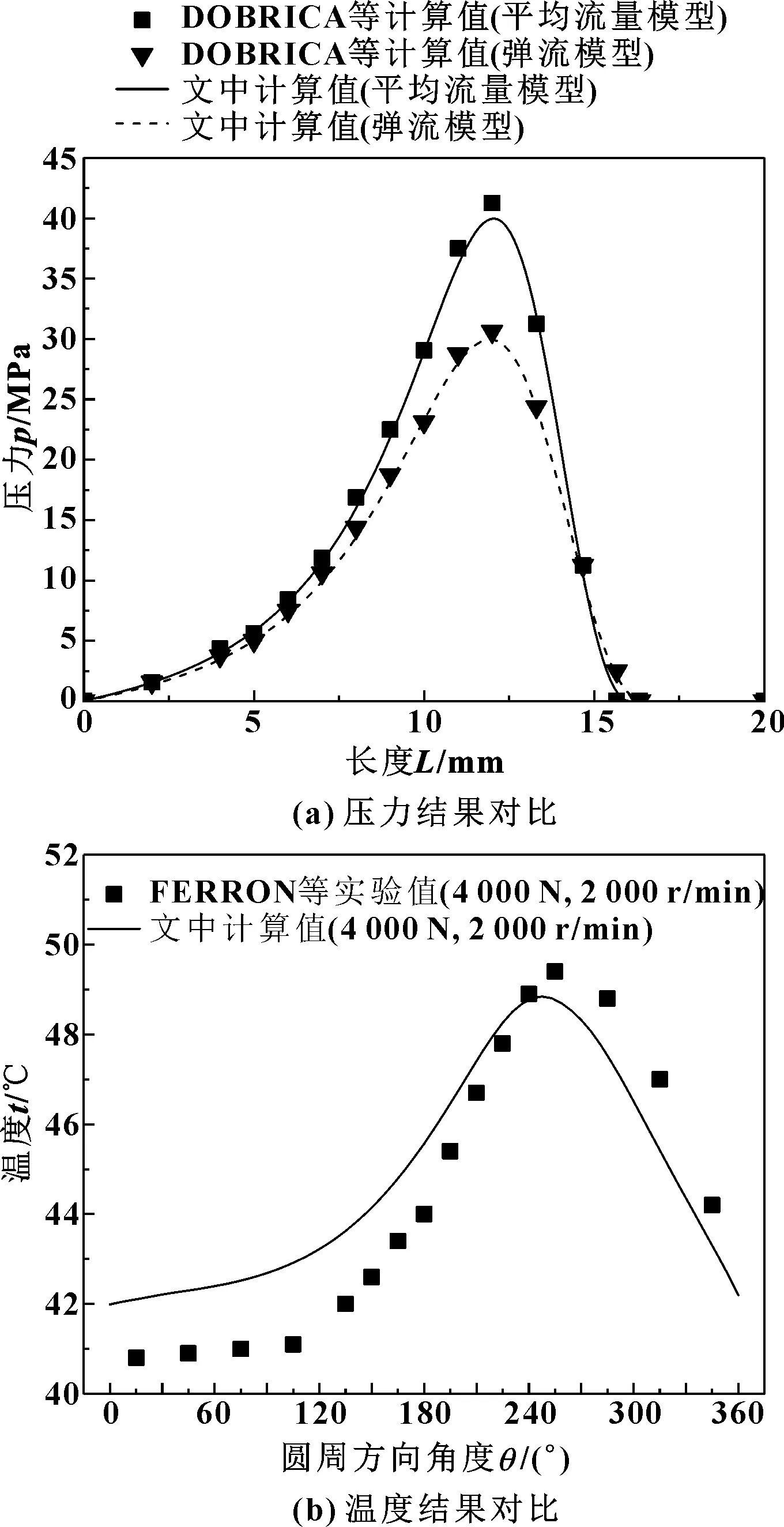
图3 模型计算结果验证Fig 3 Verification of calculation results of model (a)comparison of pressure results;(b)comparison of temperature results

3 结果与讨论

利用上述构建的润滑模型，理论计算了长径比分别为0.5、1.5、2.5时水润滑轴承在重载工况下的润滑性能，研究了长径比对重载水润滑轴承最小膜厚、压力、承载力、摩擦因数及轴承温度等主要参数的影响。所选轴承参数与工况参数如表1所示。

表1 轴承结构参数与工况参数

图4展示了载荷9 000 N时不同长径比的水润滑轴承最小膜厚及膜厚比随转速的变化曲线。可以看出，最小膜厚随转速及长径比的增大而增大，当转速较低时，在9 000 N的重载工况下最小膜厚低于10 μm，与粗糙峰高度在同一数量级。根据文献[10-11,17]，膜厚比(h/σ)小于4时，轴承处于混合润滑状态，而膜厚比小于1时，轴承处于边界润滑状态。因此，在图4中将膜厚比为1和4的水平线标出分别作为边界润滑与混合润滑、混合润滑与弹流润滑的分界线。可以看出，在长径比为0.5且转速低于1 210 r/min的工况下，轴承始终处于边界润滑状态，并且随着转速的进一步升高轴承进入混合润滑状态，但最终未能进入弹流润滑状态；而长径比为1.5与2.5的轴承在低速时工作在混合润滑状态，随转速的升高进入弹流润滑状态，其起飞转速(由混合润滑状态进入弹流润滑状态时的临界转速)ω1.5、ω2.5分别为2 460、1 340 r/min。上述分析表明增大长径比可提高最小膜厚、降低轴承进入弹流润滑状态的起飞转速，有利于改善轴承润滑状态。

图4 不同长径比下最小膜厚和膜厚比随转速的变化(9 000 N)Fig 4 Variation of minimum film thickness and film thicknessratio with rotating speed under different length-diameterratio at load of 9 000 N

图5所示为载荷9 000 N时长径比对水润滑轴承最大压力值及压力分布的影响。其中图5(a)给出了3种长径比的水润滑轴承最大水膜压力和最大固体接触压力的变化曲线。可以看出，3种长径比的最大水膜压力和最大固体接触压力的变化趋势基本相同。在低速重载工况下最大固体接触压力较大，此时轴承处于混合润滑或边界润滑状态；随着转速的升高，动压效应增强，水膜压力逐渐增大到峰值；但随着转速的进一步升高，逐渐增强的动压效应使得主轴偏心率减小，导致最大水膜压力慢慢减小。最大固体接触压力则随转速的增大一直减小，其减小速度随长径比的增大而加快，当长径比为1.5和2.5时主轴加速至起飞转速后最大固体接触压力减小为0。还可以发现，相同转速工况下，最大水膜压力与最大接触压力均随长径比的增大而减小。

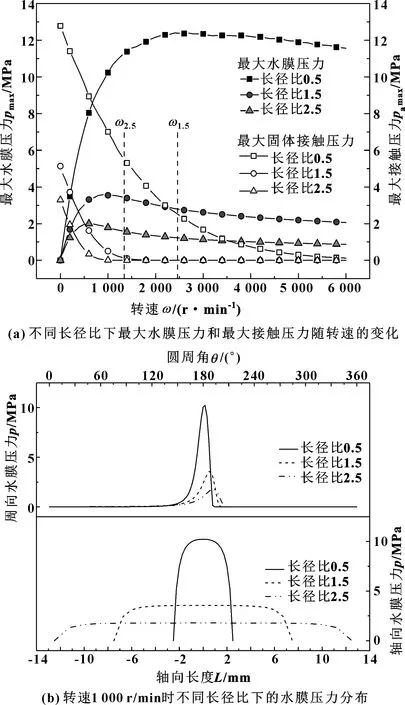
图5 长径比对最大压力和压力分布的影响(9 000 N)Fig 5 Effect of length-diameter ratio on maximum pressure andpressure distribution at load of 9 000 N(a)variation ofmaximum of hydrodynamic pressure and contact pressurewith rotating speed under different length-diameter ratio;(b)pressure distribution under different length-diameterratio at rotating speed of 1 000 r/min

为进一步研究长径比对水膜压力的影响，图5(b)给出了转速1 000 r/min时3种长径比的水润滑轴承水膜压力的周向和轴向分布。可以看出，长径比为0.5时，较小的承载区域内产生了一个高达10 MPa的压力峰，如果轴承长时间工作在此状态下，容易因应力集中导致轴承疲劳失效。而随着长径比的增大，水膜压力峰值迅速减小，并且在周向上压力峰值出现的位置稍向水膜发散区移动。当长径比增加至2.5时压力峰值减小至1.8 MPa(降幅达到82%)，显著降低了应力集中效果。并且随着长径比的增大，轴向水膜有效承载区域增加，水膜压力分布也更均匀。因此增大长径比可改善轴承压力分布，提高轴承寿命。

不同长径比时水润滑轴承水膜承载力和固体接触承载力随转速的变化曲线如图6所示。可以看出，低速重载工况下主要由固体接触承载，但水膜承载力随着转速升高而增大，并逐步成为主要承载部分，而固体接触承载力随转速升高而减小。当长径比为1.5和2.5时，固体接触承载力在主轴转速达到起飞转速后降为0；而长径比为0.5时的固体接触承载力虽接近于0但不完全为0，这是因为该长径比下轴承一直处于混合润滑状态(从图4中的膜厚比可以看出)。并且随着长径比的增大，水膜承载力的增大速度与接触承载力的减小速度得到加快，即长径比的增大会加快实现水膜承载的主体地位。

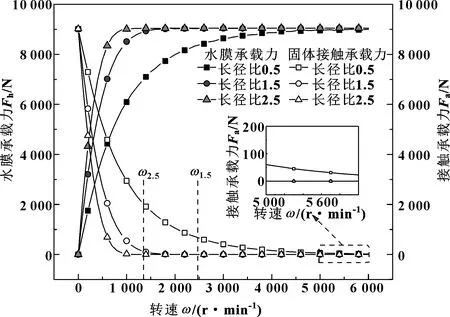
图6 不同长径比下轴承承载力随转速的变化Fig 6 Variation of capacity with rotating speed underdifferent length-diameter ratio

图7所示为不同长径比时水润滑轴承摩擦因数随转速的变化曲线。可以发现：长径比为1.5和2.5的轴承摩擦因数变化趋势与经典Stribeck曲线相符，摩擦因数随转速的升高先快速降低，进入弹流润滑状态后再缓慢增加。但长径比为0.5的轴承因一直处于混合润滑状态，摩擦因数一直下降。此外，在转速较低时增大长径比可减小轴承摩擦因数，但是当转速升高至1 600 r/min后，长径比为1.5的轴承摩擦因数开始小于长径比为2.5的轴承摩擦因数；而随着转速的进一步升高，在转速超过4 300 r/min后，长径比为0.5的轴承摩擦因数开始低于2种较大长径比的轴承摩擦因数，此时摩擦因数随长径比的增大而增大，但不同长径比的轴承摩擦因数差距很小。

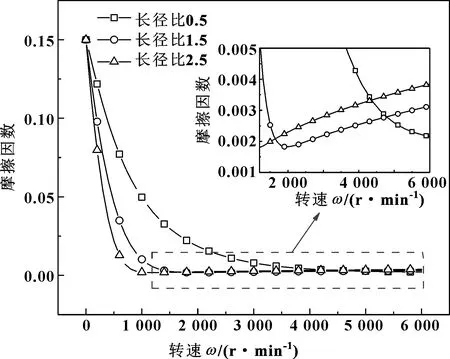
图7 不同长径比下摩擦因数随转速的变化Fig 7 Variation of friction coefficient with rotating speedunder different length-diameter ratio

上述摩擦因数随转速的变化规律可解释为：低速时，轴承处于混合润滑状态并且固体接触强度较大，此时增大长径比可改善轴承润滑状态(由图4可知)进而降低摩擦因数；随着转速的升高，当轴承润滑状态处于弹流润滑或者固体接触强度较弱的混合润滑状态时，水膜黏性剪切作用产生的剪应力对摩擦因数起主导作用，此时增大长径比会使轴承与水膜接触面积增加，导致产生更大的摩擦和拖力[23-24]，增大摩擦因数。

不同长径比时轴承最高温度随转速的变化如图8所示。可知，长径比为1.5和2.5时轴承最高温度随转速的升高呈现先迅速升高后降低，最后又缓慢升高的趋势。这是因为在转速较低时，轴承处于混合润滑状态，两表面粗糙峰的接触摩擦产生大量的热，并且摩擦功耗随转速的升高而增大，导致轴承温度迅速升高，并在转速为500 r/min时达到峰值；此后随着转速的进一步升高，水膜承载力随之增强，而固体接触强度逐渐减弱，故摩擦生热量逐渐降低导致轴承最高温度下降；当转速升高至起飞转速后，轴承进入弹流润滑状态，此时继续增大转速会导致更强的水膜剪切作用，逐渐增多的水膜剪切热量使轴承最高温度再次上升。而长径比为0.5的轴承在高速时未能进入弹流润滑状态，始终处于很弱的混合润滑状态，故轴承最高温度持续降低。此外，长径比为1.5和2.5的轴承最高温度变化曲线均存在一个极大值点和一个极小值点，意味着轴承运转过程中存在某一个转速使轴承温度最高，也存在某一个转速使轴承温度最低，在进行轴承设计时应尽量避免轴承长时间工作在使轴承温度最高的转速下。并且随着长径比的增大，轴承最高温度曲线的极大值与极小值点对应的转速值减小，同时轴承的最高温度也随长径比的增大而降低。

图8 不同长径比下轴承最高温度随转速的变化Fig 8 Variation of maximum temperature with rotatingspeed under different length-diameter ratio

为进一步分析长径比对轴承温度的影响，图9给出了转速为1 000 r/min时3种长径比的水润滑轴承与水膜交界面处的温度分布。可以看出，长径比为0.5时轴承温度最高，高温区域集中分布在轴承周向180°附近，最高温度在轴承两端面处。增大长径比后轴承最高温度降低，但轴承最高温度的分布面积增大，由周向180°附近位置向卷吸流动的上游扩展，并且最高温度位置由端面转向轴承中心。这是因为长径比增大后，轴承轴向长度的增加阻碍了水流端泄[6]，高温水流集中在轴承中心位置不能及时排出，并且随卷吸流动在轴承内部循环，导致轴承中心温度最高，并且几乎整个交界面均处于较高的温度。上述分析表明增大长径比后可使轴承温度降低，但对轴承高温水流的端泄具有阻碍作用，此外一旦有杂质颗粒进入轴承将很难通过端泄排出。

图9 长径比对轴承温度分布的影响Fig 9 Effect of length-diameter ratio on temperature distribution(a)L/Db=0.5;(b)L/Db=1.5;(c)L/Db=2.5

4 结论

(1)增大长径比可以增强水膜承载力，提高最小膜厚，降低轴承从混合润滑状态向弹流润滑状态转变的起飞转速，改善轴承润滑状态；小长径比的轴承非常有可能无法进入弹流润滑状态下工作。

(2)最大水膜压力与最大接触压力均随长径比的增大而减小，且水膜压力的周向峰值位置随长径比的增大向水膜发散区移动；增大长径比可均化水膜压力分布，削弱应力集中效果，延长轴承使用寿命；此外，长径比的增大会加快实现水膜承载的主体地位。

(3)低速时增大长径比可降低轴承摩擦因数，但升高转速使轴承润滑状态处于弹流润滑或者固体接触强度较弱的混合润滑状态时，摩擦因数随长径比的增大而减小。

(4)存在某一个转速使轴承温度最高，也存在某一个转速使轴承温度最低；增大长径比可降低轴承最高温度，但会导致轴承最高温度区域分布更广，最高温度位置由端面转向轴承中心；且大长径比对轴承水流的端泄具有阻碍作用，不利于杂质颗粒的排出。