轮缘润滑对列车曲线通过动态响应影响分析*

金泰木 张 涛, 展旭和 郭欣茹

(1.国家高速列车青岛技术创新中心 山东青岛 266111;2.西南交通大学牵引动力国家重点实验室 四川成都 610031)

重载铁路因具有绿色环保、投资少和效率高等优点，一直备受国内外货物运输的青睐，但在其运营服役过程中，诸多运行问题也被逐渐暴露出来。铁路曲线一直是铁路线路中三大薄弱环节之一[1]。当重载列车通过曲线时，车辆主要通过轮轨纵向蠕滑力来导向，同时会受到曲线超高、曲率以及离心作用力的影响；另一方面，为满足越来越高的运行速度和牵引力要求，目前重载电力机车均配置了大功率牵引电机，同时采用大轴质量的设计方式，这使得重载电力机车在通过曲线时轮轨动态作用力十分复杂，导致机车的轮轨系统的动力作用和磨耗加剧、列车的运行安全性降低，尤其是当施加牵引或制动力时。

针对重载电力机车曲线通过问题，国内外研究人员进行了诸多深入的研究。为提高机车导向转向架曲线通过能力，SIMSON和COLE[2-3]提出一种优化曲线通过时转向架摇头运动的控制策略，通过对比分析可知，该转向架具有良好的曲线通过性能。LIU等[4]通过建立详细的三维重载列车-轨道耦合动力学模型，分析了列车曲线通过时轮轨系统和钩缓系统的动态响应特性。毕鑫等人[5-6]分析了机车转向架曲线通过时的动态响应以及牵引力对机车曲线通过时轮轨蠕滑力响应的影响。杨亮亮等[7]对比分析了惰行和制动工况下列车曲线通过时的运行安全性、车轮踏面磨耗以及轮轨蠕滑特性的影响。曲天威等[8]对比分析了内燃机车采用径向转向架和传统转向架时通过曲线导向轮对内外侧车轮的黏着特性，并指出了径向转向架曲线通过的优势。刘鹏飞等[9]分析了轮对两侧不均衡闸瓦压力情况下重载机车曲线通过的动态行为特性。刘朝辉等[10]对比分析了惰行工况和压钩力作用下列车的曲线通过安全性。

采用轮缘润滑是减缓车轮轮缘磨耗的重要措施，但目前针对轮缘润滑对重载列车曲线通过性能的影响研究尚少。本文作者基于车辆-轨道耦合动力学理论，建立了重载列车-轨道三维耦合动力学模型，采用该模型分析了惰行和牵引工况下轮缘润滑对重载列车曲线通过轮轨系统动态相互作用的影响。

1 动力学仿真模型

轮轨系统动力学响应是分析重载列车曲线通过动态响应的重要参量。目前测试技术难以测得轮轨系统动态相互作用，尤其是轮轨切向相互作用。另一方面，与试验数据的对比验证结果证明动力学仿真技术拥有较高的精度。鉴于此，文中基于车辆-轨道耦合动力学理论[11]，建立了重载列车-轨道三维耦合动力学模型，部分仿真参数如表1所示。该仿真模型如图1所示，主要包含重载列车动力学模型、有砟轨道动力学模型和轮轨滚动接触模型。

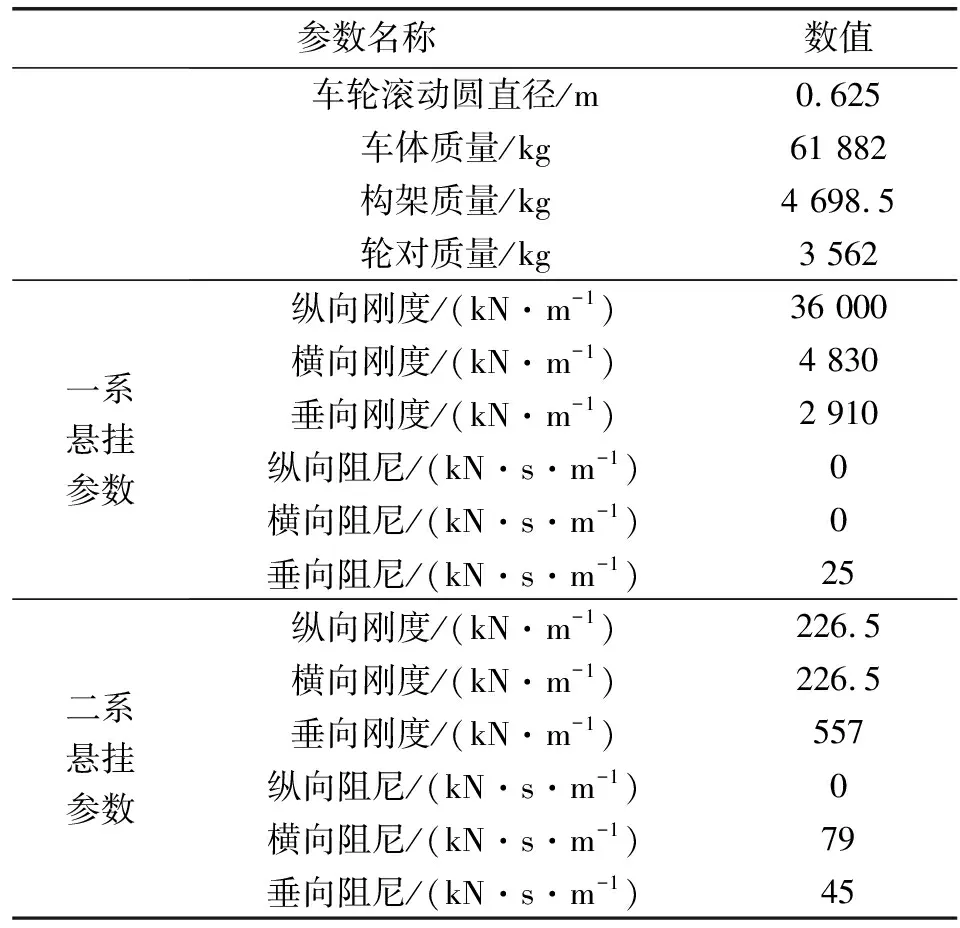
表1 机车车辆动力学模型主要技术参数

图1 重载列车-轨道耦合动力学模型Fig 1 Heavy-haul train-track coupled dynamic model (a) front view of the locomotive-track coupleddynamic model; (b) side view of heavy-haul train-track coupled dynamics model

1.1 重载列车和有砟轨道系统动力学模型

文中仿真模型中，重载列车的编组考虑为2节HXD1型电力机车和20节C80型货车。其中机车车辆系统由1个车体、2个构架、4个牵引电机和4个轮对组成。机车动力学模型中除牵引拉杆、牵引电机和旁承仅考虑部分运动自由度外，其余部件均考虑纵向、横向、垂向、侧滚、点头和摇头6个运动自由度。各部件间悬挂连接采用非线性弹簧阻尼单元或摩擦副单元模拟。此外，相邻车辆空间运动对其间的钩缓连接装置的缓冲器作用力以及车钩钩体空间运动姿态影响显著，在此将2个联挂车钩钩体视为一个整合的刚性体，忽略钩体间相对运动，考虑其除侧滚外的5个运动自由度，同时考虑缓冲器的非线性迟滞特性[4]。

有砟轨道模型由钢轨、扣件、轨枕和道床组成。其中钢轨模拟成连续弹性离散点支承的Euler梁，考虑其垂向和横向弯曲以及扭转振动，梁的边界条件为“简支-简支”；扣件系统用黏弹性弹簧-阻尼单元模拟；轨枕和道床均采用集总质量体模拟，其中轨枕考虑其横向、垂向和扭转振动，道床体仅考虑垂向振动。由于移动轨下支承模型更能真实地反映轮轨相互作用，尤其能精确地反映车轮通过枕跨时引起的周期载荷，同时可提高计算效率，因此文中采用文献[12]中的车辆-轨道激励模型。

需要说明的是，模型中对所有货车车辆均进行详细建模，但如若考虑所有车辆轮对作用下轨道系统的动力学响应，则会造成轨道计算长度过长，严重降低仿真计算效率。由于文中重点关注机车的轮轨系统动态相互作用，因此模型中仅考虑机车车轮作用下轨道系统的动力学响应，忽略了所有货车车辆所对应的轨道系统的振动响应。

根据达朗伯原理，可推导得到车辆悬挂系统、扣件系统和轨枕道床作用力，以及列车和轨道系统的运动平衡方程。由于系统作用力的求解方程过于繁琐，限于篇幅在此不再给出。列车和轨道系统的运动平衡方程可表示为

(1)

1.2 轮轨滚动接触模型

轮轨滚动接触模型是联结列车系统模型和轨道系统模型的枢纽，主要包含轮轨空间接触几何关系、轮轨法向力以及轮轨蠕滑力(矩)的求解。文中建立了考虑多点接触的轮轨滚动接触模型，同时考虑轮缘润滑对轮轨蠕滑特性的影响。

1.2.1 轮轨空间接触几何关系

在求解轮轨法向力和轮轨蠕滑力之前，首先需求解轮轨空间接触几何关系，其中机车轮轨空间接触几何关系如图2所示。

图2 机车轮轨空间接触几何关系Fig 2 Space contact geometry of locomotive wheel and rail

文献[13]提出了一种可用于轮轨多点接触求解的迹线极值法，但该方法基于左右侧轮轨不分离的假设，通过不断迭代轮对侧滚角来获得轮轨空间接触点位置。文中模型对该方法进行了修正，可处理轮轨分离现象而不需要迭代轮对侧滚角。轮轨空间接触几何关系计算主要包含4个步骤：

(1)利用迹线法[14]求得轮轨踏面上可能的一系列离散点。在此应保证轮轨离散点横坐标相同，可首先获取车轮踏面离散点，然后通过车轮踏面离散点向钢轨廓形插值得到钢轨的离散点。

(2)求解笛卡尔坐标系中各个离散点对应的轮轨垂向分离量，其中i点处轮轨垂向分离量S(yi)为

S(yi)=zw(yi)-zr(yi)

(2)

式中：yi为离散点横向坐标，zw(yi)和zr(yi)分别为轮轨踏面离散点垂向坐标。

(3)求解垂向分离量S(yi)关于横向位置的一阶导S′(yi)和二阶导S″ (yi)，只有极小值点才可能成为潜在的轮轨接触点。判断准则为

(3)

式中:k为极小值点编号;Nmin为极小值总个数。

(4)若需进一步判断轮轨接触点，求解得到轮轨垂向间隙的极值点后，还需结合轮轨接触点位置和对应的轮轨压缩量做进一步判断：

(4)

式中:δk为各极值点对应的轮轨垂向压缩量;Δyk为相邻两极值点的踏面弧线间距;εd为限定相邻2个极值点不会因为过于靠近而形成一个接触点的临界值，在此取为10 mm。

1.2.2 轮轨法向力和蠕滑力

对于各个轮轨接触点，文中采用Hertz非线性弹性接触理论计算轮轨法向力：

(5)

式中:KHertz为轮轨赫兹接触刚度;δwr为轮轨法向压缩量。

由于Polach理论可较好地处理大蠕滑情况下的轮轨黏着特性，因此文中各接触点的轮轨蠕滑力采用Polach蠕滑模型求解[15-16]。大量实验和理论研究结果表明，轮轨低黏着接触条件或过大的牵引/制动载荷等因素会导致轮轨相对滑动量增大以及轮轨摩擦因数降低，因此文中轮轨蠕滑力计算模型中考虑变摩擦因数：

μ=μ0[(1-Ap)e-Bp w+Ap]

(6)

式中:μ0为静摩擦因数;w为轮轨相对滑动速度;Ap和Bp分别为动摩擦因数(微滑趋于无穷时)和静摩擦因数之比和指数型摩擦因数衰减系数。

轮轨蠕滑力以及纵向和横向的分量可根据式(6)—(8)计算。

(7)

(8)

(9)

式中：a和b分别为轮轨接触斑长半轴和短半轴，可根据Hertz接触理论计算得到；C为Kalker蠕滑系数；s为轮轨蠕滑率；sx和sy分别为纵向蠕滑率和横向蠕滑率；kA和kS为衰减因子。

此外，Polach理论不能求解轮轨蠕滑力矩，在此利用沈氏理论求解。上述各式中Ap、Bp、kA、kS和μ0与轮轨接触条件有关，列于表2。

表2 轮轨接触参数

图3示出了低速和高速时，不同接触条件下的轮轨黏着特性曲线。可以看出，随着轮轨蠕滑率的增大，轮轨摩擦因数逐渐减小。轮轨黏着系数始终低于摩擦因数，其中低速时干燥状态和脂润滑状态对应的最大轮轨黏着系数分别为0.460和0.094，高速时干燥状态和脂润滑状态对应的最大轮轨黏着系数分别为0.400和0.090。随着轮轨蠕滑率的增大，轮轨黏着系数逐渐逼近摩擦因数。此外，干燥状态下轮轨摩擦因数及黏着系数大于脂润滑状态条件下的摩擦因数和黏着系数。

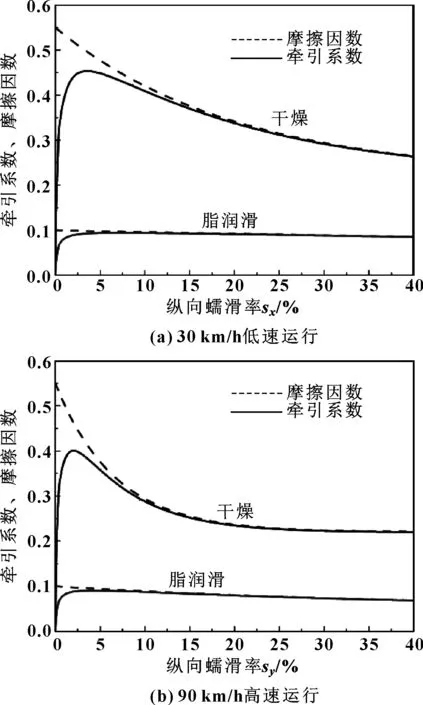
图3 轮轨黏着特性曲线(116 kN)Fig 3 Wheel-rail adhesion characteristic curves (116 kN)(a)low speed operation of 30 km/h;(b)high speed operation of 90 km/h

1.3 重载列车动力学模型验证

通过对比现场测试和仿真计算获得的轴箱振动特性，验证了所建立的重载列车-轨道耦合动力学模型的准确性。图4示出了现场测试和仿真得到的轴箱垂向振动加速度曲线。其中仿真计算工况和实际运行工况设置为一致，曲线半径为400 m，曲线超高为100 mm，列车运行速度为58 km/h。可以看出，仿真计算所得的轴箱垂向振动加速度略小于实测所得轴箱垂向振动加速度，这可能是由于忽略了车辆结构的柔性效应，同时未考虑线路不平顺的影响。但总体而言，仿真计算所得的轴箱垂向振动与实际测试结果吻合较好，因此可认为该模型可用于轮缘润滑对重载列车曲线通过性能的影响研究。

图4 实测和仿真轴箱垂向振动加速度比较Fig 4 Comparison of vertical vibration acceleration ofaxle box by test and simulation

2 计算结果及分析

利用上述建立的重载列车-轨道三维耦合动力学模型，系统地分析了惰行和牵引工况下轮缘润滑对重载列车曲线通过时轮轨系统动态相互作用的影响。正常情况下，车轮轮缘润滑区域和踏面不同横向位置处静摩擦因数如图5所示。仿真中，为避免踏面干燥区域和润滑区域交界处摩擦因数的突变而导致轮轨动力作用数值计算结果出现跳跃现象，文中在该位置附近设置一段较小的过渡区域，在该区域内对轮轨接触参数进行线性化过渡处理。

图5 轮缘润滑区域及踏面不同位置处摩擦因数Fig 5 Friction coefficient of wheel flange lubrication areaand different positions on wheel tread

文中仿真计算，重载列车运行速度为64 km/h，线路曲线半径和超高分别为400和100 mm，其中直线段、缓和曲线段和圆曲线段长度分别为50、50和100 m。未考虑轨道随机不平顺的影响。牵引工况下，机车车辆施加的牵引载荷为40 kN·m。需要说明的是，为了保证列车在驱动工况下以恒定速度通过曲线，在牵引工况中于最后一节货车车尾施加大小等同于总牵引力的反向车钩力，未考虑基本运行阻力和线路阻力的影响。文中着重分析一位机车导向轮对的动力学响应。

轮对在通过曲线时，主要依靠内外侧的轮轨纵向蠕滑力所形成的力矩进行导向，即为轮对导向力矩，此力矩越大则轮对导向能力越强。图6和图7所示分别为惰行工况和牵引工况下有无轮缘润滑时的轮轨纵向蠕滑力。可以看出，当机车轮对通过缓和曲线区间时，内侧轮轨出现多点接触现象；而当通过圆曲线区间时，外侧轮轨出现多点接触现象。惰行工况下，内外侧轮轨纵向蠕滑力方向相反。当无轮缘润滑的机车轮对在圆曲线上运行时，外侧2个轮轨接触点的纵向蠕滑力分别为9.25和13.74 kN，内侧轮轨纵向蠕滑力为23.40 kN；而当有轮缘润滑的机车轮对在圆曲线上运行时，外侧2个轮轨接触点的纵向蠕滑力分别为10.56和3.20 kN，内侧轮轨纵向蠕滑力为14.11 kN。牵引工况下机车轮对通过圆曲线时，内外侧轮轨纵向蠕滑力变化方向相反。当无轮缘润滑时，外侧2个轮轨接触点的纵向蠕滑力分别为20.05和18.76 kN，内侧轮轨纵向蠕滑力为24.50 kN；而当存在轮缘润滑时，外侧2个轮轨接触点的纵向蠕滑力分别为28.32和3.07 kN，内侧轮轨纵向蠕滑力为31.06 kN，此时内外侧轮轨纵向蠕滑力的差值几乎为0。上述分析结果表明，轮缘润滑对机车轮轨动态相互作用影响显著，相比于无轮缘润滑，当机车轮对通过小半径圆曲线时，惰行和牵引工况下的外侧轮缘位置处的轮轨纵向蠕滑力均明显降低，其中牵引工况下内外侧轮轨纵向蠕滑力的差值明显低于惰行工况下的内外侧轮轨纵向蠕滑力差值。由此说明轮缘润滑作用显著削弱了轮对的导向能力，尤其是在牵引工况下。

图6 惰行工况下轮轨纵向蠕滑力Fig 6 Longitudinal creep force of wheel and rail during idlingcondition (a) without wheel flange lubrication;(b) with wheel flange lubrication

图7 牵引工况下轮轨纵向蠕滑力Fig 7 Longitudinal creep force of wheel and rail during tractioncondition (a) without wheel flange lubrication;(b) with wheel flange lubrication

图8所示为惰行工况和牵引工况下有无轮缘润滑时的轮对横移量和冲角历程响应。可以看出，在惰行工况和牵引工况下，当机车轮对在缓和曲线区间内运行时，轮对横移量和冲角随着曲线曲率的增大而增大，此时外侧出现了车轮踏面和轮缘2个位置处的轮轨接触点。惰行工况下，存在轮缘润滑时的轮对横移量略大于无轮缘润滑时的轮对横移量；而牵引工况下轮缘润滑作用则对轮对横移响应影响不大，当机车轮对在圆曲线上运行时，2种情况下轮对横移量均约为9.71 mm。相比于轮对横移量，轮缘润滑作用对轮对冲角响应影响更为显著，惰行工况和牵引工况下，当机车轮对在圆曲线上运行时，有轮缘润滑时的轮对冲角明显大于无轮缘润滑时的轮对冲角。轮轨纵向蠕滑力与轮对冲角的关系可解析地表示为

图8 不同工况下轮对横移量和冲角Fig 8 Lateral displacement and impact angle of wheelset underdifferent conditions (a) idling condition;(b) traction condition

(10)

式中:下标i=1,2分别表示左右侧轮轨;f1为蠕滑系数;l0表示轮对中心到车轮名义滚动圆的横向距离;ri表示车轮瞬时滚动圆半径;r0为车轮名义滚动圆半径;ψw表示轮对冲角。

根据式(10)可知，当轮对通过曲线区段时，轮轨纵向蠕滑力随着轮对冲角的增大而减小，使得轮对导向能力减弱。由此进一步说明，轮缘润滑作用会抑制轮对的导向能力。

图9所示为惰行工况和牵引工况下有无轮缘润滑时的一位车钩摆角和二位车钩摆角历程响应。可以看出，当重载列车进入曲线区段时，二位车钩的摆角明显大于一位车钩的摆角。当在圆曲线区段运行时，惰行工况下二位车钩的摆角为1.5×10-4～2.0×10-4rad，而牵引工况下二位车钩的摆角为3.0×10-4～3.5×10-4rad。此外，无论惰行还是牵引工况下，有无轮缘润滑作用时车钩摆角相差很小。由此说明，牵引载荷对车钩空间运动影响较大，而轮缘润滑作用对其影响微小。

图9 不同工况下有无轮缘润滑作用时一位和二位车钩摆角Fig 9 Swing angle of one and two position couplers under differentworking conditions with or without rim lubrication(a)idling condition;(b)traction condition

3 结论

基于车辆-轨道耦合动力学理论，建立重载列车-轨道三维耦合动力学模型，系统地分析惰行和牵引工况下对重载列车曲线通过性能的影响。主要得出以下结论：

(1)轮缘润滑对机车轮轨动态相互作用影响显著。相比于无轮缘润滑，当机车轮对通过小半径圆曲线时，外侧轮缘位置处的轮轨纵向蠕滑力明显降低，惰行和牵引工况下内外侧轮轨纵向蠕滑力的差值均较有轮缘润滑作用时减小，由此说明轮缘润滑作用会削弱轮对的导向能力，尤其是在牵引工况下。

(2)轮缘润滑对轮对横移运动影响不大，而对轮对冲角响应影响更为显著。惰行工况和牵引工况下，当机车轮对在圆曲线上运行时，有轮缘润滑时的轮对冲角明显大于无轮缘润滑时的轮对冲角。

(3)牵引载荷对车钩空间运动影响较大，而轮缘润滑作用对其影响微小。