风力机与液力变速传动装置匹配工作特性研究

董 泳 周绪强 毕 强

1.哈尔滨工业大学，哈尔滨，150001 2.中国石油管道公司，廊坊，065000

3.沈阳发动机设计研究所，沈阳，110015

0 引言

目前，大型风力发电机组几乎都采用变速风力机，这是由风速的不稳定性和最大风能捕获原理决定的［1］。并网型风电机组的输出电功率须满足恒频、恒压的并网要求，需要一个中间环节来实现“变速”与“恒频”之间的转化，这个中间环节采用了电力电子技术的逆变装置，主流技术为双馈感应发电机和永磁无齿箱直驱同步发电机的风力发电系统。

近年来，有研究者提出各种用于风电系统的新型传动形式以取代整流逆变装置，以实现与常规燃油、燃气或燃煤电厂相似的直接并网发电。其基本思想是在风力机和发电机之间连接一台可调节的传动装置，当风力机转速在一定范围内变化时，发电机的输入转速保持恒定。目前已实现商业化运行的是采用德国伏伊特（Voith）公司WinDrive装置的风力发电系统。

1 变化的风轮转速到恒定的发电机输入转速

图1所示为一种典型的采用逆变方式的变速恒频风力发电机组［2］。与同步发电机和交流／直流／交流逆变器组成的变速恒频发电系统相比，双馈感应发电机系统的电力变换装置处在发电机的转子回路（励磁回路），容量较小，适合于大型变速恒频风电系统。

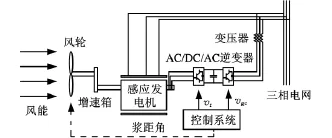
图1 采用逆变装置的变速恒频风力发电系统［2］

我国大型并网风力发电机组的研制与生产已进入兆瓦级的规模，整流逆变装置应用广泛。单机容量的不断增大，对大功率整流逆变系统也提出了更高的要求，同时风电厂商也要负担更高的初次投入成本，即使是直驱的发电方式也离不开大功率的整流逆变装置。

变化的风轮转速到恒定的发电机输入转速可以采用二自由度差动轮系与伺服电机配合调速的传动系统［3］来实现，如图2所示。差动轮系任意两轴转速合适的组合即可决定第三轴的速度。通过伺服电机调节太阳轮的转速以适应行星架转速的变化来控制齿圈输出转速，可使发电机的转速保持恒定。此类系统需要大扭矩、宽转速调节范围的伺服电机，成本会很高；如果伺服电机作为发电机工作时，发电并网同样需要整流逆变装置。伺服电机也可以用液压泵或马达来替代，但也同样面临大功率液压元件的选型问题。

图2 应用伺服电机调速的变速恒频传动系统

图3所示为一种采用液力变速与传动装置（以下简称“液变装置”）的风力发电系统［4］。液变装置基本组成为一套叠加的行星变速箱和一台导叶可调式液力变矩器，如图4所示。

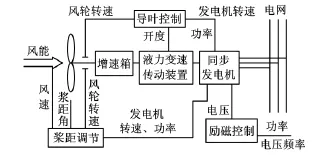
图3 采用液力变速传动装置的风力发电系统

图4 WinDrive—— 液力变速与传动装置［4］

伏伊特公司于2003年提出“风电液变驱动”的概念，2006年将其应用于DeWind公司的D8.2风力机［5］，装置命名为“WinDrive”。此种风力发电系统中，可调式液力变矩器的主要功能是配合行星齿轮系，以适应不断变化的风轮转速，利用分流的部分功率实现变化的风轮转速到同步发电机转速的恒定输入，从而保证发电机输出电压与频率的稳定而不必附加其他大功率逆变装置。

液变装置应用于大型风力发电机组综合了传统的液力元件能容与功率重量比大、隔离衰减扭振、涡轮输出的自动适应性、使用可靠、寿命长等多项优良的传动品质与特点，能够满足宽风轮转速变化范围的电网质量要求和并网所需条件，并且具有与采用逆变方式的风电系统可比拟的发电效率［6］。

2 风力机与液变装置匹配的基本关系

2.1 变化的风轮转速到恒定的发电机输入转速

采用液变装置的风力发电系统具有图5所示的运动关系，图中，液力变矩器中的B代表泵轮，T代表涡轮，D代表导轮。

图5 液变装置的运动关系

根据图5所示的啮合关系，差动轮系传动机构的3个构件以及与它们相连的3个轴上的转速满足以下运动学方程：

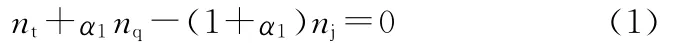
其中，nt、nq、nj分别为太阳轮、齿圈、行星架的转速；α1为差动轮系的结构参数。太阳轮的转速同时也是液力变矩器的泵轮输入转速（nB）和发电机的输入转速（nG）。

风轮转速与行星架转速之间的关系为

式中，nR为风轮转速；α3为增速箱传动比。

通过定轴轮系，液力变矩器涡轮输出转速nT与齿圈转速nq的关系为

式中，α2为定轴轮系结构参数。

将式（2）、式（3）代入式（1），nt用nB或nG代替，经过整理，得到变化的风轮转速与恒定的发电机输入转速、涡轮输出转速与风轮转速的匹配关系：

由式（4）可以进一步得到适应某一风轮转速变化范围（nR1～nR2，nR2＞nR1）的液力变矩器对应的工况转速比iTB＝nT／nB的一些重要关系。

高风轮转速对应低转速比：

低风轮转速对应高转速比：

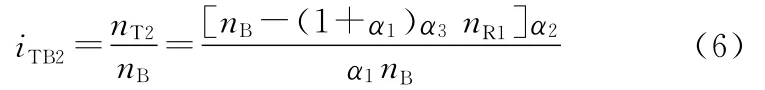
对应转速比范围比例带：

差速比关系：

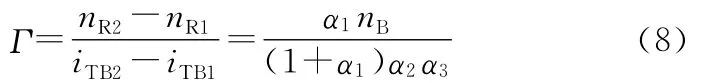
2.2 液力变矩器泵轮的输入功率

对于图5中的差动轮系传动机构，3个构件与它们相连的3个轴上的转矩存在如下关系：

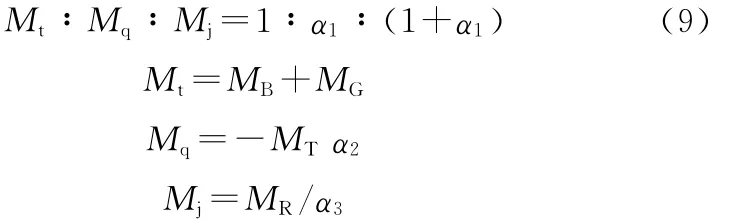
式中，MB为液力变矩器泵轮输入转矩；MG为发电机输入轴转矩；MT为液力变矩器涡轮输出转矩；MR、Mt、Mq、Mj分别为风轮转矩、太阳轮转矩、外齿圈转矩、行星架转矩。

根据式（9）中的转矩比例关系，可以得到液力变矩器涡轮输出转矩与风轮转矩间的关系：

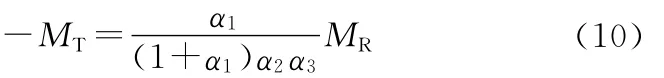
由式（4）可得涡轮输出转速：

则涡轮输出功率为

式中，ωT为涡轮旋转角速度。

参照液力变矩器的原始特性，得到对应工况点液力变矩器的传动效率η，由此可以确定泵轮输入功率：

结合式（10），考虑到泵轮与涡轮转矩间的变矩关系，可得泵轮功率占风轮功率的比例：

式中，ωB为泵轮旋转角速度；ωR为风轮旋转角速度；K为液力变矩器的变矩系数，K＝－MT／MB，并且有η＝KiTB。

结合式（8），式（14）可写成

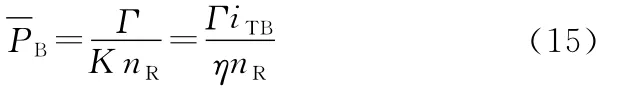
随着风轮转速的增大，系统调节液力变矩器涡轮的输出转速是降低的，转速比向减小的方向移动，根据液力变矩器的原始特性，变矩系数K呈增大的趋势。因此，由式（15）可以看出，随着风轮转速的提高，风轮功率增加，对于一定的差速比Γ，液力变矩器取自风轮功率的比例是逐渐减小的。

2.3 匹配风力机工况的液力变矩器的输出特性

在掌握风轮转速—转矩特性的条件下，根据式（10）和式（11），可以确定对应风轮取得最佳功率工况点（由风力机最大风能捕获原理确定）的变矩器工作点参数。

图6 WinDrive装置工作特性曲线［6］

变矩器涡轮输出转矩与风轮转矩是标准的比例关系，而涡轮转速与风轮转速的关系则是一条负斜率直线的关系，即随着风轮转速的增大，风轮转矩增大，而液力变矩器涡轮输出转速则是降低的，涡轮输出转矩也是增大的，液力变矩器适应风轮工作的这种特征正是液力变矩器本身自动适应性的体现。

WinDrive的工作原理是基于一台液力变矩器和与之相连的一套叠加行星齿轮，作为流体机械，液力变矩器的输出特性与风轮转子转矩—转速特性相吻合，因此，将两者配合起来使用是再理想不过的了［4］。同时也不难理解，在图6所示的WinDrive工作特性曲线中，在某一风轮转速变化范围内，变矩器工作在某一固定导叶开度附近就可以满足系统工作要求。

可以设想，通过良好的匹配设计，在实际工作中，在某个转速比工况范围内，依靠液力变矩器本身的固有特性或者只需导叶开度作微小的调节即可实现变化的风轮转速的跟踪匹配。即使在较大的对应风轮转速的变化范围内，导叶开度也只需要做一定的开度范围的动作即可满足调节要求，而变矩器的效率并不因为导叶开度的变化而出现明显的降低。

3 液变装置的总体传动效率

3.1 基于功率分流原理的总体传动效率

根据图5所示的动力传输关系，采用液变装置的风电系统符合图7所示的功率分流原理。

图7 液变装置的功率分流原理

叠加行星齿轮变速箱功率的输入与输出满足以下能量平衡方程：

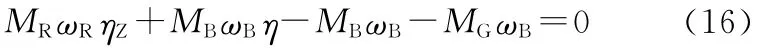
式中，ηZ为增速箱的机械传动效率。

由此可计算液变装置的输入到发电机输出的总体传动效率：

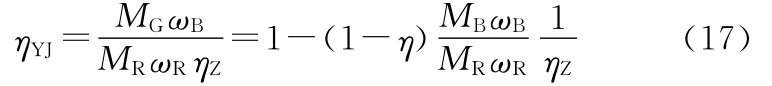
结合式（14），式（17）可写成

可以看出，在机械传动装置结构参数（α1、α2、α3）一定的条件下，液变装置的传动效率与液力变矩器的效率特性有很大的关系。通常情况下，差动轮系结构参数α1的合理取值范围为1.33～4，α1的取值一般不超过5［7］；定轴轮系结构参数α2的合理取值范围为2～8［8］。

3.2 液变装置传动效率的影响因素

对于变速风力机技术要求给定的最大和最小风轮转速变化范围nRmin～nRmax及设计风轮转速nR，de，推荐的一种匹配方式是保证常见风轮转速工况范围（n′R1～n′R2）对应的液力变矩器转速比在高效区范围内。根据实际的风力机运行情况，若超过设计风轮转速，风力机将进入功率限制状态，因此，可将常见风轮转速范围控制在低于设计风轮转速的某个区间，即n′R1＜n′R2≤nR，de。为了获得较高的总体传动效率，将常见的低风轮转速n′R1对应取得变矩器的设计工况转速比i＊TB，即对应变矩器的最佳效率工况。

下面结合图8所示典型的离心涡轮导叶可调式液力变矩器的原始特性，针对关键结构参数对系统匹配工作性能的影响给予定性分析，由此说明确定系统结构参数的某些原则。

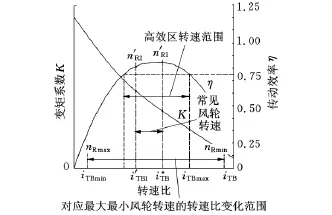
图8 适应风轮转速变化的变矩器转速比工况

（1）对应最大风轮转速nRmax的涡轮输出转速受到液力变矩器零速工况的限制，也就是说，极限情况液力变矩器处于制动工况，即nTmin＝0。由式（11）可得

由此可以得到差动轮系结构参数：

（2）确定常见风轮转速区间的下限n′R1对应液力变矩器的设计工况转速比i＊TB，根据风轮转速对应变矩器转速比的关系（式（6））可得

差动轮系结构参数α1一旦确定，定轴轮系结构参数α2也随之确定。由此得到

由上式可以看出，在对应设计工况点转速比较大的情况下，α2较大。α1增大，α2也增大，并且α2增大的幅度相对更大一些。

（3）对式（22）作如下变换：

可将式（8）的差速比Γ写成另一种形式：

由上式可明显看出，α1增大，差速比Γ减小。

对应n′R1～nRmax，差速比Γ可表示为

对应nRmin～n′R1，差速比Γ可表示为

由式（25）和式（26）可以看出，随着α1的增大，差速比Γ减小，对应最大风轮转速的变矩器最小转速比iTBmin减小，而对应最小风轮转速的变矩器最大转速比iTBmax增大，即对应全风轮转速变化范围的变矩器对应的转速比工况区间增大；随着α1的减小，这个区间收窄。

从图8可以看出，α1增大，对于高于n′R1的风轮转速区，工况左移，差速比Γ减小，而液力变矩系数K则增大，泵轮取自风轮的功率比例呈减小的趋势，有利于高风轮转速区总体传动效率的改善；对于低于n′R1的风轮转速区，虽然差速比Γ减小，但由于转速比工况的右移，变矩器的K和η值均呈下降的趋势，总体上会使低风轮转速区的传动效率变低。

在实际的风力发电系统中，一般较为重视接近设计风轮转速区的总体传动效率，所以α1还是应尽量取得大一些。但这样会使接近风轮最大转速nRmax时，在液力变矩器接近制动工况的区域，液力变矩器传动效率较低，发热量较大，需要重点关注变矩器的循环冷却问题。另外，还要综合考虑高转速比工况特性的限制以及结构尺寸变大的问题。

（4）以上分析是在增速箱传动比α3一定条件下做出的。在常见风轮转速区间n′R1～n′R2对应的液力变矩器转速比工况i′TB1～i′TB2（i＊TB）确定的情况下，α3的取值不影响转速比iTB、泵轮功率比例和总体传动效率ηYJ。

由式（24）可得

由上式可以看出，α3增大，α1是减小的，同样α2也是减小的；α3减小，情况则相反。在此种情况下，α3的变化只涉及增速箱和液变装置尺寸、重量的匹配问题。过大的α3则受到液变装置差动轮系结构参数和最高风轮转速的限制，根据α1合理的结构参数的下限值1.33，由式（20）可得

作为一个算例，D8.2风力机风轮转速变化范围为11.1～20.7r／min，取nRmax＝20.7r／min，nB＝1500r／min，由式（28）可得α3≤31。

如果没有预先确定常见风轮转速区间对应的变矩器转速比工况，α3的变化同样会使风轮转速范围对应变矩器转速比工况范围加大或收窄，α3应取一个较为合适的值。

4 液变装置与风力机匹配计算实例

采用逆变方式的风力发电系统（图1），除了发电机以外的传动设备总体传动效率满负荷工况估算为：0.985（增速箱效率）×0.97（逆变器效率）×0.99（变压器效率）＝94.59%。相比而言，采用液变装置的风力发电系统发电机前传动设备的传动效率在设计风轮转速工况或其附近也应达到这个水平。以下匹配计算则以此为参考目标，并参照WinDrive装置得以应用的DeWind D8.2风力机技术参数（表1）。

表1 DeWind D8.2风力机技术参数［9］

4.1 与低转速比变矩器的匹配计算

从图4所示的WinDrive装置的剖面图可以看出，液变装置采用的是两级涡轮的双级液力变矩器。多级液力变矩器可获得比单级液力变矩器更大的起动变矩系数K0，同时可扩大高效区的工作范围，但最高效率略低，这两个重要特点适合于风力发电系统变速与传动的应用。大型风力机风轮转速较低，风轮转矩较高，在同等循环圆直径下，多级变矩器涡轮具有较高的力矩输出能力，占有结构方面的优势；较宽的高效区范围则适应风力机宽范围的风轮转速的变化。

多级液力变矩器在国内应用较少，更没有导叶可调式的水力模型可供参考。叶型资料、特性数据较为全面的是曾经用于内燃机车的NY5起动型液力变矩器［10］，其导叶不可调，设计工况转速比i＊TB＝0.35，最高效率ηmax接近77%，为典型的低转速比应用类型的变矩器，其原始特性曲线如图9所示。虽然没有部分导叶开度下的特性，但借助现有的实验数据，针对双级低转速比变矩器的匹配计算结果仍然具有一定的参考价值。

匹配结果（计算过程略）见表2：差动轮系结构参数α1＝1.80；定轴轮系结构参数α2＝2.32；增速箱传动比α3＝25。

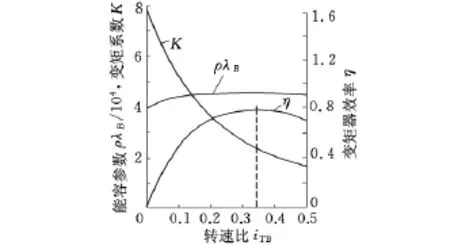
图9 NY5起动型变矩器原始特性曲线

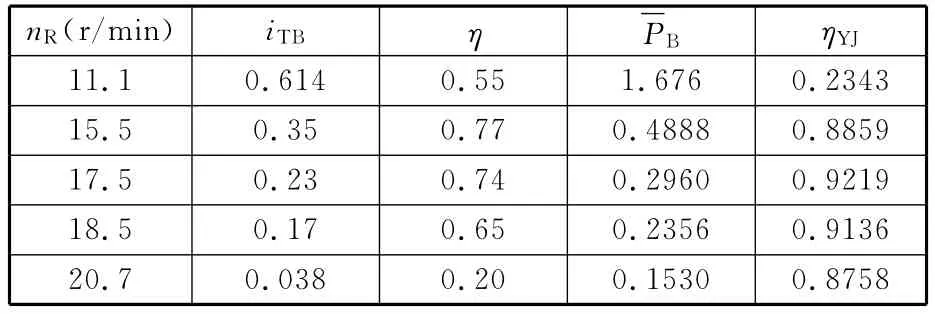
表2 采用NY5起动型变矩器的匹配计算结果

对应液力变矩器工况点的效率偏低，与参考传动效率的目标值存在一定的差距。我国在导叶可调式液力变矩器水力模型的基础研究工作方面相对比较薄弱，NY5起动型变矩器的特性可以说处于20世纪80年代的水平。试想，通过优化设计，该种型号的变矩器的效率能够达到一般液力变矩器的通用水平（最高效率84%～85%），在整个风轮转速变化区间内，可以获得较为理想的匹配结果。按初步匹配计算的数据，针对2MW风力机，设计风轮转速工况液力变矩器泵轮输入功率约为500kW，对于液力传动元件尚属于低功率等级，但对于伺服电机或者液压马达，就目前水平而言，则具有相当大的难度。

4.2 与高转速比变矩器的匹配计算

LB46型变矩器为导叶可调式液力变矩器［10］（单级涡轮结构），设计工况转速比i＊TB＝0.92，最高效率ηmax接近85%，为高转速比应用类型的液力变矩器，其原始特性曲线如图10所示。

图10 LB46型变矩器原始特性曲线

匹配结果（计算过程略）见表3：差动轮系结构参数α1＝1.8；定轴轮系结构参数α2＝6.0；增速箱传动比α3＝25。

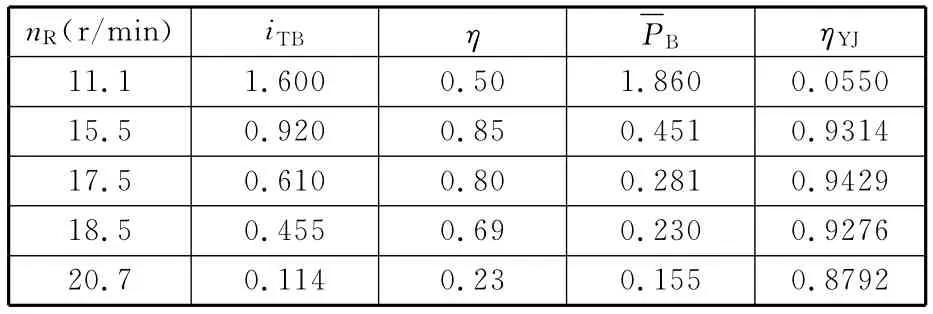
表3 采用LB46型变矩器匹配计算的结果

初步的匹配计算表明，在常见的风轮转速范围（15.5～18.5r／min）内，直到最大风轮转速，采用LB46型变矩器可以得到较为理想的匹配结果。但由于LB46型变矩器高转速比工况相对偏低的传动效率，导致对应低风轮转速工况很低的液变装置传动效率。如果最低风轮转速对应更大的变矩器转速比则会给匹配设计带来困难，或者说，低风轮转速工况变矩器特性不可用。另一方面，相对双级变矩器，行星变速箱定轴轮系传动比较大，用在风力发电系统的吊舱中，尺寸、重量方面存在劣势。

离心涡轮液力变矩器一般为不透穿或具有一定的负透穿性。变矩器泵轮（包括发电机）作为差动机构太阳轮的负载，其共同工作特性的分析比较复杂。但总体来说，用于风力发电系统变矩器的共同工作输入特性与常规应用的作为柴油机或电动机负载的泵轮工作状况并无太大的区别。

5 结论

（1）可调式液力变矩器与叠加的行星变速箱组成的复合传动装置适合于大型风力发电机组的应用，能实现变化的风轮转速到恒定的发电机输入转速。

（2）常见的风轮转速变化区间对应基型变矩器高效转速比工况的匹配方法在概念上是比较明确的。匹配设计的目标是保证常见风速工况达到较高的总体传动效率，兼顾接近最大、最小风轮转速的匹配工作特性，同时要综合考虑机械结构设计的合理性。

（3）低转速比型号的液力变矩器更适合于风力机吊舱中的应用，获得性能良好的低转速比水力模型是一项重要的基础研究工作。

［1］Tony Burton.风能技术［M］.武鑫，译.北京：科学出版社，2007.

［2］董泳，王洪杰，周绪强.风力发电系统液力变速与传动应用技术研究［J］.热能动力工程，2008，23（6）：670－675.

［3］Zhao Xueyong，Maiber P.A Novel Power Splitting Drive Train for Variable Speed Wind Power Generators［J］.Renewable Energy，2003，28（13）：2001－2011.

［4］Voith Turbo.WinDrive—the Innovative Drive Concept for Wind Energy Plants［EB／OL］.［2010－02－22］.http：／／www.voithturbo.com／sys／php／docdb＿stream.php？pk＝1768.

［5］Detlef Koenemann.It’s Possible without［J］.Sun ＆Wind Energy，2009（5）：216－218.

［6］Voith Turbo.Project Report 2010［EB／OL］.［2010－02－25］.http：／／www.voithturbo.com／media／Projectreport＿BARD＿Zwischenbericht＿en.pdf.

［7］朱经昌，魏辰官，郑慕侨，等.车辆液力传动（上册）［M］.北京：国防工业出版社，1982：189－190.

［8］张展，张弘松，张晓维.行星差动传动装置［M］.北京：机械工业出版社，2009：3－4.

［9］DeWind.DeWind D8.2Technical Brochure［EB／OL］.［2008－07－08］.http：／／www.compositetechcorp.com.

［10］北方交通大学.内燃机车液力传动［M］.北京：中国铁道出版社，1980：78－89.