基于近似模型管理的微小卫星结构多目标优化设计

郑 侃 廖文和 张 翔

南京航空航天大学，南京，210016

0 引言

微小卫星结构设计属于复杂而庞大的系统工程，设计变量多，制约因素苛刻，通常存在多个相互冲突的目标函数，并且由于在优化过程中必须反复迭代分析模块，造成优化过程中的计算量较大且容易陷入僵局，严重影响了优化效率和结果。为此，研究人员就多目标优化算法的实现、优化模型的建立、近似技术的运用、非劣解集的筛选等方面展开了细致而深入的研究，特别是在优化算法的改进和近似技术的运用两方面取得了较大的进展，对于提升优化效率起到了举足轻重的作用。Coello等［1］和 Hu等［2］在粒子群优化算法的基础上分别提出了一些具有较大影响力的研究成果，例如一类特别变异的算子、采用外部集合保存非支配粒子集的方法以及动态邻居的粒子群算法等。于广滨［3］将改进的双群体差分多层文化粒子群融合算法应用于微型减速装置的多目标优化中，不仅实现了群体的多样性还提高了算法的收敛速度；安治国等［4］比较了各种构建近似模型方法的优缺点，并提出了用于板料成形的径向基函数近似模型方法。

近似技术的应用在很大程度上加快了演化算法的寻优速度，但受到样本数量以及工程问题本身高维性的限制，近似模型的精度通常很难得到保障，特别是对于航空航天领域非线性程度较高的复杂问题就更加棘手。为此，近似模型管理框架的概念应运而生，其中，一种方式是在演化过程中选取合适的修正点逐步对近似模型进行修正，实现对近似模型的管理；而另一种方式则是从搜索区域更新方向着手，根据信赖度的大小对搜索区域进行缩放，从而确保能够获取足够精度的非劣解。本文从优化实例自身的特点出发，在基于信赖域的近似模型管理的基础之上，通过最大最小距离策略从每一步迭代过程中选取合适的非劣解用于计算信赖度值，确保对信赖域更新的合理性，从而使得在多目标优化求解过程中得到较高精度的最优解。

1 多目标优化中的近似技术

近似技术常用于处理几个独立变量影响一个或多个因变量且函数关系未知的较为复杂的工程问题，主要是用显式近似表达式来代替原问题中隐式的约束和目标函数。试验设计和近似方法是近似技术的主要内容，所有的多目标优化设计的近似技术均围绕这两个方面展开。合理的试验设计是近似技术的前提，它不仅可以获得构造模型的样本点，同时可为近似方法提供充足的样本空间，而近似方法则是近似技术的主体，是确保近似精度和计算效率的核心环节。

1.1 正交试验设计

由于该微小卫星结构多目标优化设计中的因素很多，且每一因素都要选出好的试验条件，如果对这些因素采用其他试验设计方法，则需要进行的试验次数是让人难以接受的，另外，各因素的水平数相同且较小，故正交试验设计为最佳选择。

正交试验设计是一种常用的多因子试验方法，它利用正交表Ln（qp）选择试验条件和安排试验计划，并通过正交表的特点进行数据分析以合理地选择试验次数，从而确定满意的试验计划组合。其中，p、q分别表示因素的水平数和个数，下标n表示总共需要进行的试验次数。正交试验的特点是使样本点在设计范围内均匀分散，整齐可比，正交试验不仅满足让具有代表性的样本点均匀分布在试验范围内，同时提高了试验效率，方便分析各因素对指标的影响程度和变化规律。

1.2 Kriging代理模型［5－7］

从统计学的概念出发，Kriging模型是从变量相关性和变异性出发，在有限区域内对区域化变量的取值进行无偏和最优估计的一种方法。它利用对空间数据进行加权插值的权值设计方法，通过引进以距离为自变量的变异函数来计算权值，因此该模型不仅能反映变量的空间结构特性，而且能体现变量的随机分布特性。在Kriging模型中，系统的响应值与自变量之间的相互关系可表示为

其中，f（x）是一个确定性部分，称为参数项，一般用多项式或定值β表示；而z（x）则表示全局模型的局部偏差，通过样本点插值获得，主要包含以下特性：

其中，R为相关矩阵，是M×M阶对称正定对角矩阵；M为样本点个数。R（xi，xj）为任意两个样本点之间的相关函数，以广泛采用的高斯相关函数为例：

确定好相关函数后，在式（1）的基础上用β替代f（x），即可得到未知设计点响应的Kriging估计值：

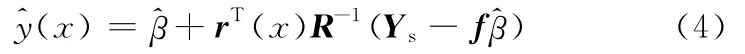
式中，Ys为样本点响应矩阵；f、rT（x）均为M维列向量。

rT（x）为观测点x与样本点（x1，x2，…，xM）T之间的相关向量：

式（3）中的相关参数θk的最大似然估计可采用下式求得：

在相关函数的作用下，Kriging模型具有局部估计的特点，使其在处理非线性程度较高的问题时较容易得到理想的拟合效果。另外，在相关函数中通过对不同参数的设定不仅能解决各向同性问题而且可以处理各向异性问题，因此Kriging模型在航空航天领域优化设计分析中具有广阔的应用前景［8］。

2 改进后的基于信赖域近似模型管理框架

如引言所述，部分学者提出的近似模型管理方法主要是通过对近似模型本身进行修正以达到较满意的求解精度。其中，Yang等［9］提出了一种序列更新Kriging近似模型的方法，安伟刚［10］提出的管理模型框架中采用了单纯形与多目标粒子群优化方法的混合算法，提高了优化效率，增强了局部搜索能力，他同时运用轮盘赌法对演化过程中的每一代选取多个个体进行高精度分析计算并根据修正点逐步对近似模型进行修正。上述两种近似模型的更新方法主要是从修正模型精度的角度出发，而刘桂萍等［11］则另辟蹊径，提出了一种基于信赖域的近似模型管理方法，通过对近似模型的搜索区域进行限制并在优化迭代的过程中对该限制区域进行更新来保证求解精度。这种近似模型管理的主要优点在于多目标优化求解过程中受近似模型精度的影响较小，主要是为了搜寻足够精确的Pareto最优解集，而并未要求构建出较高精度的近似模型。在该方法中首先将设计空间中的搜索限制域定义为初始信赖域，随后在优化过程中，从上一步迭代所得到的Pareto解集中均匀选择出一系列的解，并通过高精度分析模型对这些解进行评价，从而确定当前的近似模型与实际模型的Pareto最优解集的一致程度。最后，通过对信赖度的计算将设计变量搜索空间中的信赖域按一定的规则进行缩放和移动等更新操作，并将已评价过的且在新的信赖域范围内的样本点加入到下一代样本点中，以保证在该区域内构建的近似模型能得到与实际模型一致的Pareto最优解集。当两者的一致程度比较低时就缩小信赖域，反之则放大信赖域。因此在该方法中对于信赖度的计算尤为重要，因为信赖度的大小决定了信赖域空间的缩放程度，直接影响近似模型Pareto解集的精度。

与文献［11］提出的近似模型管理方法相比，本文提出的近似模型管理框架除了选取构建近似模型样本点的方法和优化的算法不同之外，更多的是体现在信赖度计算的准确性与合理性上。基于信赖域的近似管理模型框架的核心在于如何准确找到下一代的搜索限制域。文献［11］在进行信赖度计算时是从每一步的非支配解集中均匀选取一系列的解构成新的解集P（t）a，然后利用高精度分析模型对其评价后确定所选解集中属于高精度模型的解的集合P（t）o，根据式（9）得出两个解集中的解的个数的比值，从而确定出信赖度的大小：

通过联立式（9）～式（11）即可得出每一步迭代过程中新的搜索区域，因此信赖度值的确定直接决定了信赖域半径的缩放程度，是确定新的搜索区域的关键因素。然而，信赖度值的计算依赖于每一步迭代过程中如何从非劣解集中选取合适的解构成解集P（t）a。诚然，均匀选取的方法确实能够体现出非劣解集的整体性，但容易造成所选出的解过于接近样本点导致信赖度值较高，从而不能真实反映非劣解集对当前近似模型与实际模型的一致程度。而本文所采用的方法如下：首先计算从上一步得到的Pareto解集中的每个解到所有样本点的距离，以最小的距离作为该解到样本集的距离；然后从中选择距离最大的N个解构成解集P（t）a。由于构建近似模型采用的样本点即为初始样本点，而通过该方法选出的解均与最初的样本点保持一定的“距离”，因此信赖度的计算结果具备较高的可信度，对信赖域的缩放也更为合理。该近似模型管理框架的整体流程如图1所示。

图1 近似模型管理框架流程图

3 微小卫星主承力结构多目标优化设计

3.1 优化数学模型的建立

通过计算得到某型号微小卫星整星在X、Y、Z三个方向的一阶频率f1、f2、f3分别为34.59Hz、37.23Hz和94.65Hz，主承力结构总质量为17.162kg。考虑各阶模态所占比重不同，将整星的前三阶模态作为一个整体，并对各阶模态赋予相应的权重组成一个目标函数。同时，微小卫星结构轻量化设计是目前小型卫星结构设计技术的发展趋势，因此将整星的加权频率和结构总质量作为优化设计的目标函数，即

式中，α1、α2、α3为整星X、Y、Z方向一阶频率所对应的权重系数；m为整星主承力结构总质量。

优化问题通常是求解目标函数的最小值，因此引入一个定值Q，构造一个关于整星频率的减函数，从而使得在满足目标函数取得最小值的同时α1f21＋α2f22＋α3f23取得最大值。由于该微小卫星的主承力结构（图2）除了6根铝质骨架外其余均为铝蒙皮蜂窝夹层板，故重点考虑主承力结构上的各块蜂窝板对整星刚度和结构质量的影响。选取主结构中的骨架厚度、所有蜂窝板的铝面板厚度和蜂窝芯的高度为设计变量，如图2、图3所示。直接约束条件为：铝面板厚度介于0.1～0.8mm 之 间， 蜂 窝 芯 子 高 度 介 于10～80mm之间。间接约束条件一般分为刚度条件和强度条件，主要包括优化后的整星前三阶频率较原始频率有相应提高，且结构应力要小于规定的许用应力。

图2 整星主承力结构图

图3 铝蒙皮蜂窝夹层结构图

根据上述描述可以建立如下数学优化模型：

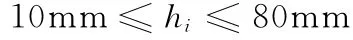
式中，σmax为整星最大输出应力；［σ］为许用应力；d为骨架厚度；t1、t2、t3、t4、t5分别为底板、中层板、顶板、侧板、隔板的面板厚度；h1、h2、h3、h4、h5分别为底板、中 层板、顶板、侧板、隔板的蜂窝夹心层厚度。

Q为一定值，取值为500Hz；各阶频率的权重系数α1、α2、α3根据其重要程度分别取0.6、0.3和0.1。

3.2 近似模型的建立

根据该微小卫星结构多目标优化的特点，采用上述近似模型管理框架中的正交试验和Kriging近似方法用于构建近似模型。其中因素个数为11，均设定为5个水平，表示如下：

为了确定样本点的分布，本文选用L50（511）进行表头设计。通过正交试验和PATRAN／NASTRAN有限元分析软件计算得到了50个样本点及其所对应的响应值。由于参数项f（x）的选取对于模型精度的影响较小，为了简化建模过程，采用线性回归模型，设定回归量为常数1。相关函数的核函数是决定模型精度的核心，因此采用计算效果最好的高斯函数（式（3））。通过上述函数和参数的设定，最优的Kriging模型的构建问题被转换成一个非线性的无约束优化问题，从而通过对相关参数θk的搜索即可建立一个无偏的Kriging模型。

3.3 优化结果

图4 微小卫星结构多目标优化非劣解前沿曲线

选取基于拥挤距离的多目标粒子群算法作为优化的核心算法，其中的参数选取为：种群规模200，最大迭代数100。图4所示为样本点计算次数为50时得到的Pareto最优解集在目标空间中的象点，其中点A和B为边界点。采用该近似模型管理框架得到了较为满意的优化结果，非劣解前沿曲线分布较均匀。同时，近似技术的运用大幅度提升了优化效率，有限元仿真分析的计算次数为3400，耗时29 485.52s。由于设计变量较多，优化过程中的计算时间主要耗费在样本点的有限元数值模拟计算中。优化结果表明，该方法能够在较短的时间内得到多个可供选择的Pareto最优解，具有较高的求解效率和求解精度，同时不仅保证了解集未开裂而且得到的起皱区域较小。根据不同偏好从以上的非劣解前沿曲线中选择了五组解作为最优妥协解，目标函数及设计变量的结果如表1所示。

表1 五组非劣解的优化结果

从表1可以看出，优化后各方案中整星在X、Y、Z三个方向上的一阶频率均有不同程度的提高，特别是方案3和方案5的整星基频超出原设计方案20%以上，同时整星结构质量也有一定程度的减小。另外，值得注意的是，各设计变量随目标函数值的变化趋势基本一致，均保持在同一数量级范围内。各方案除底板蜂窝夹层厚度较原设计方案略有增大之外，隔板、中层板、顶板和侧板均有不同程度的减小，特别是6块侧板的蜂窝夹层厚度在优化后减小了约50%。由于整星刚度提高，底板作为主承力板其面板厚度有较大幅度增大，5组方案的优化结果均在0.43～0.54mm之间，较之前提高了42%左右。总体而言，各方案的优化效果均较为明显，达到了优化的目的。

4 结语

由于基于信赖域的近似模型管理方法对构建近似模型精度的要求不高，因此要保证在可能的非支配解区域内近似模型与高精度模型的非支配解集的一致性必须重点控制对信赖域的更新。本文通过采用最大最小距离策略从每一步迭代过程中得到的Pareto解集中选取距离最大的若干个解用于高精度分析模型的评价，保证了计算信赖度的准确性以及信赖域缩放的合理性，最终确保了在搜索区域内近似模型与高精度模型具有一致的非支配解集。该近似模型管理框架在微小卫星主承力结构多目标优化设计中的成功应用验证了它解决多因素的复杂多目标优化问题的较高工程应用价值。

［1］Coello C，Pulido G T，Lechuga M S.Handling Multiple Objectives with Particle Swarm Optimization［J］.Evolutionary Computation，2004，8（3）：256－279.

［2］Hu X H，Eberhart R.Multiobjective Optimization Using Dynamic Neighborhood Particle Swarm Optimization［C］／／IEEE World Congress on Computational Intelligence.Honolulu.HI，2002：1677－1681.

［3］于广滨.航空用微小型减速装置多目标优化设计及性能分析［D］.哈尔滨：哈尔滨工业大学，2009.

［4］安治国，周杰，赵军，等.基于径向基函数响应面法的板料成形仿真研究［J］.系统仿真学报，2009，21（6）：1557－1561.

［5］Jack P C.Kriging Metamodeling in Simulation：a Review［J］.European Journal of Operational Research，2009，192（3）：707－716.

［6］徐亚栋，钱林方，陈龙淼.基于Kriging方法的复合材料身管结构近似分析［J］.中国机械工程，2007，18（8）：988－990.

［7］任庆祝，宋文萍.基于Kriging模型的翼型多目标气动优化设计研究［J］.航空计算技术，2009，39（3）：77－81.

［8］韩永志.涡轮叶片多学科设计优化及近似技术研究［D］.西安：西北工业大学，2007.

［9］Yang B S，Yeun Y S，Ruy W S.Managing Approximation Models in Multiobjective Optimization［J］.Structural and Multidisciplinary Optimization，2002，24（2）：141－155.

［10］安伟刚.多目标优化方法研究及其工程应用［D］.西安：西北工业大学，2005.

［11］刘桂萍，韩旭，官凤娇.基于信赖域近似模型管理的多目标优化方法及其应用［J］.中国机械工程，2008，19（10）：1140－1143.