非接触机械密封的非线性动特性系数及瞬态振动响应分析

王技德 张国渊

1.兰州职业技术学院，兰州，730070 2.西北工业大学，西安，710072

0 引言

非接触密封作为重要装备的关键基础件，被广泛应用在航空航天、能源环境、石油化工等领域（如石化泵、涡轮泵及核泵等）中［1－4］。在一些极端工况条件下，由于轴向振动过大或者受到瞬态冲击，机械密封经常会出现变形或者密封副表面损坏等，这些现象极易引起密封的失效［2，5－6］。考虑瞬态过程非线性因素的振动特性研究正成为非接触式机械密封设计和研究中的一个重要内容［3］，这对机械密封可靠、稳定地运行有着举足轻重的作用，因此对机械密封瞬态快速启动过程的响应特性进行研究就变得更为重要。然而已有的研究大多是采用商用软件对密封模型进行流固耦合下的稳态性能分析，主要是对其静态润滑特性进行分析，如研究密封的膜厚变化、平均温升、热变形等，对振动响应研究较少。张国渊等［1，2，7］对非接触机械密封瞬态启动过程中脱开转速和密封可控性进行了研究，分析了密封的静态润滑特性和密封效应；Brunetière等［4，8］研究了密封的稳态热动力模型及稳态热效应；王之栎等［5］、张伟政等［9］研究了气膜密封因外界扰动而引起的振动和角向摆动对密封动态特性的影响；贺立峰等［6］分析了弹簧刚度改变对端面接触式机械密封振动的影响；丁雪兴等［10］对螺旋槽干气密封系统非线性动力学行为进行了研究。然而，上述研究都未对密封考虑摆动时的非线性相关的动态特性系数进行研究，对其瞬态过程的振动特性的研究也很少。为此，本文提出考虑倾斜情况的弹性补偿单元支撑的包含Reynolds方程、运动方程等的非接触机械密封瞬态非线性振动分析模型，并以此研究受外部轴向冲击载荷时密封的振动响应以及响应过程中密封的非线性轴向力、刚度和阻尼系数的响应特征。

1 瞬态非线性振动响应模型

1.1 瞬态Reynolds方程

本文研究的非接触机械密封结构见图1，它依靠在密封端面间形成的微小间隙（流体膜）实现密封副的非接触密封，其密封机理是，允许微小的在可控制范围内的流体泄漏，但保证密封的长寿命、高可靠性以及密封良好的外部轴向小振动的跟随性。

图1 非接触机械密封示意图

根据流体力学中的N－S方程和连续性方程，在相应的假设条件下可得到柱坐标（r，θ）下的量纲一 Reynolds方程［11］：

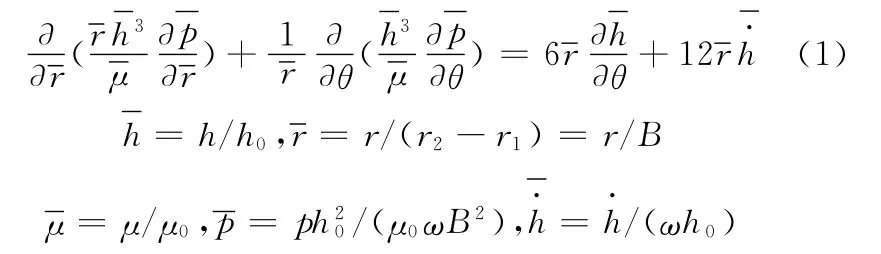
式中，r1、r2、B 分别为密封环外径、内径和径向长度；h、h0分别为瞬态、稳态时油膜厚度；μ0为初始动力黏度；ω为转速 ；p 为 油 膜 压 力 值 ，h·为油膜的挤压速度。

量纲一边界条件为

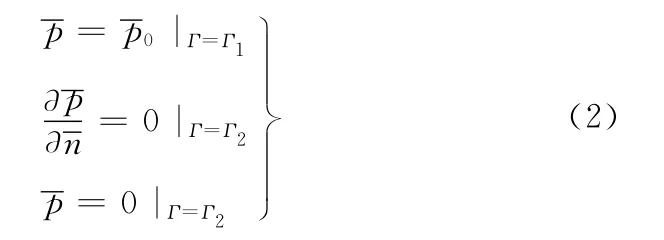
其中，p0为边界压力值；n为法线方向；Γ1表示密封的介质入口，Γ2表示除Γ1外的其他边界，Γ表示全部边界。

1.2 瞬态运动方程

根据Newton力学第二定律，可以建立动环和静环配对的动力学方程和静环力矩平衡方程如下：

式中，z为密封环轴向运动量；m为密封环的质量；Kz、Kz·分别为油膜对密封环的力刚度与阻尼系数；F（t）为外部轴向载荷变化量（稳态时，F（t）＝0）；J为密封环的转动惯量；Kφ、Kφ·分别为油膜对密封环的力矩刚度和阻尼系数；φ为倾斜静环的倾角；N（t）为油膜对密封环的外力矩（倾覆力矩）。

从式（3）、式（4）可以看出，密封环的轴向运动与其倾斜摆动无关。实际上并非如此，密封副振动影响油膜厚度分布，从而使油膜压力分布发生变化，结果导致产生倾覆力矩而使得密封环摆动。同样，密封环摆动也会引起轴向振动，这可以从下面的分析看到，然而线性分析是无法了解密封环运动与摆动之间的关系的。

1.3 考虑密封环倾斜的密封间隙方程和轴向载荷

密封间隙控制方程为

式中，hp为弹性补偿单元作用支点处的油膜厚度；θp为密封倾斜节线的周向角。

对密封间隙内油膜承载区域的压力进行积分，可得到油膜轴向承载力公式：

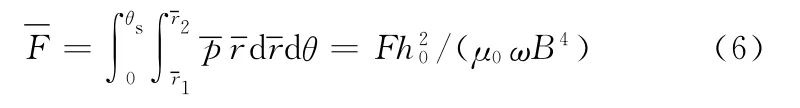
式中，F为承载力；θs为油膜边界值。

非接触机械密封正常工作过程中，由油膜产生的轴向承载力即为密封开启力，密封的闭合力由弹簧等补偿单元的弹性补偿力和密封腔内作用在密封环的介质压力构成，这些力构成的闭合力和开启力的大小相等、方向相反。

对于考虑密封环倾斜的机械密封，还必须考虑其倾覆力矩：

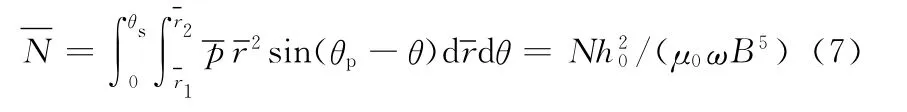
1.4 二阶非线性动特性求解模型

1.4.1 密封间隙的油膜厚度二阶级数

油膜厚度在扰动下的方程为

式中，φ0为稳态下的密封静环倾角；Δz为h0沿轴向的增量；Δφ为φ0沿周向的增量。

在瞬态下有

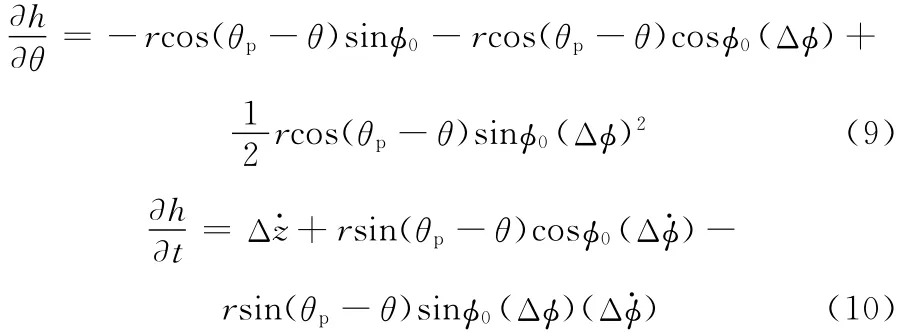
1.4.2 密封开启力及倾覆力矩的二阶级数

静态开启力为F0时，瞬态下密封间隙内油膜对密封副的作用力矩阵形式为

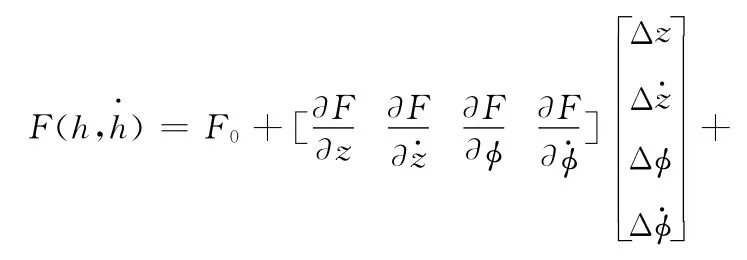
瞬态下油膜对倾覆力矩的矩阵形式为

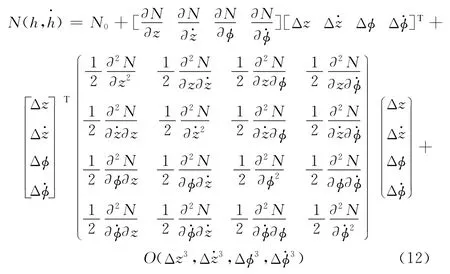
1.4.3 二阶非线性动特性系数

静态倾覆力矩为N0时，瞬态下油膜对密封的开启力用刚度阻尼系数的矩阵形式表示为

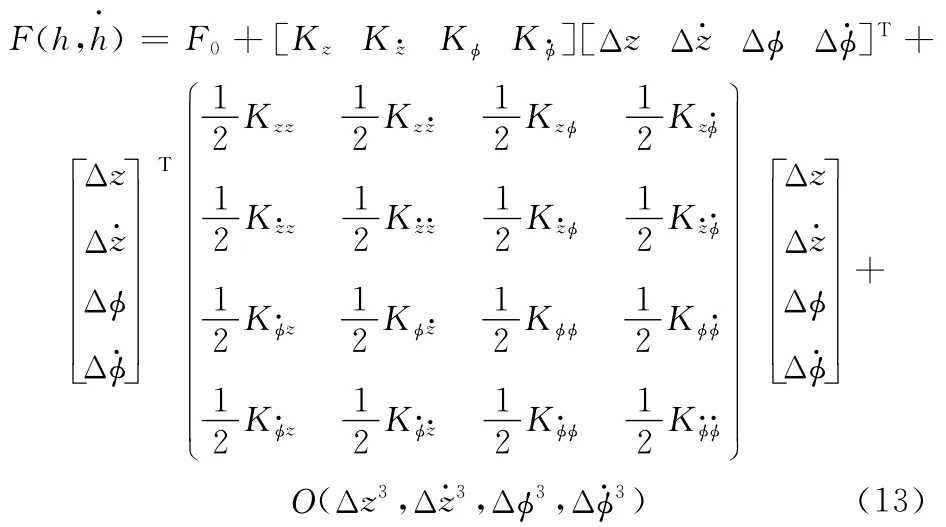
其中，K 为力刚度阻尼参数，下标z、φ、z·、φ·分别表示沿轴向、周向的位移和速度项。

由式（6）、式（11）、式（13）可得到瞬态下油膜对密封环的作用力的非线性动力学系数，其中线性刚度系数为（P为量纲一压力）

线性阻尼系数为

二阶非线性主刚度和交叉刚度系数为

二阶非线性主阻尼和交叉阻尼系数为

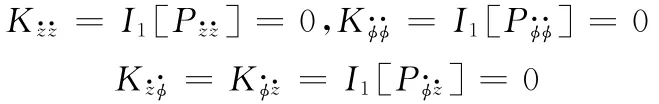
非线性刚度阻尼耦合系数为

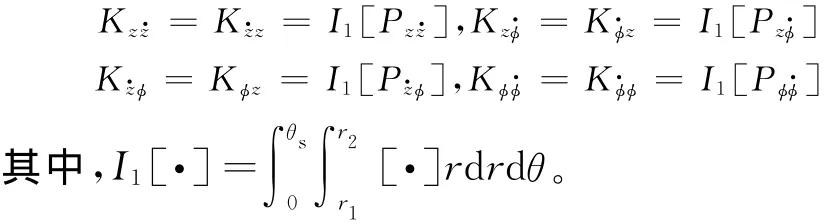
瞬态下油膜引起的倾覆力矩用摆动刚度阻尼系数表示的矩阵形式为（V为摆动刚度阻尼系数的统一标示量）：

由式（7）、式（12）、式（14）可得到油膜对倾覆力矩的线性及非线性动力学系数，其中线性刚度系数为

线性阻尼系数为

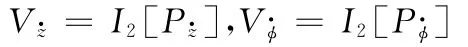
二阶非线性刚度系数为

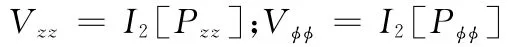
二阶非线性交叉刚度系数为

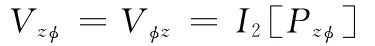
二阶非线性阻尼系数为

二阶非线性交叉阻尼系数为

二阶非线性刚度阻尼耦合系数为

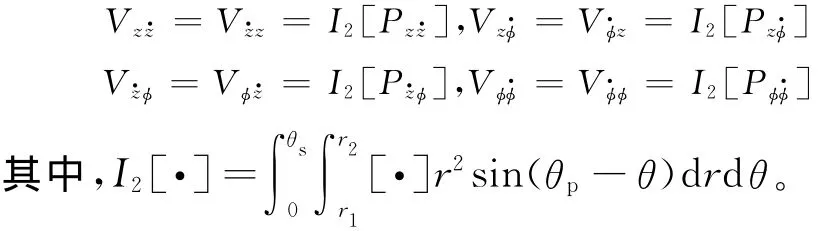
由式（13）和式（14）知，瞬态油膜作用时，与密封副轴向力和倾覆力矩相关的动特性系数各有20个，由于式（13）和式（14）中矩阵是对称的，因此分别包含14个动特性系数。

从推导中知：

（1）非线性阻尼系数均等于0，这说明油膜阻尼对密封副和摆动的影响是线性的，这是由于瞬态Reynolds方程中瞬态项∂h／∂t是一阶的缘故。

（2）密封副振动影响油膜厚度分布，从而使油膜压力分布发生变化，导致密封环摆动；同样，密封副摆动也会引起密封轴向振动。

1.4.4 瞬态运动方程

考虑密封环的惯性时，将刚度阻尼代入式（5）和式（6）后，密封环的二阶非线性量纲一轴向振动方程为

摆动下的二阶非线性量纲一运动方程为

2 算例分析

2.1 计算对象和刚度阻尼计算结果分析

计算对象机械密封的几何参数如下：r1＝0.125m，r2＝0.21m，θs＝0.452rad，θp＝0.265rad；被密封介质温度t＝40℃，μ0＝0.04315Pa·s，密度998kg／m3。密封运行条件：ω＝3500r／min，轴向载荷W ＝1.8×105N。

在已有程序基础上［1，7，12］，引入式（8）～ 式（14），编制程序并计算，获得的非线性动特性系数的量纲一数值如表1所示。

表1 动特性系数的量纲一数值

2.2 密封瞬态振动响应过程计算结果分析

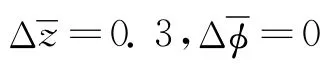
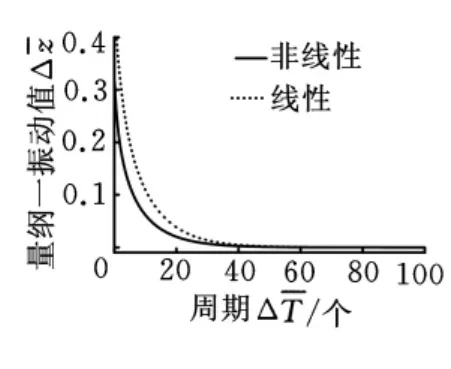
图2 轴向振动响应（＝0.3，＝0）

图3 摆动响应（＝0.3，＝0）

图4 轴向振动响应（＝0，＝1.0×10－3）

图5 摆动响应（＝0，＝1.0×10－3）

3 结论

（1）建立了考虑倾斜情况的弹性补偿单元支撑的非接触机械密封瞬态振动响应分析模型，该模型包括了瞬态Reynolds方程、运动方程以及二阶非线性动特性求解方程等。（2）通过Euler法求解获得了非接触机械密封在轴向振动位移和静环倾角随时间变化时的瞬态振动响应特性。（3）计算得到了瞬态油膜对密封副作用力和倾覆力矩的各14个动特性系数，结果表明：油膜阻尼对密封副和摆动的影响是线性的；密封的副振动影响油膜厚度分布，从而引起油膜压力分布发生变化，导致密封环摆动；密封副摆动同样也会引起密封轴向振动。

［1］Zhang G Y，Zhao W G，Yan X T，et al.Theoretical and Experimental Study on Characteristics of Water－lubricated Double Spiral Grooved Seals［J］.Tribology Transactions，2011，54（3）：362－369.

［2］张国渊，赵伟刚，闫秀天，等.可控式液体润滑高速螺旋槽端面密封试验研究［J］.航空动力学报，2010，26（4）：947－953.

［3］彭旭东，王玉明，黄兴，等.密封技术的现状与发展趋势［J］.液压气动与密封，2009（4）：4－11.

［4］Brunetière N，Galenne E，Tournerie B，et al.Modelling of Non－laminar Phenomena in High Reliability Hydrostatic Seals Operating in Extreme Conditions［J］.Tribology International，2008，41（4）：211－220.

［5］王之栎，刘国西，郭艳丽.反转轴间气膜密封振动过程分析［J］.振动与冲击，2011，30（2）：181－185.

［6］贺立峰，朱汉华，范世东，等.弹簧刚度对端面接触式机械密封振动的影响［J］.润滑与密封，2010，36（6）：64－68.

［7］张国渊，袁小阳，赵伟刚，等.螺旋槽端面密封脱开转速的理论及实验研究［J］.机械工程学报，2008，44（8）：55－60.

［8］Brunetière N，Apostolescu A.A Simple Approach to the ThermoElastoHydroDynamic Behavior of Mechanical Face Seals［J］.Tribology Transactions，2009，52（2）：243－255.

［9］张伟政，俞树荣，丁雪兴，等.干气密封系统角向摆动的稳定性及其振动响应［J］.振动与冲击，2011，30（3）：96－99.

［10］丁雪兴，张伟政，俞树荣，等.螺旋槽干气密封系统非线性动力学行为分析［J］.中国机械工程，2010，21（9）：1083－1087.

［11］平克斯·O，斯德因李希特·B.流体动力润滑理论［M］.西安交通大学轴承研究小组，译.北京：机械工业出版社，1980.

［12］李治国，张国渊，袁小阳，等.流体动静压端面密封的静动特性分析［J］.中国机械工程，2006，17（5）：457－460.