钢管端面铣头倒棱机夹紧机构的优化设计

芮成杰，柴晓艳

(1.天津理工大学天津市复杂系统控制理论及应用重点实验室，天津 300384;2.天津理工大学机械工程学院，天津 300384)

1 概述

钢管在国民经济中占有重要的位置，其用量以每年几百万吨的速度增长。为了生产高质量、高附加值的钢管，扩展钢管更广泛的用途，需对钢管端面铣头倒棱去毛刺。为了保证高精度的加工钢管，钢管端面铣头倒棱机的夹紧机构必须保证钢管在加工的过程中不发生前后位移、振动及旋转。本文运用ADAMS软件，利用参数化表达式、参数点坐标、运动参数化、使用设计变量等手段进行参数化建模，分析夹紧机构各杆件的位置关系，计算所需的夹紧力，对夹紧机构进行优化设计，满足钢管加工过程中的夹紧要求。

2 夹紧机构的工作过程

φ114全自动钢管端面铣头倒棱机的夹紧机构是一个多杆机构，采用气缸驱动。该机构的工作目的是将送到夹紧机构的钢管夹紧，保证钢管在加工的时候不发生前后位移、振动和周向旋转，保证钢管能够被精确的加工。

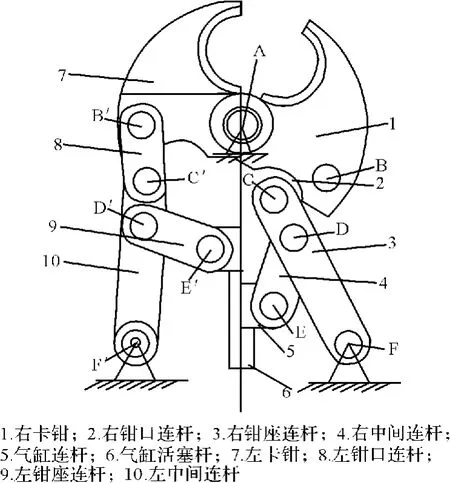
图1 夹紧机构简图Fig.1 Diagram of clamping mechanism

图1为夹紧机构简图，为了说明工作过程，图1给出了两种状态，左面为钳口夹紧状态，右边是该机构钳口敞开最大的状态。工作时左右是完全对称的。工作时活塞杆6伸出，带动气缸连杆5向前推进，连杆5带动中间连杆4绕铰链转动;同时，杆4通过铰链D推动右钳座连杆3绕铰链F转动，使得3杆带动右钳口连杆2绕铰链C转动，杆2通过铰链B推动右卡钳1绕连接在机架上的铰链A转动，这些转动完成后，既为左边机构的状态，进而通过左右卡钳夹紧焊管。夹紧后倒棱机开始对钢管进行铣头、倒棱等工作。当钢管加工完成后，活塞杆6收回，通过各连杆，带动左右卡钳张开，卸下钢管。

3 夹紧机构的优化设计

3.1 优化目标

建立夹紧机构模型，如图2所示。进行运动学仿真，观察气缸活塞杆5处所给出的运动推力的变化情况。气缸活塞杆5是原动件，推进时匀速向上运动。力的变化曲线如图3所示。该机构的优化目标是改变各杆件的位置参数，使机构在夹紧的过程中，推进力最小。

图2 夹紧机构模型Fig.2 Model of clamping mechanism

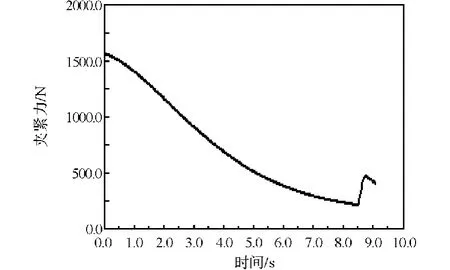
图3 优化前推进力变化曲线Fig.3 Curve of propulsive force before optimization

3.2 参数化建模

由于机构为对称结构，选取机构的右半部分作为研究对象。如图4所示，虚线为夹紧位置，右半部分创建了5个参数化点，18个主要设计变量。图4中未显示的设计变量除了L3外均为设计过程中产生的变量。

3.2.1 P1点

点P1(X1，Y1)转过一个定值θ角后到达点P'1(X1'，Y'1);图4中ρ为杆件L1与直线Y=YA的夹角，P1点的参数变化范围始终在Y=YA的下方，夹紧后到达P'1点位置，此时在Y=YA的上方)，则

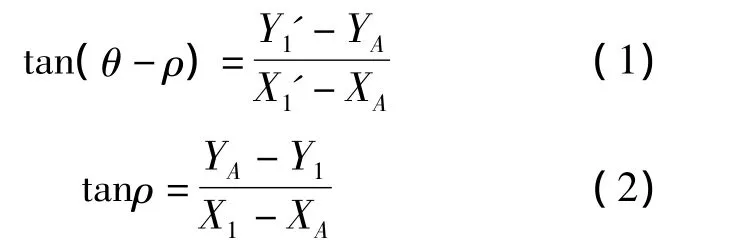
将式 (2)带入式 (1)得

因P1和均在以A点为圆心，L1为半径的圆上，则

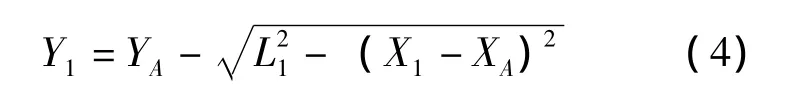
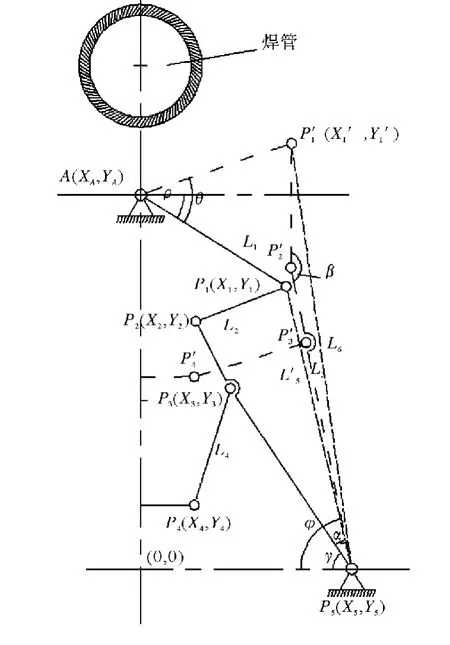
图4 夹紧机构参数关系几何图形Fig.4 Geometric figure for parameter relationship of clamping mechanism

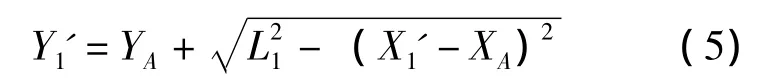
把式 (4)、式 (5)带入式 (3)，求出X1'的表达式为

式中，XA=0;YA=349;L1=160;θ=32.2°。

在ADAMS中的参数表达式中，只有X1一个自变量，Y1、Y'1为因变量。

3.2.2 分析点P2和P5

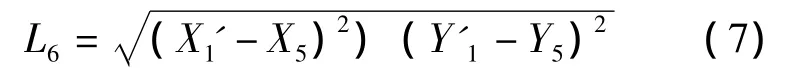
把式 (5)带入式 (7)，则

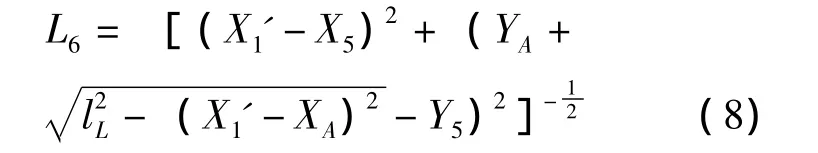
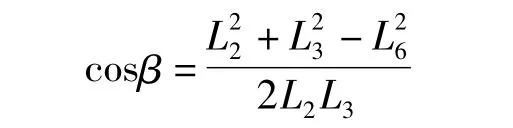
即

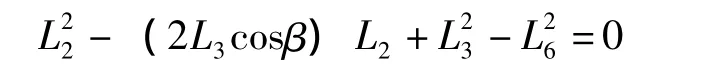
把L3当成自变量，用L3把L2表示出来，由一元二次方程求根公式求得

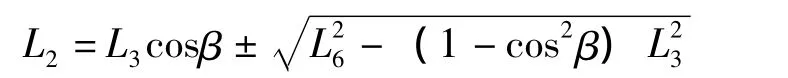
由于L2＞0，故取

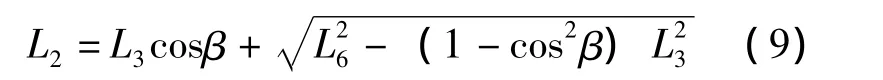
把P1P5设置为L5，则由图4可知

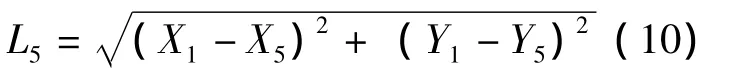
在图4中，γ=φ－α，有

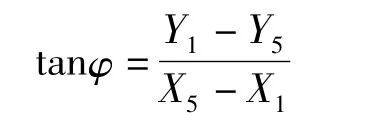
即

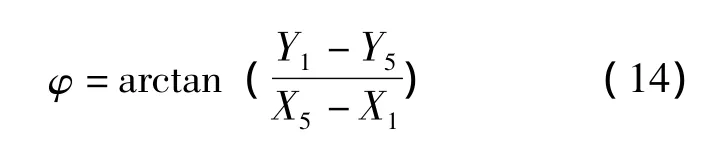
在图 4三角形△P1P2P5中，P1P2=L2，P1P5=L5，P2P5=L3由余弦公式可得

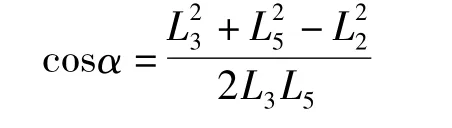
即

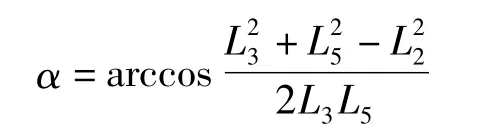
由于γ=φ－α，根据式 (11)和式 (12)可得

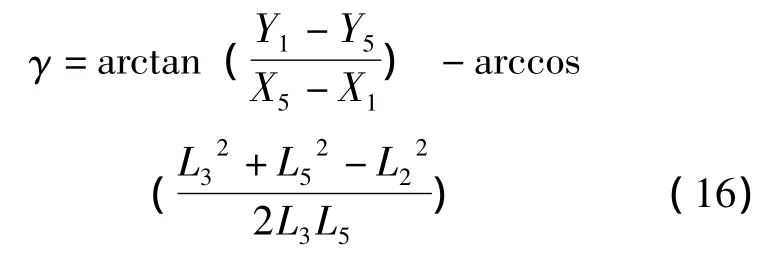
由图4得出P2点的坐标表达式为

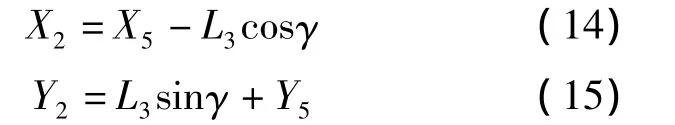
在ADAMS中的表达式中X5、Y5、L3为自变量，其余为因变量。

3.2.3 分析点P3和点P4

由图4可知，

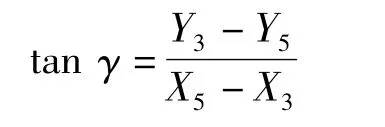
则

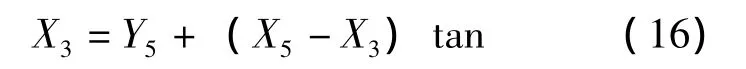
式中，将X3设置为自变量。

在图5中，把 AP5设置为 LA5，LA5为因变量，则

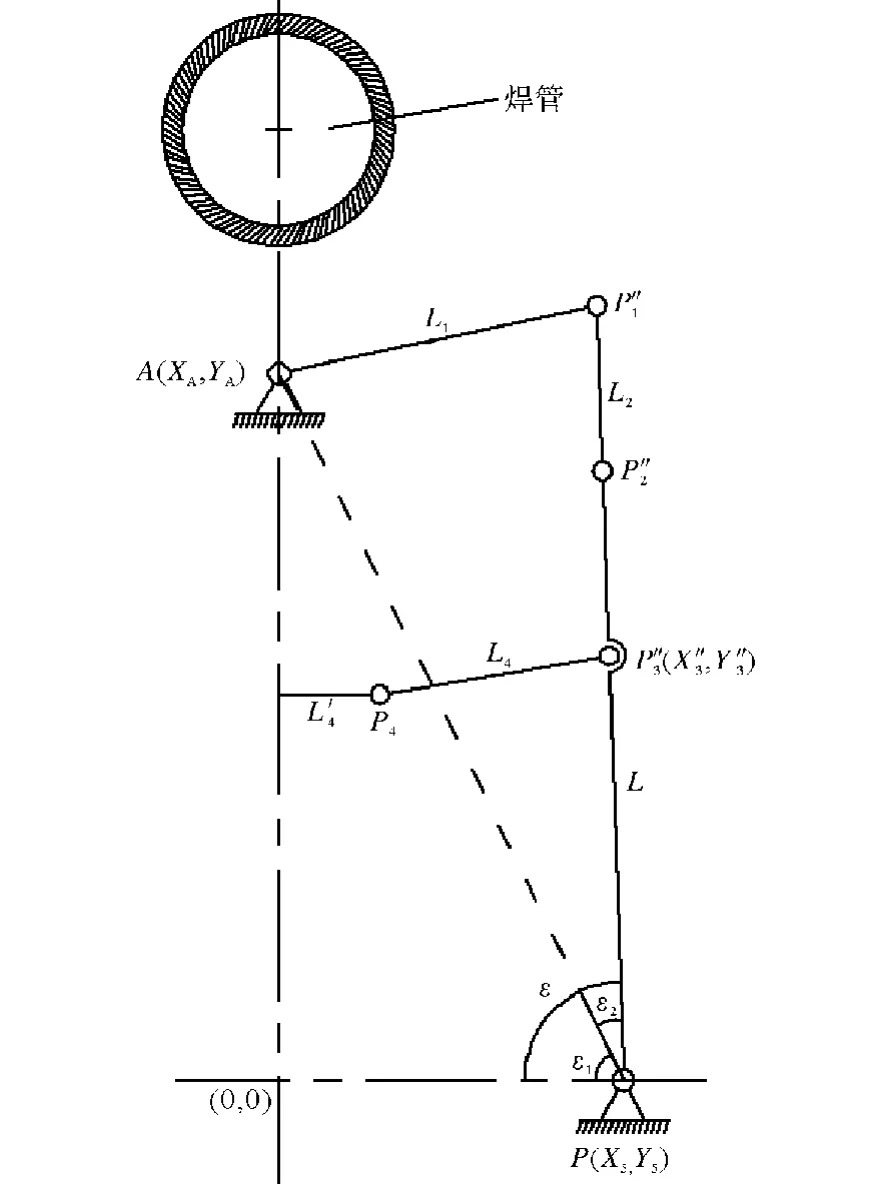
图5 机构极限运动位置Fig.5 Limited moving position of clamping mechanism

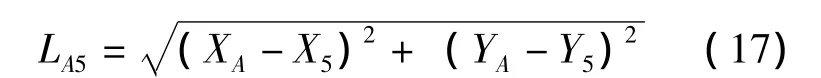
如图5所示，机构必须能够运动到点P″1、P″2、P″3、P5在同一条直线的位置，则在△AP5P″1中，由余弦函数可知:

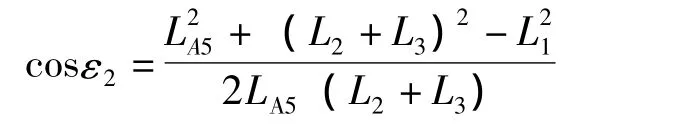
则

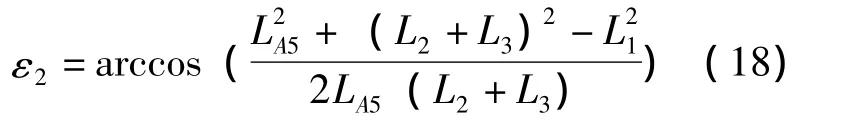
在图5中，有

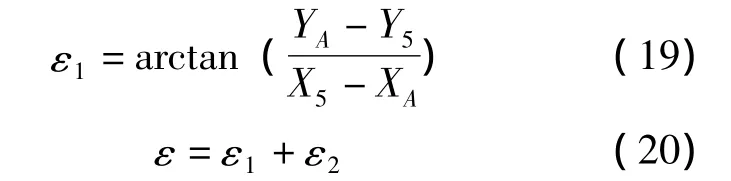
将式 (17)、 (18)和 (19)代入式 (20)可得

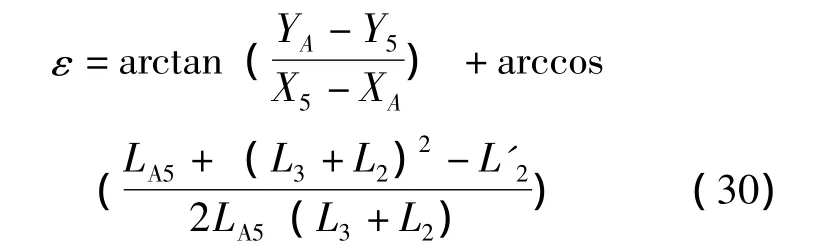
在图5中必须满足如下关系

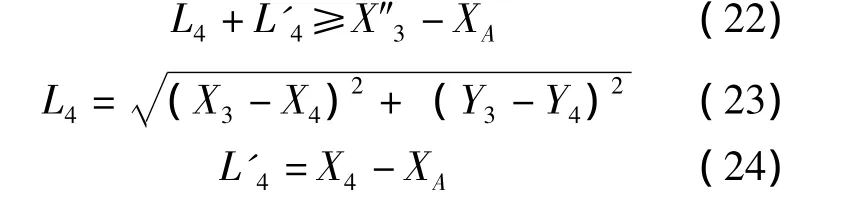
设点P3距点P5的距离为L，由图4可知

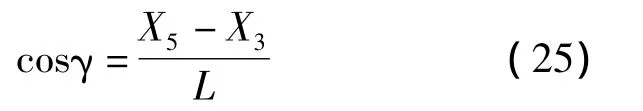
由图5可知

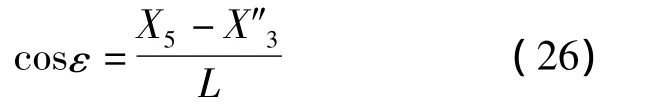
将式 (25)和式 (26)相除消去L，解出X″3可得如下关系式:

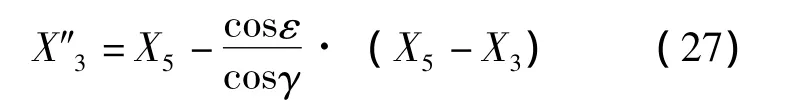
把式 (23)、式 (24)和式 (27)代入式(22)，整理可得

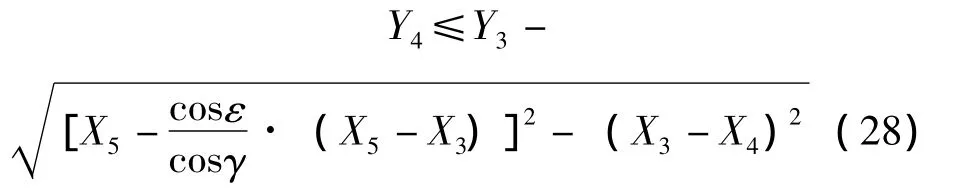
式 (28)中取等号。

则在ADAMS中各参数表达式中，X3和X4是自变量，其余为因变量。

至此，完成了夹紧机构的建模。左半部分也设置了对称的五个参数点，这五个点与右半部分的五个参数点完全对称，这里不再一一叙述。

在仿真分析中，当夹紧机构转过图4所示的角后，钢管被加紧，系统停止仿真，为此，建立了传感器，以测量夹紧机构的角度变化，当转过角时，仿真运动立即停止。

3.3 优化设计

ADAMS/view的参数化分析功能可以分析设计参数变化对样机性能的影响。在参数化分析过程中，，ADAMS/view采用不同的设计参数值自动地进行一些列仿真分析，然后返回分析结果。通过对参数化分析结果的分析，可以研究一个或多个参数变化对样机性能的影响，获得最优的样机。

3.3.1 确定优化参数

由以上分析可知，设计变量 X1、X5、Y5、L3、X3、X4为自变量。对其进行灵敏度分析，结果见表1。

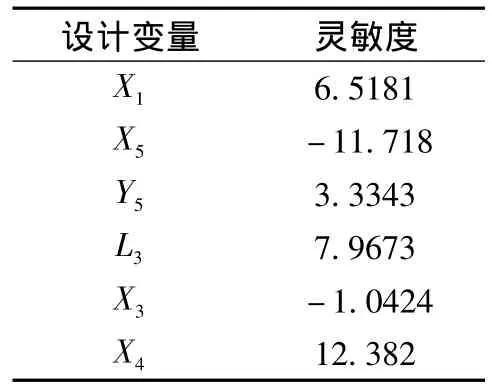
表1 设计变量灵敏度分析Tab.1 Sensitivity analysis of design variables

对以上变量分析可知，X1、X5、L3、X4灵敏度较高，对机构影响较大，其中X5是与机构整体尺寸有关的参数。对参数进行两种优化:第1种，改变整体尺寸，把四个变量X1、X5、L3、X1作为自变量进行优化;第2种，不改变整体尺寸，即舍弃X5，把X1、L3、X4作为自变量进行优化。

3.3.2 确定优化范围

两种优化方案中总共涉及四个变量，其变化范围分析如下:X1为P1点的X坐标，P1点必须在卡钳上，X最大取值为 =160，最小取值为初始位置，所以 X1的变化范围为 (135.387，160);X5为P5点的X坐标，P5点为夹紧机构与箱体连接的位置，变化不宜过大，其变化范围为 (150，190);L3为连杆的长度，长度的改变会影响铰链C和铰链D的位置关系，极限位置为铰链C与铰链D重合，所以L3的变化范围为(87，286);X1为P4点的X坐标，其变化范围为 (0，X5)。

3.3.3 优化计算和分析

两种优化方案遵循相同的步骤:在完成了参数化分析的准备工作以后，便可以做优化计算;在Build菜单下，选择测量Y方向上力的变化，在Simulate→Design Evalution→Measure下选择测量最大值，在优化目标下选择最小值。优化的时候，必须保证Y3＜Y2，优化的时候加一个约束OPT_CONSTRAINT加以控制，即 (Y3－Y2)。优化后，分析两种优化方案的结果。

第1种优化方案，改变机构的整体尺寸，对X1、X5、L3、X4优化后，迭代过程中最大推进力的变化曲线如图6所示;推进力的变化曲线如图7所示。

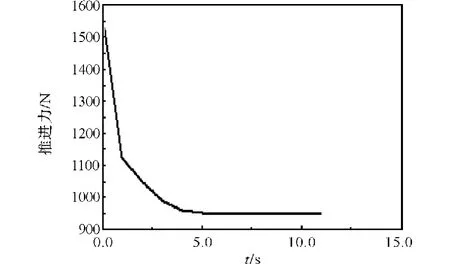
图6 迭代过程中最大力变化曲线Fig.6 Variation of maximum propulsive force in iterative process

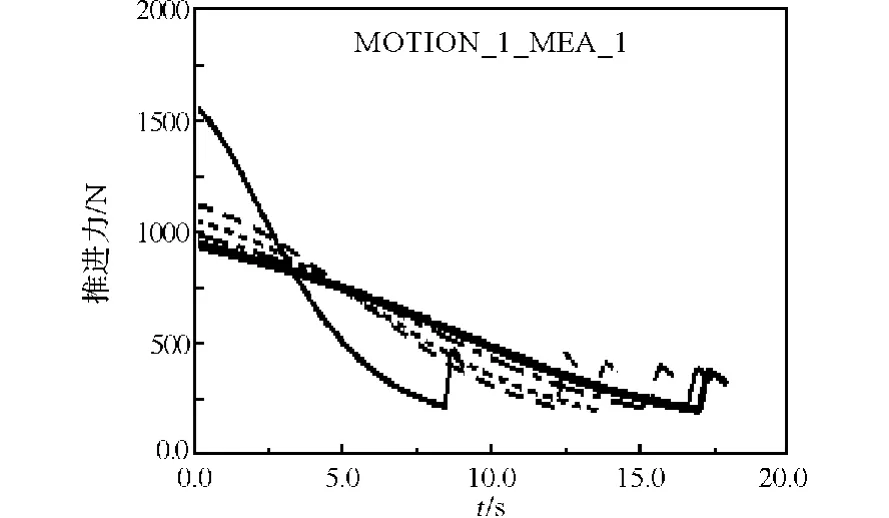
图7 迭代过程中力的变化曲线Fig.7 Variation of propulsive force in iterative process

从设计研究报告可以得到优化后各个变量的取值及气缸活塞杆所出最大力值见表2。从表2可以看出，X1、X5、L3、X4都有所变化，其中X5的变化使得机构整体尺寸发生变化，X4=0，使得气缸连杆长度变为零。优化后，最大推进力降低了39.6%，平均推进力降低了23.6%。优化后总功耗为

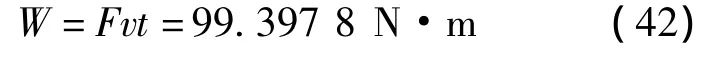
式中，F为推进过程中力的平均值，F=552.9782N;v为推进速度，v=0.01 m/s;t为推进时间，t=17.975 s。

表2 夹紧机构第1种优化结果Tab.2 The first optimization results of clamping mechanism

第2种优化方案，在不改变机构整体尺寸的前提下优化。此时，舍弃变量 X5，对 X1、L3、X4进行优化。迭代过程中最大推进力的变化曲线如图8;推进力的变化曲线如图9所示。

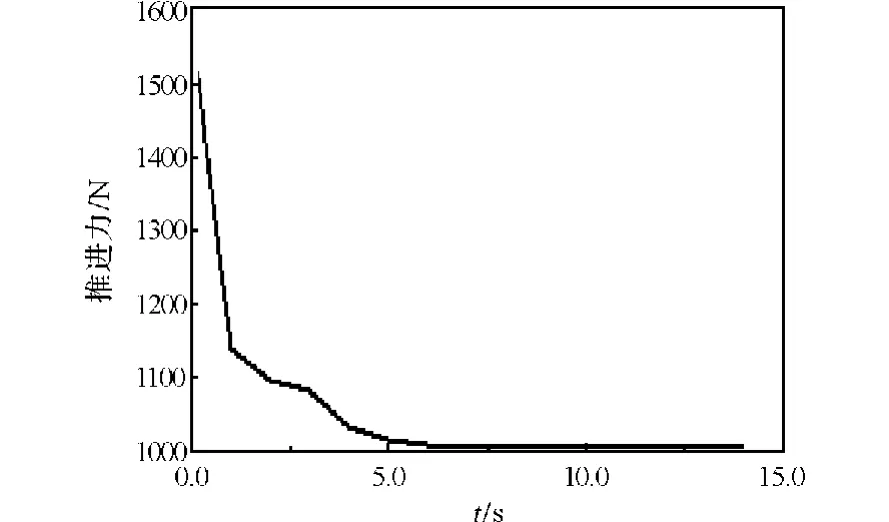
图8 迭代过程中最大力变化曲线Fig.8 Variation of maximum propulsive force in iterative process

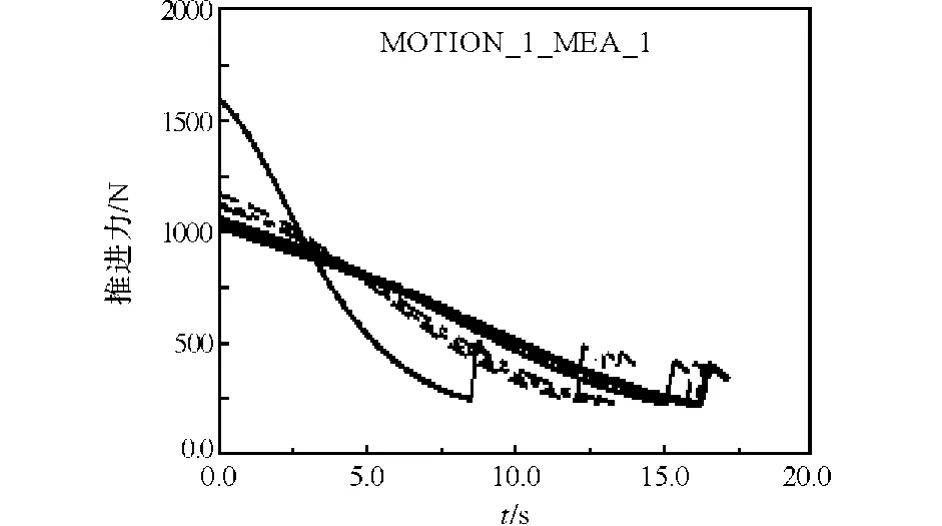
图9 迭代过程中力的变化曲线Fig.9 Variation of propulsive force in iterative process

从设计研究报告可以得到优化后各个变量的取值及气缸活塞杆所出最大力值见表3。从表3可以看出，各个变量都有所变化，其中X4=0，即气缸连杆长度仍为零，优化后，最大推进力降低了36.0%，平均推进力降低了20.1%。优化后总功耗为

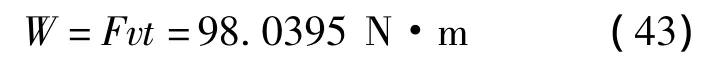
式中，F=552.9782 N;v=0.01 m/s;t=17.10 s。

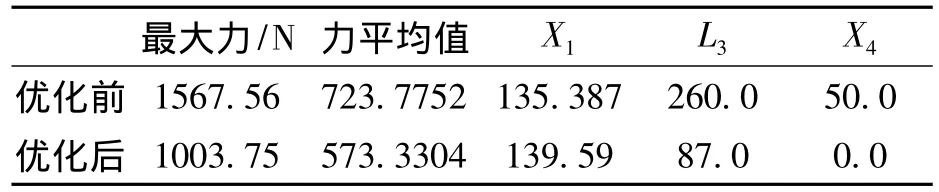
表3 夹紧机构第二种优化结果Tab.3 The second optimization results of clamping mechanism

综合比较上述两种优化方式见表4所示。

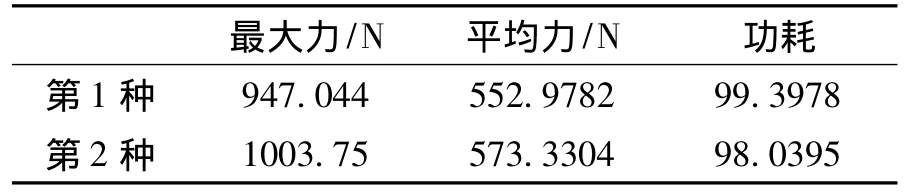
表4 两种优化方式结果对比Tab.4 Contrast of two optimization ways

从表4可以看出，两种优化结果差别不是很大，功耗基本相同，但第一种夹紧机构整体尺寸在X方向 (横向)增加了10%，为了节省成本，不改变夹紧机构整体尺寸，故选用第二种优化方案。

4 结论

本文利用ADAMS软件建立了全自动钢管端面铣头倒棱机夹紧机构的仿真分析模型，并进行了改变机构整体尺寸和不改变机构整体尺寸两种优化设计。通过比较，最终选定在不改变夹紧机构整体尺寸、仅改变内部杆件尺寸的优化作为最后优化结果，获得了各个变量的最佳设计参数，使夹紧机构的最大推进力由原先的1 567.56N减少到1 003.75 N，减少了36.0%，平均推进力由原先的723.7752 N减少到573.3304 N，减少了21.0%，大大节省了能源。同时完成了由经验设计向理论设计的转化。

［1］柴晓艳，余小巧.φ 406端面铣头倒棱机自动送料机构的优化设计 ［J］.重型机械，2010.

［2］李军，邢俊文，谭文浩.ADAMS实例教程［M］.北京:北京理工大学出版社，2002.

［3］陈树峰，马伏波.薄壁工件在夹紧力作用下变形量的计算 ［J］.煤矿机械，2005(2).

［4］华大年，华志宏.连杆机构设计与应用创新［M］.北京:机械工业出版社，2008.

［5］申永胜.机械原理教程 ［M］.北京:清华大学出版社，1999.

［6］秦大同，谢里阳.现代机械设计手册 ［M］.北京:化学工业出版社，2011.