前向楔角几何参数变化对隔离段工作特性影响

杨雨豪

(西北工业大学航天学院，陕西 西安 710072)

1 前言

隔离段是连接高超声速吸气式发动机进气道和燃烧室的重要部件，其工作原理是通过附面层分离产生激波串逐级压缩型面增压来流进行匹配燃烧室背压。

隔离段流动特征和工作特性对发动机整体性能影响极为敏感。评价隔离段的工作性能不仅要求能够尽量减少进气道压缩后气流的总压损失，并且还要具备较高的抗燃烧室反压能力，保证在一定燃烧室压力条件下隔离段内附面层分离点不会前移到进气道内，防止引起进气道不起动，捕获流量的急剧减小，导致发动机性能下降。国内外研究学者在提高隔离段性能方面开展了大量的研究工作，Kazuyasu.M等人［1］针对隔离段内激波串结构和附面层的相互作用进行了大量研究;Chung-Jen Tam等人［2］通过实验和数值模拟研究了采用附面层溢流的方式来提高超燃冲压发动机隔离段性能;考虑到实际工作条件，很多学者还研究了进气道、隔离段、燃烧室协同工作和波系相互干涉的研究［3-4］，另外还进行了在隔离段通过附面层吸除、增加热源以及采用主被动流动控制的方法来提高抗反压能力的研究［5-7］。但是当燃烧室背压过高时，较大的逆压梯度通过附面层上传，造成分离点向上游移动，而通过附面层溢流的方式就阻断了这种上移趋势，但是这种方式会造成流量损失，直接影响发动机工作效能。

同样在分离点附近设置台阶式几何结构体，也能起到抑制分离点前移的作用。通过这种方式如果能够保证隔离段稳定工作的基础上减少长度，则会对发动机的整体性能作出很大贡献，但是在高速气流中设置障碍物时，会产生较大的总压损失，因此实用的方法是采用前向楔角的方式来实现这一目的。

本文通过数值仿真的方法对不同构型不同参数的计算来研究隔离段内前向楔角结构参数变化对隔离段性能的影响规律，得出最大抗反压能力和总压损失系数，从而为隔离段几何构型的优化设计和实验方案确定提供依据，进而减小能量损失和总压损失。

2 计算方法

2.1 隔离段系统原理

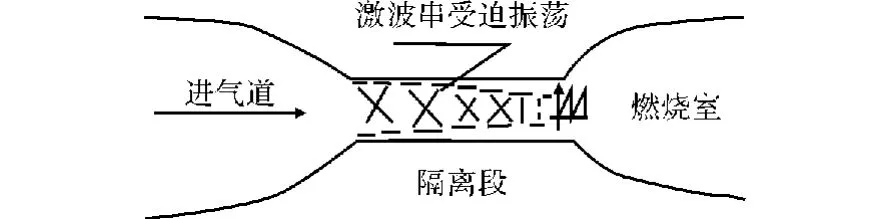
图1 隔离段工作原理Fig.1 Working principle of isolator

如图1所示，隔离段连接进气道和燃烧室，通过附面层分离产生激波串逐级压缩型面增压来流，从而匹配燃烧室背压的。从工作原理上分析，隔离段设计具有以下难点:

(1)需要隔离段进排气协调，能够满足在较大背压以及较短流道的情况下稳定工作，需具有较高的总压恢复系数;

(2)隔离段内具有流动复杂、多波系、跨声速的流动特点，波系之间以及波系和附面层之间有强烈相互作用。

因此，对数值计算方法需要具有较高间断面分辨率，以及准确的分离点识别能力。针对以上要求，本文流场求解利用有限体积法离散，定常雷诺平均N-S方程，各方程联立耦合隐式求解，对流项为二阶迎风格式，粘性项采用二阶中心差分格式，其它为一阶迎风格式。其中湍流模型采用Menter的SST k-ω模型。该模型将 k-ε和k-ω模型进行调和，在固体壁面附近采用Wilcox的k-ω模型，在自由流和边界层流外边界采用标准的k-ε模型，因此该模型对高雷诺数和低雷诺数同样适用，对混合流动、剪切流动模拟效果较好。壁面处理采用标准壁面函数法，标准壁面函数法假定:壁面附近粘性底层以外的地区，量纲速度服从对数率分布。

计算中涉及到三种基本边界条件，分别是入口压力远场边界，该条件的自由流马赫数以及静态条件已经给定，无反射;压力出口边界条件需要在出口边界处指定静压;壁面边界条件用于限制流体和固体区域，采用无滑移壁面和绝热条件。

计算结束条件为所有残差下降3个数量级且不再变化，关键截面流量不再变化表示计算结果收敛。

2.2 计算方法校验

本文中计算方法采用了文献［8-9］中的隔离段的实验和计算结果进行校验，文献中实验是在Wright-Patterson美国空军基地的18号实验室完成的，实验用隔离段采用了三种结构，本文仅对矩形结构的隔离段进行了校验，尺寸为4(W)×1.5(H)×25.75inch(L)。实验中来流马赫数为2.2，入口总压为50.0 psia，总温为530°R。图2给出了不同压力比条件下流道内波系结构纹影结果，从计算结果可以看出，随着压比的增加，第一道正激波的位置不断前传，当压比Rr=4.13时，波系被顶出入口，流道内全部形成亚声速流道，隔离段为不起动工作模式。图3给出了本文计算结果和文献中实验结果的对比，对比参数为壁面无量纲压比数值，从计算结果可以看出隔离段起动和不起动工作模式情况下隔离段壁面压强的分布规律。从计算结果可以看出，本文计算获得数据和文献中实验数据误差很小，所得到的流场波系结构清晰，具有较高的间断分辨率，能够准确模拟出流场中的分离位置、激波与附面层之间的相互碰撞反射等现象。表明本文采用的数值计算方法正确可靠，能够用于隔离段流场的计算分析。

图2 计算结果 (不同压力比条件下激波串纹影云图)Fig.2 Computational results(shock wave schlieren contour under different pressure ratio)

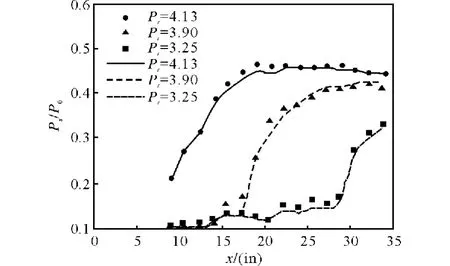
图3 本文计算结果和文献实验结果对比(壁面无量纲压比)Fig.3 Contrast between computational results and experimental results listed in refference(wall nondimensionalpressure ratio)

3 前向楔角的几何参数变化对隔离段流场特征和性能的影响规律

3.1 研究对象描述和基本参数定义

为了研究隔离段下游反向倾角对流场和抗反压能力的影响，本文针对图4所示的物理模型进行了数值模拟，其中来流为加热具有一定马赫数的纯净空气，隔离段总长度为L，入口高度为H，在距离入口长度为L1位置处，设置有对称的前向楔角，角度为α。

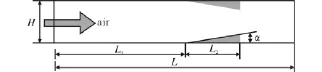
图4 物理模型示意图Fig.4 Schematic of physical model

本文通过以下几个参数来。评价下游带有前向楔角的隔离段的整体性能。

压比Pr，定义为出口静压和入口气流的静压之比，在隔离段启动工作模式下，此数值越大则表明其抗背压能力越强;分离点距离S，定义为入口和流道内附面层分离点之间距离，此距离越大，表明隔离段工作稳定性越好，具备一定的抗背压和来流不稳定能力;总压恢复系数π，定义为隔离段出口截面平均总压和入口截面平均总压之比，此数值越接近1，则表明隔离段的总压损失越小。

隔离段的整体性能需要同时用以上几个参数来综合评价，针对不同情况和应用目的来进行合理选择。

3.2 前向楔角几何参数对隔离段流场特征和性能的影响

为了分析隔离段下游楔角几何构型和相对位置对抗反压能力的影响规律，本文首先针对不带下游楔角的基本型隔离段进行了计算。其中入口高度H为50 mm，长度L为400 mm，入口马赫数为2，背压为入口静压的3.80倍。图5分别给出了该压比条件下激波串的压力和纹影云图，计算结果表明:由于背压的作用，在距离入口131.68 mm位置处形成了分离点，来流和附面层在分离点位置相互作用形成斜激波，斜激波经过反射后收于正激波，波后静压发生突跃，经过一系列激波串后，壁面静压逐渐增加，起到了抗反应能力的作用。总压恢复系数π为0.671。

图5 隔离段基本构型波系计算结果Fig.5 Computational results of shock wave system for basic configuration of isolator

通过对基本型隔离段的计算可以发现，在压比3.8条件下其分离点位置靠近上游，为了保证该隔离段具有一定的稳定工作裕度，以此分离点位置作为界限，其它构型的隔离段内分离点位置向上游移动位置超过此限制后，本文认为是不稳定状态。

在隔离段反压过高时，较大的逆压梯度通过附面层会向上游传递，当达到一定值时会使得附面层和壁面之间产生分离，分离点后会形成涡流，而分离点还会向上游移动，当到达一定条件时会稳定下来，为了保证隔离段能够稳定工作，本文拟通过在分离点下游一定距离来设置合理的前向楔角，起到阻断分离点前传的效果，并能够选择合理的几何构型来实现提高抗反压能力，尽量降低总压损失。

在计算分析之前，还需通过无粘管流的一维计算关系A/A*=f(M)来获得最大允许阻塞面积。本文条件下计算得到的临界阻塞面积比δ*为0.296，在设置前向楔角时其后缘高度不能超过此界限，图6给出了 H=50，L=400，L1=200，L2=25，α=11.32°构型条件下，压比Pr=3.8时的流场纹影计算结果。从计算结果可以看出，此条件下虽然面积阻塞比δ=0.2，小于临界面积比，但是隔离不能正常起动工作，在前向楔角上游完全为亚声速流动状态，在楔角之后形成了斜激波系，波系下游由于附面层分离又形成了另外一道斜激波系，最后反射终止于正激波，静压升高，总压恢复系数π为0.769。在此构型条件下，通过降低压比Pr并不能实现隔离段的起动工作状态，计算结果表明，随着压比Pr的减小，结尾正激波位置更靠下游，但此构型条件下隔离段不能起动，对于实际工作状态没有意义。

另外还通过改变L1、L2大小进行了分析，计算结果同样表明此阻塞比条件下隔离段不能正常起动工作，这表明实际流动状态下和无粘计算得到的结果有较大偏差，必须通过详细的数值模拟来进行计算。

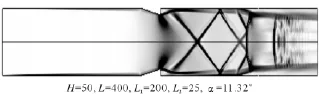
图6 构型压比3.8条件下波系计算结果Fig.6 Computational results of shock wave system under pressure ratio of 3.8

基本型隔离段的计算结果表明，在压比Pr为3.8条件下，在距离入口131.68 mm位置处形成了分离点，考虑到通过设置前向楔角来干扰附面层内逆压梯度上传，本文进行了前向楔角后缘位置靠近分离点构型的计算分析，即H=50，L=400，L1=125，L2=25，α=2.86°条件下，压比Pr为3.80。图7给出了马赫数和纹影云图的计算结果，从计算结果可以看出，分离点前移到楔角的前沿位置，距离入口为112.45 mm处，和基本型隔离段构型相比，并没有起到提高反压能力的效果，分离点前移意味着工作稳定区间的缩短，另外总压恢复系数为0.661，性能也低于基本型隔离段的。计算表明，前向楔角的位置不能过于靠前，否则对附面层的分离产生促进作用，导致其提前分离，从而影响隔离段整体性能。

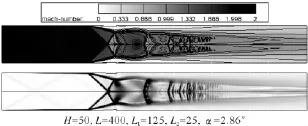
图7 构型压比3.8条件下波系计算结果Fig.7 Computational results of shock wave system under pressure ratio of 3.8

在减小面积阻塞比条件下，本文开展了前向楔角几何构型参数抗反压能力性能的计算分析。计算中通过改变不同的结构参数，通过考察不同压比条件下分离点位置以及总压恢复系数，来获得比较优化的几何参数。计算比较了多种构型组合的情况，针对隔离段能够稳定工作的工况，为了考察其抗背压能力，通过逐渐增加背压的方式让分离点前移并稳定在131.68 mm位置附近，此时的背压来作为其最大背压。图8给出了H=50，L=400，L1=150，L2=50，α =2.86°构型条件下考察最大背压情况下压力和纹影云图的计算结果。

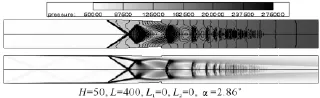
图8 构型压比4.11条件下波系计算结果Fig.8 Computational results of shock wave system under the pressure ratio of 4.11

从计算结果可以看出当压比Pr达到4.11时，分离点位置为138.41 mm，接近基本构型条件下压比Pr为3.80时的131.68 mm，因此可以认为此构型增大了隔离段的抗反压能力，但总压恢复系数为0.657，和基本型隔离段相比，总压损失增加。为综合考察楔角构型几何参数对抗反压能力的影响，本文还开展了改变楔角长度L2的计算分析，计算结果表明随着长度L2增压，抗反压先增加后减小，而总压恢复系数则单调减少。

由于在超声速气流中设置障碍物会引起较大的总压损失，隔离段的总压恢复系数也是其关键性能参数，根据已经计算的结果，本文还计算了减小前向楔角后缘高度对隔离段性能影响规律的数值仿真。图9给出了 H=50，L=400，L1=150，L2=50，α=1.43°构型，压比4.11条件下纹影云图的计算结果，表明该条件下分离点位置前移至130.02 mm处，总压恢复系数为0.659。另外还进行了H=50，L=400，L1=150，L2=50，α=0.72°构型下的流场计算分析，其保证分离点在131.68 mm位置附近时，最大压比为3.96，总压恢复系数为0.662。

综上计算分析可知，随着楔角后缘高度的减小，总压恢复系数增加，但抗反压能力呈现出先增加后减小的趋势。

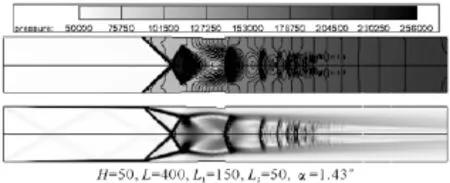
图9 构型压比4.11条件下波系计算结果Fig.9 Computational results of shock wave system under pressure ratio of 4.11

3.3 计算结果

表1给出了典型计算工况的几何参数和计算结果，为了研究改变楔角几何参数对隔离段抗反压能力和对总压损失的影响，特引入抗反压增益δPr和总压恢复增益系数δπ，其数值大小表示改变楔角几何参数后对抗反压和压力恢复的相对影响量。

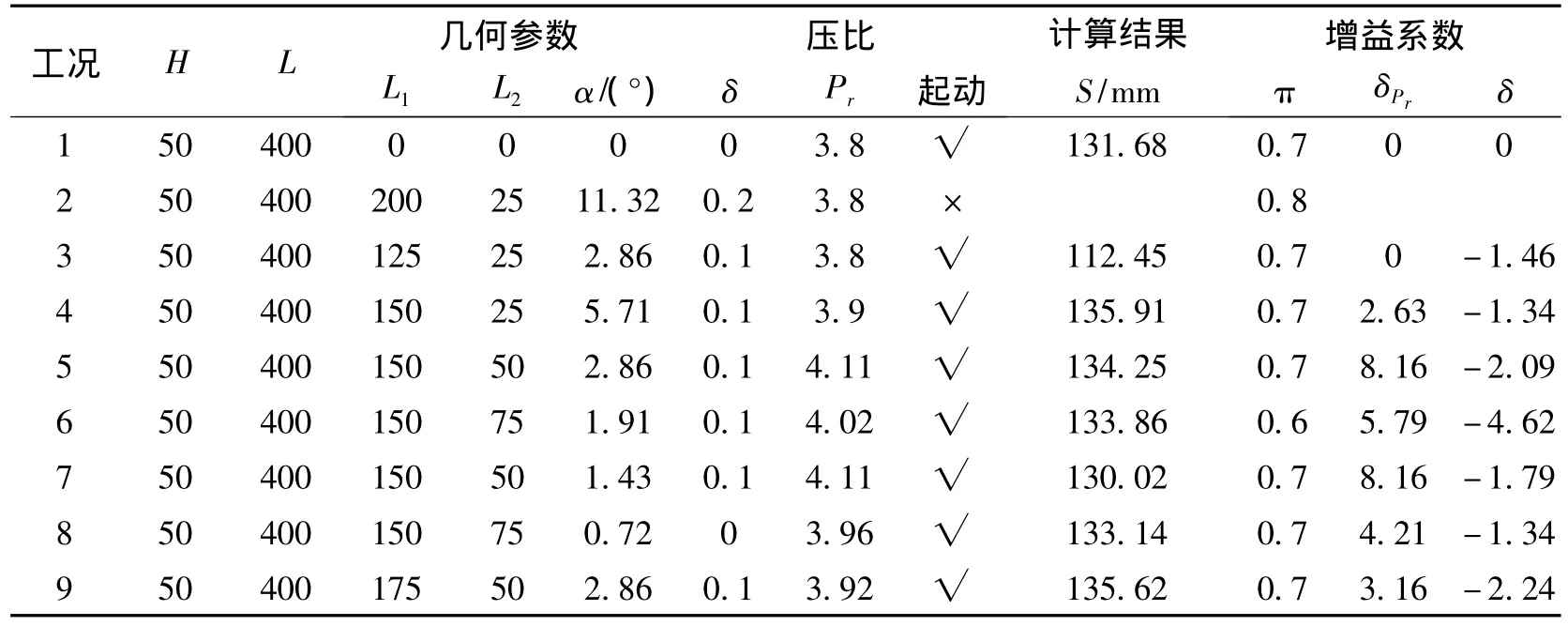
表1 计算工况和结果Tab.1 computation working condition and results

从计算结果可以看出，隔离段性能受各几何参数共同主导且相互牵制，尚不存在单调的影响规律，这也表明隔离段内本身流道状况复杂，微小几何变化都能引起的激波和附面层的强烈相互作用。但从固定位置和给定其它几何参数而分析单一几何参数变化时，能够反映出一些基本影响趋势，图10给出了楔角几何参数对隔离段性能影响规律，从曲线上可以看出，存在特定的楔角长度和角度使得隔离段抗反压能力最大，而随着楔角长度和角度增加，总压损失程度单调增加，但变化趋势略有不同。另外计算结果还表明，前向楔角前沿距离隔离段入口距离L1也存在优化值，对应较高的抗反压能力和较低的总压损失。

图10 楔角几何参数对隔离段性能影响规律Fig.10 Influence regulation of wedge angle geometrical parameters on isolator performance

在本文计算条件下，安装位置距离隔离段入口150 mm，楔角长度L2为50 mm，角度为1.43°时为较优构型，其抗反压能力增益较大，总压损失相对较低。这也给后续的楔角优化提供了限制范围，另外该楔角几何参数对不同来流条件的适应能力和工作性能也需要开展进一步的深入研究。

4 结论

通过本文研究，可以得到以下结论:

(1)本文采用的计算方法能够捕获到复杂激波串结构，具有较高的间断分辨率，能够准确模拟出流场中的分离位置、激波与附面层之间的相互碰撞反射等现象;

(2)合理的楔角几何结构能够提高隔离段的抗反压能力，存在优化的楔角长度、角度以及安装位置;但随着楔角长度和角度增加，总压损失单调增加;

(3)本文计算条件下，安装位置距离隔离段入口150 mm，楔角长度L2为50 mm，角度为1.43°时为较优构型，其抗反压能力增益较大，总压损失相对较低。

［1］Kazuyasu M，Yoshiaki M，Heuy-Dong K.Shock train and pseudo-shock phenomena in internal in internal gas flows［J］.Progress in Aerospace Sciences，1999(35):33-100.

［2］Saied Emami.Experimental investigation of inlet combustor isolator for a dual mode scramjet at a mach number of 4［R］.NASA Technical Paper(3502)，1995.

［3］Carroll B.F.，Dutton J.C.Multiple normal shock wave/turbulent Boundary-layer interactions［J］.Journal of Propulsion and Power，1992，8(2):441 －448.

［4］TU Qiuya，Corin S.Isolator/Combustion chamber interactions during supersonic combustion［J］.Journal of Propulsion and Power，2010，26(1):87－95.

［5］Chung-Jen Tam，Dean Eklund.Investigation of boundary layer bleed for improving scramjet isolator performance ［J］.AIAA Journal，2005，43(3):3286－3297.

［6］J.S.Shang，C.L.Chang，S.T.Surzhikov.Simulating HypersonicMagnetofluid-DynamicCompression in Rectangular Inlet ［J］.AIAA Journal，2007，45(11):1267－1274.

［7］J.S.Shang，C.L.Chang.Hypersonic Magneto-Fluid-Dynamic Compression in Cylindrical Inlet［J］.AIAA Journal，2007，45(9):3885－3891.

［8］K.-C.Lin，，C.-J.Tam.Characterization of Shock rain Structures inside Constant-Area Isolators of Model Scramjet Combustors ［J］.AIAA Journal，2006，44(7):3451－3458.

［9］K.-C.Lin，C.-J.Tam.Effects of Temperature and Heat Transfer on Shock Train Structures inside Constant-Area Isolators［J］.AIAA Journal，2006，44(5):817－824.