一种新的图像拷贝篡改检测方法

张 震，苏白娜，喻 宙

(郑州大学电气工程学院，河南郑州450001)

0 引言

区域拷贝篡改是图像篡改的常用手段之一，因此，对于该篡改的检测已成为图像真实性取证的研究热点［1］.笔者研究的对象即为区域拷贝篡改，其检测方法主要是依赖于图像子块的特征.文献［2］研究了这种篡改方法并利用块特征向量的字典排序提取篡改区域;文献［3-4］利用PCA变换减少块特征向量的维数以减少计算量，但是，图像子块在几何变换下不具有不变性.因此，对于有几何变换的拷贝篡改手段，以上算法失效.

基于David G.Lowe提出的SIFT(Scale Invariant Feature Transform)特征点对于图像的尺度和旋转保持不变性［5］，以及对于光照和3D视角的变化也能保持一定的稳定性，笔者结合LPP(Locality Preserving Projection)降维方法，为 SIFT特征点生成低维且有效的特征描述子.通过对描述子进行匹配，进而提出一种新的检测算法，即基于LPP-SIFT(Locality Preserving Projection-Scale Invariant Feature Transform)的检测算法.实验表明，该算法能够有效地检测出拷贝篡改图像，定位出拷贝源与篡改区域，且算法对于篡改区域的旋转、缩放具有不变性，对于噪声添加、JPEG压缩等操作具有较好的鲁棒性.

1 区域拷贝篡改模型

区域拷贝粘贴篡改是数字图像篡改的一个常用手段，它是为了覆盖图像中的部分内容而拷贝同幅图像中的某一区域并粘贴到另一不重叠的区域.这类篡改手段之所以应用广泛，是因为在同一幅图像中进行拷贝粘贴操作并不会导致图像的亮度、色彩等发生明显的变化，一般视觉上是无法察觉到的.

由于大多数检测算法对于区域块的旋转和缩放没有鲁棒性，所以一般参考文献中研究的模型只包含区域块的位移.而笔者研究的模型不仅包含了区域间的位移，还包含篡改区域的尺度变换以及旋转.

2 基于LPP-SIFT的检测算法

图像的特征点是其局部特征，在自然图像中不会存在相同的特征点［2］.因此，如果我们在一幅图像中检测到了大量互相匹配的特征点，可以判定该图像不是自然图像，而是通过区域拷贝篡改得到的伪造图像.根据匹配点对所聚集的区域，可以定位出拷贝源与篡改区域.

2.1 特征点的提取

笔者采用SIFT算法提取图像特征点.SIFT的全称是尺度不变特征变换，该变换可以将图像信息用相应的局部特征量来表示，旨在描述图像的局部特征，且对图像缩放、旋转甚至仿射变换都保持不变性.

SIFT算法包含四个步骤:尺度空间极值的检测、特征点位置的确定、特征点方向信息的确定、特征点描述子的生成［5］.在笔者提出的算法中，只用SIFT的前三个步骤来提取图像中的特征点，然后采用LPP降维算法为SIFT特征点生成低维的特征描述子.

2.2 变换矩阵的生成

虽然SIFT算法鲁棒性强，但由于描述器的维数太大，导致了匹配速度慢.因此，笔者采用LPP降维算法为特征点生成低维有效的特征描述器.

LPP算法相对于其他降维算法能够更好地保持数据集间的关系，以PCA(Principal Components Analysis)算法［6］与LPP对比为例，图1给出了两者降维效果的对比(以5维的数据样本集映射到2维空间为例).

图1 PCA和LPP对高维数据的映射效果对比Fig.1 Comparison result of PCA and LPP to map high-dimensional data

LPP是拉普拉斯特征映射算法的一种线性近似，该算法主要是通过求解变换矩阵对原始特征向量进行映射［7］，映射公式为:

式中:fi为原始的特征向量;f'i为降维后的特征向量.

本文算法中共选择了12幅图像来生成变换矩阵.首先，利用SIFT算法前三步生成了4 000个特征点;其次，在特征点周围提取37×37区域，计算每个像素的水平和垂直的梯度方向，生成一个高维向量，把它作为特征矩阵的一列;最后采用LPP算法求出变换矩阵.

2.3 特征描述子的生成

对于待检测图像，同样利用SIFT算法前三步生成特征点.以特征点为中心，选取37×37的区域，计算每个像素的水平和垂直的梯度方向，于是每个特征点生成一个2×35×35=2 450维的梯度向量，用fi表示.依据上述求出的变换矩阵A及公式(1)把梯度向量映射到低维的流形中，映射后的向量f'i作为特征点的描述器，本文实验中映射后向量维数为20.

2.4 特征点的匹配

最常见的特征点匹配方法是依据特征点描述子间的欧氏距离，但在Matlab中，计算向量间的点乘(内积)要比计算它们的欧式距离更有效.因此，本文实验中把向量角度比率的大小作为特征点匹配的判别准则，对满足最近邻域点和次近邻域点的向量角度比率小于设定值R的特征点进行匹配，得到匹配对.实验中可以改变参数R的大小以获取最佳匹配结果.

利用LPP-SIFT描述子找出匹配对需要两个特征向量集，所以对于一幅待检测图像，需要对生成的特征向量集进行划分，然后进行匹配运算，具体的步骤如下:

(1)设特征向量集包含M个特征点，如果M=1，则停止匹配;否则，在特征向量集中随机选取M/2个特征向量，定义为子集S1，余下的M/2个定义为子集S2;

(2)对S1和S2按照上述匹配准则进行匹配，对匹配的特征点对做出记号(本文中是用直线将其连接);

(3)对特征向量子集S1，递归执行上两步;对特征向量子集S2，也递归执行上两步;

(4)根据上述匹配，得到所有的匹配点对.

本文实验中，对于待检测图像中存在的匹配点对，用直线段将其标记出来.因此，如果标记的线段明显集中于某两个区域之间，则可以判定该图像被拷贝粘贴篡改过，匹配点对集中的两个区域，即为拷贝粘贴区域.

3 实验结果

本文所有实验都是在Matlab2008中实现的，实验所选的图像部分是来自于网络，另一部分是由作者自己拍摄的.本文算法对拷贝粘贴篡改图像的检测结果如下:

(1)对经历了尺度缩放的篡改图像进行检测.本组实验图2、图3中篡改图像的拷贝篡改区域分别经历了放大、缩小操作.

采用本文算法对图2中拷贝区域经历了放大的篡改图像进行检测时，实验发现参数R的最佳取值为0.65，正确匹配点对的数目是29，检测结果如图4(a)所示，此时的匹配点对数目比之前都大，且不存在误判点.表1给出了不同R值对图2(b)进行检测时的匹配点对数目的变化情况.对图3中拷贝区域经历了缩小的篡改图像进行检测时，R的最佳取值为0.4，此时匹配点对的数目是16，检测结果如图4(b)所示.表2给出了不同R值对图3(b)进行检测时，匹配点对数目的变化情况.实验表明，本文算法能够有效地检测定位拷贝区域经历了尺度缩放的篡改图像.

表1 R值变化时尺度放大图像的检测结果Tab.1 Detection results with different R

(2)对经历了旋转、JPEG压缩的篡改图像进行检测.本组实验的原图像是由作者自己拍摄的自然图像，篡改图像中的拷贝篡改区域经历了旋转操作，且图像经历了压缩因子Q=30的JPEG压缩操作，采用本文算法对篡改图像的检测结果如下:

采用本文算法对图5(b)进行检测时，参数R的最佳取值为0.7，此时匹配点对的数目是12，检测结果如图6所示.表3给出了不同R值对图5(b)进行检测时，匹配点对数目的变化情况.实验表明，本文算法对于旋转和JPEG压缩具有很好的鲁棒性.

表2 R值变化时尺度缩小图像的检测结果Tab.2 Detection results with different R

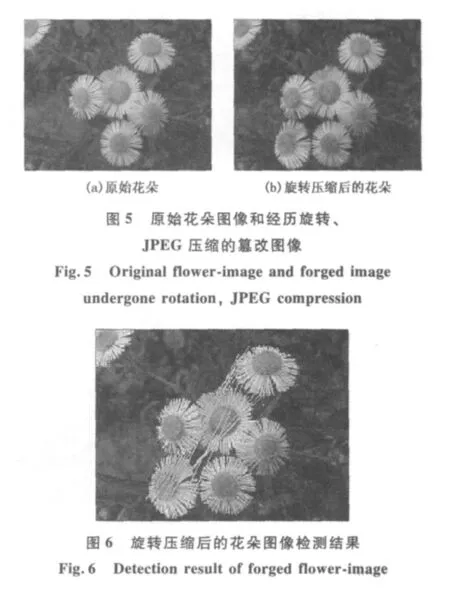
表3 R值变化时旋转压缩后图像的检测结果Tab.3 Detection results with different R

(3)对经历了旋转、JPEG压缩、加噪的篡改图像进行检测.本组实验的目的是验证本文所提出的算法对于噪声是否具有鲁棒性.为了对比效果，本组实验依然选用第二组实验中的图像，即对图5(b)所示的篡改图像添加了PSNR(Peak Signal to Noise Ratio)=30 dB的高斯白噪声，然后检验本文算法的检测效果.

经实验检测，发现本组实验中参数R的最佳取值依然为0.7，此时匹配点对的数目是12，没有误判匹配对.表4给出了对加噪图像进行检测时，不同R值的特征点匹配情况.

表4 R值变化时对加噪图像的检测结果Tab.4 Noised image detection results with different R

将本组实验的检测结果与第二组中的检测结果进行对比，可以看出，本文算法对于加噪后的篡改图像依然有效，而且检测效果与第二组的检测效果相差很小.从实验结果可以看出，本组中参数R的最佳取值与第二组相同，即R=0.7，此时匹配点对的数目也是12.通过表4与表3的对比可以证明:本文算法对于噪声具有较好的鲁棒性.

4 结论

笔者提出的基于LPP-SIFT的拷贝篡改检测方法，能够有效地检测出同幅图像间的拷贝篡改区域.相对于SIFT的128维特征描述子，本算法的描述子只有20维，维数有了大幅度的减少，因而在很大程度上减少了特征点匹配时的运算量，提高了检测速度.笔者提出的区域拷贝篡改图像检测方法，不仅能够有效地检测拷贝篡改图像，还能准确地匹配出拷贝源和篡改区域.实验证明，该算法对于尺度缩放、旋转、缩放、噪声添加以及JPEG压缩操作具有很好的鲁棒性.

［1］ 吴琼.面向真实性检测的数字图像盲取证方法研究［D］.长沙:国防科学技术大学信息系统与管理学院，2008.

［2］ FRIDRICH J，SOUKAL D，LUKAS J.Detection of copy-move forgery in digital images［C］//Proceedings of Digital Forensic Research Workshop.Cleveland:IEEE Computer Society，2003:5-8.

［3］ POPESCU A C，FARID H.Exposing Digital Forgeries by Detecting Duplicated Image Regions［D］.Hanover:Department of Computer Science，Dartmouth College，2004.

［4］ JU Sheng-gen，ZHOU Ji-liu，HE Kun.An authentication method for copy areas of images［C］//Proceedings of the 4th International Conference on Image and Graphics.Chengdu:IEEE press，2007:303-306.

［5］ LOWE D G.Distinctive image features from scale-invariant key points［J］.International Journal of Computer Vision，2004，60(2):91-110.

［6］ YE K，SUKTHANKAR R.PCA-SIFT:a more distinctive representation for local image descriptors［C］//Proceedings of the 18th International Conference on Pattern Recognition.Washington:IEEE press，2004:506-513.

［7］ HE Xiao-fei，NIYOGI P.Locality Preserving Projections［DB/OL］.http://wenku.baidu.com/view/d6c 659bd960590c69ec376e9.html.2011-03-11.