基于α截集法的生土窑居模糊随机可靠度分析
郭平功,童丽萍
(1.郑州大学 土木工程学院,河南 郑州450001;2.河南城建学院土木工程系,河南平顶山467036)
0 引言
生土窑居是在原始黄土中挖凿而形成的穴居居住形式,由挖凿成型的纯原状土拱作为窑居的自支撑结构,没有栋梁支撑,也没有其它支护.但却能够久而不衰、屹立百年甚至数百年而不坍塌.即使在地震多发区(中国在役窑居大多分布于地震多发地带,45%的窑居区地震烈度在7度以上),建造年代百年以上的窑洞也很普遍,充分说明了生土窑居较高的可靠性.只有从可靠度角度对生土窑居进行研究,才能揭示其可靠性较高的原因.
目前还没有关于生土窑居可靠度研究的文献.影响其可靠度的主要因素为土体的强度.土体力学性能参数主要的获取方法是试验,由于土体本身在空间上呈现很大的变异性,以及取样的扰动、试验方法的差异,使试验结果具有不确定性,主要是随机性和模糊性[1-2].由于土体力学参数的随机性和模糊性,导致生土窑居的可靠度具有随机性和模糊性.
目前,考虑模糊不定性的研究方法仍处于探索阶段,α截集法、凸集法、模糊集法、主观概率法、混沌理论法等都被用来进行模糊分析[3].由于α截集法能同时考虑模糊性和随机性[4],笔者拟基于α截集法进行生土窑居的模糊随机可靠度分析.
通过α截集法,将土体模糊的力学参数转化为分布在一定区间上的离散数,结合强度折减有限元法,构建生土窑居的功能函数,进而求得模糊随机可靠度,探索土体力学参数的模糊性对生土窑居可靠度的影响.
1 基于α截集法的土体模糊参数[5]
设生土窑居土体模糊参数的均值为对称三角形模糊数[xB,xN,xT](图1),取某一α 截集(0≤α≤1),则其离散结果为区间数图中,xN为模糊数的均值分别为 α 截集上的模糊数的左右两个端点值,α =0 时的可简记为xB,xT.对于对称三角形模糊数,在α截集上有如下关系式:

式中:σ为参数的标准差,反映参数随机性的大小;f为模糊程度系数,反映参数模糊性的大小.依据专家知识及工程经验,f∈[0.5,1.5][6].
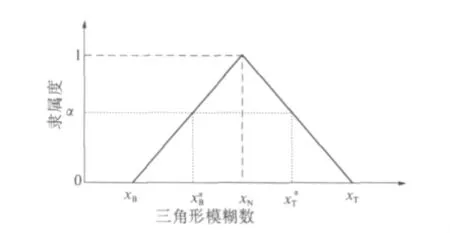
图1 三角型模糊数及其隶属度Fig.1 Triangular fuzzy number and its membership degree
根据河南三门峡陕县生土窑居所在的黄土土层分布,结合中国市政工程西北设计研究院有限公司进行的土工试验,取陕塬(历史上对陕县黄土塬的简称)的黄土力学参数平均值如表1所示.

表1 黄土力学参数平均值Tab.1 Average mechanical parameters of loess
参照文献中有关土工参数的变异系数δ的资料[7],除容重的变异系数较小,约为0.03,其它参数的变异系数δ的取值范围为δ∈[0.1,0.3],可将参数的标准差记为σ=δ·xN,式(1)可写为:

以黏聚力X1、内摩擦角X2两个不相关的正态模糊随机变量为例,模糊数的均值分别为51.8 kPa、28.1°,二者采用相同的变异系数 δ,则在α截集上,X1的端点值分别为的端点值分别为28.1(1+(1- α)fδ).所以 α 截集上模糊随机变量(X1,X2)的两种极值组合为在两种组合下进行随机可靠度分析,可求得α截集上可靠指标的极小值和极大值,亦可求得对应的设计验算点可见通过α截集法这一桥梁,模糊随机可靠度问题转化为了随机可靠度问题.
2 生土窑居响应面函数的构建
笔者采用响应面函数代表生土窑居的功能函数,输入为土体的力学性能参数,“响应”采用“富裕安全系数”,由生土窑居的有限元模型计算求得.
2.1 有限元分析模型
由文献可知[8],生土窑居可按平面应变问题研究.选取三联孔模型,每孔窑室的尺寸相同,中间主窑两侧的窑腿宽度相同.根据在河南三门峡陕县的调研,窑居的几何参数取平均值,如图2、表2所示.为减少计算量,取对称的一半模型进行有限元建模如图3所示,根据圣维南原理,有限元分析模型的总尺寸取窑室尺寸的5倍以上.由于模型较大,图3中截取的是有窑洞的部分.图3(a)中窑洞未开挖,施加了重力荷载并平衡了初始地应力.

图2 生土窑居各部位示意图Fig.2 Sketch map of earth-sheltered dwelling

表2 生土窑居几何参数Tab.2 Geometry parameters of earth-sheltered dwellings

图3 有限元分析模型Fig.3 Model of Finite Element Analysis
生土窑居的营造不同于一般建筑,它不是加荷,而是经历了卸荷——加荷的过程.窑室的开挖使初始的自重应力场发生了应力重分布,并且各窑室的开挖不是同时完成的,有的经历数年,窑室开挖完成后(如图3(b)所示),施加地面均布荷载4 kN/m2×1.4=5.6 kN/m2,其中1.4为可变荷载分项系数,标准值取4 kN/m2是考虑到地面经常有车辆行驶或停留,参考《建筑结构荷载规范》GB 50009—2001中关于楼面作为汽车通道及停车库的荷载取值.
靠近窑室的部分网格划分的较密,离得越远网格划分越粗.模型右侧为对称约束,底部固定竖向约束,左侧固定水平约束.
每轮有限元分析的输入参数为土体的力学材料参数.首先全部力学参数均作为随机变量输入,可求得各随机变量的灵敏度系数,从中选择灵敏度系数较大的随机变量,作为模糊随机变量,再进行生土窑居的模糊随机可靠度分析.
2.2 基于强度折减法的富裕安全系数
采用“富裕安全系数”(以F'表示)作为响应面函数的“响应”,即代表功能函数在不同随机变量组合情况下的值,规定F'与安全系数(F)的关系式为:[9]

采用强度折减法确定结构的安全系数,其原理如式(4)所示.式中:w为强度折减系数;c、φ和c'、φ'分别为折减前后的黏聚力和内摩擦角;结构处于极限状态时的折减系数即为安全系数F.极限状态的判定以特征点的位移发生突变为标准.

对于图3的有限元模型,选取主窑拱圈的中点A作为特征点,当土体的力学参数均取表1所示的平均值时,特征点竖向位移与w的关系如图4所示.图中位移以向上为正.

图4 特征点竖向位移与强度折减系数关系图Fig.4 Relation between vrtical dsplacement of caracteristic pint and srength reduction fctor
由图4可知,折减系数由1.58增大为1.59时,向下位移由48 mm增大为98 mm,发生突变,说明w为1.58时窑居处于极限状态,安全系数F为 1.58,F'为 0.48.
2.3 响应面函数
本文的响应面函数采用不含交叉项的二次多项式.当只有黏聚力、内摩擦角两个模糊随机变量时,其形式如式(5)所示.
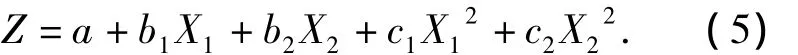
式中:a、b1、b2、c1、c2为待定系数.求解响应面函数,转化为求(5)式中的待定系数,需首先确定一系列试验点,并按上文2.1和2.2节所述建立有限元模型,求得富裕安全系数F',即求得与试验点对应的功能函数值.本文的试验点采用坐标轴上的点的中心进行复合设计.
每轮有限元计算,响应面函数的获取按如下步骤进行:①按照各试验点的数据进行有限元建模计算,求得对应的F';②解线性方程组,获取待定系数 a、b1、b2、c1、c2,即求得该轮有限元计算的响应面函数.
每轮得到响应面函数后,即可按照改进的一次二阶矩法求得可靠指标与验算点,当前后两轮所得验算点的模满足(6)式时,迭代终止.

3 生土窑居的模糊随机可靠度
3.1 土体参数中关键的模糊随机变量
土体的力学参数如表1所示共有5个,如果都作为模糊随机变量,计算代价较高,可进行常规随机可靠度分析,求得各参数的灵敏度系数,以灵敏度系数大者作为模糊随机变量.
各参数的均值取表1数据,容重的变异系数取为0.03,其它参数的变异系数取为0.3[7],基于强度折减法建立响应面函数,进而求得可靠指标与灵敏度系数,各参数的灵敏度系数如表3所示.

表3 各参数的灵敏度系数Tab.3 Sensitivity coefficient of parameters
由表3可以看出,黏聚力和内摩擦角的灵敏度系数绝对值远大于其它参数,二者可作为模糊随机变量,进行生土窑居的模糊随机可靠度分析.其中灵敏度系数是负数的为抗力项,正数的为荷载项.
3.2 生土窑居的模糊随机可靠度
模糊随机变量表示为(X1,X2),其模糊均值为表1所示的黏聚力和内摩擦角的取值,在不同的模糊系数f、变异系数δ情形下,可得(X1,X2)的两种极值组合为,二者均对应式(4)中未折减、初始的(c,φ),基于强度折减法建立响应面函数,可求得α截集上可靠指标的极小值和极大值,亦可求得对应的设计验算点当f、δ在其常见范围内变化,即取 f∈[0.5,1.5],δ∈[0.1,0.3]时,模糊可靠度的计算结果如图5~6所示.
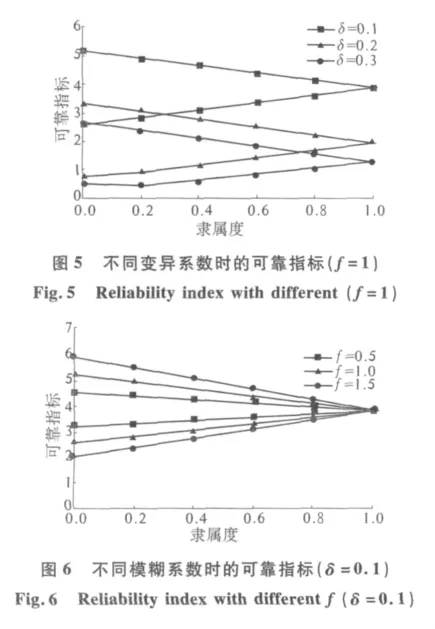
由图5、图6可知,模糊随机可靠指标不是一定值,而是分布在一个三角形的区域,这是因为在α截集上,模糊随机参数是呈三角形分布的;当隶属度为1时,模糊随机可靠指标退化为随机可靠指标,成为一定值;在隶属度小于1时,模糊随机可靠指标在一闭区间上分布,且隶属度越小,该闭区间的跨度越大,但闭区间的中点均为隶属度为1时的模糊随机可靠指标,这是因为模糊数是呈对称三角形分布的.
由图5可知,当δ由0.1增大为0.2时,模糊随机可靠指标的中值(即隶属度为1时的值)由3.86减小到1.93,相应的失效概率由5.67e-5增大为2.68e-2,即失效概率增大了约470倍,说明土体黏聚力和内摩擦角变异系数的增大,将导致生土窑居可靠度的急剧降低;δ为0.3时,生土窑居最小的失效概率约为1/250,是很大的.
由图6可知,模糊程度系数f的变化,不影响模糊随机可靠指标的中值;随着模糊程度系数f的减小,可靠指标分布的闭区间跨度越来越小,并且可得出推论,当f=0时,即模糊程度为0时,模糊随机可靠指标退化为随机可靠指标;当f=0.5、δ=0.1时,模糊随机可靠指标的最小值为3.20,生土窑居仍是可靠的,与模糊随机可靠指标三角形分布对应的土体黏聚力取值范围是[49.21 kPa,54.39 kPa],内摩擦角的取值范围是[26.70°,29.51°].
3.3 原始正态随机空间中的模糊验算点
原始正态随机空间是指正态随机变量未经标准化处理的空间.计算表明,无论f、δ及α如何取值,生土窑居的模糊验算点均为(33.73±1.24 kPa,23.47 ±0.9°),验算点的粘聚力和内摩擦角仅在很小的范围内浮动,在验算点的平均值处(33.73 kPa,23.47°),F'为 0,说明验算点是准确的,出现上下微小浮动是和(6)式的迭代收敛准则对应的,该精度已满足工程要求.
在标准正态随机空间中,不同的f、δ及α取值,验算点的坐标差异很大,而回归到原始正态随机空间中,其坐标均非常接近(33.73 kPa,23.47°),可见在标准正态随机空间中呈现出的验算点,更显示出“模糊”的特点,而事实与此相反,在生土窑居的几何参数等为定值的条件下,只考虑土体黏聚力和内摩擦角的模糊随机性,模糊验算点为一定值.
模糊验算点为定值与事实相符,生土窑居在什么样的土体材料参数下处于承载能力极限状态,不与所采用的土体模糊随机参数相关.
而模糊随机可靠指标之所以在一定区间上分布,呈现出“模糊”的特点,是因为验算点在标准正态随机空间中的坐标与土体模糊随机参数相关,而可靠指标为验算点在标准正态随机空间中到原点的距离.
3.4 黏聚力和内摩擦角的灵敏度系数
计算表明,无论f、δ及α如何取值,如果保留到小数点后一位数字,黏聚力和内摩擦角的灵敏度系数分别为-0.9和-0.4,二者均为抗力项,即随着两个参数的减小,生土窑居将接近承载能力极限状态,并且和3.1节的结果一致,可见模糊随机可靠度分析并不改变二者对可靠指标的影响程度.
同时说明,黏聚力对可靠指标的影响程度更大.在陕塬,经常可见近乎直立的黄土峭壁,充分说明该种黄土材料的粘聚力较大,适宜建造生土窑居.
4 结论
通过α截集法,将黄土的力学参数的模糊分布离散在区间上,把模糊随机可靠度问题转化为随机可靠度问题,经过多轮有限元分析,结合强度折减法,构造生土窑居的响应面函数,求得模糊随机可靠指标与验算点,所得结论如下:
(1)α截集法是将模糊随机可靠度问题转化为随机可靠度问题的桥梁,且其参数中包含模糊系数f、变异系数δ,即能同时考虑模糊性和随机性的影响,用来描述黄土力学参数的模糊分布是合适的.
(2)基于强度折减法的富裕安全系数,从整体上描述了生土窑居的安全性,可认为生土窑居是一构件,避免了把生土窑居这一复杂系统划分为串联、并联构件的问题,使求其模糊随机可靠度这一问题变为可能.
(3)河南三门峡陕县的生土窑居在营造过程中,十分注意选址,黄土材料力学参数的模糊性和变异性均较小,生土窑居的可靠性较高、选址合理.
(4)模糊随机可靠指标不是一定值,而是分布在某个区间,即生土窑居的失效概率在一定的范围,更符合真实的情况.
(5)土体材料参数变异系数的增大,将导致可靠指标的迅速减小;模糊系数的增大,将导致模糊可靠指标分布范围变大.
(6)在生土窑居的几何参数和荷载条件为定值的情况下,关于土体参数的验算点为定值(33.73kPa,23.47°),不呈现“模糊性”.
(7)黏聚力比内摩擦角对可靠指标的影响更大,在生土窑居营造时,选址应选择黏聚力大的黄土区域.
[1] SHIRAISHI N,FURUTA H.Reliability analysis based on fuzzy probability[J].Journal of Engineering Mechanics,1983,109(6):1445-1459.
[2] MOENSD,VANDEPITTE D.A survey of non-probabilistic uncertainty treatment in finite element analysis[J].Computer Methods in Applied Mechanics and Engineering,2005,194(12-16):1527-1555.
[3] MÖER B,GRAF W,BEER M.Safety assessment of structures in view of fuzzy randomness[J].Computers& structures,2003,81(15):1567-1582.
[4] 谭晓慧,胡晓军,储诚富,等.模糊响应面法及其在边坡稳定可靠度分析中的应用[J].中国科学技术大学学报,2011,41(3):233-237.
[5] FENGY H,HU L J,SHU H S.The variance and covariance of fuzzy random variables and their applications[J].Fuzzy Sets and Systems,2001,120(3):487-497.
[6] GIASI C I,MASI P,CHERUBINI C.Probabilistic and fuzzy reliability analysis of a sample slope near Aliano[J].Engineering Geology,2003,67(3-4):391-402.
[7] 朱小林.土体工程[M].上海:同济大学出版社,1998:86-109.
[8] 童丽萍,韩翠萍.传统生土窑洞的土拱结构体系[J].施工技术,2008,37(6):113-115.
[9] 张永兴,胡居义,何青云,等.基于强度折减法小净距隧道合理净距的研究[J].水文地质工程地质,2006(3):64-67.

