粉煤灰砖砌体轴压本构关系试验研究
杨卫忠,曹文文,王 茜
(郑州大学土木工程学院,河南郑州450001)
0 引言
砌体结构的理论研究离不开试验研究,而试验结果则为结构基本力学性能的研究提供依据,也是对理论模型进行验证的有力手段.砌体在轴心受压时的应力-应变曲线不仅是砌体结构分析的重要基础,同时还是其力学性能的集中体现.目前,国内外对于砌体应力-应变曲线尤其是全曲线的研究较少且相对滞后[1].在普通试验机上进行砌体抗压试验时,由于试验机本身刚度不足,超过最大应力后试件会被迅速压坏,呈脆性破坏特征,无法测出下降段,常用方法是在试验机上附加刚性元件以实现应力-应变曲线的下降段[2-3].为此,本试验也采用此类方法,在试件两侧布置同步千斤顶与试件共同受力,以量测应力-应变全曲线的下降段.
为了验证砌体随机损伤本构关系的理论研究结果,同时,也为了研究模型参数,以粉煤灰实心砖砌体为研究对象,进行了砌体轴压本构关系的试验研究,共设计了3组棱柱体试件,每组3个试件,变化的参数是砂浆强度,除了考察该类砌体在单轴单调受压状态下的强度、裂缝发展、破坏形态外,重点考察其应力-应变曲线特征,为后续的随机损伤本构关系提供可靠的数据.
1 试验概况
试验用砖为粉煤灰实心砖,平均尺寸为202 mm×96 mm×51 mm,砂浆采用水泥砂浆,通过改变灰砂比来控制砂浆强度,从而实现不同的砌体强度.
按《砌体基本力学性能试验方法标准》[4]规定的高厚比β=3来确定砌体受压试件的外形尺寸为202 mm×310 mm×610 mm(厚度×宽度×高度),试件厚度和宽度的允许误差为±5 mm,顶部用厚度为10 mm的1∶3水泥砂浆找平,并采用水平尺检查其平整度,采用水平砌筑,块体的排列方式如图1所示.

图1 试件侧面及横截面Fig.1 Section of specimen
每组试件灰缝厚度10~12 mm,每种配比砂浆采用同一盘足量砂浆并制作一组(3个)砂浆试件,以便测定砂浆强度.砂浆试件采用70.7 mm×70.7 mm×70.7 mm的无底试模制作,人工振捣.砌体试件和砂浆试件均在自然条件下养护28 d后进行试验.
试验装置如图2所示,试件宽侧面两侧放置同步千斤顶,窄侧面两侧放置百分表,百分表架在钢垫板与试验机底座之间.

图2 试验装置Fig.2 Device of test
加载时,在预估破坏荷载的5%区间内,反复预压2~3次.预压后正式加压,分级加载,每级为破坏荷载的5%,保持匀速加载,试验过程中观察第一条受力的发丝裂缝,并记录初裂荷载值.开裂后,仍然按照每级5%的破坏荷载加载,当构件上的传感器在应变仪上显示的读数开始下降时,表明试件将逐渐丧失承载力而进入破坏阶段,此时暂停加载并记录下试件受到的压力值,即极限承载力.然后继续加载,试件的承载力会随着应变的增加而减小,但由于千斤顶与试件共同受力,在试件的承载力减小之后,试验机的压力会向两边的千斤顶转移,这样就避免了积蓄在试验机内的应变能迅速释放造成的试件脆性破坏.但在本试验中,为得到较长的曲线下降段,当试件承受荷载为破坏荷载的50%左右时才停止试验.加载过程中,需记录下每级荷载下的变形值.
按本试验方案进行全曲线试验的关键点有两个:其一是控制千斤顶何时受力,刚开始加载时,试验机上压板与千斤顶不接触,只有试件受力,当超过破坏荷载的10%时,让千斤顶顶住试验机上压板,使试件和千斤顶共同受力;其二是控制好加载速率,匀速加载,特别是曲线进入下降段后,要缓慢加载以防止试件突然崩裂.
2 试验现象及主要结果
2.1 试验现象
根据裂缝的发展情况,将砌体试件从开始受压到最终被压碎的整个过程分为3个阶段:
第一阶段,未出现裂缝.从试件开始受压到裂缝出现之前,百分表读数随荷载的增加而增加,但试件表面无任何变化,且荷载不增加,百分表读数也保持不变.
第二阶段,开始出现裂缝,但裂缝的发展处于稳定阶段.当荷载达到某一值,首先在某一单砖出现发丝裂缝,此时的荷载为破坏荷载的54% ~77%,平均为69%,与普通砖砌体的50% ~70%大致相当.随荷载的增加,单砖内的裂缝逐渐向上下延伸开展,并在其它砖内也开始出现裂缝.此时,裂缝发展尚处于稳定阶段,即荷载不增加,百分表读数也保持不变.
第三阶段,裂缝迅速发展的不稳定阶段.当荷载达到破坏荷载的80% ~90%时,裂缝迅速发展并沿竖向贯通数砖,明显延长加宽,并伴有开裂的声音.此时,即使保持荷载不变,裂缝也会继续发展,如图3(a)所示.百分表的读数变化较快.继续加载,试件的表面或角部会出现脱皮、外鼓、掉块等现象,贯通的竖向裂缝将砌体分割成若干独立的小柱,至此,试件丧失承载力,达到其极限破坏状态.破坏成小柱体的试件如图3(b)所示.

图3 裂缝及破坏Fig.3 Cracks and failure mode
2.2 强度
表1列出了试件的开裂荷载和极限荷载,同时,试验前对试件截面尺寸进行了测量,取其平均值,则按《砌墙砖试验方法》[5]来测定砖的抗压强度,如表1所示.按现行《砌体结构设计规范》[6]计算的砌体受压强度理论值fm也列于表1.
2.3 应力-应变曲线
根据百分表上读取的每级荷载下的变形值,通过计算,可以得到每一组粉煤灰砖砌体试件的实测应力-应变曲线,如图4所示.曲线进入下降段之后,应变不断增加的同时,应力迅速下降,相对于应变轴,曲线的走势由凸变凹,出现反弯点.应变进一步增加,应力降低减慢,曲线变平缓,进入残余强度阶段.实际结构中,此时的构件已失去意义.
由图4不难发现,随着砂浆强度增加,即砌体强度提高,而峰值应变呈降低趋势,这也与其它块体材料砌体变形规律相符.
进一步对实测应力-应变曲线进行均一化处理,结果如图5所示,ε0为峰值应力σmax对应的应变.从图中可以看出,所有试件均一化后的应力-应变全曲线的上升段和下降段具有内在的相似性.
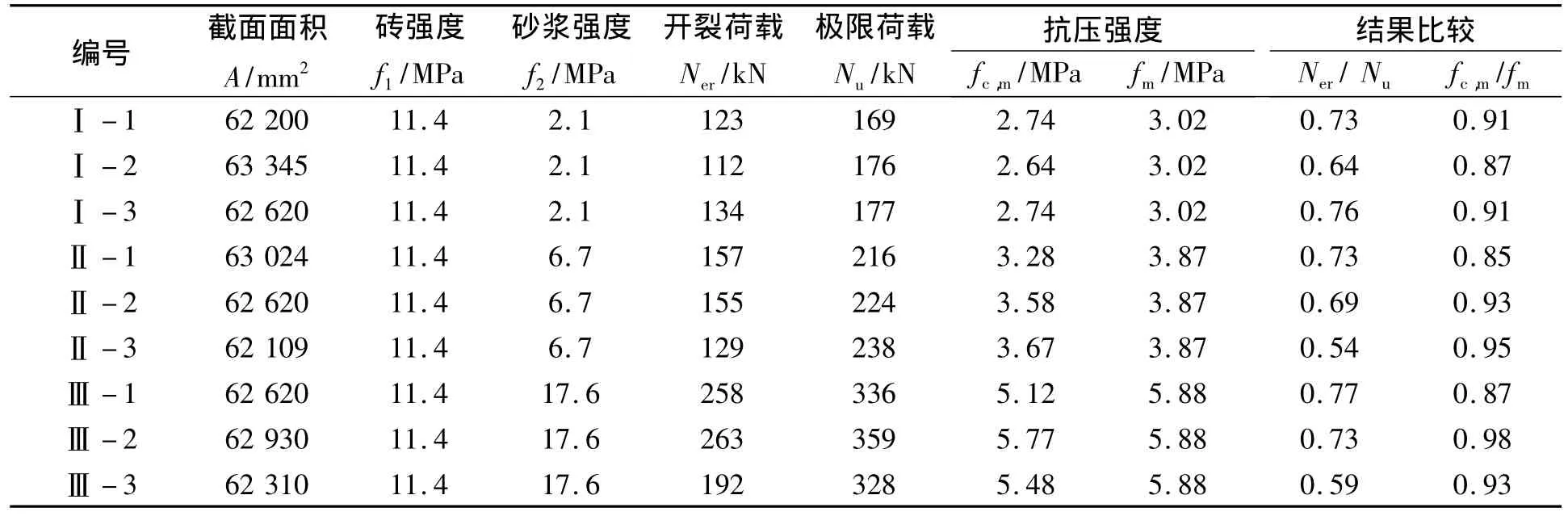
表1 强度试验结果Tab.1 Results of compression strength

图4 实测应力-应变曲线Fig.4 Stress-strain curves of test result

图5 均一化的应力-应变曲线Fig.5 Relative stress-strain curves
3 结果分析与讨论
3.1 强度分析
从表1中不难看出,理论抗压强度值fm略高于实测砌体抗压强度值fc,m,偏高约9%.其原因包括:砂浆的和易性(和易性差则灰缝不易饱满均匀),砂浆的变形性能(变形率增大会降低砌体的抗压强度),砌筑质量(灰缝均匀饱满程度、灰缝厚度、砖的含水率等),试件偏心受压或局部受压(试件没有完全对中或顶面抹灰不平整)等等.此外,式(1)本身也是个经验公式,且主要针对砖砌体.
3.2 应力-应变关系
作者曾借助细观模型,从损伤角度建立统一本构关系模型[7],并初步验证了其合理性.其本构关系如下:

式中:Em为砌体的弹性模量;λ,ζ为随机场参数;δ为变形系数,反映微裂缝面拉开或滑移的程度.
上述参数可结合试验,采用随机建模原理并借助于Powell优化算法即可识别.表2即是模型参数的识别结果[8].图6给出了采用式(1)~(3)得到的理论结果与上述3组试件均值曲线的比较.
从图6中不难看出,基于细观损伤单元模型建立的轴压砌体损伤本构关系能较好地预测试件的受力全过程应力响应.
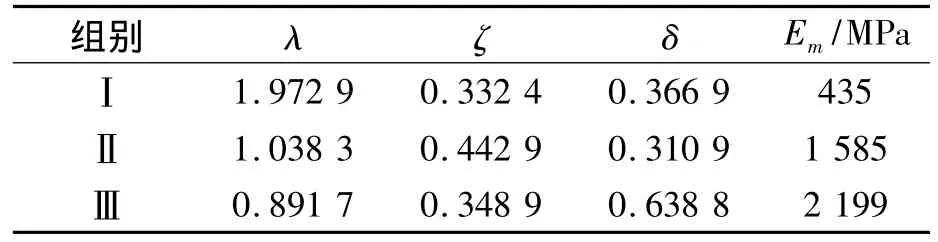
表2 参数识别结果Tab.2 Coefficients in the constitutive model

图6 应力-应变曲线的理论值和试验值比较Fig.6 Comparison of mean stress-strain curves between experiments and analytical results
4 结论
(1)采用普通试验机加千斤顶的装置,可以测得砌体在轴压状态下的应力-应变全曲线,关键点在于控制好加载速率,而试件顶面的平整度及受力均匀也是其重要条件.
(2)粉煤灰砖砌体受压时的裂缝发展及破坏形态与普通砖砌体相似,开裂荷载为破坏荷载的54%~77%,平均为69%,当荷载达破坏荷载的80% ~90%,则进入破坏阶段.
(3)随砂浆强度提高,砌体受压强度和弹性模量也增加,但应力-应变曲线的形状变化不大,而峰值应变降低.
(4)现行《砌体结构设计规范》(GB50003)预测的粉煤灰砖砌体抗压强度偏高约9%.
(5)粉煤灰砖砌体受压应力-应变关系可采用基于细观损伤模型而建立起的本构关系预测.
[1] 刘桂秋.砌体结构基本受力性能的研究[D].长沙:湖南大学土木工程学院,2005.
[2] 刘立鹏,翟希梅,张连振,等.砌体材料的应力-应变关系[J].低温建筑技术,2007(6):63-65.
[3] 郝彤,刘立新,巩耀娜.混凝土多孔砖砌体受压应力-应变全曲线试验研究[J].建筑结构,2008,38(10):73-74.
[4] 中华人民共和国建设部.GBJ 129—90,砌体基本力学性能试验方法标准[S].北京:中国建筑工业出版社,1991.
[5] 中华人民共和国建设部.GB/T 2542—2003,砌墙砖试验方法[S].北京:中国标准出版社,2003.
[6] 中华人民共和国建设部.GB 50003—2001,砌体结构设计规范[S].北京:中国建筑工业出版社,2002.
[7] 杨卫忠.砌体受压本构关系模型[J].建筑结构,2008,38(10):80 ~82.
[8] 曹文文.砌体随机损伤本构关系的研究[D].郑州:郑州大学土木工程学院,2011.

