宽带多普勒声呐回波模型及特性研究

黄雄飞 苑秉成

（海军工程大学兵器工程系 武汉 430033）

，因此ki可以表示为τi的表达式，ki

，因此叠加噪声后的回波信

宽带多普勒声呐采用重复相位编码信号［1］和复协方差算法，相对于窄带技术大大提高了测量精度，并且已应用于多种载体的导航［2］．伪随机二相相位编码信号包括巴克码编码、M序列编码、L序列编码和互补编码等．伪随机二相相位编码信号具有较好的自相关特性，其模糊函数大都呈现近似图钉形，且频谱宽度较大，而重复伪随机二相相位编码信号同样具有较好的自相关特性和较大的频谱宽度，但与随机二相相位编码信形式不同，相关函数和频谱呈现多个峰值．海底回波模型和回波特性的研究对于波形设计和信号处理方法的研究具有重要的意义，因此本文建立了宽带多普勒声呐的回波模型，并分析了回波的相关特性和频谱特性．

1 发射信号特性

记重复二相伪随机码码元数为L，码元宽度为T0，重复次数为M，重复二相伪随机编码信号的复数形式［3］为

式中：a（t）为幅度调制函数，取二相伪随机编码信号的包络为矩形，幅度为单位幅度．即

Φ（t）为相位调制函数，只能取0或π两个值．重复二相伪随机编码信号的的功率谱［4］为

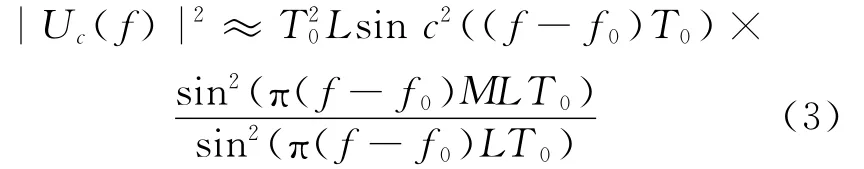
根据式（3），本文计算了码元为7位，重复5次，T0＝13．2μs，载波频率为300 k Hz，且经过移频的重复二相伪随机编码信号的频谱，如图1实线所示，虚线为同样信号幅度和信号长度的单频解析信号频谱．从图中可以明显看出二者的谱峰幅度和个数存在明显差异，重复二相伪随机编码信号的谱峰个数与码元数相等．谱峰的间隔为1／LT0，频谱最大值为MT0而单频解析信号的频谱最大值为MT0L，因此重复二相伪随机编码信号频谱最大值为单频解析信号频谱最大值的1／．同时，图1中的各谱峰宽度与同样信号长度的单频解析信号的谱峰宽度相等．

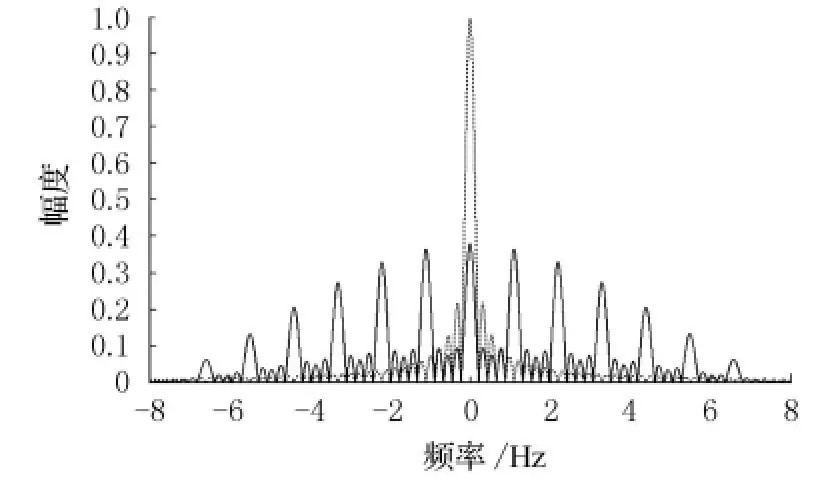
图1 重复二相相位编码信号频谱

2 海底回波信号模型

波束宽度为ψ的发射信号照射在海底波束照射海底所覆盖的区域，为一椭圆形．其中长轴a≈短轴为；Z为海底深度．见图2．

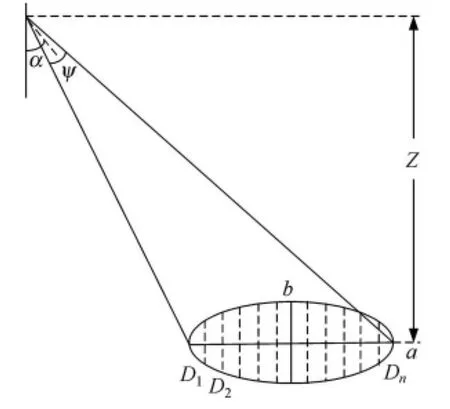
图2 多普勒声呐的波束照射示意图

波束最先照射到的区域为椭圆左侧，依次向右扩展，直到照射到整个椭圆，时间差为τ0＝式中：c为声速；一般情况下，α＝30°，ψ＝1～4°．将椭圆区域按照波束照射的时间先后划分为N个区域，标号分别为D1，D2，…，Dn，每块区域同换能器的连线与水平面的夹角为θi，每个划分的区域内包含了大量的散射单元．当N→∞时，D1，D2，…，Dn的厚度极小，因此可认为在此区域的所有散射单元距离换能器的距离相等，对应于每一个散射单元的回波信号［5］为

则ri（t）＝Ai×Δτ×s［ki（t－τi）＋φi］，i＝1，2，…，N．式中：A1，A2，…，An为对应散射区域回波信号的幅度，服从瑞利分布［6］；Δτ＝τN0；k为时间尺度压缩因子．上式表明，在回波信号中，不仅存在时延，信号在时间尺度上还受到压缩或拉伸，其中的尺度因子是．式中：c为水中声速；v为散射体相对运动的速度，以远离发射换能器为正，因此φ2，…，φn为回波的随机相位，服从均匀分布；τi＝，则换能器接收到的回波信号为

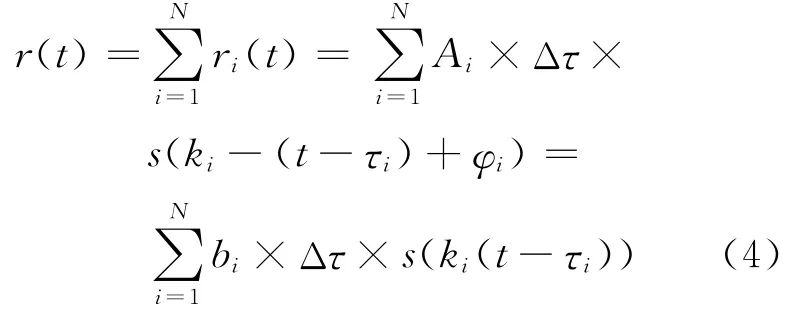
将θi表示成τi的表达式为cosθi＝号的连续表达式为

，因此ki可以表示为τi的表达式，ki

，因此叠加噪声后的回波信

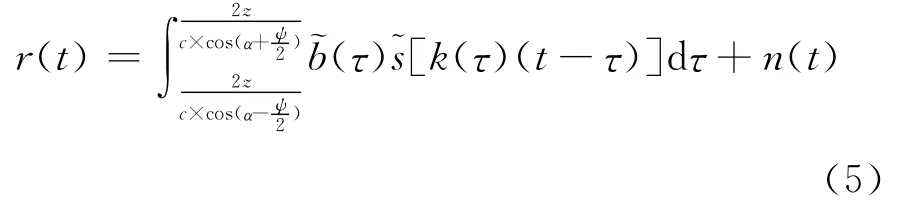
T，t4＝t2＋T，T为发射脉冲宽度．在t1＜t＜t2内为波束开始照射海底到完全照射海底的时间，t2＜t＜t3为波束完全照射海底的持续时间，t3＜t＜t4为波束完全照射海底到部分照射海底的时间．因此一般情况下，海底回波幅度是一个从小到大，然后又变小的过程．

3 海底回波的相关特性和谱分析

当2t0＋2τ0＜t＜2t0＋T－2τ0时，即仅考虑波束全部照射海底后的回波，回波的自相关函数为

R（x）＝ 〈r（t）r（t＋x）〉＝

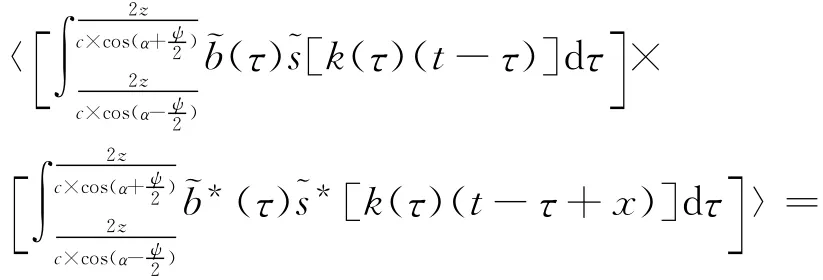
式中：Rs［k（τ）x］为发射信号的自相关函数，如图3所示，因此回波的自相关函数为具有不同压缩因子的单元散射信号自相关函数的叠加．令G（ω）为发射信号的功率谱，因此回波的功率谱为

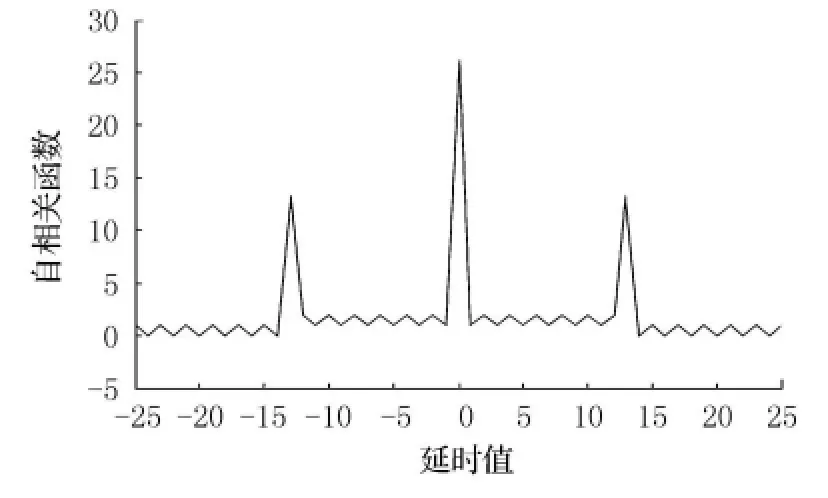
图3 重复二相相位编码信号自相关特性

从式（7）可以看出，回波功率谱形状与发射信号基本相同但是相对相对发射信号有一定的展宽，展宽大小约为［cos（α－）－cos（α＋）］＝sinαsin（），由于ψ＝1～4°因此回波功率谱展宽约为sinα×回波总带宽变为sinα×＋B．式中：B为发射信号的带宽．

因此宽带多普勒声呐的回波功率谱为

4 试验研究

以上建立的海底回波模型，分析了回波的相关特性和功率谱特性，下面从数字仿真和湖上试验的回波数据两个方面分析和验证宽带多普勒声呐的回波特性．

式（5）建立的是通用的海底回波模型，因此要分析宽带多普勒声呐的回波特性首先将式的重复二相相位编码信号代入式（5），得到宽带多普勒声呐的海底回波模型为

以一定的采样率fs采样回波信号，Ts＝1／fs，可得到回波的离散表达式为

取某次湖上实航试验的数据分析，试验条件为：波束宽度为4°，垂直波束倾角为20．7°，发射信号为重复相位编码信号，码元采用7位巴克码，重复次数为24次，发射脉冲宽度为11．2 ms，载波频率为150 k Hz，带宽15 k Hz，海底深度为19．5 m，因此经过计算得到τ0＝367μs，t1＝14．1 ms，t3＝24．9 ms，t4＝25．3 ms．图4为海底回波自相关的结果，从图中可见，回波自相关特性与理论分析完全一致，即回波的自相关与发射信号的自相关特性一致，相关峰的个数与发射信号一致，其位置由发射信号和径向速度共同决定．图5为根据式（10）的仿真海底回波自相关图，仿真条件与湖试试验一致，从图中可以看出，仿真回波的自相关特性与实际的海底回波特性一致，从而验证了本文所建立的海底回波模型的正确性．图6为海底回波的单边功率谱，功率谱估计采用韦尔奇方法［7］估计，由图可知，功率谱的形状和特性与理论分析一致，即回波功率谱与发射信号功率谱形状一致，回波功率谱呈梳齿状，谱峰的个数由发射信号参数决定即码元决定，谱峰间隔由码元宽度和码元长度决定，图7为根据式（10）的仿真海底回波功率谱图，仿真条件与湖试试验一致，从图中可以看出，仿真回波的功率谱与实际的海底回波特性一致，从而进一步验证了本文所建立的海底回波模型的正确性．

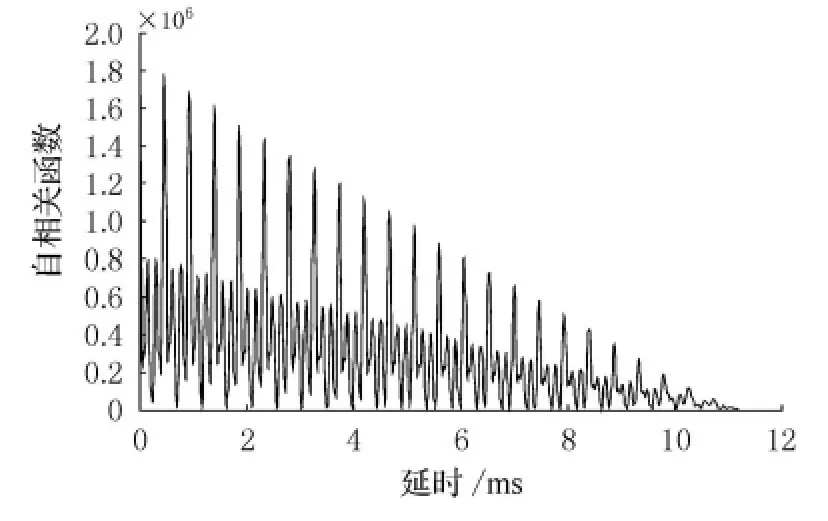
图4 海底回波自相关

图5 海底仿真回波自相关

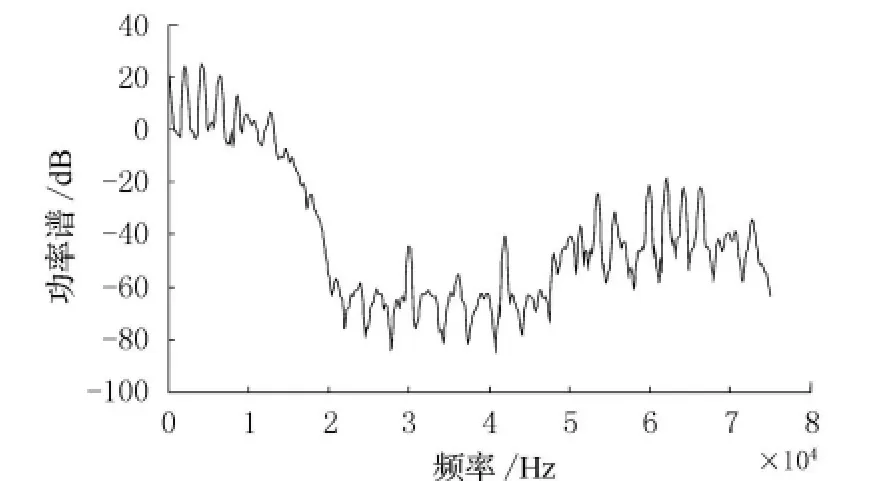
图6 海底回波功率谱

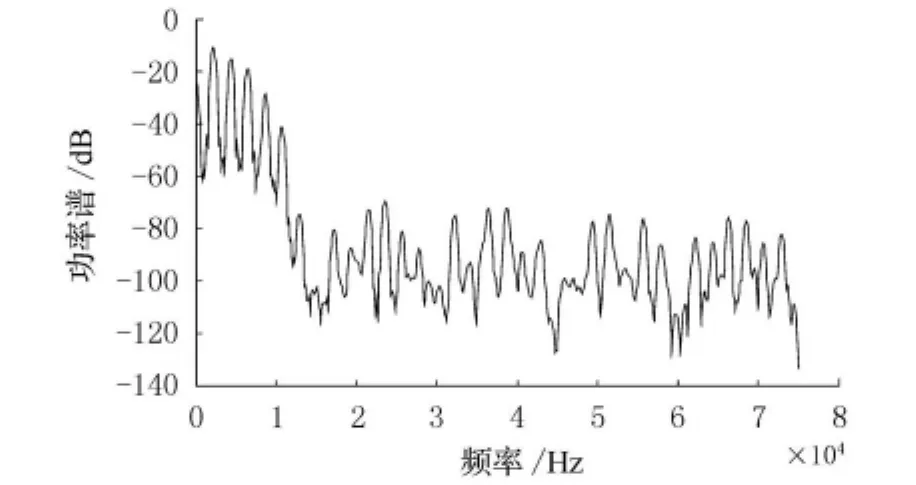
图7 仿真回波功率谱

5 结束语

本文对宽带多普勒声呐的发射信号及回波信号进行了研究．建立了海底回波模型，分析了回波的相关特性和功率谱特性，指出回波的相关值为具有不同压缩因子的单元散射信号自相关函数的叠加，功率谱回波功率谱形状与发射信号基本相同，但是相对相对发射信号有一定的展宽，最后根据建立的海底回波模型进行了数字仿真，得到了仿真回波的自相关图形和功率谱图形，同时分析湖上试验数据的自相关特性和功率谱特性，比较后发现二者具有较好的一致性．本文的分析和结论对于宽带多普勒声呐的系统分析和设计具有重要的意义．

［1］James C K，Louis L W．Toward in－situ calibration of gyro and doppler navigation sensors for precision underwater vechicle navigation［C］／／Proceedings of the 2002 IEEE International Conference on Robotics ＆Automation，Detroit，Washington D C，2002：399－406．

［2］Brumley．Broadband acoustic doppler current profiler：United States Patent Number，5，208，785［P］．May 4，1993．

［3］张明友，汪学刚．雷达系统［M］．2版．北京：电子工业出版社，2006．

［4］黄雄飞，苑秉成，陈 喜．宽带多普勒声呐信号频谱特性分析［J］．应用声学．2009，28（4）：278－282．

［5］惠俊英．水下声信道［M］．北京：国防工业出版社，1992．

［6］庄楚强，何春雄．应用数理统计基础［M］．广州：华南理工大学出版社，2000．

［7］陈亚勇．MATLAB信号处理详解［M］．北京：人民邮电出版社，2001．