飞机排班一体化模型与算法研究＊

高 强 朱星辉 李 云 朱金福

（南京航空航天大学民航学院 南京 210016）

0 引 言

广义的航班计划按照计划进行的先后顺序分为如下几个层次：（1）市场分析和航线的确立（包括城市之间旅客需求分析，每条航线航班频率的确定）；（2）航班时刻的编制（时刻表的设计）；（3）机型指派；（4）飞机排班（决定航班顺序，指定具体执行航班的飞机）（5）机组人员的排班．狭义的航班计划是指前3个层次，广义航班计划编制的步骤是按顺序完成的，没有任何反馈，实际操作管理中，航班计划的实施也是按顺序完成的．国外关于航班时间频率优化，机型指派的研究已经初具规模，飞机排班的研究主要集中在维护路线选择和机尾号指派［1－3］．现在，研究趋向于综合广义航班计划不同层次的计划，例如，机型指派可以综合航班时刻，飞机路线和机组计划．综合考虑有不同的方法．一种是完全一体化，一种是在各个步骤中反复进行［4－5］．

Ioachim［6］综合飞机指派和路线选择问题，同时考虑时间重排，提出了基于分支定界法的Dantzig－Wolfe分解寻找整数解．Desaulniers［7］使用Dantzig－Wolfe分解解决了日飞机路线选择和飞机指派问题．Sandhu和 Klabjan［8］将机型、路线和机组计划统一在同一个模型中．模型通过价值约束解决路线问题，这一点本质上意味着模型忽视了飞机路线的维修活动．并采用一种基于混合Lagrangian松弛与列生成算法和另一种Bender分解算法两种不同方法求解该问题，最后利用U．S航空公司数据进行了实例分析．

第二种一体化的方式是首先按照航班计划编制步骤顺序进行计划，通过后续计划对前面计划结果的反馈，重新调整方案，通常使用已经很成熟的模型，没有更深入的理论研究工作．国内关于广义航班计划一体化研究很不充分．飞机排班通常在机型指派的基础上，对同一种机型的航班进行路线选择和尾号指派．这样分步优化可以简化问题，降低求解难度，但基本不能得到全局最优解．同时，由于机型指派没有考虑飞机的运行约束，因此飞机排班可能无解．

为了改善分步优化的次优性，本文提出飞机排班一体化优化模型，同时对多机型的航班构建航班环，完成飞机指派工作．即机型指派，路线选择，尾号指派同时进行．该问题为大规模整数求解问题，是一个NP－Hard问题．本文提出一种改进的混合技术，即基于列生成算法的约束编程思想，采用混合约束编程（CP）和运筹学（OR）的技术求解飞机排班技术．即将CP算法嵌入到OR框架中，在基于约束编程的列生成算法中，主问题求解线性规划（OR），子问题通过CP列生成以求解困难约束，实现模型的高效求解．采用本方法还具有一个优势，可以识别航班计划的所需要的最小飞机架数与机型．当求解结束不存在可行解时，可逐步增加飞机数量直到求解结束得到可行解．当确定了最小飞机数量之后，可以变动飞机的机型以获得最低成本的机型配置．因此本方法对于航空公司中长期机队规划也具有一定的指导意义．

1 飞机排班一体化路径模型

针对国内航线网络和航班计划的特点，在航班时刻表确定，不考虑经停，只考虑飞机A检并且机场无容量限制的前提下，综合考虑机型指派、路线选择以及尾号指派，建立日飞机排班一体化0－1整数规划模型，给出指派结果以及飞机路线．本模型基于飞机路线D:xmlJTKJ15106591JTKJ15106591 杨艳红 （已改），即对于具体一架飞机，首先构建满足航班衔接、维护、预指派等要求的一天航班环，然后综合考虑航空公司飞机等资源限制，以成本最小为目标建立模型．

式中：F为航班集合，f∈F，每个航班信息包括出发时间（f．dep T），到达时间（f．arr T），出发机场（f．dep A），到达机场（f．arr T），预测旅客量（f．pax）和平均票价（i．price）；A 为飞机集合，a∈A；K 为所有机型集合，∀a∈A，k（a）∈K，k（a）为飞机a的机型．机型包括最小过站时间（k．turnround）；基地机场b（k），可以是单维修基地或者多维修基地；机型座位数（k．S）；日最大起降 次 数 （k．Max duty）；机 型 单 位 运 行 成 本（k．cost）．B 为所有基地机场的集合，∀a∈A，b（k（a））∈B；L 为所有满足要求的飞机路线集合．a∈A，La表示所有由飞机a执行的飞机路线集合，l∈La⊆L．按照f．dep T 对航班排序，即ordered by dep T，low（l）为飞机路线l的首航班，up（l）为飞机路线l的尾航班．Pa为预先指定必须由飞机a执行的航班集合，即预指派；Ra为预先指定不能由飞机a执行的航班集合，即航班限制．CL为执行该飞机路线的成本，包括该飞机执行所有航班的运行成本clope和旅客溢出（座位数少于旅客数）成本cslpi．这里，clope为机型单位运行成本与飞机路线上所有航班总飞行时间的乘积，为所有航班旅客溢出成本之和．afl：示性算子

bal：示性算子飞机a执行飞机路线l飞机a不执行飞机路线l xj：0－1型决策变量，

式（1）为成本最小化目标函数．式（2）为覆盖约束，要求每个航班指派一架飞机且只有一架，如果允许加班，可放宽约束．式（3）为飞机数目约束，一架尾号的飞机只能执行一条路线，要求所需飞机架数不超过可用飞机数．式（4）与（5）为航班限制约束．式（6）为资源约束，指一种机型执行的航班总数不能超过最大值．式（7）为对于每架飞机的路线合法性要求，满足航班机场衔接，最小过站时间要求，飞机路线首航班从基地出发，尾航班到达机场与首航班出发机场一致，满足日维修要求，同时使次日有同样的飞机分布．

除了上述连接约束、维修和航班限制，航空公司实际运营中还有一些别的约束，比如保证飞机路线与机组匹配，规定飞机转场时间满足机组换班时间要求．此外，飞机均衡使用要求也是常见的．有时，某些特定机场会限制着陆次数，飞行时间，飞行工作日等，这些要求都可以通过累积约束建模．数学规划中，这些约束称为资源约束．

2 基于约束编程的列生成算法

由路径模型看出，飞机排班一体化主要有两类约束：

1）对具体一条飞机路线的约束．包括预指派（4），航班限制约束（5）以及最大起飞架次（6），航班衔接及维修基地约束（7），约束中的参数只与所用飞机及其机型相关，称CP约束．

2）对通解的约束．包括航班覆盖约束（2）和飞机总资源约束（3），称为LP约束．

2．1 主问题（master problem，MP）

根据列生成的特点，主问题是根据LP约束求解整数规划，根据路径模型得到主问题

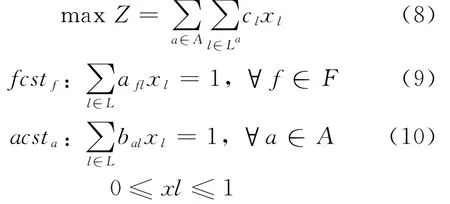
ILOG的OPL语言支持约束声明，如：Constraint fcstf，acsta；表示分别声明约束数组fcst和acst，∂f是与航班f相关约束的对偶值，βa是与飞机a相关约束的对偶值．求解MP，返回每个约束的对偶值，即

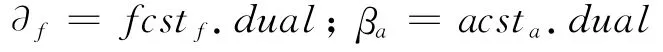
以中型航空公司日航班计划为例，满足CP约束的列（飞机路线）的数目也是巨大的，所以这里采用动态列生成算法，即LP中只使用飞机路线的子集，如果这些路线集合是一体化模型的可行解，主问题为限制主问题（RMP）．

2．2 基于约束编程的子问题（Subproblem，SP）

根据飞机排班的特点，列生成算法中的列定义为飞机路线，即由某架飞机执行一系列航班的集合，满足航班时刻表、维修约束、预指派、航班限制等CP约束．根据列生成的简约成本更新路线子集．列l的简约成本rcl和负简约成本NRCl为

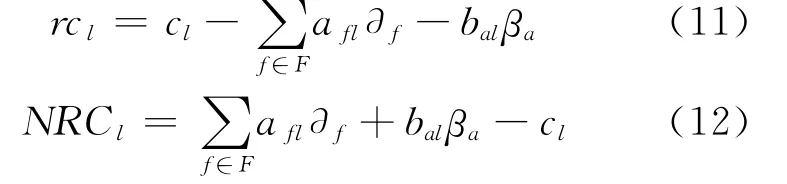
使用约束编程生成可能的路线．约束编程（constraint programming，CP）能高效实现飞机排班的列生成算法：（1）搜索策略：本文使用CP求解器为ILOG Solver，提供约束语言描述问题的变量、约束条件以及默认的搜索算法（深度优先、广度优先），可根据需要自己定义控制搜索策略．（2）约束传播：也称信息传播．ILOG平台能够在搜索过程中，集中利用约束，计算并传播每个决策点的结果，及时检测，删除不可能出现在最终解的变量赋值．与传统搜索相比，可以有效的域缩减，减少回溯次数．搜索和传播通常是结合使用，相辅相成的．

1）最优路线 即最优列，指当前列集L中具有最大负简约成本的列，单机型问题中是资源约束最短路，多机型中可以认为最小费用流问题，根据主问题得到最优路线的目标函数为

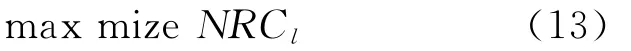
根据CP约束中航班衔接约束，构建约束传播算法：

算法1 约束传播

路线生成中，同时使用集合变量．如集合flt Rng，是一条路线中航班顺序集合，flt Rng［i］是路线中第i个航班．同样citySeq路线中依次经由机场集合．citySeq［0］是出发基地机场．根据上界和下界确定集合变量的当前域，称为指定集req（flt Rng）和可能集pos（flt Rng），集合变量的值是req（fltRng）的超集，pos（flt Rng）的子集．初始，pos（flt Rng）包含所有的航班，req（flt Rng）为空，在路线生成的时候，约束传播和搜索策略不断删除可能集中的航班，增加指定集中的航班．一旦两集合相等，得到一个集合变量的值．例如，初始pos（fit Rng）含有4个航班，f1，f2，f3，f4，满足性质

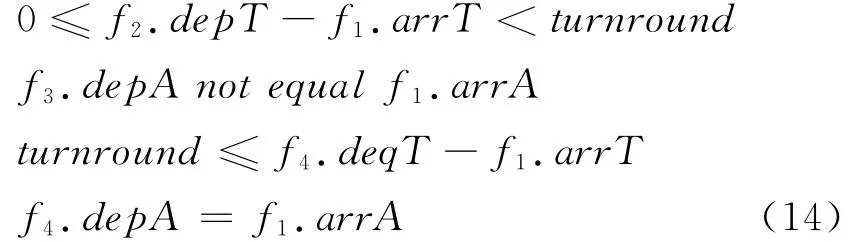
f1加入req（flt Rng），f2与f1不满足最小过站时间，将f2从pos（fltRng）中删除．此时f1后航班为f3，不满足机场衔接，将f3从pos（flt Rng）中删除．f4与f1满足时间和机场衔接要求，将其加入req（flt Rng）．最后得到集合变量flt Rng的值为：flt Rng［0］＝f1；flt Rng［1］＝f4．域缩减变化见表1．

表1 域缩减

同样，利用约束编程表述维修基地约束、预指派航班限制约束、最大起飞架次约束，好的约束描述能够起到加快传播的作用．另外可以结合使用搜索策略．

算法2 搜索策略

针对目标函数求最大负简约成本的特点，首先根据对偶值∂f对航班排序，利用ILOG内置深度搜索，确定选择点（choice），然后通过约束传播约束以及其他CP约束对选择点判断．直至完成搜索．得到最优路线，返回最优路线的目标值为

2）更新列集 利用当前列集获得的最优路线的负简约成本，生成满足一定条件的列集更新L，减少迭代次数．比如要求新生成列满足

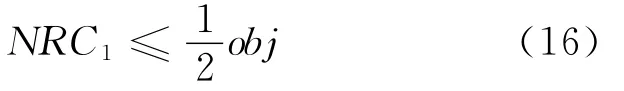
约束表述中涵盖了所有针对单个飞机所有的路径约束，即CP约束．此时搜索策略为ILOG生成指令，为一架飞机生成执行的航班集合

一旦新列满足CP约束并且满足式（16），将其加入L集合中，返回限制主问题，重新求解线性规划．反复进行，直至没有新列加入．如果无法继续生成负简约成本的列的时候，生成算法结束，此时得到整数规划主问题最优解．

3 算例分析

某航空公司有2种机型，6架飞机，日执行31个航班，2个维修基地机场．基中航班F28为跨海航班，必须由飞机A0001执行．航班信息表见表2．机型数据见表3．分阶段排班结果与一体化排班结果见表4．

在ILOG＿studio中编写OPL程序，输入航班、机型、飞机数据，编译各功能模型，运行scrip脚本语言控制模型之间的数据交换，并输出最优飞机路线集．首先生成初始列3 168条，在迭代过程中负简约成本飞机数量不断变化，其变化趋势如图1．LP中列数目随主问题迭代的变化趋势如图2．最终生成5 890列．经过测试，静态列生成得到的14 778列，对比可知，基于约束编程的动态列生成大大减少了列规模．

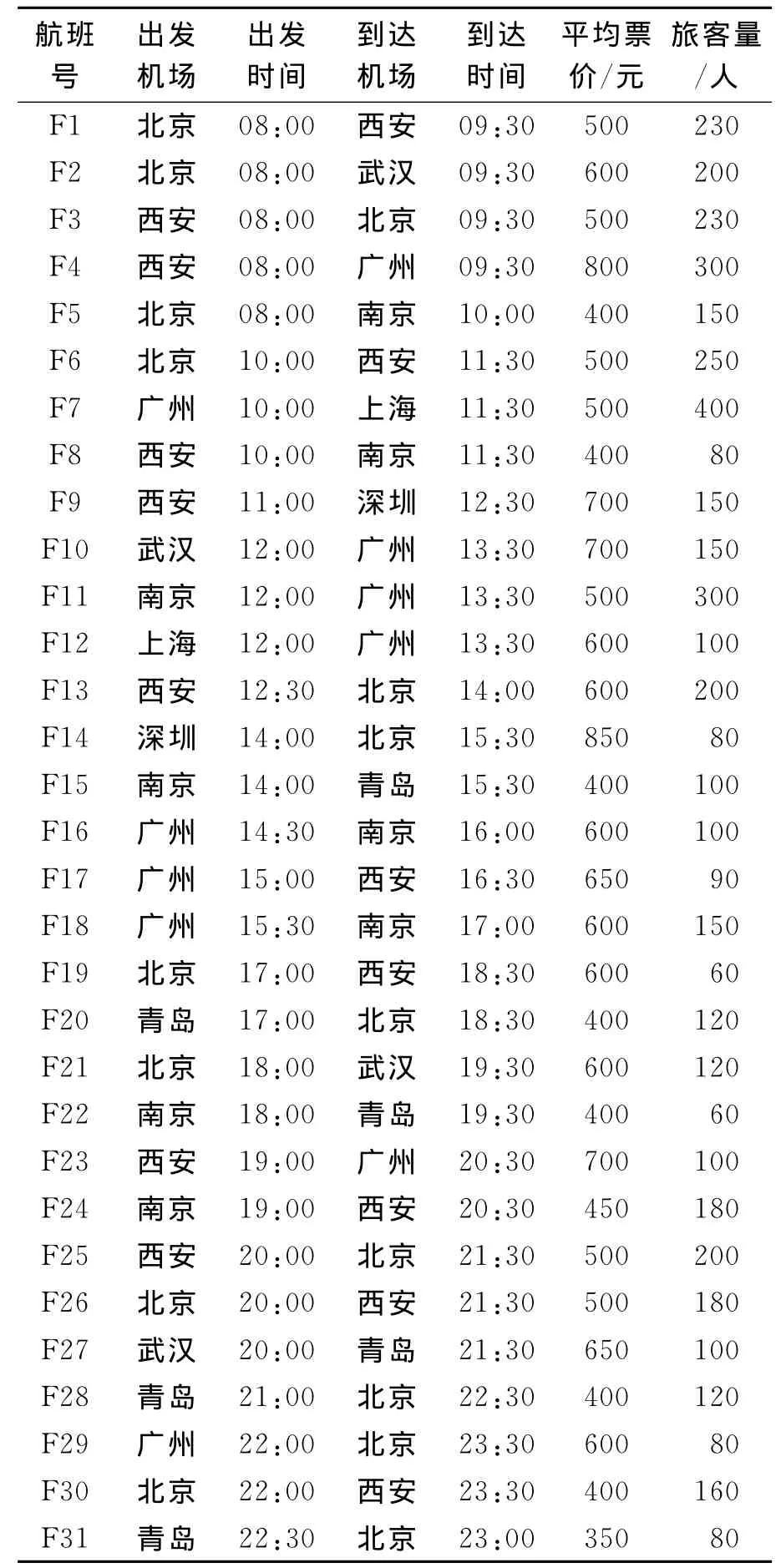
表2 航班数据表

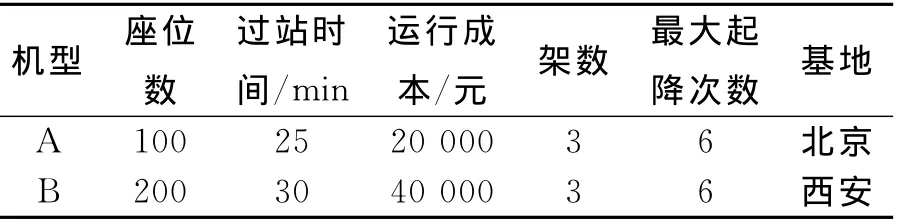
表3 各机型数据表

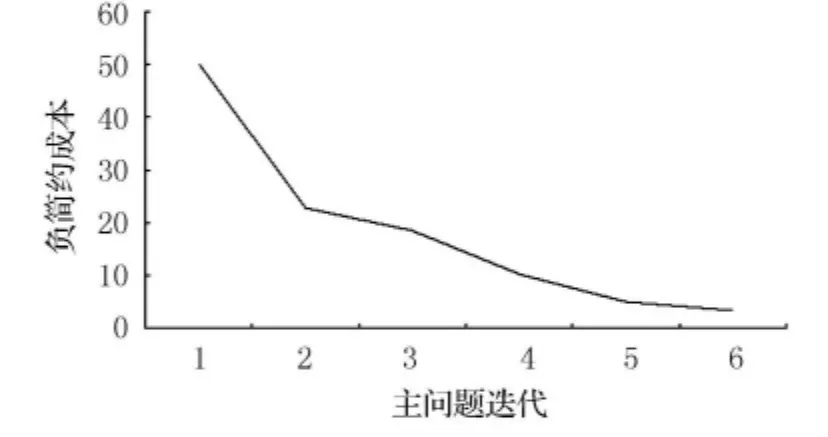
图1 负简约成本飞机路线随主问题迭代的变化趋势

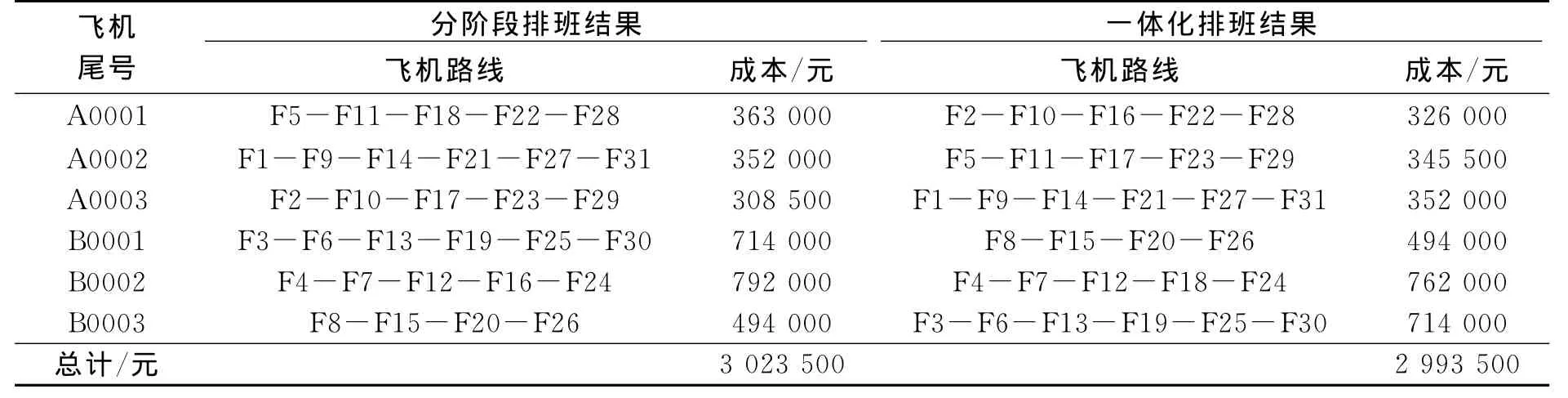
表4 分阶段排班与一体化排班比较

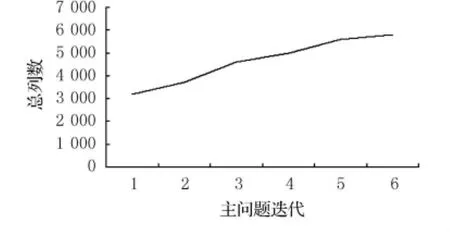
图2 总列数随主问题迭代的变化趋势

运行结果给出最优的6架飞机对应的飞机路线，最小成本为2 993 500元，比航空公司分阶段排班结果成本降低约1%．运行时间为314．556 s（CPU：PM4，2．66 G，内存512 M）．

4 结束语

针对航班计划顺序计划次优性，提出综合考虑机型指派，维护路线选择，飞机指派等因素的飞机排班一体化模型，并利用混合约束编程和列生成算法技术求解．实现航班计划的自动化，保证全局最优性．在ILOG平台上编写程序，利用实际数据测试验证模型算法．可以看出，与传统的列生成相比，约束编程可以简单清楚的表达现实中的约束，系统易于维护，同时约束传播和搜索策略可以显著改善列生成的效率．

［1］Hane C A，Barnhart C．The fleet assignment problem［J］．Interfaces，1989，19（4）：20－28．

［2］Lloyd C．The aircraft rotation problem［J］．Annals of Operations Research，1997，69：34－35．

［3］Talluri K T．The four－day aircraft maintenance routing problem［J］．Thransportation Science，1998，31（1）：43－48．

［4］屈 援，汪 波，钟石泉．单车场集送一体化车辆路径问题及其混合算法研究［J］．武汉理工大学学报：交通科学与工程版，2007，31（5）：811－814．

［5］张 煜，李文锋，严新平．集装箱作业系统一体化调度研究综述［J］．武汉理工大学学报：交通科学与工程版，2011，35（1）：11－14．

［6］Ioachim I，Desrosiers J，Soumis F，et al．Fleet assignment and routing with schedule synchronization constraints［J］．European Journal of Operational Research，1999，119（1）：75－90．

［7］Desaulniers J，Desrosiers J，Dumas Y，et al．Daily aircraft routing and scheduling［J］．Management Science，1997，43（6）：841－855．

［8］Sandhu R，Klabjan D．Integrated airline fleeting and crew－pairing decisions［J］．Operations Research，2007，55（3）：439－456．