城际公交车高峰时段发车间隔时间优化

曲思源 徐行方 洪 玲

（同济大学交通运输工程学院1） 上海 201804） （上海铁路局调度所2） 上海 200071）

公交车辆发车时刻表是公共交通管理系统中重要的计划表，是调度员工作以及车辆正常运行的最基本依据．编制车辆发车时刻表最关键的问题就是确定发车间隔．伴随着我国城际铁路的发展，“大运量、小编组、高密度、公交化”的运营模式营模式使得城际铁路在城际客运通道中客流分担率逐渐上升．为确保城际公交车客流分担率保持平稳或上升，同时满足旅客出行需要，城际公交车发车间隔应当按照“以人为本”的原则，以较高的行车密度、较少的旅客候车时间，实现旅客方便、便捷、快速地出行，即旅客在一定的时间范围内，几乎不受车辆到发时刻限制，可随到随走，并以较短的旅行时间到达目的地．一般说来，城际公交车发车间隔要根据不同时间内乘客需求的变化来制定不同时段的发车间隔时间，可将时段划分为早高峰、平峰和晚高峰3个不同时段，特别是高峰时段，其开行车次的间隔时间优化是衡量城际公交运营质量重要的参数．在研究发车间隔方面，已有文献多是在发车间隔均等的前提下展开研究的，如文献［1］将车辆出行费用描述为计划延误费用和车内费用两部分，以旅客出行费用和铁路成本费用最小化为目标建立了优化模型并进行了分析求解．文献［2］建立了理想状态下的城际轨道交通旅客候车时间总和数学期望最小的多目标规划模型．本文将旅客到达城际公交站发站的过程视为随机过程，模拟旅客提前到站候车时，根据公交车不同停站类型有多辆车选择乘坐的实际，建立起不均等的公交车开行间隔时间优化模型和相应旅客候车等待时间的数学模型，以便为城际公交运营组织的优化提供借鉴．

1 泊松过程

定义1 若｛N（t），t∈［0，＋∞）］为一计数过程，当满足如下条件：N（0）＝0；对于任意的s≥t≥0，Δt＞0，增量N（s＋Δt）－N（t＋Δt）与 N（s）－N（t）具有相同的分布函数；对于任意的正整数n，任意的非负实数0≤t0≤t1≤…≤tn，增量N（t1）－N（t0），N （t2）－N （t1），…，N （tn）－N（tn－1）相互独立；对于足够小的 Δt，有

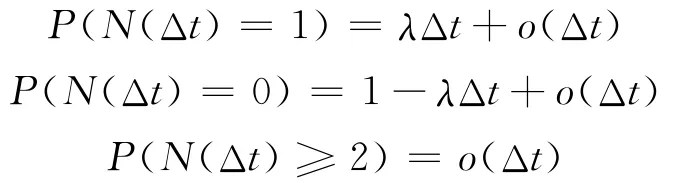
则称｛N（t），t∈［0，＋∞）］是强度为λ的泊松过程，其数学期望

引理1 设｛N（t），t≥0｝是一泊松过程，N（t）表示［0，t）内质点出现的个数，以τn表示第n 个质点的到达时刻，n＝1，2，…，其累计分布函数和概率密度分别为［3］

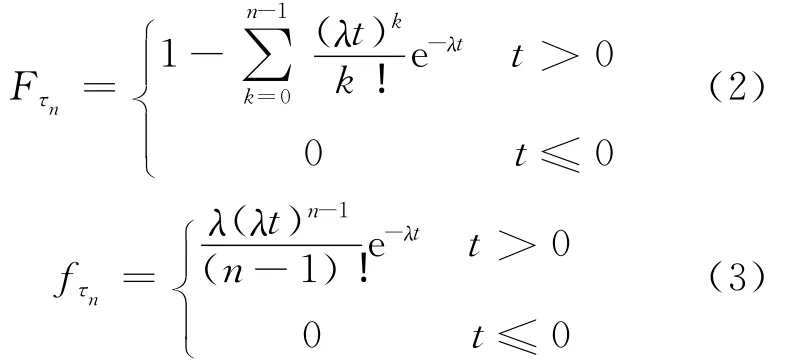
引理2 设｛N（t），t≥0｝在［0，t）时段内进入含有n个子系统L的随机质点个数，每个质点独立地以概率Pj，（j＝1，2，…，m； ＝1）进入L的第j个子系统，用Nj（t）表示在［0，t）时段内进入第j个子系统的随机质点个数，若N（t）服从强度为λ的泊松过程，则N（t）＝ （t），｛Nj（t）相 互 独 立；j ＝ 1，2，…，m｝，且 固 定t，｛Nj（t）｝是强度为λPj的泊松过程．

引理3 设｛N（t），t≥0｝是强度为λ的泊松过程，对于任意的实数t＞0，若N（t）＝n＞0，则该过程的前n个质点发生的时刻（τ1，τ2，…，τn）和n个在［0，t］上均匀分布的相互独立的随机变量（U1，U2，…，Un）的次序统计量有相同的n维联合分布［4］．

2 模型建立

2．1 公交车开行间隔时间模型

根据大量的数据调查可知，有60%的旅客愿意提前30～60 min到达始发站．定义旅客候车时间是指旅客到公交始发站候车时起至乘坐某一辆车次出发时止的整个过程．某同一方向，旅客一般按照车次时刻表提前到站候车，且有不同停站方案的多辆车次可供选择．针对旅客候车的实际，模拟同一去向的旅客在［0，t］内陆续到达始发站，该始发站安排Aj（1≤j≤m）辆供旅客选择，设到达该始发站的旅客数N（t）是一服从强度λ的泊松过程，每个旅客进入Aj辆车的概率分别为pj（j＝1，2，…，m ＝1），用 Nj（t）表示在［0，t）时段内进入第Aj辆的随机旅客数，根据引理2可知N（t）＝ （t），｛Nj（t）相互独立；j＝1，2，…，m｝，并且｛Nj（t）｝是强度为λPj的泊松过程．以τn，j表示Aj辆车第n个旅客的到达时刻，n＝1，2，…，则累计分布函数和概率密度分别为

假设当旅客到达数为n时，该辆便发车，即第n位旅客到达的数学期望为该次车辆等待时间的数学期望

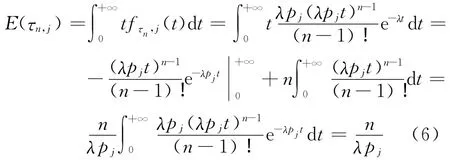
令Aj辆发车的时间为tj，有

则合理的车辆间隔为

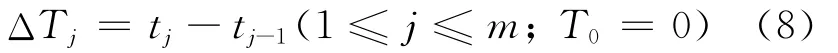
根据分布函数的定义，有Fτn，j（t）＝P（τn，j≤t），注意到｛τn，j≤t｝表示第n个旅客在时刻t之前出现，这就意味着在［0，t）内至少到达了n个旅客，于是有

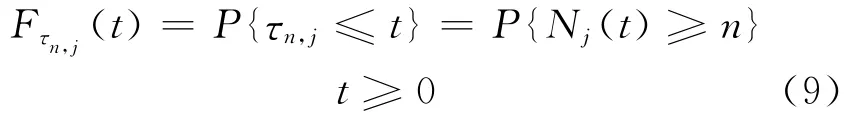
若令n表示定员时，理论上可用Fτn，j表示Aj辆的上座率，根据式（4）、（7）可分别求得每辆的上座率ρj．

2．2 旅客等候时间模型

设［0，t）时段内进入 Aj辆车旅客数Nj（t），设第i个旅客到达车站的时刻为Wji，则在［o，t］到达车站的旅客等待Aj时间总和为［5－7］

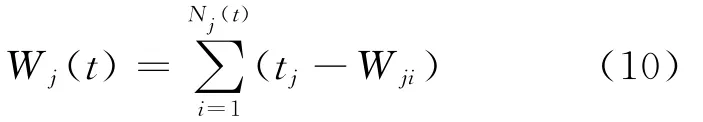
因为

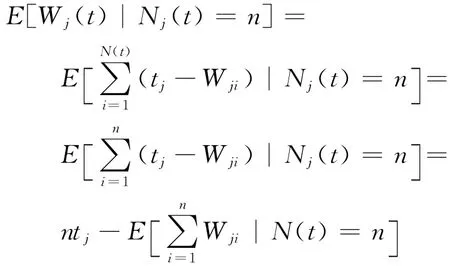
记｛Yi，1≤i≤n｝为［0，t］上独立同均匀分布的随机变量，Y（1）≤Y（2）≤…≤Y（3）为相应的顺序统计量．由引理3，存在

因此

所以

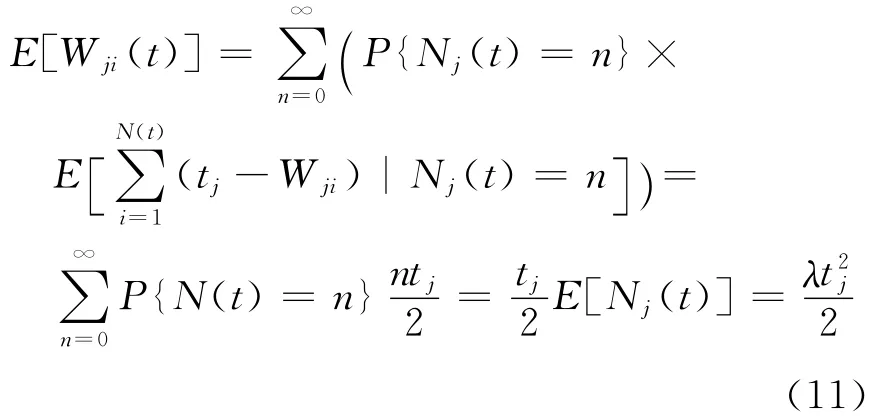
3 算例分析

某一城际公交站早高峰时段内，允许最小开行间隔时间为5 min，采用同一型号车，每车定员为50人，在某一高峰时段内，拟安排4种类型，以沿线所设站为衡量标准，即一站直达A、跨线运行（三站起停）B、快车（二站起停）C和慢车（站站停）D四种类型，同一去向的旅客到达车站服从泊松过程，其到达强度λ＝50人／min，准备安排9辆车该时段始发，始发顺序为1～9（车次代号），通过客流调查，旅客进入每辆车的概率分别为

求合理的始发间隔时间和旅客候车等待每次辆车的平均等待时间总和．

根据式（1）、（8）、（11），可计算各车次间隔时间计算表，见表1．

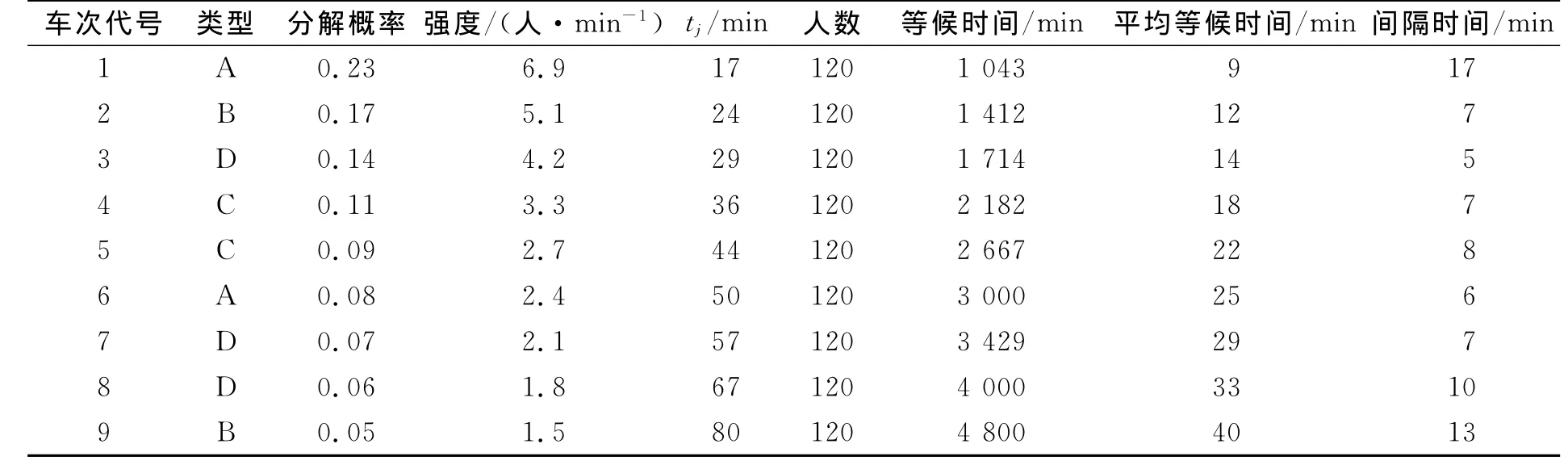
表1 各车次间隔时间计算表

显见，在［0，80］的时间时段内，可分别求得各车辆在该始发站发车不均等的间隔时间，其中第4辆和第3辆采取追踪运行模式，即两辆车间隔时间仅为5 min，该模型能为采取公交车辆追踪开行方式的原因提供理论依据．同时，也能验证，若分解概率越低，各车次发车间隔时间将越长．

4 结束语

城际公交始发站发车间隔时间是基于公交化运营模式，据旅客到达强度，采用随理论求得的不确定模型．考虑到每一时段旅客到达车站强度分配各次辆车的强度值是模型优化的必要条件，因此需要深入进行客流调查，以便取得准确的数值．辆车开行不均等间隔时间模型同时能为辆车开行方案的优化提供了新的思路．城际公交车发车间隔除根据乘客需求、车型定员、满载率外，还要依据行驶速度、停站安排和时间、线路通行能力、交通流量等因素综合确定，其车辆间隔时间优化有待进一步分析．

［1］秦 进，史 峰．公交化城际辆车的最优时刻表研究［EB／OL］．［2011－10－11］中国科技论文在线．http：／／www．paper．edu．cn．

［2］廖 勇．公交化城际列车开行间隔优化［J］．铁道学报，2010，32（1）：8－12．

［3］李裕奇．随机过程［M］．北京：国防工业出版社，2003．

［4］王志刚．应用随机过程［M］．合肥：中国科学技术大学出版社，2009．

［5］肖龙文，史 峰．铁路公交化旅客列车开行方案优化［J］．湖南大学学报：自然科学版，2009（1）：55－58．

［6］谢如鹤，宗 岩，王荣华，等．城际铁路客运公交化的综合评价［J］．广州大学学报：自然科学版，2005（1）：78－82．

［7］许焕卫，黄洪钟，张 旭．基于模糊折中规划的稳健多目标优化设计［J］．大连理工大学学报，2007（3）：56－60．